ME-Net: A Multi-Scale Erosion Network for Crisp Building Edge Detection from Very High Resolution Remote Sensing Imagery
Abstract
:1. Introduction
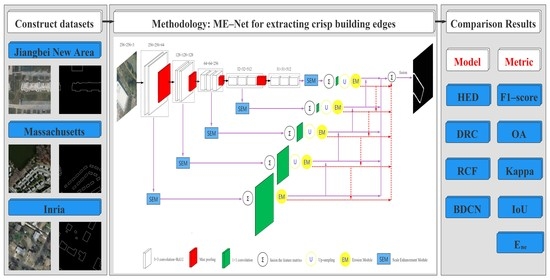
- We constructed the Jiangbei New Area building edge dataset and reconstructed two building edge datasets based on the public Massachusetts and Inria building region datasets; We then re-trained and evaluated the state-of-the-art DCNNs-based edge detection networks (HED, DRC, RCF, and BDCN) on the three large building edge datasets of very high resolution remote sensing imagery;
- Based on the architecture of BDCN, a multi-scale erosion network (ME-Net) was proposed to detect crisp and clear building edges by designing an erosion module (EM) and a new loss function. Compared with the state-of-the-art networks on each dataset, the results demonstrated the universality of the proposed network for building edge extraction tasks;
- We proposed a new metric of non-edge energy (Ene) to measure the non-edge noise and thick edge, and the metric has shown reliability by exhaustive experiments and visualization results of crisp edges.
2. Dataset Construction
2.1. Jiangbei New Area Building Dataset
- (1)
- The manually vectorized building edge maps were converted to raster binary label images;
- (2)
- To avoid memory overflow caused by large images, the original aerial images and label images were cropped into patches of 256 × 256 pixels;
- (3)
- The patches containing buildings were augmented by rotating them 90°, 180°, and 270°.
2.2. Massachusetts Building Dataset
2.3. Inria Building Dataset
3. Methodology
3.1. Architecture Overview
3.2. Erosion Module
3.3. The Proposed Loss Function for Crisp Edge Detection
3.4. Evaluation Metrics
3.5. The Proposed Ene for Edge Crispness Measuring
4. Experiments and Results
4.1. Training Details
4.2. Comparison Experiments
4.2.1. Results on Jiangbei New Area Dataset
4.2.2. Results on Massachusetts Dataset
4.2.3. Results on Inria Dataset
5. Discussion
5.1. Reliability Verification of Codes
5.2. Comparative Analysis with Segmentation Methods
5.3. Ablation Analysis and Cross-Dataset Evaluation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, S.; Luo, L.; Cao, K.; Shu, M. Extracting building patterns with multilevel graph partition and building grouping. ISPRS J. Photogramm. Remote Sens. 2016, 122, 81–96. [Google Scholar] [CrossRef]
- Siddiqui, F.U.; Teng, S.W.; Awrangjeb, M.; Lu, G. A robust gradient based method for building extraction from LiDAR and photogrammetric imagery. Sensors 2016, 16, 1110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, G.; Guo, Z.; Shi, X.; Chen, Q.; Xu, Y.; Shibasaki, R.; Shao, X. A boundary regulated network for accurate roof segmentation and outline extraction. Remote Sens. 2018, 10, 1195. [Google Scholar] [CrossRef] [Green Version]
- Zhao, K.; Kang, J.; Jung, J.; Sohn, G. Building extraction from satellite images using mask R-CNN with building boundary regularization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 247–251. [Google Scholar] [CrossRef]
- Xia, G.; Huang, J.; Xue, N.; Lu, Q.; Zhu, X. GeoSay: A geometric saliency for extracting buildings in remote sensing images. Comput. Vis. Image Underst. 2019, 186, 37–47. [Google Scholar] [CrossRef] [Green Version]
- Zorzi, S.; Fraundorfer, F. Regularization of Building Boundaries in Satellite Images Using Adversarial and Regularized Losses. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5140–5143. [Google Scholar] [CrossRef]
- Lu, N.; Chen, C.; Shi, W.; Zhang, J.; Ma, J. Weakly supervised change detection based on edge mapping and SDAE network in high-resolution remote sensing images. Remote Sens. 2020, 12, 3907. [Google Scholar] [CrossRef]
- Liu, H.; Luo, J.; Huang, B.; Hu, X.; Sun, Y.; Yang, Y.; Xu, N.; Zhou, N. DE-Net: Deep encoding network for building extraction from high-resolution remote sensing imagery. Remote Sens. 2019, 11, 2380. [Google Scholar] [CrossRef] [Green Version]
- Kang, W.; Xiang, Y.; Wang, F.; You, H. EU-net: An efficient fully convolutional network for building extraction from optical remote sensing images. Remote Sens. 2019, 11, 2813. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.; Fu, Y.; Gan, M.; Deng, J.; Comber, A.; Wang, K. Building extraction from very high resolution aerial imagery using joint attention deep neural network. Remote Sens. 2019, 11, 2970. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Gong, W.; Sun, J.; Li, W. Web-net: A novel nest networks with ultra-hierarchical sampling for building extraction from aerial imageries. Remote Sens. 2019, 11, 1897. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Yao, X.; Fang, Y. Building-a-nets: Robust building extraction from high-resolution remote sensing images with adversarial networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3680–3687. [Google Scholar] [CrossRef]
- Cheng, M.-M.; Zhang, Z.; Lin, W.-Y.; Torr, P. BING: Binarized Normed Gradients for Objectness Estimation at 300fps. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3286–3293. [Google Scholar] [CrossRef] [Green Version]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. From contours to regions: An empirical evaluation. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2294–2301. [Google Scholar] [CrossRef] [Green Version]
- Kittler, J. On the accuracy of the Sobel edge detector. Image Vis. Comput. 1983, 1, 37–42. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. 2010, 33, 898–916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, J.J.; Zitnick, C.L.; Dollar, P. Sketch Tokens: A Learned Mid-level Representation for Contour and Object Detection. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3158–3165. [Google Scholar] [CrossRef]
- Dollar, P.; Tu, Z.; Belongie, S. Supervised Learning of Edges and Object Boundaries. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition—Volume 2 (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 1964–1971. [Google Scholar] [CrossRef]
- Dollár, P.; Zitnick, C.L. Fast edge detection using structured forests. IEEE Trans. Pattern Anal. 2014, 37, 1558–1570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ganin, Y.; Lempitsky, V. N4-fields: Neural network nearest neighbor fields for image transforms. In Asian Comference on Computer Vision (ACCV); Springer: Cham, Switzerland, 2014; pp. 536–551. [Google Scholar] [CrossRef] [Green Version]
- Shen, W.; Wang, X.; Wang, Y.; Bai, X.; Zhang, Z. DeepContour: A deep convolutional feature learned by positive-sharing loss for contour detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3982–3991. [Google Scholar] [CrossRef]
- Bertasius, G.; Shi, J.; Torresani, L. DeepEdge: A multi-scale bifurcated deep network for top-down contour detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4380–4389. [Google Scholar] [CrossRef] [Green Version]
- Hwang, J.; Liu, T. Pixel-wise deep learning for contour detection. arXiv 2015, arXiv:1504.01989. [Google Scholar]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote Sens. Lett. 2017, 8, 136–145. [Google Scholar] [CrossRef]
- Luus, F.P.; Salmon, B.P.; Van den Bergh, F.; Maharaj, B.T.J. Multiview deep learning for land-use classification. IEEE Geosci. Remote Sens. 2015, 12, 2448–2452. [Google Scholar] [CrossRef] [Green Version]
- Nogueira, K.; Penatti, O.A.; Dos Santos, J.A. Towards better exploiting convolutional neural networks for remote sensing scene classification. Pattern Recogn. 2017, 61, 539–556. [Google Scholar] [CrossRef] [Green Version]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. 2015, 13, 105–109. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Xiang, S.; Liu, C.; Pan, C. Vehicle detection in satellite images by hybrid deep convolutional neural networks. IEEE Geosci. Remote Sens. 2014, 11, 1797–1801. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, Z.; Wu, J. A hierarchical oil tank detector with deep surrounding features for high-resolution optical satellite imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4895–4909. [Google Scholar] [CrossRef]
- Ševo, I.; Avramović, A. Convolutional neural network based automatic object detection on aerial images. IEEE Geosci. Remote Sens. 2016, 13, 740–744. [Google Scholar] [CrossRef]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. Learning low dimensional convolutional neural networks for high-resolution remote sensing image retrieval. Remote Sens. 2017, 9, 489. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE international conference on computer vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Cheng, M.-M.; Hu, X.; Wang, K.; Bai, X. Richer Convolutional Features for Edge Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3000–3009. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhao, X.; Li, Y.; Huang, K. Deep crisp boundaries: From boundaries to higher-level tasks. IEEE Trans. Image Process. 2018, 28, 1285–1298. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Zhang, S.; Yang, M.; Shan, Y.; Huang, T. Bi-Directional Cascade Network for Perceptual Edge Detection. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3828–3837. [Google Scholar] [CrossRef] [Green Version]
- Poma, X.S.; Riba, E.; Sappa, A. Dense extreme inception network: Towards a robust cnn model for edge detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 1923–1932. [Google Scholar]
- Cao, Y.; Lin, C.; Li, Y. Learning crisp boundaries using deep refinement network and adaptive weighting loss. IEEE T. Multimedia. 2020, 23, 761–771. [Google Scholar] [CrossRef]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using brightness and texture. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–13 December 2003; pp. 1279–1286. [Google Scholar]
- Lu, T.; Ming, D.; Lin, X.; Hong, Z.; Bai, X.; Fang, J. Detecting building edges from high spatial resolution remote sensing imagery using richer convolution features network. Remote Sens. 2018, 10, 1496. [Google Scholar] [CrossRef] [Green Version]
- Deng, R.; Shen, C.; Liu, S.; Wang, H.; Liu, X. Learning to predict crisp boundaries. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 562–578. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Mnih, V. Machine Learning for Aerial Image Labeling; University of Toronto: Toronto, ON, Canada, 2013. [Google Scholar]
- Zhang, Z.; Wang, Y. JointNet: A common neural network for road and building extraction. Remote Sens. 2019, 11, 696. [Google Scholar] [CrossRef] [Green Version]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Can semantic labeling methods generalize to any city? In the inria aerial image labeling benchmark. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3226–3229. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Zhu, X.X. RiFCN: Recurrent network in fully convolutional network for semantic segmentation of high resolution remote sensing images. arXiv 2018, arXiv:1805.02091. [Google Scholar]
- Find perimeter of objects in binary image, MATLAB bwperim, MathWorks China. Available online: http://in.mathworks.com/help/images/ref/bwperim.html (accessed on 13 July 2021).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Erosion (morphology) | Encyclopedia Article by TheFreeDictionary, China. Available online: https://encyclopedia.thefreedictionary.com/Erosion+(morphology) (accessed on 13 July 2021).
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, B.; Poullis, C. Semantic segmentation from remote sensor data and the exploitation of latent learning for classification of auxiliary tasks. arXiv 2019, arXiv:1912.09216. [Google Scholar]
- Chen, J.; Wang, C.; Zhang, H.; Wu, F.; Zhang, B.; Lei, W. Automatic detection of low-rise gable-roof building from single submeter SAR images based on local multilevel segmentation. Remote Sens. 2017, 9, 263. [Google Scholar] [CrossRef] [Green Version]
- Hong, Z.; Ming, D.; Zhou, K.; Guo, Y.; Lu, T. Road extraction from a high spatial resolution remote sensing image based on richer convolutional features. IEEE Access 2018, 6, 46988–47000. [Google Scholar] [CrossRef]
- Ehrig, M.; Euzenat, J. Relaxed precision and recall for ontology matching. In Proceedings of the K-Cap 2005 Workshop on Integrating Ontology, Banff, AB, Canada, 2 October 2005; pp. 25–32. [Google Scholar]
- Saito, S.; Aoki, Y. Building and road detection from large aerial imagery. SPIE/IS&T Electron. Imaging. 2015, 9405, 3–14. [Google Scholar] [CrossRef]
- Saito, S.; Yamashita, T.; Aoki, Y. Multiple object extraction from aerial imagery with convolutional neural networks. Electron. Imaging 2016, 60, 1–9. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J.; Huang, K.; Liang, K.; Yu, Y. Fastfcn: Rethinking dilated convolution in the backbone for semantic segmentation. arXiv 2019, arXiv:1903.11816. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar] [CrossRef] [Green Version]












| Model | HED | RCF | BDCN | DRC | ME-Net |
|---|---|---|---|---|---|
| Learning rate | 1e-6 | 1e-6 | 1e-6 | 1e-3 | 1e-6 |
| Momentum | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| Weight decay | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Batch size | 10 | 10 | 1 | 1 | 1 |
| Epoch | 30, 30, 10, 10 | 30, 30, 10, 10 | 30, 30, 10, 10 | 8, 8, 4,8 | 30, 30, 10, - |
| Step size (proportion) | 1/3 | 1/3 | 1/4 | 1/4 | 1/4 |
| Parameter | 14,716,171 | 14,803,781 | 16,302,712 | 32,336,202 | 16,302,925 |
| Training Time (h) | 5.5, 7.5, 10.8, 9.8 | 39.0, 16.5, 28.3, 31.8 | 61.0, 29.6, 51.0, 57.0 | 26.6, 18.4, 63.7, 97.6 | 43.5, 31.1, 42.5, - |
| Model | Scheme | OA (%) | F1 (%) | Precision (%) | Recall (%) | Kappa (%) | IoU (%) | Ene (%) |
|---|---|---|---|---|---|---|---|---|
| HED | strict relaxed | 87.99, 90.28 | 17.08, 41.82 | 9.38, 26.78 | 95.31, 95.40 | 15.08, 38.63 | 9.34, 26.66 | 18.74 |
| DRC | strict relaxed | 91.56, 92.91 | 17.11, 36.90 | 9.80, 24.98 | 67.06, 70.54 | 15.18, 35.88 | 9.35, 23.84 | 10.80 |
| RCF | strict relaxed | 93.99, 96.25 | 29.07, 64.38 | 17.17, 48.71 | 94.84, 94.92 | 27.48, 63.36 | 17.01, 48.26 | 3.84 |
| BDCN | strict relaxed | 95.07, 97.20 | 33.42, 69.84 | 20.26, 55.11 | 95.21, 95.30 | 31.96, 69.25 | 20.06, 54.55 | 2.42 |
| ME-Net | strict relaxed | 97.34, 98.75 | 44.58, 76.89 | 30.54, 70.73 | 82.50, 84.21 | 43.51, 79.19 | 28.68, 66.43 | 1.98 |
| Model | Scheme | OA (%) | F1 (%) | Precision (%) | Recall (%) | Kappa (%) | IoU (%) | Ene (%) |
|---|---|---|---|---|---|---|---|---|
| HED | strict relaxed | 74.61, 82.24 | 19.31, 53.07 | 10.87, 38.17 | 86.19, 87.03 | 13.92, 45.95 | 10.69, 37.52 | 37.90 |
| DRC | strict relaxed | 74.18, 80.99 | 17.28, 47.78 | 9.74, 34.35 | 76.52, 78.45 | 11.76, 41.16 | 9.46, 33.35 | 24.56 |
| RCF | strict relaxed | 79.66, 87.39 | 23.48, 61.59 | 13.54, 47.05 | 88.54, 89.17 | 18.50, 56.68 | 13.30, 46.24 | 19.38 |
| BDCN | strict relaxed | 82.24, 89.72 | 25.82, 65.32 | 15.14, 51.77 | 87.69, 88.48 | 21.08, 61.82 | 14.83, 50.69 | 11.94 |
| ME-Net | strict relaxed | 90.99, 95.00 | 28.99, 62.69 | 20.07, 63.81 | 52.19, 61.61 | 25.18, 67.35 | 16.95, 53.91 | 5.78 |
| Model | Scheme | OA (%) | F1 (%) | Precision (%) | Recall (%) | Kappa (%) | IoU (%) | Ene (%) |
|---|---|---|---|---|---|---|---|---|
| HED | strict relaxed | 81.29, 82.64 | 5.63, 17.42 | 2.96, 10.15 | 57.05, 61.35 | 3.84, 14.52 | 2.89, 9.93 | 25.10 |
| DRC | strict relaxed | 89.86, 90.89 | 7.99, 22.77 | 4.38, 14.67 | 45.02, 50.84 | 6.32, 21.82 | 4.16, 13.92 | 19.24 |
| RCF | strict relaxed | 89.61, 91.57 | 13.34, 38.51 | 7.26, 25.10 | 81.81, 82.70 | 11.76, 36.67 | 7.15, 24.70 | 19.20 |
| BDCN | strict relaxed | 88.55, 90.61 | 12.84, 37.49 | 6.94, 23.91 | 86.25, 86.85 | 11.23, 35.09 | 6.86, 23.64 | 15.84 |
| ME-Net | strict relaxed | 94.00, 95.51 | 17.49, 45.52 | 10.11, 34.03 | 65.01, 68.75 | 16.07, 46.91 | 9.58, 32.27 | 3.32 |
| Model | ODS-F (Ours) | ODS-F (Report) | OIS-F (Ours) | OIS-F (Report) |
|---|---|---|---|---|
| HED | 0.787 | 0.790 | 0.804 | 0.808 |
| DRC | 0.789 | 0.802 | 0.806 | 0.818 |
| RCF | 0.792 | 0.806 | 0.807 | 0.823 |
| BDCN | 0.806 | 0.806 | 0.822 | 0.826 |
| Model | JointNet (%) | FastFCN (%) | DeepLabv3+ (%) | EU-Net (%) | Our ME-Net (%) |
|---|---|---|---|---|---|
| F1-score | 27.31 | 13.73 | 21.92 | 28.83 | 28.99 |
| IoU | 15.82 | 7.37 | 12.31 | 16.84 | 16.95 |
| Model | FastFCN (%) | DeepLabv3+ (%) | EU-Net (%) | Our ME-Net (%) |
|---|---|---|---|---|
| F1-score | 11.18 | 14.84 | 20.47 | 17.49 |
| IoU | 5.92 | 8.01 | 11.40 | 9.58 |
| Dataset | Model | OA (%) | F1-Score (%) | IoU (%) |
|---|---|---|---|---|
| Jiangbei New Area | ME-Net (remove EM and local loss) | 97.20 | 69.84 | 54.55 |
| ME-Net (remove EM) | 97.37 | 70.98 | 55.91 | |
| ME-Net | 98.75 | 76.89 | 66.43 | |
| Massachusetts | ME-Net (remove EM and local loss) | 89.72 | 65.32 | 50.69 |
| ME-Net (remove EM) | 89.87 | 65.63 | 51.05 | |
| ME-Net | 95.00 | 62.69 | 53.91 | |
| Inria | ME-Net (remove EM and local loss) | 90.61 | 37.49 | 23.64 |
| ME-Net (remove EM) | 91.14 | 38.64 | 24.59 | |
| ME-Net | 95.51 | 45.52 | 32.27 |
| Training Dataset | Testing Dataset | OA (%) | F1-score (%) | IoU (%) |
|---|---|---|---|---|
| Jiangbei New Area | Jiangbei New Area | 98.75 | 76.89 | 66.43 |
| Massachusetts | 95.53 | 20.16 | 17.87 | |
| Inria | 98.03 | 29.43 | 23.31 | |
| Massachusetts | Jiangbei New Area | 98.06 | 28.21 | 23.32 |
| Massachusetts | 95.00 | 62.69 | 53.91 | |
| Inria | 97.46 | 25.13 | 19.09 | |
| Inria | Jiangbei New Area | 95.95 | 43.20 | 31.29 |
| Massachusetts | 92.11 | 40.45 | 33.04 | |
| Inria | 95.51 | 45.52 | 32.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, X.; Li, X.; Zhang, C.; Han, W.; Li, E.; Liu, W.; Zhang, L. ME-Net: A Multi-Scale Erosion Network for Crisp Building Edge Detection from Very High Resolution Remote Sensing Imagery. Remote Sens. 2021, 13, 3826. https://doi.org/10.3390/rs13193826
Wen X, Li X, Zhang C, Han W, Li E, Liu W, Zhang L. ME-Net: A Multi-Scale Erosion Network for Crisp Building Edge Detection from Very High Resolution Remote Sensing Imagery. Remote Sensing. 2021; 13(19):3826. https://doi.org/10.3390/rs13193826
Chicago/Turabian StyleWen, Xiang, Xing Li, Ce Zhang, Wenquan Han, Erzhu Li, Wei Liu, and Lianpeng Zhang. 2021. "ME-Net: A Multi-Scale Erosion Network for Crisp Building Edge Detection from Very High Resolution Remote Sensing Imagery" Remote Sensing 13, no. 19: 3826. https://doi.org/10.3390/rs13193826
APA StyleWen, X., Li, X., Zhang, C., Han, W., Li, E., Liu, W., & Zhang, L. (2021). ME-Net: A Multi-Scale Erosion Network for Crisp Building Edge Detection from Very High Resolution Remote Sensing Imagery. Remote Sensing, 13(19), 3826. https://doi.org/10.3390/rs13193826