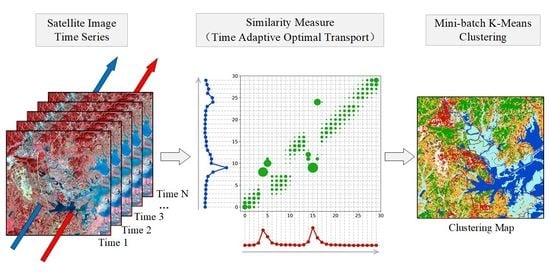
Satellite Image Time Series Clustering via Time Adaptive Optimal Transport
Abstract
:1. Introduction
- All images contained in a SITS have to be considered simultaneously and a comprehensive judgement depending heavily on an expert’s knowledge has to be made.
- The land cover type of a SITS may change, especially when the time series is long and, thus, the class label itself is hard to decide in some cases.
- SITS data now have a higher temporal resolution so that labeled training samples can merely keep pace with the high data acquisition frequency.
- Pathological alignment: A rational alignment between time series should be feature-to-feature and uniformly balanced, but DTW sometimes can lead to pathological alignment as shown by Figure 1a, where one point in a time series is mapped to nearly all points in the other time series, and this type of extreme alignment always ends with undesirable results.
- Spike noise: DTW is sensitive to spike noise as shown by Figure 1b,c, where a spike noise point easily disarranges the original alignment. Unluckily for SITS, spike noises such as cloud or cloud shadow pixels are ubiquitous and we cannot assume cloud-contaminated pixels will always be detected and removed completely.
- Limited capacity: The search space of optimal alignment is limited by DTW due to its rules of continuity, monotonicity, and boundary conditions. In theory, a fully-connected alignment can have a larger capacity and a higher flexibility for a more precise similarity.
2. Materials and Methods
2.1. Alignment-Based Similarity Measures
2.2. Time Adaptive Optimal Transport
2.3. SITS Clustering with TAOT
3. Results
3.1. Performance Metrics
3.2. Reunion Island Dataset
3.3. Poyang Lake Dataset
3.4. Extraction of Parameters
4. Discussion
4.1. Alignments Generated by TAOT
4.2. Capacity of TAOT
4.3. Limitations of TAOT
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Petitjean, F.; Inglada, J.; Gançarski, P. Satellite image time series analysis under time warping. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3081–3095. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Shen, H.; Li, H.; Xia, G.; Gamba, P.; Zhang, L. Multi-feature combined cloud and cloud shadow detection in GaoFen-1 wide field of view imagery. Remote Sens. Environ. 2017, 191, 342–358. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Zhang, G.; Zhu, X.; Pan, H.; Jiang, Y.; Zhou, P.; Wang, X. Triple linear-array image geometry model of ZiYuan-3 surveying satellite and its validation. Int. J. Image Data Fusion 2013, 4, 33–51. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Justice, C.; Townshend, J.; Vermote, E.; Masuoka, E.; Wolfe, R.; Saleous, N.; Roy, D.; Morisette, J. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Williams, D.L.; Goward, S.; Arvidson, T. Landsat. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Dedieu, G. Assessing the robustness of Random Forests to map land cover with high resolution satellite image time series over large areas. Remote Sens. Environ. 2016, 187, 156–168. [Google Scholar] [CrossRef]
- Inglada, J.; Vincent, A.; Arias, M.; Tardy, B.; Morin, D.; Rodes, I. Operational High Resolution Land Cover Map Production at the Country Scale Using Satellite Image Time Series. Remote Sens. 2017, 9, 95. [Google Scholar] [CrossRef] [Green Version]
- Khiali, L.; Ndiath, M.; Alleaume, S.; Ienco, D.; Ose, K.; Teisseire, M. Detection of spatio-temporal evolutions on multi-annual satellite image time series: A clustering based approach. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 103–119. [Google Scholar] [CrossRef]
- Gonçalves, H.; Gonçalves, J.A.; Corte-Real, L. Measures for an objective evaluation of the geometric correction process quality. IEEE Geosci. Remote Sens. Lett. 2009, 6, 292–296. [Google Scholar] [CrossRef]
- Habib, A.; Han, Y.; Xiong, W.; He, F.; Zhang, Z.; Crawford, M. Automated ortho-rectification of UAV-based hyperspectral data over an agricultural field using frame RGB imagery. Remote Sens. 2016, 8, 796. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.H.; Tsai, P.H.; Lai, K.H.; Chen, J.Y. Cloud removal from multitemporal satellite images using information cloning. IEEE Trans. Geosci. Remote Sens. 2012, 51, 232–241. [Google Scholar] [CrossRef]
- Hu, C.; Huo, L.Z.; Zhang, Z.; Tang, P. Multi-temporal landsat data automatic cloud removal using poisson blending. IEEE Access 2020, 8, 46151–46161. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Marais Sicre, C.; Dedieu, G. Effect of training class label noise on classification performances for land cover mapping with satellite image time series. Remote Sens. 2017, 9, 173. [Google Scholar] [CrossRef] [Green Version]
- Csillik, O.; Belgiu, M.; Asner, G.P.; Kelly, M. Object-based time-constrained dynamic time warping classification of crops using Sentinel-2. Remote Sens. 2019, 11, 1257. [Google Scholar] [CrossRef] [Green Version]
- Lampert, T.; Lafabregue, B.; Gançarski, P. Constrained distance based k-means clustering for satellite image time-series. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2419–2422. [Google Scholar]
- Santos, L.A.; Ferreira, K.R.; Camara, G.; Picoli, M.C.; Simoes, R.E. Quality control and class noise reduction of satellite image time series. ISPRS J. Photogramm. Remote Sens. 2021, 177, 75–88. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Kong, Y.L.; Huang, Q.; Wang, C.; Chen, J.; Chen, J.; He, D. Long short-term memory neural networks for online disturbance detection in satellite image time series. Remote Sens. 2018, 10, 452. [Google Scholar] [CrossRef] [Green Version]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Gonçalves, R.; Zullo, J.; Amaral, B.F.D.; Coltri, P.P.; Sousa, E.P.M.D.; Romani, L.A.S. Land use temporal analysis through clustering techniques on satellite image time series. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2173–2176. [Google Scholar]
- Zhang, Y.; Zhao, H. Land–use and land-cover change detection using dynamic time warping–based time series clustering method. Can. J. Remote Sens. 2020, 46, 67–83. [Google Scholar] [CrossRef]
- Fu, T.c. A review on time series data mining. Eng. Appl. Artif. Intell. 2011, 24, 164–181. [Google Scholar] [CrossRef]
- Mori, U.; Mendiburu, A.; Lozano, J.A. Similarity measure selection for clustering time series databases. IEEE Trans. Knowl. Data Eng. 2015, 28, 181–195. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Müller, M. Dynamic time warping. In Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; pp. 69–84. [Google Scholar]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Weber, J.; Petitjean, F.; Gançarski, P. Towards efficient satellite image time series analysis: Combination of dynamic time warping and quasi-flat zones. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4387–4390. [Google Scholar]
- Mondal, S.; Jeganathan, C. Mountain agriculture extraction from time-series MODIS NDVI using dynamic time warping technique. Int. J. Remote Sens. 2018, 39, 3679–3704. [Google Scholar] [CrossRef]
- Li, M.; Bijker, W. Vegetable classification in Indonesia using Dynamic Time Warping of Sentinel-1A dual polarization SAR time series. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 268–280. [Google Scholar] [CrossRef]
- Moola, W.S.; Bijker, W.; Belgiu, M.; Li, M. Vegetable mapping using fuzzy classification of Dynamic Time Warping distances from time series of Sentinel-1A images. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102405. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, M.; Liu, K.; Xie, J.; Xu, H. Using NDVI time series to diagnose vegetation recovery after major earthquake based on dynamic time warping and lower bound distance. Ecol. Indic. 2018, 94, 52–61. [Google Scholar] [CrossRef]
- Maus, V.; Câmara, G.; Cartaxo, R.; Sanchez, A.; Ramos, F.M.; De Queiroz, G.R. A time-weighted dynamic time warping method for land-use and land-cover mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3729–3739. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, J. Forest-Type Classification Using Time-Weighted Dynamic Time Warping Analysis in Mountain Areas: A Case Study in Southern China. Forests 2019, 10, 1040. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Lin, L.; Lu, W.; Meng, Y. Landsat time series clustering under modified Dynamic Time Warping. In Proceedings of the 2016 4th International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Guangzhou, China, 4–6 July 2016; pp. 62–66. [Google Scholar]
- Belgiu, M.; Zhou, Y.; Marshall, M.; Stein, A. Dynamic time warping for crops mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 947–951. [Google Scholar] [CrossRef]
- Dong, Q.; Chen, X.; Chen, J.; Zhang, C.; Liu, L.; Cao, X.; Zang, Y.; Zhu, X.; Cui, X. Mapping winter wheat in North China using Sentinel 2A/B data: A method based on phenology-time weighted dynamic time warping. Remote Sens. 2020, 12, 1274. [Google Scholar] [CrossRef] [Green Version]
- Keogh, E.J.; Pazzani, M.J. Derivative dynamic time warping. In Proceedings of the 2001 SIAM International Conference on Data Mining, Chicago, IL, USA, 5 April 2021; SIAM: Philadelphia, PA, USA, 2001; pp. 1–11. [Google Scholar]
- Zhang, Z.; Tang, P.; Duan, R. Dynamic time warping under pointwise shape context. Inf. Sci. 2015, 315, 88–101. [Google Scholar] [CrossRef]
- Zhang, Z.; Tavenard, R.; Bailly, A.; Tang, X.; Tang, P.; Corpetti, T. Dynamic Time Warping under limited warping path length. Inf. Sci. 2017, 393, 91–107. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Tang, P.; Corpetti, T. Time Adaptive Optimal Transport: A Framework of Time Series Similarity Measure. IEEE Access 2020, 8, 149764–149774. [Google Scholar] [CrossRef]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin, Germany, 2008; Volume 338. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational optimal transport: With applications to data science. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Santambrogio, F. Optimal transport for applied mathematicians. Birkäuser N. Y. 2015, 55, 94. [Google Scholar]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vis. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Ling, H.; Okada, K. An efficient earth mover’s distance algorithm for robust histogram comparison. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 840–853. [Google Scholar] [CrossRef] [PubMed]
- Courty, N.; Flamary, R.; Tuia, D.; Rakotomamonjy, A. Optimal transport for domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1853–1865. [Google Scholar] [CrossRef]
- Pele, O.; Werman, M. Fast and robust earth mover’s distances. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 460–467. [Google Scholar]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. Adv. Neural Inf. Process. Syst. 2013, 26, 2292–2300. [Google Scholar]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the KDD Workshop, Seattle, WA, USA, 31 July 1994; pp. 359–370. [Google Scholar]
- Ratanamahatana, C.A.; Keogh, E. Making time-series classification more accurate using learned constraints. In Proceedings of the 2004 SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 22 April 2014; SIAM: Philadelphia, PA, USA, 2004; pp. 11–22. [Google Scholar]
- Jeong, Y.S.; Jeong, M.K.; Omitaomu, O.A. Weighted dynamic time warping for time series classification. Pattern Recognit. 2011, 44, 2231–2240. [Google Scholar] [CrossRef]
- Myers, C.; Rabiner, L.; Rosenberg, A. Performance tradeoffs in dynamic time warping algorithms for isolated word recognition. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 623–635. [Google Scholar] [CrossRef]
- Keogh, E.J.; Pazzani, M.J. Scaling up dynamic time warping for datamining applications. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 285–289. [Google Scholar]
- Cai, Q.; Chen, L.; Sun, J. Piecewise statistic approximation based similarity measure for time series. Knowl.-Based Syst. 2015, 85, 181–195. [Google Scholar] [CrossRef]
- Geler, Z.; Kurbalija, V.; Radovanović, M.; Ivanović, M. Impact of the Sakoe-Chiba band on the DTW time series distance measure for kNN classification. In International Conference on Knowledge Science, Engineering and Management; Springer: Cham, Switzerland, 2014; pp. 105–114. [Google Scholar]
- Górecki, T.; Łuczak, M. The influence of the Sakoe–Chiba band size on time series classification. J. Intell. Fuzzy Syst. 2019, 36, 527–539. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. A metric for distributions with applications to image databases. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 7 January 1998; pp. 59–66. [Google Scholar]
- Piccoli, B.; Rossi, F. Generalized Wasserstein distance and its application to transport equations with source. Arch. Ration. Mech. Anal. 2014, 211, 335–358. [Google Scholar] [CrossRef] [Green Version]
- Robin, Y.; Yiou, P.; Naveau, P. Detecting changes in forced climate attractors with Wasserstein distance. Nonlinear Process. Geophys. 2017, 24, 393. [Google Scholar] [CrossRef] [Green Version]
- Kolouri, S.; Park, S.R.; Thorpe, M.; Slepcev, D.; Rohde, G.K. Optimal Mass Transport: Signal processing and machine-learning applications. IEEE Signal Process. Mag. 2017, 34, 43–59. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, Oakland, CA, USA, 21 June 1967; Volume 1, pp. 281–297. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Chavan, M.; Patil, A.; Dalvi, L.; Patil, A. Mini Batch K-Means Clustering on Large Dataset. Int. J. Sci. Eng. Technol. Res. 2015, 4, 1356–1358. [Google Scholar]
- Rand, W.M. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Liu, H.; Gong, P.; Wang, J.; Clinton, N.; Bai, Y.; Liang, S. Annual dynamics of global land cover and its long-term changes from 1982 to 2015. Earth Syst. Sci. Data 2020, 12, 1217–1243. [Google Scholar] [CrossRef]
- Lin, T.; Ho, N.; Cuturi, M.; Jordan, M.I. On the complexity of approximating multimarginal optimal transport. arXiv 2019, arXiv:1910.00152. [Google Scholar]
- Carriere, M.; Cuturi, M.; Oudot, S. Sliced Wasserstein kernel for persistence diagrams. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 664–673. [Google Scholar]















| Class ID | Class Name | Number of Samples | Percentage |
|---|---|---|---|
| 1 | Urban and built-up | 4647 | 25.86% |
| 2 | Forests | 4000 | 22.26% |
| 3 | Sparse vegetation | 3398 | 18.91% |
| 4 | Rocks and bare soil | 2588 | 14.40% |
| 5 | Grassland | 1290 | 7.18% |
| 6 | Sugarcane crops | 1531 | 8.52% |
| 7 | Water | 519 | 2.89% |
| Total | 17,973 | 100.00% |
| Similarity Measure | ED | DTW | SC-DTW | PDTW | TWDTW | TAOT |
|---|---|---|---|---|---|---|
| Adjusted Rand Score | 0.339 | 0.340 | 0.382 | 0.363 | 0.385 | 0.422 |
| Cohen Kappa Score | 0.433 | 0.409 | 0.458 | 0.458 | 0.453 | 0.554 |
| Overall Accuracy | 0.520 | 0.494 | 0.540 | 0.537 | 0.535 | 0.627 |
| Weighted F1 Score | 0.544 | 0.512 | 0.555 | 0.562 | 0.551 | 0.652 |
| Similarity Measure | ED | DTW | SC-DTW | PDTW | TWDTW | TAOT |
|---|---|---|---|---|---|---|
| Adjusted Rand Score | 0.337 ± 0.043 | 0.335 ± 0.043 | 0.339 ± 0.043 | 0.332 ± 0.042 | 0.339 ± 0.042 | 0.352 ± 0.043 |
| Cohen Kappa Score | 0.306 ± 0.113 | 0.312 ± 0.118 | 0.311 ± 0.118 | 0.312 ± 0.113 | 0.309 ± 0.116 | 0.326 ± 0.117 |
| Overall Accuracy | 0.406 ± 0.101 | 0.410 ± 0.106 | 0.409 ± 0.106 | 0.411 ± 0.102 | 0.408 ± 0.105 | 0.424 ± 0.104 |
| Weighted F1 Score | 0.421 ± 0.108 | 0.428 ± 0.114 | 0.427 ± 0.114 | 0.428 ± 0.109 | 0.425 ± 0.112 | 0.446 ± 0.111 |
| Class ID | Class Name | Number of Samples | Percentage |
|---|---|---|---|
| 1 | Cropland | 47,181 | 27.68% |
| 2 | Forest | 56,115 | 32.92% |
| 3 | Grassland | 2937 | 1.72% |
| 4 | Water | 54,262 | 31.83% |
| 5 | Impervious surface | 9192 | 5.39% |
| 6 | Bareland | 766 | 0.45% |
| Total | 170,453 | 100.00% |
| Similarity Measure | ED | DTW | SC-DTW | PDTW | TWDTW | TAOT |
|---|---|---|---|---|---|---|
| Adjusted Rand Score | 0.725 | 0.723 | 0.724 | 0.711 | 0.732 | 0.750 |
| Cohen Kappa Score | 0.714 | 0.723 | 0.728 | 0.716 | 0.731 | 0.749 |
| Overall Accuracy | 0.785 | 0.792 | 0.796 | 0.786 | 0.798 | 0.813 |
| Weighted F1 Score | 0.831 | 0.839 | 0.842 | 0.833 | 0.844 | 0.857 |
| Similarity Measure | ED | DTW | SC-DTW | PDTW | TWDTW | TAOT |
|---|---|---|---|---|---|---|
| Adjusted Rand Score | 0.737 ± 0.046 | 0.728 ± 0.032 | 0.730 ± 0.035 | 0.713 ± 0.039 | 0.737 ± 0.031 | 0.757 ± 0.030 |
| Cohen Kappa Score | 0.627 ± 0.124 | 0.610 ± 0.161 | 0.627 ± 0.138 | 0.599 ± 0.159 | 0.628 ± 0.154 | 0.637 ± 0.150 |
| Overall Accuracy | 0.715 ± 0.105 | 0.703 ± 0.129 | 0.716 ± 0.114 | 0.695 ± 0.127 | 0.716 ± 0.126 | 0.723 ± 0.123 |
| Weighted F1 Score | 0.746 ± 0.111 | 0.736 ± 0.138 | 0.747 ± 0.120 | 0.726 ± 0.133 | 0.748 ± 0.131 | 0.754 ± 0.128 |
| Similarity Measure | ED | DTW | SC-DTW | PDTW | TWDTW | TAOT |
|---|---|---|---|---|---|---|
| Reunion Island Dataset | n/a | n/a | r = 3 | n = 5 | = 800,000, = 0.1, = 100 | = 15, w = 400,000 |
| Poyang Lake Dataset | n/a | n/a | r = 3 | n = 21 | = 600,000, = 0.2, = 100 | = 12.5, w = 3,500,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Tang, P.; Zhang, W.; Tang, L. Satellite Image Time Series Clustering via Time Adaptive Optimal Transport. Remote Sens. 2021, 13, 3993. https://doi.org/10.3390/rs13193993
Zhang Z, Tang P, Zhang W, Tang L. Satellite Image Time Series Clustering via Time Adaptive Optimal Transport. Remote Sensing. 2021; 13(19):3993. https://doi.org/10.3390/rs13193993
Chicago/Turabian StyleZhang, Zheng, Ping Tang, Weixiong Zhang, and Liang Tang. 2021. "Satellite Image Time Series Clustering via Time Adaptive Optimal Transport" Remote Sensing 13, no. 19: 3993. https://doi.org/10.3390/rs13193993
APA StyleZhang, Z., Tang, P., Zhang, W., & Tang, L. (2021). Satellite Image Time Series Clustering via Time Adaptive Optimal Transport. Remote Sensing, 13(19), 3993. https://doi.org/10.3390/rs13193993