Analyzing Changes in Frozen Soil in the Source Region of the Yellow River Using the MODIS Land Surface Temperature Products
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methodology
3.1. Estimating the Mean Daily LST Using MODIS Data
3.2. Estimating the Distribution of Permafrost
3.3. Estimating the Maximum Thickness of the Seasonally-Frozen Ground and the Active Layer Thickness of the Permafrost
4. Results
4.1. Validation of the Mean Daily LST Estimated by Remote Sensing
4.2. Validation of the Simulated Distribution of the Permafrost by Remote Sensing
4.3. Validation of the MTSFG Estimated by Remote Sensing
4.4. Historical Change in the Frozen Soil
4.5. Sensitivity Analysis of the Different Parameterizations for the Mapping of the Frozen Soil
5. Discussion
5.1. Comparison with Previous Similar Studies
5.2. Uncertainties and Limitations of this Study
6. Conclusions
- (1)
- A multiple linear regression model with different coefficients in the cold season and warm season was developed, and it showed excellent aptitude for the estimation of the mean daily LST. Comparisons with the in-situ observations indicate that the method proposed in this study can accurately estimate the spatial distribution of permafrost and the changes in the MTSFG using the remote sensing LST data.
- (2)
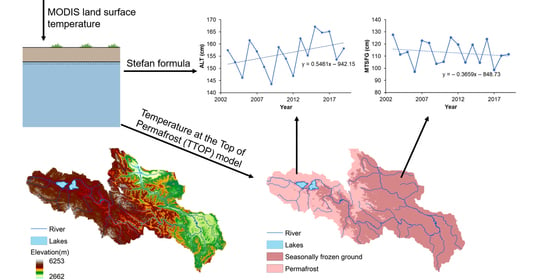
- The results of the TTOP model suggest that about 4.82% of the permafrost degraded to seasonally-frozen ground in the period from 2003 to 2019 in the SRYEARS. As estimated by the Stefan formula, the basin-averaged MTSFG decreased at a rate of 3.66 cm/10 years in the period from 2003 to 2019, and the basin-averaged ALT of permafrost increased at a rate of 5.46 cm/10 years.
- (3)
- The uncertainties in the estimation of the mean daily LST and the soil’s thermal conductivity are likely to have significant effects on the accuracy of the estimation of the spatial distribution of the permafrost and the MTSFG. The integration of more in-situ measurements, multi-source remote sensing data and models are required in future studies in order to improve the understanding of the frozen soil changes at the catchment scale.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LST | land surface temperature |
| GST | Ground surface temperature |
| MODIS | moderate-resolution imaging spectroradiometer |
| MTSFG | maximum thickness of seasonally-frozen ground(cm) |
| ALT | active layer thickness(cm) |
| SRYEARS | source region of the Yellow River |
| QTP | Qinghai–Tibetan Plateau |
| TTOP | Temperature at the Top of Permafrost |
References
- Woo, M.K. Permafrost Hydrology; Springer: Berlin/Heidelberg, Germany, 2012; pp. 5–6. [Google Scholar]
- Lawrence, D.M.; Koven, C.D.; Swenson, S.C.; Riley, W.J.; Slater, A.G. Permafrost thaw and resulting soil moisture changes regulate projected high-latitude CO2 and CH4 emissions. Environ. Res. Lett. 2015, 10, 9. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, M. The cold vadose zone: Hydrological and ecological significance of frozen-soil processes. Vadose Zone J. 2014, 13, 1. [Google Scholar] [CrossRef]
- Jin, X.Y.; Jin, H.J.; Iwahana, G.; Marchenko, S.S.; Liang, S.H. Impacts of climate-induced permafrost degradation on vegetation: A review. Adv. Clim. Chang. Res. 2020. [Google Scholar] [CrossRef]
- Walter, W.; Van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.; Bohn, T.J.; Zhao, L.; Li, J.; Liu, Q.; Zhou, B. Frozen soil degradation and its effects on surface hydrology in the northern Tibetan Plateau. J. Geophys. Res. Atmos. 2015, 120, 8276–8298. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Lei, H.; Yang, D.W.; Gao, B.; Wang, Y.H.; Cong, Z.T.; Fan, W.J. Long-term change in the depth of seasonally frozen ground and its ecohydrological impacts in the Qilian Mountains, northeastern Tibetan Plateau. J. Hydrol. 2016, 542, 204–221. [Google Scholar] [CrossRef]
- Gao, B.; Yang, D.W.; Qin, Y.; Wang, Y.H.; Li, H.Y.; Zhang, Y.L.; Zhang, T.J. Change in frozen soils and its effect on regional hydrology, upper Heihe Basin, northeastern Qinghai-Tibetan Plateau. Cryosphere 2018, 12, 657–673. [Google Scholar] [CrossRef] [Green Version]
- Niu, L.; Ye, B.S.; Li, J.; Sheng, Y. Effect of permafrost degradation on hydrological processes in typical basins with various permafrost coverage in Western China. Sci. China Earth Sci. 2011, 54, 615–624. [Google Scholar] [CrossRef]
- Zhang, W.J.; Yi, Y.H.; Kimball, J.S.; Kim, Y.; Song, K.C. Climatic controls on spring onset of the Tibetan Plateau Grasslands from 1982 to 2008. Remote Sens. 2015, 7, 16607–16622. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.; Li, J.; Wang, X.S. Impact of frozen soil changes on vegetation phenology in the source region of the Yellow River from 2003 to 2015. Theor. Appl. Climatol. 2020, 141, 1219–1234. [Google Scholar] [CrossRef]
- Chen, S.Y.; Liu, W.J.; Qin, X.; Liu, Y.S.; Zhang, T.Z.; Chen, K.L.; Hu, F.Z.; Ren, J.W.; Qin, D.H. Response characteristics of vegetation and soil environment to permafrost degradation in the upstream regions of the Shule River Basin. Environ. Res. Lett. 2012, 7, 189–190. [Google Scholar] [CrossRef] [Green Version]
- Wania, R. Integrating peatlands and permafrost into a dynamic global vegetation model: 1. Evaluation and sensitivity of physical land surface processes. Glob. Biogeochem. Cycle 2009, 23, 3. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.L.; Wang, H. Simulation of permafrost and seasonally frozen ground conditions on the Tibetan Plateau, 1981–2010. J. Geophys. Res. Atmos. 2013, 118, 5216–5230. [Google Scholar] [CrossRef]
- Wang, T.H.; Yang, D.W.; Fang, B.J.; Yang, W.C.; Qin, Y.; Wang, Y.H. Data-driven mapping of the spatial distribution and potential changes of frozen ground over the Tibetan Plateau. Sci. Total Environ. 2018, 649, 515–525. [Google Scholar] [CrossRef] [PubMed]
- Ran, Y.H.; Li, X.; Cheng, G.D.; Nan, Z.T.; Che, J.X.; Sheng, Y.; Wu, Q.B.; Jin, H.J.; Luo, D.L.; Tang, Z.G.; et al. Mapping the permafrost stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2020, 63, 1–18. [Google Scholar] [CrossRef]
- Smith, M.W.; Riseborough, D.W. Permafrost monitoring and detection of climate change. Permafr. Periglac. Process. 1996, 7, 301–309. [Google Scholar] [CrossRef]
- Stefan, J. Ueber die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. Berlin. 1891, 278, 269–286. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.Q.; Frauenfeld, O.; Zhang, T.J.; Wang, K.; Cao, B.; Zhong, X.Y.; Hang, S.; Mu, C.C. Response of seasonal soil freeze depth to climate change across China. Cryosphere 2017, 11, 1059–1073. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.H.; Yang, D.W.; Qin, Y.; Wang, Y.H.; Chen, Y.; Gao, B.; Yang, H.B. Historical and future changes of frozen ground in the upper Yellow River Basin. Glob. Planet. Chang. 2018, 162, 199–211. [Google Scholar] [CrossRef]
- Riseborough, D.; Shiklomanov, N.; Etzelmüller, B.; Gruber, S.; Marchenko, S. Recent advances in permafrost modelling. Permafr. Periglac. Process. 2008, 19, 137–156. [Google Scholar] [CrossRef]
- Wang, C.H.; Jin, S.L.; Wu, Z.Y.; Cui, Y. Evaluation and Application of the Estimation Methods of Frozen (Thawing) Depth over China. Adv. Earth Sci. 2009, 24, 132–141. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, G.H.; Yang, Y.T.; Yang, D.W.; Dafflon, B.; Lei, H.M.; Yang, H.B. Satellite-based simulation of soil freezing/thawing processes in the northeast Tibetan Plateau. Remote Sens. Environ. 2019, 231, 111269. [Google Scholar] [CrossRef]
- Langer, M.; Westermann, S.; Boike, J. Spatial and temporal variations of summer surface temperatures of wet polygonal tundra in Siberia-implications for MODIS LST based permafrost monitoring. Remote Sens. Environ. 2010, 114, 2059–2069. [Google Scholar] [CrossRef]
- Yang, Y.K.; Li, H.; Sun, L.; Du, Y.M.; Cao, B.; Liu, Q.H.; Zhu, J.S. Land surface temperature and emissivity separation from Gaofen-5 multispectral imager data. J. Remote Sens. 2019, 23, 1090–1104. (In Chinese) [Google Scholar] [CrossRef]
- Zou, D.F.; Zhao, L.; Wu, T.H.; Wu, X.D.; Pang, Q.Q.; Qiao, Y.P.; Wang, Z.W. Assessing the applicability of MODIS land surface temperature products in continuous permafrost regions in the central Tibetan Plateau. Glacier Permafrost. 2015, 37, 308–317. (In Chinese) [Google Scholar] [CrossRef]
- Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.; Avirmed, D.; Delaloye, R.; Elberling, B.; Etzelmüller, B.; Kholodov, A.; et al. Northern Hemisphere permafrost map based on TTOP modelling for 2000–2016 at 1 km2 scale. Earth Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
- Wang, R.; Dong, Z.B.; Zhou, Z.C. Effect of decreasing soil frozen depth on vegetation growth in the source region of the Yellow River for 1982–2015. Theor. Appl. Climatol. 2020, 140, 3–4. [Google Scholar] [CrossRef]
- Hu, Y.R.; Maskey, S.; Zhao, U.L. Streamflow trends and climate linkages in the source region of the Yellow River, China. Hydrol. Process. 2011, 25, 3399–3411. [Google Scholar] [CrossRef]
- Qin, Y.; Yang, D.W.; Gao, B.; Wang, T.H.; Chen, J.; Chen, Y.; Wang, Y.; Zheng, G. Impacts of climate warming on the frozen ground and eco-hydrology in the Yellow River source region, China. Sci. Total Environ 2017, 605–606, 830–841. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Xiong, A.Y. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Luo, D.L.; Jin, H.J.; Lin, L.; He, R.X.; Yang, S.Z.; Chang, X.L. New Progress on Permafrost Temperature and Thickness in the Source Area of the Huanghe River. Sci. Geogr. Sin. 2012, 32, 898–904. (In Chinese) [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations(FAO); International Institute for Applied Systems Analysis. China Soil Map Based Harmonized World Soil Database (HWSD) (v1.1) (2009); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Dai, Y.J.; Shang, G.W.; Duan, Q.Y.; Liu, B.Y.; Fu, S.H.; Niu, G.Y. Development of a China Dataset of Soil Hydraulic Parameters Using Pedotransfer Functions for Land Surface Modeling. J. Hydrometeorol. 2013, 14, 869–887. [Google Scholar] [CrossRef] [Green Version]
- Ran, Y.; Li, X. Progress, challenges and opportunities of permafrost mapping in China. Adv. Earth Sci. 2019, 34, 1015–1027. (In Chinese) [Google Scholar]
- Farouki, O.T. The thermal properties of soils in cold regions. Cold Reg. Sci. Technol. 1981, 5, 67–75. [Google Scholar] [CrossRef]
- Kersten, M.S. Laboratory research for the determination of the thermal properties of soils. J. Neurophysiol. 1948, 45, 667–697. [Google Scholar] [CrossRef]
- Li, W.P.; Zhao, L.; Wu, X.D.; Zhao, Y.H.; Fang, H.B.; Shi, W. Distribution of soils and landform relationships in the permafrost regions of Qinghai-Xizang (Tibetan) Plateau. Chin. Sci. Bull. 2015, 60, 2216–2226. (In Chinese) [Google Scholar] [CrossRef]
- Zou, D.F.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.J.; Wu, T.H.; Pang, Q.; Wang, W. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Ran, Y.H.; Li, X.; Jin, R.; Guo, J.W. Remote sensing of the mean annual surface temperature and surface frost number for mapping permafrost in China. Arct. Antarct. Alp. Res. 2015, 47, 255–265. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, B.; Che, T.; Dai, L.Y.; Wang, Z.Y. Estimating Mean Daily Surface Temperature over the Tibetan Plateau Based on MODIS LST Products. J. Glaciol. Geocryol. 2012, 34, 296–303. (In Chinese) [Google Scholar]
- Hu, J.N.; Zhao, S.P.; Nan, Z.T.; Wu, X.B.; Sun, X.H.; Cheng, G.D. An effective approach for mapping permafrost in a large area using subregion maps and satellite data. Permafr. Periglac. Process. 2020, 31, 548–560. [Google Scholar] [CrossRef]










| Station Name | Elevation(m) | Latitude | Longitude | Landcover | Starting and Ending Years of Observation | ||
|---|---|---|---|---|---|---|---|
| MTSFG | LST | Air Temperature & Precipitation | |||||
| Xinghai | 3323.2 | 35°35′ | 99°59′ | Steppe | 2003–2015 | 2003–2015 | 2003–2019 |
| Maduo | 4272.3 | 34°55′ | 98°13′ | Steppe | 2003–2015 | 2003–2015 | 2003–2019 |
| Maqin | 3719.0 | 34°29′ | 100°14′ | Meadow | 2003–2015 | 2003–2015 | 2003–2019 |
| Dari | 3967.5 | 33°45′ | 99°39′ | Meadow | 2003–2015 | 2003–2015 | 2003–2019 |
| Henan | 3500.0 | 34°44′ | 101°36′ | Meadow | 2003–2015 | 2003–2015 | 2003–2019 |
| Jiuzhi | 3628.5 | 33°26′ | 101°29′ | Meadow | 2003–2015 | 2003–2015 | 2003–2019 |
| Maqu | 3471.4 | 34°00′ | 102°05′ | Steppe | 2007–2015 | 2003–2015 | 2003–2019 |
| Zoige | 3441.4 | 33°35′ | 102°58′ | Meadow | 2003–2015 | 2003–2015 | 2003–2019 |
| Hong-yuan | 3491.6 | 32°48′ | 102°33′ | Meadow | 2003–2015 | 2003–2015 | 2003–2019 |
| Station Name | Latitude | Longitude | Elevation(m) | Drilling Time | Observed Type | Estimated Type in this Study | Estimated Type by Zou et al. [39] |
|---|---|---|---|---|---|---|---|
| CLP-1 | 34.25 | 97.85 | 4727 | 2010/8 | PF | PF | PF |
| CLP-2 | 34.25 | 97.85 | 4723 | 2010/8–9 | PF | PF | PF |
| CLP-3 | 34.27 | 97.87 | 4663 | 2010/8 | PF | PF | PF |
| CLP-4 | 34.32 | 97.9 | 4564 | 2010/8 | PF | PF | PF |
| YNG-1 | 34.4 | 97.95 | 4452 | 2010/8 | PF | PF | PF |
| YNG-2 | 34.43 | 97.93 | 4395 | 2010/8 | SFG | SFG | PF |
| YNG-3 | 34.5 | 97.97 | 4333 | 2010/8 | SFG | SFG | PF |
| XXH-1 | 34.65 | 98.43 | 4231 | 2010/8 | SFG | SFG | SFG |
| MDB | 34.85 | 98.55 | 4225 | 2010/9 | PF | PF | PF |
| K445 | 34.97 | 98.55 | 4288 | 2010/9 | PF | PF | PF |
| The Scheme For Thermal Conductivity Estimation | Regression Coefficients for the Estimation of the Mean Daily LST | ||||||
|---|---|---|---|---|---|---|---|
| a1 | a2 | a3 | a4 | b | |||
| Normal run | Johansen’s scheme | Warm season | 0.154 | 0.274 | 0.096 | 0.428 | 4.775 |
| Cold season | 0.109 | 0.229 | 0.104 | 0.341 | 7.802 | ||
| Exp1 | Kersten’s scheme | Warm season | 0.154 | 0.274 | 0.096 | 0.428 | 4.775 |
| Cold season | 0.109 | 0.229 | 0.104 | 0.341 | 7.802 | ||
| Exp2 | Johansen’s scheme | - | 0.170 | 0.307 | 0.111 | 0.442 | 5.564 |
| Exp3 | Johansen’s scheme | - | 0.25 | 0.25 | 0.25 | 0.25 | 0 |
| Station Name | Observed | Normal Run | Exp1 | Exp2 | Exp3 |
|---|---|---|---|---|---|
| CLP-1 | PF | PF | PF | PF | PF |
| CLP-2 | PF | PF | PF | PF | PF |
| CLP-3 | PF | PF | PF | PF | PF |
| CLP-4 | PF | PF | PF | PF | PF |
| YNG-1 | PF | PF | SFG | PF | PF |
| YNG-2 | SFG | SFG | SFG | PF | PF |
| YNG-3 | SFG | SFG | SFG | SFG | SFG |
| XXH-1 | SFG | SFG | SFG | SFG | SFG |
| MDB | PF | PF | PF | PF | PF |
| K445 | PF | PF | PF | PF | PF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Gao, B.; Gong, T.; Wang, B. Analyzing Changes in Frozen Soil in the Source Region of the Yellow River Using the MODIS Land Surface Temperature Products. Remote Sens. 2021, 13, 180. https://doi.org/10.3390/rs13020180
Cao H, Gao B, Gong T, Wang B. Analyzing Changes in Frozen Soil in the Source Region of the Yellow River Using the MODIS Land Surface Temperature Products. Remote Sensing. 2021; 13(2):180. https://doi.org/10.3390/rs13020180
Chicago/Turabian StyleCao, Huiyu, Bing Gao, Tingting Gong, and Bo Wang. 2021. "Analyzing Changes in Frozen Soil in the Source Region of the Yellow River Using the MODIS Land Surface Temperature Products" Remote Sensing 13, no. 2: 180. https://doi.org/10.3390/rs13020180
APA StyleCao, H., Gao, B., Gong, T., & Wang, B. (2021). Analyzing Changes in Frozen Soil in the Source Region of the Yellow River Using the MODIS Land Surface Temperature Products. Remote Sensing, 13(2), 180. https://doi.org/10.3390/rs13020180