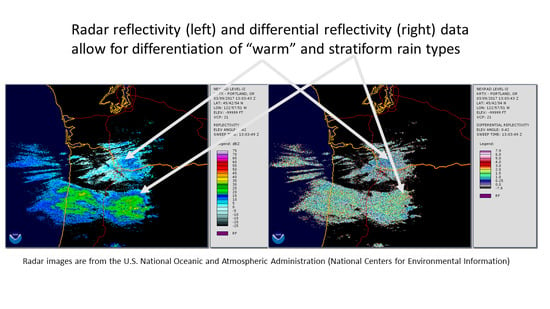
Distinguishing between Warm and Stratiform Rain Using Polarimetric Radar Measurements

Abstract

Modeled statistical differential reflectivity–reflectivity (i.e., Z_DR–Z_e) correspondences for no bright-band warm rain and stratiform bright-band rain are evaluated using measurements from an operational polarimetric weather radar and independent information about rain types from a vertically pointing profiler. It is shown that these relations generally fit observational data satisfactorily. Due to a relative abundance of smaller drops, Z_DR values for warm rain are, on average, smaller than those for stratiform rain of the same reflectivity by a factor of about two (in the logarithmic scale). A Z_DR–Z_e relation, representing a mean of such relations for warm and stratiform rains, can be utilized to distinguish between warm and stratiform rain types using polarimetric radar measurements. When a mean offset of observational Z_DR data is accounted for and reflectivities are greater than 16 dBZ, about 70% of stratiform rains and approximately similar amounts of warm rains are classified correctly using the mean Z_DR–Z_e relation when applied to averaged data. Since rain rate estimators for warm rain are quite different from other common rain types, identifying and treating warm rain as a separate precipitation category can lead to better quantitative precipitation estimations.

1. Introduction

Warm rain is formed mostly by the coalescence of cloud water droplets into rain drops taking place primarily in the atmosphere with temperatures above 0 °C (i.e., the freezing level temperature). Warm rain precipitation events have traditionally presented a challenge for weather radar-based quantitative precipitation estimation (QPE) [1]. Compared to stratiform rain drops, which typically originate from melting snowflakes that form and grow above the freezing level height, warm rain drops (for approximately the same rain rates) are, on average, (with some relatively rare exceptions [2]) much smaller and more numerous [3].

The atmospheric layer where snowflake melting takes place is usually manifested by the reflectivity enhancement, which is also known as the radar bright band, so stratiform rain is sometimes called bright-band (BB) rain, and warm rain is referred to as non-bright band (NBB) rain [3]. Reflectivity bright bands are usually accompanied by a drop in the correlation coefficient between horizontally and vertically polarized radar returns [4]. At higher radar frequencies, the attenuation of radar signals in liquid phase can enhance BB for nadir pointing measurements [5].

Due to differing drops size distribution (DSD) shapes, warm NBB and stratiform BB rains are characterized by distinctly different average relations between equivalent radar reflectivity factor (hereafter just reflectivity, Z_e) and rain rate, R (i.e., Z_e = aR^b relations) [3,6]. Such relations are often utilized for operational radar-based QPE using the multi-radar multi sensor (MRMS) approach [7]. The coefficients a in the warm NBB rain Z_e=aR^b relations are typically a factor of about 3 (on average) smaller than those for stratiform rain, while the exponents b could be close. This can lead to about 40% total rain accumulation underestimation when default stratiform BB rain or convective rain Z_e–R relations are applied to warm NBB rain [6].

While rain rate estimators that use polarimetric radar variables (e.g., specific differential phase, K_DP) can potentially provide more accurate QPE retrievals [8,9], applying these estimators for warm NBB rain is challenging, as smaller rain drops are more spherical than larger ones [10]; thus, dual-polarization signatures of such rain, especially at lower weather radar frequencies (e.g., at S-band) are often rather noisy [3]. As a result, reflectivity-based precipitation rate estimators are often used in practice. However, warm rain accumulations are climatologically important because the contributions of such rain to total annual liquid precipitation amounts are usually on the order of 20% on the US West coast [11]. Warm rain is more frequent over ocean [12,13].

For radar-based QPE improvements, it is important to differentiate between different rain types. Segregation procedures between stratiform and convective rain exist and are already incorporated in the MRMS approach [14]. Recently, mean statistical relations between differential reflectivity (i.e., Z_DR, which is defined as the logarithmic difference between horizontal and vertical polarization reflectivities) and reflectivity, Z_e, for warm NBB and stratiform BB rains were suggested [6]. These relations, which allow for statistical differentiation between these types of rain, were developed theoretically using observed DSDs. The objective of the current study was to evaluate the theoretically derived mean warm and stratiform rain Z_DR–Z_e theoretical relations with operational measurements from an S-band (wavelength ≈ 10 cm) Weather Surveillance Radar-1988 Doppler (WSR-88D) unit when the warm–stratiform rain segregation is independently known. Of particular interest was assessing the efficacy of differentiating between these rain types using observational data, which have measurement uncertainties and, possibly, biases.

2. Data and Methods

The mean statistical S-band Z_DR–Z_e relations for low radar beam tilt (≈0.5°) found in [6] through modeling using observed DSDs and independent identification of rain types are:

Z_DR = 6.8∙10⁻⁵Z_e^2.68 (for stratiform BB rain),

(1)

Z_DR = 3.2∙10⁻⁵Z_e^2.70 (for warm NBB rain),

(2)

where Z_DR is in decibels (dB) and Z_e is in decibels relative to 1 mm⁶m⁻³ (dBZ). These relations were derived using one-year long observations from the National Oceanic and Atmospheric Administration (NOAA) temporary observation sites near New Burn (EWN, 35.078°N, 77.046°W) and Old Fort (OFT, 35.643°N, 82.161°W), North Carolina.

Relations Equations (1) and (2) were developed in [6] using concurrent measurements from vertically pointing S-band profiler measurements, which were utilized to independently segregate warm NBB and stratiform BB rain profiles, and calculations of Z_e and Z_DR using DSDs measured by a quality-controlled Particle Size and Velocity (Parsivel) optical disdrometers [15], which were deployed next to the profilers. Reflectivity and differential reflectivity values (in linear units) were derived using formulas

Z_e = λ⁴π⁻⁵|K_w|⁻²<σ_h>,

(3)

Z_DR = (λ⁴π⁻⁵|K_w|⁻²<σ_h>)(λ⁴π⁻⁵|K_w|⁻²<σ_v>)⁻¹,

(4)

where λ is the radar wavelength, |K_w|² ≈ 0.93, σ_h and σ_v are backscatter cross-sections for horizontal and vertical polarizations, which are drop size and shape dependent, and the angle brackets denote the summation over DSD bin sizes in a unit volume and averaging over drop orientations. Drop shapes were approximated by oblate spheroids with aspect ratios dependent on drop size [10]. It was assumed that the distribution of zenith angles of drop symmetry axes was Gaussian with a 0° mean value and a 10° standard deviation. Size-dependent drop fall velocities, which are needed to calculate drop concentrations from disdrometer bin counts, were adopted from [16], and the backscatter cross-sections were calculated using the T-matrix method [17].

It can be seen from Equations (1) and (2) that for the same values of reflectivity, differential reflectivity values for warm NBB rain are, on average, about a factor of 2 (in the logarithmic scale) smaller than those for stratiform BB rain. It is because the former rain type contains larger relative amounts of smaller more spherical drops than the latter type. As shown in [6], the mean Z_DR–Z_e relations for these rain types have relatively little sensitivity to the choice of existing drop shape models, which relate an average rain drop oblateness to its size.

The operational weather radar data used in the current study came from the Portland, Oregon WSR-88D unit, which has a four-letter identifier KRTX. The KRTX radar is located at an altitude of about 0.5 km above mean sea level (MSL) at 45.715°N, 122.965°W. This radar is part of about 160 S-band polarimetric Doppler radars operated by the United States National Weather Service (NWS). These radars employ the simultaneous transmission and simultaneous reception of horizontally and vertically polarized waves. Level II WSR-88D reflectivity and differential reflectivity data, which are used in this study, are available from the Next-Generation radar (NEXRAD) archive at https://www.ncdc.noaa.gov/nexradinv/.

The NOAA Physical Sciences Laboratory (PSL) operated a temporary site at Troutdale (TDE), Oregon (45.5535°N, 122.3864°W, altitude 0.012 km MSL) as part of the Hydrometeorology Testbed (HMT) deployment to study atmosphere dynamics in the Columbia River gorge. Measurements from a NOAA PSL vertical pointing S-band profiler (S-Prof) [18] deployed at that site were used to independently differentiate between various types of rain, and the operational KRTX measurements above the TDE site were used to collect observational Z_DR–Z_e correspondence data.

The map locations of the KRTX and TDE sites are shown in Figure 1. The TDE site was located at a distance of about 48 km in the 111° azimuthal direction from the KRTX radar location. The data from the TDE observational site are available from the PSL HMT data archive at https://psl.noaa.gov/data/obs/datadisplay/archive/InactiveSites.html. A procedure to differentiate among different rain types using vertically pointing S-Prof data is based on analyzing the vertical profiles of radar moments and is described in [6]. Stratiform BB, warm NBB, and deep convective rain types are differentiated using this procedure. In general, rain type partitioning does not require absolute calibration of the vertically pointing radar.

In a precipitation measurement mode, WSR-88D units perform volume scans consisting of plan position indicator (PPI) measurements at different beam tilts, which generally range from 0.5° to 20° radar beam elevations. The WSR-88D beam width is about 1° (at a 3 dB level). Only the lowest beam tilt measurements from the KRTX radar were used in this study, because radar resolution volumes at higher beam tilts often were (at least partially) within regions of solid and/or melted precipitation. One volume scan takes about 6 min, which was a time interval between two consecutive lowest tilt KRTX measurements above the TDE site.

Identification of Different Rain Types

Figure 2 shows an example of a precipitation event observed at the TDE site by the vertically pointing S-Prof radar. In this example, the stratiform bright-band rain over the TDE site was observed during the time interval from about 13:00 UTC on 9 March 2016 to 10:00 UTC on 10 March 2016. The precipitating cloud system was very deep between these times with radar echo heights reaching 10 km MSL. The top of the radar bright-band is indicative of a freezing level height, which generally separates ice and melting hydrometeors. According to meteorological observations at the ground (not shown), the near-surface air temperatures throughout the event varied from about 7 to 14 °C with a warm front passage occurring approximately at 09:00 UTC on 10 March 2016. For this event, the KRTX polarimetric radar data were mostly collected from a layer of liquid precipitation below the layer of melting hydrometeors.

Warm NBB rain during the event shown in Figure 2 was observed during a time period between about 02:00 and 10:00 UTC on 9 March 2016. Although radar echoes for warm NBB rain could extend somewhat higher than the environmental freezing level due to atmospheric updrafts, the precipitation formation is still dominated by warm-rain processes.

Short periods of convective rain were also present during this rain event (mostly after 11:00 UTC on 10 March 2016) with a most significant one occurring at approximately 22:00 UTC on 10 March 2016. As warm rain, deep convective rain does not exhibit the bright-band, but its radar returns with high reflectivity cores reach much further above the environmental freezing level, and the ice phase plays an important role in the convective precipitation processes.

The KRTX measurements for the lowest radar beam measurements are sampled at a 0.25 km resolution. KRTX reflectivity and differential reflectivity values observed within a 1 km range from the TDE location and within 1° from the KRTX–TDE azimuthal direction were averaged in order to reduce measurement noise. To avoid ground clutter, the KRTX data were taken into consideration only when the copolar correlation coefficients between horizontally and vertically polarized radar echoes were greater than 0.9. The corresponding averages were used for further analysis. Estimates of the upper and lower KRTX radar beam edges are also shown in Figure 2. These estimates were calculated with accounting for mean atmospheric refraction and Earth’s sphericity [19]. To avoid contaminations of rain layer radar variables by the melting hydrometeors, the stratiform BB rain time periods were considered only when the upper KRTX beam edge estimates were lower than the bright band bottom by at least 0.2 km.

3. Results

3.1. Mean Z_DR–Z_e Correspondences for Different Rain Types

Precipitation events observed by the KRTX polarimetric operational radar over the TDE site during the January 2016–March 2017 period, when the independent information on rain-type partitioning from the S-Prof measurements was available, were further analyzed. To mitigate possible partial KRTX beam-filling effects, precipitation occurrences with a spatial coverage over 10 km and continuously lasting over 1 hour were considered. Figure 3 shows cumulative frequency scatter plots of observed KRTX differential reflectivity–reflectivity correspondences for stratiform BB and warm NBB rains. The best fit mean Z_DR–Z_e relations found previously in [6] for these two rain types through modeling are also shown.

It can be seen from Figure 3 that the reflectivities and differential reflectivities observed by the KRTX radar, on average, align well with the previously modeled mean theoretical Z_DR–Z_e correspondences for stratiform BB and warm NBB types of rain. This is an important result, especially given the fact that the theoretical relations were obtained using DSDs observed during the HMT Southeastern (HMT-SE) United States deployment, but the radar variables were observed by the radar near the U.S. West Coast. This fact indicates that a potential polarimetric radar-based differentiation between these rain types could have a rather general applicability.

According to the results of theoretical modeling in [6], a Z_DR–Z_e relation, which for the most part separates warm NBB from stratiform BB rain types, can be given as:

Z_DR = 4.8∙10⁻⁵Z_e^2.69,

(5)

which approximately corresponds to the mean of Equations (1) and (2). Most (≈80%) of stratiform rains exhibit theoretical differential reflectivities greater than those expressed by Equation (5), while most of the warm NBB rains are characterized by Z_DR values which are smaller than that. As modeled radar variables, observational data from the operational KRTX radar also show that on average, for a given reflectivity value, differential reflectivities of stratiform BB rains are greater by a factor of approximately 2 compared to warm NBB rains (when Z_DR is in the logarithmic scale).

However, radar measurement data are often quite noisy (especially differential reflectivity data at small Z_DR values). As can be seen from Figure 3, the observational data scatter of Z_DR–Z_e correspondences is rather substantial. This scatter is most significant for warm NBB rain at lower reflectivity values. On average, warm NBB rain reflectivities are smaller than those for stratiform BB rain. It is instructive to estimate the effectiveness of relation Equation (5) for differentiation between warm and stratiform rain using observational WSR-88D data. Differential reflectivity measurements can be especially noisy for small Z_DR values and subject to biases, as they are especially difficult to calibrate in the absolute sense for radars, which, as WSR-88D systems, do not have an option of pointing the radar beam vertically [20]. A general noisiness of differential reflectivity measurements is evident from Figure 3, since there are some negative values, whereas positive Z_DR values are expected in rain measurements.

To assess an average Z_DR bias in KRTX measurements, the mean differential reflectivity values for low radar reflectivities, which are typical for drizzle-like rain (i.e., 5 dBZ < Z_e < 10 dBZ) were calculated. Since drizzle drops are practically spherical, their Z_DR values are expected to be around 0 dB. Modeling results with observational DSDs and realistic rain drop shape models in [6] also indicate that mean Z_DR values are less than 0.1 dB when reflectivities are less than about 15 dBZ. However, for low reflectivity KRTX measurements, a mean differential reflectivity value was found to be approximately 0.3 dB. Then, this value was assumed to be a mean Z_DR offset (bias) for the KRTX radar dataset considered in this study. This is consistent with a few tenths of 1 dB Z_DR positive offset, which is also present between mean relations Equations (1) and (2) and the observational data in Figure 3.

With accounting for the mean 0.3 dB differential reflectivity offset found for low reflectivity drizzle-like rains, the mean residual biases of observational Z_DR values versus those predicted by modeling as given by Equations (1) and (2) are 0.05 dB and 0.12 dB, for BB and NBB warm rains, respectively. Corresponding standard deviations are 0.38 dB (for BB stratiform rains) and 0.4 dB (for NBB warm rains).

It is of particular interest to assess from WSR-88 observations (i.e., those shown as scatter plots in Figure 3) how well the relation Equation (5) can segregate BB stratiform and NBB warm rains. The analysis shows that Equation (5), where Z_e and Z_DR data are from the KRTX measurements, segregates the warm NBB and stratiform BB rain types (as independently inferred from the S-Prof measurements) with an overall effectiveness of about 65% when observed reflectivity values are greater than 16 dBZ. About 67% of observed stratiform BB rains exhibited Z_DR values that are greater than the one prescribed by Equation (5), while about 63% of detected warm NBB rain had differential reflectivities smaller than that. Without accounting for the differential reflectivity offset, the above percentages of the correct rain type differentiation using observed radar variables diminishes by approximately 5 percentage points.

A decrease in the overall effectiveness of segregating warm NBB and stratiform BB rain types using polarimetric radar observations compared to the results of theoretical modeling (i.e., 65% vs. 80%) can be attributed, in part, to uncertainties and noisiness of radar measurements. One way to increase the effectiveness of rain type identifications is to perform some additional averaging of reflectivity and differential reflectivity measurements. Applying the suggested here segregation approach to additionally averaged data shows that averaging nine neighboring Z_e–Z_DR data pairs increases the correct identification of the rain type (as determined from the profiler measurements) to about 70%. While some additional averaging improves the effectiveness of the BB and NBB rain type segregation, too much averaging can provide occurrences when measurements from both rain types are present in a same sample of Z_e–Z_DR data.

3.2. Differences in Z_e–R Estimators for Warm and Stratiform Rains

A Parsivel disdrometer was added to the TDE observational site instrumentation suite at a later stage of the deployment. Drop-size distribution data from disdrometer measurements were used for calculating Z_e–R estimators, which are characteristic for observed warm BB and stratiform NBB rains. Figure 4a shows an example of vertically pointing S-Prof measurements during a TDE precipitation event observed on 9 March 2017 at the time when disdrometer measurements were available.

A clear separation of the warm NBB (i.e., approximately between 11:00 and 15:00 UTC) and stratiform BB (i.e., after 15:00 UTC) rain types is obvious from the data in Figure 4a. For this observation event, Z_e–R estimators corresponding to these rain types are shown in Figure 4b. They were derived using disdrometer DSD-based modeling of radar reflectivity and rain rate.

For comparisons, Figure 4b also shows mean Z_e–R estimators for warm and stratiform rain types obtained in [6] using DSD data from the EWN Southeastern United States observational site. It can be seen from Figure 4b that differences in Z_e–R estimators for warm and stratiform rains are more significant than those between relations for the same rain type but from different observational sites. Underestimation of warm rain rates could be about as much as factors of 2 and 3 (for reflectivities of 20 dBZ and 35 DBZ, respectively) if a stratiform rain estimator is used for QPE. Thus, identifying warm NBB rain as a separate precipitation category and applying rain rate estimators, which are appropriate for this category, could lead to improvements in radar-based QPE retrievals.

4. Discussion and Conclusions

Correspondences between radar reflectivity and differential reflectivity values observed in liquid precipitation can effectively be used to differentiate between warm no bright-band and stratiform bright-band rain. The mean S-band Z_DR–Z_e relations for warm and stratiform rain, which were previously found using data through theoretical modeling with observed DSDs and independent information on rain type partitioning, were found to be generally applicable to measurements from the operational NWS polarimetric WSR-88D KRTX system. For both modeling and observational data, differential reflectivity values for warm NBB rain are, on average, by a factor of about 2 smaller (if expressed in decibels) than those for stratiform BB rain (for the same value of reflectivity).

The Z_DR–Z_e relation Equation (5), which approximately represents an average of the theoretically found relations for warm NBB and stratiform BB rains, can be used to segregate these rain types. The segregation method suggests that if the observed differential reflectivity (for a given observed Z_e value) is larger/smaller than that found from the relation Equation (5), then the observed rain type is identified as stratiform BB/warm NBB rain. Convective rain periods in radar observations could be identified [14] prior to applying the method suggested here.

Statistical evaluations of the BB–NBB rain differentiation method were performed on the independent data set consisting of measurements by the operational weather radar when rain types were known from profiler measurements. These evaluations revealed that the suggested method correctly identifies rain type for about 70% of observed Z_DR–Z_e pairs if a differential reflectivity measurement bias in operational weather radar measurements is approximately accounted for and an averaging of reflectivity and differential reflectivity data is performed. This ≈70% effectiveness estimate provides a probabilistic measure to a “binary” decision rule for distinguishing between NBB and BB rain types based on the relation shown in Equation (5). Due to measurement uncertainty of polarimetric radar variables, this effectiveness estimate is smaller than the about 80% efficacy previously found for modeling data.

The fact that Z_DR–Z_e relations, which were found through modeling using DSDs observed during one-year long deployment in the Southeastern United States [6], fit well, on average, the observational data from an operational weather radar on the West Coast of the United States points out to a general robustness of the warm–stratiform rain separation method based on the mean correspondence between reflectivity and differential reflectivity. It also indicates that this method could have a broader potential utility for enhancing radar-based QPE by adding a warm–stratiform rain differentiation in addition to currently existing procedures to itentify convective rain. The suggested here method/approach should be used for rain observations with lowest radar elevation beam measurements that are sufficiently below the environmental freezing level to avoid contaminations by melting and ice hydrometeors. Higher elevation beam measurements are often prone to such contaminations.

Z_e–R estimators for warm NBB rain suggest significantly higher rain rains for the same reflectivity values compared to stratiform BB rains. The variability between warm rain estimators obtained from different DSD datasets is generally smaller than differences between mean warm and stratiform rain estimators. Differentiating warm rain as a separate rain type and applying appropriate rain rate estimators could lead to better radar-based QPE.