Using Sentinel-2 Images to Estimate Topography, Tidal-Stage Lags and Exposure Periods over Large Intertidal Areas

Abstract

Intertidal areas provide key ecosystem services but are declining worldwide. Digital elevation models (DEMs) are important tools to monitor the evolution of such areas. In this study, we aim at (i) estimating the intertidal topography based on an established pixel-wise algorithm, from Sentinel-2 MultiSpectral Instrument scenes, (ii) implementing a set of procedures to improve the quality of such estimation, and (iii) estimating the exposure period of the intertidal area of the Bijagós Archipelago, Guinea-Bissau. We first propose a four-parameter logistic regression to estimate intertidal topography. Afterwards, we develop a novel method to estimate tide-stage lags in the area covered by a Sentinel-2 scene to correct for geographical bias in topographic estimation resulting from differences in water height within each image. Our method searches for the minimum differences in height estimates obtained from rising and ebbing tides separately, enabling the estimation of cotidal lines. Tidal-stage differences estimated closely matched those published by official authorities. We re-estimated pixel heights from which we produced a model of intertidal exposure period. We obtained a high correlation between predicted and in-situ measurements of exposure period. We highlight the importance of remote sensing to deliver large-scale intertidal DEM and tide-stage data, with relevance for coastal safety, ecology and biodiversity conservation.

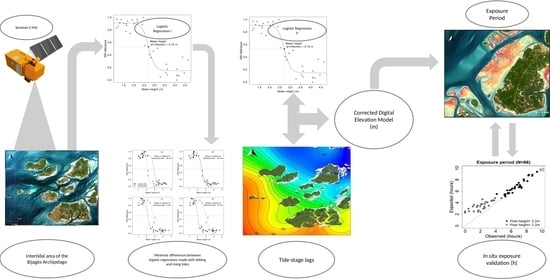
1. Introduction

Intertidal flats represent transitional ecosystems linking marine and terrestrial areas and are characterized by vast extensions of sediments undergoing regular cycles of inundation by seawater and exposure to air [1]. These are very productive areas, intensively used by underwater consumers such as fish during high tide and sustaining a large variety and abundance of air-breeding predators such as shorebirds during low tide. Benthic producers and invertebrates that live in the sediments are pivotal in these ecosystems, as they constitute the main source of food for these two disparate predator assemblages. Intertidal systems and associated margins also provide for key ecosystem services, acting as a nursery and habitat for economically important resources (e.g., crustaceans, molluscs and fishes, [2]), and also contributing to coastal protection, nutrient cycling and carbon storage [3,4]. Still, these ecosystems are threatened at a global scale by land reclamation [5], sediment dredging [6] and sea-level rise [7]. Indeed, a large proportion of the area covered by intertidal systems declined globally by ca. 16% between 1984 and 2016 [7] and 68% of their extent is currently subject to moderate to very high human pressure [8]. Hence, characterizing and monitoring changes in such ecologically valuable systems is a priority in order to delineate more effective conservation actions.

Over the past three decades, several techniques have been used to map intertidal areas and also to develop digital elevation models (DEM) for these areas. Some studies have involved the use of acoustic sounders installed on ships which provide reliable measurements of topography, but these techniques are very expensive and time-consuming when large areas are involved [9]. Airborne Light Detection and Ranging (LIDAR) is a very promising technique, being able to accurately generate bathymetry estimates [10] at depths of up to 70 m in clear water [11]. However, the reliability of such techniques can be affected by water turbidity, and its application is usually constrained to local and regional scales due to very high acquisition costs [12].

Due to these difficulties, intertidal topography remains poorly mapped worldwide [13,14], despite its importance to predict flood impacts and other foreseeable changes on many coastal ecosystems due to sea-level rise [15,16]. In fact, accurately generated DEMs allow for the determination of the coastal slope and for the identification of areas with a low tidal range, which are significant parameters for calculating coastal vulnerability indices, and for the assessment of the impacts of the climate change-induced sea-level rise on these areas [17,18]. DEMs have also other applications, being useful for instance, in estimating inundation/exposure periods of intertidal areas [19]. This is a meaningful exercise from an ecological perspective as one important factor affecting biota zonation in intertidal areas is the exposure period [20,21], an attribute difficult to obtain over large scales by traditional sampling or observation [19].

The “waterline method” constitutes a simple and cost-effective alternative to derive the intertidal topography over large geographic regions [22]. This multi-temporal approach estimates intertidal topography from a set of topographic contours obtained from satellite images, depicting the position of the waterline at the widest possible range of tidal stages [14]. These contours can be assigned to a specific elevation by using hydrodynamic models to calculate the water height at the time of the acquisition of each image. Synthetic Aperture Radar (SAR) or Multispectral Instruments (MSI), such as Sentinel-2 sensors, have been used to this end and may be the only practical way to extract elevation values in remote and inaccessible places [23,24,25]. Recently, the authors of [26] proposed a variation to the waterline method, consisting of a pixel-based technique using the backscatter of a time-series of SAR Sentinel-1 images to generate a DEM of intertidal areas. The technique was later generalized for multispectral images [27]. This technique explores the relationship between the near infrared (NIR) reflectance and pixel elevation, which can be described by a logistic regression, relating a set of values of the water height at the time of image acquisition with the corresponding NIR values of each pixel. In this relationship, NIR reflectance values at a given point will suddenly shift from high values, when the pixel is exposed, to low values, when the pixel is covered by water (which strongly absorbs IR radiation). The water height at this shift point is assumed to represent the height of that particular pixel [26,27].

The application of this method requires precise information concerning the height of the water at the particular time of image acquisition. Such data are often calculated from tidal models developed for a given region, based on longitudinal observations collected by a network of sea-level gauges which are used to derive the regions’ tidal constituents. However, in remote locations the number of available gauges is often very limited and consequently tidal models are unable to capture spatial differences in the stage of the tide over large extents. In such situations, one often assumes that the water height measured at one reference point is the same across the entire region, a simplification that can lead to significant errors in the estimates of elevation values when tide-stage differences are significant [27]. An alternative approach is to use tidal prediction models, such as the Oregon State University Tidal Prediction Software (OTPS) [28], which had been used for continental scale time-series tide modelling [25,29]. However, the accuracy of tide heights estimation again decreases with increasing distances from the gauge location, most particularly in estuarine and insular areas where river flows and landmass configuration can alter tidal currents and cause considerable tide-stage lags [25].

In this study, we propose a set of procedures to address the issues outlined above and further develop the quality of DEM estimation of large intertidal flats using images sensed by Sentinel-2 Multi Spectral Instrument (S2A&B, hereafter). Using a time-series of images of the Bijagós Archipelago off the coast of Guinea-Bissau, West Africa, we (i) propose a four-parameter alternative for the pixel-based logistic algorithm proposed by the authors of [27] to produce a DEM of the intertidal area, and (ii) implement a pre-calibration procedure for all bands of the images in the time-series to reduce temporal variability at the pixel level. Furthermore, we (iii) propose a novel method to estimate cotidal lines in the entire extent of the Sentinel-2 scene and (iv) produce a final DEM of the area, after correcting for differences in tidal-stage across the region. Finally, (v) we use the final DEM to produce a detailed (10 m resolution) map of exposure periods, and (vi) assess the quality of the prediction using measurements of the exposure period made in the field.

2. Materials and Methods

2.1. Study Area

This study took place in the Bijagós Archipelago, located off the coast of Guinea-Bissau (11°52′N, 15°36′W, Figure 1). The archipelago comprises 88 islands and islets, and it is classified as a Biosphere Reserve by UNESCO (2011) and as a Wetland of International Importance under the Ramsar Convention. The total area of this archipelago is ca. 10,470 km², of which 1200 km² are occupied by intertidal mudflats and sandbanks [30] and ca. 650 km² are covered by mangrove forests [31]. The Bijagós Archipelago has a semi-diurnal tide regime, with strongest spring tides ranging from 0.3 m to 4.8 m according to the Portuguese Hydrographic Institute (IH—Instituto Hidrográfico) [32].

2.2. Image Selection and Pre-Processing

A total of 35 Level-1C-processed images from S2A&B were downloaded from Sentinel’s Scientific Data Hub (https://scihub.copernicus.eu/), georeferenced in WGS84/UTM 28 N time zone [33,34] (the specifications of the MultiSpectral Instrument onboard Sentinel-2 can be found at https://sentinel.esa.int/web/sentinel/missions/sentinel-2/instrument-payload/resolution-and-swath). The images were sensed in two different periods: between December 2017 and May 2018 and November 2019 and April 2020 (Table S1, Supplementary Material). In addition to presenting a cloud cover lower than 10%, images were selected to depict the most diverse situations of tidal stages in order to get the most accurate representation of the spatial progression of the water across the intertidal area.

Atmospheric correction is a crucial step in the analysis of multispectral satellite images, namely to improve the accuracy of bathymetric models [23,35,36]. Hence, we converted all Level-1C top of atmosphere reflectance products (ρ_toa) into Level-2A (L2A) bottom of atmosphere surface reflectance products (ρ_s), using the ACOLITE software (version 20190326.0) developed by the Royal Belgian Institute of Natural Sciences (RBINS) [37]. The ACOLITE processor was especially designed for aquatic applications and it uses the “dark spectrum fitting” approach, described in [38,39,40]. For the purposes of this study, we only used the green (560 nm) and NIR (~833 nm) bands as processed by ACOLITE, both at 10 m resolution. All other analyses were carried out in R software v.4.0.0 [41], mostly using the library raster [42] and its dependencies.

Despite this atmospheric correction, scenes from the same area obtained in different dates will often show some differences in the range of band reflectance, even if representing regions that remained almost unchanged. Such differences can result from slight differences in light conditions at the corresponding acquisition dates and can be detected by simply plotting the reflectance of a given band obtained in two different periods for the same area (Figure 2). To calibrate the bands of each scene to a common dynamic range, we used one of the scenes (informally selected to have an average reflectance range in the green and NIR bands) as a reference and then we calculated band-wise major axis regressions with all other images, which were then corrected using the corresponding regression coefficients (Figure 2). Major axis regressions minimize the sum of squared distances between the points and the regression line, measured perpendicularly to the line, and were estimated using lmodel2 package [43] in R software. While fitting these regressions, we only included pixels with very low (<0.05) and high (0.2) NIR reflectance, representing seawater and land areas, respectively, and excluded intertidal areas which vary considerably among scenes, according to the tidal-stage (Figure 2).

2.3. Estimation of Water Heights in Sentinel-2 Scenes

We compiled information on the time of high- and low-water at the Bijagós Archipelago, as well as the corresponding water heights for each scene used in this study, from the Portuguese Hydrographic Institute (https://www.hidrografico.pt/). The data available refer to a single location in the archipelago, Bubaque (Longitude 15°50.0′W; Latitude 11°18.1′N). Based on these values, we estimated the water height at the exact time of image acquisition (hsat) as:

$$h_{sat}=h_{HighWater}-\frac{\left(h_{HighWater}-h_{LowWater}\right)\times \left(cos\left(\pi \times \frac{T_{sat}-T_{LowWater}}{T_{HighWater}-T_{LowWater}}\right)+1\right)}{2}$$

(1)

where h_sat corresponds to the water height predicted at the satellite sensing time (T_sat), in meters (m), h_LowWater and h_HighWater correspond to the low- and high-water marks, respectively, and T_LowWater and T_HighWater to the time of low and high water in hours, respectively (water heights are presented in Table S1, Supplementary Material).

2.4. Identification of the Intertidal Area

The method developed by authors in [27] is computationally intensive, since it requires a set of operations carried out at each pixel of the image. To avoid unnecessary calculations, the process starts by identifying the zone of interest, comprising only pixels in the intertidal area. To achieve this, we first calculated the Normalized Difference Water Index (NDWI, proposed by authors in [44] for each image), to maximize the contrast between water and other land cover types. This index is calculated as a standardized ratio between the green and NIR reflectance ($\rho$), as given by equation:

$$NDWI=\frac{{\rho }_{Green}-{\rho }_{NIR}}{{\rho }_{Green}+{\rho }_{NIR}}$$

(2)

Pixels corresponding to permanent water bodies and to land have a low temporal variability in their NDWI values, since they represent relatively constant conditions. In contrast, pixels in the intertidal zone typically show a higher variability in NDWI, as they are subject to cycles of exposure to air and coverage by water. We followed the authors of [27] to identify areas of land, water and intertidal areas using increasing thresholds of temporal variability in NDWI. Using the NDWI of all scenes, we then calculated the temporal standard deviation in NDWI of each pixel, based on all scenes, as:

$${\sigma }_{\left(x,y\right)}=\sqrt{\frac{1}{M}{\displaystyle \sum _{i=1}^M}{\left(NDW{I}_i-\overline{NDWI}\right)}^2}$$

(3)

where $\overline{NDWI}$ is the temporal mean of the NDWI of each pixel (x, y) across all images (M).

2.5. Estimation of the Height of Intertidal Pixels

The elevation of each pixel can be estimated by the height of the water at which its NIR reflectance suffers a sudden change in magnitude. Emerged areas of the intertidal typically show high NIR reflectance, which will suddenly drop to very low values when the water line reaches that area, due to the high NIR absorption. Therefore, as proposed by [27], one expects a sigmoid relationship between the height of the water and the NIR reflectance of a given pixel, given by:

$${\rho }_{i\left(x,y\right)}=\frac{\left(topasymptote-bottomasymptote\right)}{1+e^{-a\left(h_i-h_{pixel}\right)}}+bottomasymptote,i=1,\dots ,M$$

(4)

where ρ_i is the standardized NIR reflectance of the pixel with coordinates (x, y), h_pixel corresponds to the elevation (in meters) of the pixel (x, y) and h_i is the water height associated with each scene (in meters, Figure 3). Besides the inflection point (h_pixel), which is our main parameter of interest, the logistic function is characterized by three other parameters: top asymptote, bottom asymptote and steepness (a). These four parameters were estimated for each intertidal pixel using the nplr package [45], running in R software [41]. The algorithm uses a Newton-Raphson method to minimize a weighted sum of squared errors [45], and whenever model convergence was not reached, the pixel was marked as being outside of the intertidal zone. This procedure was run for each pixel of the intertidal area, resulting in a preliminary DEM of the archipelago.

2.6. Estimation of Differences in Tidal-Stage across the Archipelago

As mentioned above, the times of high- and low-tides available for the Bijagós Archipelago have been calculated from measurements at a single location, in the Island of Bubaque (see Figure 1). However, the archipelago extends over ca. 100 km in latitude and in longitude, and therefore considerable differences in tidal stages are expected to occur across the region. Such differences will obviously impact the estimation of the heights of each pixel, since the height of the water at a particular location at the time of acquisition of the satellite images (h_i in Equation (4)) will differ from that of the reference location (in Bubaque). The difference between tidal stages will obviously increase with an increasing distance between the locations along the axis of tide-wave progression, introducing a systematic geographic bias in the estimation of intertidal DEM. To account for this problem, we estimated the tide lags for the Bijagós Archipelago by examining the differences between the predictions of pixel height obtained using satellite scenes representing rising tides only, as compared with those obtained with images acquired during ebbing tides. In fact, if the local tidal-stage is correctly determined, the pixel height estimated from images depicting ebbing tides should be fairly similar to that obtained with data representing rising tides. However, if the predicted water height at a given location occurs e.g., 1 h after the reference value used in the model, one would expect that predictions of pixel height based on rising tides will be underestimated (as the water is yet to reach the height required to cover the pixel), while predictions based on ebbing tide deliver overestimated heights (because the water will still be covering that pixel for 1 h, see Figure 4c). Likewise, when the tidal-stage at a place occurs, for example, 1 h before the time in the reference location, the opposite will occur (Figure 4a).

We explored these differences among tide stages to estimate the time-lags of each pixel. To do this, we run two separate logistic models, one based on images representing ebbing tides and another one using rising tides. We then defined a sequence of potential tide time-lags ranging from −90 min to +90 min (at 5 min intervals) in relation to the tidal time of our reference point (at Bubaque), and for each of these values we recalculated the water height of all images within each dataset (one for scenes acquired during ebbing tides and another for rising tides). We fit a set of models for each time-lag and dataset, and finally selected the time-lag that resulted in the smallest difference between the estimated pixel height of ebbing- and rising-tide models (see Figure 5). This computationally intensive procedure was repeated for 50,000 random pixels in the intertidal area, selected among those previously estimated to have an elevation within 2.47 ± 0.25 m (see above). This value corresponds to the mean water height of all satellite images, ensuring that the distribution of points around the inflection point is more balanced and therefore parameter estimation is more accurate.

To estimate the time differences in tidal-stage for all intertidal pixels of our study region, we fit a generalized additive model (GAM) using the time differences in tidal-stage estimated at the 50,000 random pixels as dependent variable and the longitude and latitude as predictors, using mgcv package [46]. GAM fit involved the use of penalized thin-plate regression splines, with regression parameters (i.e., amount of smoothing) selected by generalized cross-validation [46]. We choose this type of model because tide-stage delays are expected to show a very strong spatial (latitudinal and longitudinal) correlation, hence a very smooth spatial variation which will be well captured by the use of thin-plate splines.

2.7. Production of the Final Bathymetric Map

Based on the previous procedure, we produced a map representing the spatial differences in tidal-stage across the archipelago. Using this information, we re-estimated the heights of all intertidal pixels using the logistic function as explained above, but now calculating the water heights of all images according to the time-lag in the tide stage, in relation to the reference point (Bubaque).

2.8. Estimation and Validation of the Intertidal Exposure Period

We used the corrected pixel elevation to estimate the exposure period of all pixels in the intertidal zone, assuming a simple sinusoidal function and a tide cycle lasting 12.40 h. This value corresponds to the mean cycle duration recorded in our Sentinel-2 scenes dataset (mean = 12.40 ± 0.13 h, n = 35 days). We used this value in a simple sinusoidal function to estimate the exposure period (in hours) of each pixel:

$$Exposure\left(h\right)=12.40\times \left(1-\frac{acos\left(2\times \left(\frac{h_{pixel}-h_{LowWater}}{h_{HighWater}-h_{LowWater}}\right)-1\right)}{\pi }\right)$$

(5)

where h_pixel is the height of the pixel (m), and h_HighWater and h_LowWater are the high- and low-water marks (m), respectively. We used this formula to produce a map representing the exposure periods of intertidal sediments for an average tide, using a mean high- and low-water mark of 1.05 m (±0.55 m SD) and 3.90 m (±0.54 m SD), respectively, calculated as averages of the values obtained in the Sentinel-2 scenes dataset (n = 35).

To validate the map of the exposure period, we measured the exposure/inundation periods at 66 sites using time-lapse cameras in different islands of the archipelago. Between February and March 2020, we set several cameras in the intertidal area, fixed them to a stick and facing at its base to record the exact time the water reached each site during ebbing and rising tides (Figure S1 in Supplementary Material). The location of each camera was georeferenced with a portable GPS (ca. 4 m accuracy), and recorded footage at 1-min intervals which were subsequently examined to determine the exposure period of each site. These field measurements were compared with exposure values estimated by the models at the same pixels, as determined by their GPS positions. To calculate the predicted height of each pixel, we used the tide parameters (h_HighWater and h_LowWater) for the corresponding camera sampling dates. A schematic representation of all procedures is presented in Figure 6.

3. Results

3.1. Identification of the Intertidal Area

The inter-calibration of the images was the first step of all the analysis described below and had a visible effect on the dynamic range of the NIR reflectance in our image set (see Figure 2), most especially by reducing the variability at low reflectance levels which in turn affected the pixel height estimation (Figure S2 in Supplementary Material). The distribution of the standard deviations in NDWI calculated for all pixels showed three clear peaks (Figure 7), with the lowest values associated with land (highest stability in NDWI values), and the highest temporal variability associated with intertidal areas. The highest peak, corresponding to areas of water, showed intermediate variability in NDWI. We defined a threshold of SD(NDWI) = 0.2, above which pixels were considered to represent intertidal areas (see Figure S3 in Supplementary Material). This conservative value was defined as to minimize the omission error for pixels in the intertidal area, and any pixel misclassified as water will be excluded in subsequent analytical steps.

3.2. DEM of the Bijagós Archipelago

The automated application of the logistic function (Equation (4)) to each pixel provided a map of the elevation of the intertidal flats of the archipelago with a high spatial detail, capturing the slopes associated with small channels in the intertidal area (Figure 8). The estimated elevation values ranged from 1.04 to 4.69 m, limited by the lowest and highest tides recorded in our scene dataset. According to the Portuguese Hydrographic Institute, the hydrographic reference at Bubaque is 2.54 m below mean sea level.

3.3. Estimation of Spatial Differences in Tidal-Stage at the Archipelago Scale

The representation of differences in tidal-stage across the archipelago is shown in Figure 9. The orientation of the cotidal lines indicates that the tide progresses along a SW-NE axis, and involves a difference of ca. 1 h in the tidal-stage between the most distant regions in that axis. The stage differences provided by the Hydrographic Institute at four locations were relatively close to those estimated by our model (average absolute difference = 6.6 min), with a maximum discrepancy in Abu (Figure 1), where our prediction underestimates the reported tidal stage by 15 min (see Table S2, in Supplementary Material). A final DEM of the archipelago was calculated after correcting the water height of each image and accounting for the spatial differences in the tidal stage (Figure S4, in Supplementary Material).

3.4. Mapping and Validating the Intertidal Exposure Period

Figure 10 represents the exposure period estimated from the DEM, for an average tide in the archipelago (low water mark = 1.05 m, high water mark = 3.9 m, amplitude = 2.85 m). There was a strong agreement between the predicted exposure periods and those measured in the field using time-lapse cameras (r² = 0.94; n = 66, p < 0.001), with low exposure values presenting lower prediction accuracy (Figure 11).

4. Discussion

In this study we present, for the first time, a set of automated remote sensing methods that allow the estimation of tidal-stage lags over large intertidal areas, the production of cotidal lines, and the predictions of the exposure time of intertidal sediments, which were validated by in-situ measurements of the position of the water line. These procedures can significantly increase the quality of intertidal DEM by removing a geographical bias in water level estimation. We also refined and expanded the application of logistic regressions in a time-series of remote sensed images to estimate the topography of intertidal areas, as proposed by [26,27]. These refinements also included a prior inter-calibration of NIR reflectance among all images in the time series, and a more flexible formulation of the logistic function (now with four parameters).

The quality of the topographic predictions of the intertidal areas using our approach is strongly contingent on the availability of time-series images for a given site. The lowest and highest water marks recorded in the series (generally during spring tides) determine the range of height predictions that the models can provide. On the other hand, the availability of images portraying intermediate water heights is critical to reduce the uncertainty associated with the inflection points of the logistic function, which corresponds to the estimate of the height of the pixel. In this study, we used data from 35 Sentinel-2 A&B scenes, almost twice the number previously used to derive the topography in this area [27]. In doing so, we were able to expand the range of tides from 1.39–4.16 m [27] to 1.04–4.69 m, and also to gather more data from intermediate tidal- stages (7 out of 35 images with water heights between 2 and 3 m). We could not find images with tidal heights lower than 1.04 m, thus preventing the identification of the lowest lying intertidal areas, which only occur in the strongest spring tides, exposing sediments at heights of 0.5 to 1.0 m. However, such strong spring tides are rather uncommon, which reduces the limitation of our approach.

The atmospheric correction of multispectral images is an important step prior to image analysis, as aerosols and gases have a strong influence in the nature of signal, particularly in water bodies [47], where they can constitute up to 90% of the signal [48,49]. This is particularly relevant for the method presented here, which relies to a very large extent on the large and rapid change in pixel reflectance in relation to the presence of water. Our study shows that, despite the atmospheric correction implemented by ACOLITE, some discrepancies persisted in the dynamic range of NIR reflectance of images obtained in different dates (see Figure 2). The application of a major axis regression visibly reduced this unwanted source of variability in the NIR values (see Figure 3), ultimately improving the estimation of the inflection point of the logistic function, from which the height of each pixel is calculated. This linear correction is very easy to implement and it is likely to be of use in several other remote sensing techniques involving the use of time-series of satellite images, such as crop monitoring [50] or annual monitoring of tree vitality [51].

Modelling the water level considering the tide-stage lags over large areas generally improves the accuracy of DEMs [52,53]. Some efforts have been developed to address this issue, but they usually involve continental-scale models (e.g., [25]), where the gravitational effects of the moon are much more significant than, e.g., the smaller scale physiography of the coast of land. Furthermore, at a larger scale there is higher availability from tide gauges to help modelling tide-stage differences. In this study we propose a new method to assess spatial differences in tidal-stage at a smaller scale based on the expected differences in pixel-height estimation obtained from using ebbing tides and rising tides separately. Our approach is still based on the NIR reflectivity of each used pixel and requires a single site as a reference height. This new development enables the estimation of cotidal lines from pixel height estimations made in intertidal areas, and such methodology can be applied in other regions whenever tidal areas are distributed more or less evenly across the region of interest. The Bijagós Archipelago represents an almost ideal setting for such application, since there are extensive intertidal areas associated with each island providing a good spatial coverage for tide lag estimation. Cotidal maps are by themselves useful products but are also a significant advance as a means of reducing the geographical bias in techniques that rely on exact water heights registration across the region of interest. This is particularly relevant in remote areas where tide gauges are scarce and, therefore, information on tide stage lags is totally absent.

The estimated cotidal lines for the Bijagós Archipelago indicate a tide progression roughly from SW to NE, being more compressed in areas with higher landmass concentration, and shallower waters both causing a stronger gradient in the tidal wave. The cotidal line corresponding to the absence of tide-stage lag lies very close to the eastern tip of Bubaque (see Figure 8), thus correctly matching the location of the reference tide measurements. This observation, together with the low mean absolute error (6.6 min, see Supplementary Material Table S1), is a good indication of the adequacy of the method, despite the somewhat larger error observed at the northern part of the areas (15 min in relation to the value reported by the Hydrographic Institute). These larger differences might be due to the fact that the reference data provided by IH is probably outdated, as they are based on tidal observations carried out in the 1960s. However, they may also steam from the inability of the method to distinguish between the small discrepancies in tide lags associated with rising and ebbing tides, with spring and neap tides, with shallower and deeper areas, therefore representing average conditions for the region.

To assess the quality of our final DEM, we validated our predictions of exposure periods (produced based on the corrected DEM) with a large set of direct measurements of the waterline position. There was a very good agreement between the observed exposure periods and those predicted by our model. As expected, pixels with lower elevation showed a higher-than-expected exposure period, producing a systematic bias, particularly at heights lower than 2.2 m. To some extent, this can occur because the intertidal sediments are predominantly muddy [27]. In fact, in these areas the intertidal sediments are exposed for only a short period, and therefore often retain a thin film of surface water or form small water pools that never dry completely. This circumstance ultimately affects the NIR reflectance (because NIR radiation is absorbed by this film of water) and results in a slight overestimation of the corresponding bathymetric values. Nonetheless, the final exposure product has a very strong correlation with the observed values showing that, with some subsequent calibration work, the remote sensing approach we present can deliver large scale and very detailed DEMs and average exposure data, with relevance for many areas, from coastal safety to ecology and conservation of these critically important habitats, which are globally threatened due to climate changes [7].

5. Conclusions

The method proposed in this study allows for the estimation of differences in water elevation due to the spatial variation in the tidal phase, using Sentinel-2 scenes. We were able to detect differences of over 1 h in the tide-phase within the Bijagós Archipelago, an area encompassed by a single Sentinel-2 scene. Although this study was carried out with Sentinel-2 scenes, our approach can probably be applied to scenes acquired by other sensors with similar characteristics, including the ones onboard Landsat 8. Landsat 8 scenes have an extent of 170 km by 185 km, and therefore spatial differences in water height are likely to be even more significant. The methodological refinements proposed in the study, and the possibility to correct for differences in tide-phases, allow for important improvements in the accuracy of intertidal DEMs. This is of significant relevance, since these coastal habitats are likely to undergo important topographical changes in the near future due to sediment mobilization caused by sea-level rise and by increased frequency of extreme weather events associated with the ongoing climatic changes. Accurate intertidal maps and DEMs are also an important tool to resource (including wildlife) managers, since the topography influences several important ecosystem processes (e.g., the settlement of specific life-stages of commercially relevant marine organisms), which in turn affects the spatial variation in the structure of communities, from benthic organisms to higher vertebrates.