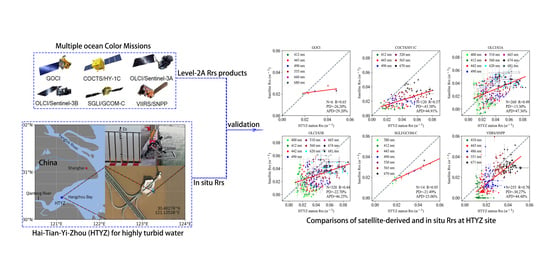
Evaluation of Remote-Sensing Reflectance Products from Multiple Ocean Color Missions in Highly Turbid Water (Hangzhou Bay)

Abstract

Validation of remote-sensing reflectance (Rrs) products is necessary for the quantitative application of ocean color satellite data. While validation of Rrs products has been performed in low to moderate turbidity waters, their performance in highly turbid water remains poorly known. Here, we used in situ Rrs data from Hangzhou Bay (HZB), one of the world’s most turbid estuaries, to evaluate agency-distributed Rrs products for multiple ocean color sensors, including the Geostationary Ocean Color Imager (GOCI), Chinese Ocean Color and Temperature Scanner aboard HaiYang-1C (COCTS/HY1C), Ocean and Land Color Instrument aboard Sentinel-3A and Sentinel-3B, respectively (OLCI/S3A and OLCI/S3B), Second-Generation Global Imager aboard Global Change Observation Mission-Climate (SGLI/GCOM-C), and Visible Infrared Imaging Radiometer Suite aboard the Suomi National Polar-orbiting Partnership satellite (VIIRS/SNPP). Results showed that GOCI and SGLI/GCOM-C had almost no effective Rrs products in the HZB. Among the others four sensors (COCTS/HY1C, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP), VIIRS/SNPP obtained the largest correlation coefficient (R) with a value of 0.7, while OLCI/S3A obtained the best mean percentage differences (PD) with a value of −13.30%. The average absolute percentage difference (APD) values of the four remote sensors are close, all around 45%. In situ Rrs data from the AERONET-OC ARIAKE site were also used to evaluate the satellite-derived Rrs products in moderately turbid coastal water for comparison. Compared with the validation results at HZB, the performances of Rrs from GOCI, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP were much better at the ARIAKE site with the smallest R (0.77) and largest APD (35.38%) for GOCI, and the worst PD for these four sensors was only −13.15%, indicating that the satellite-retrieved Rrs exhibited better performance. In contrast, Rrs from COCTS/HY1C and SGLI/GCOM-C at ARIAKE site was still significantly underestimated, and the R values of the two satellites were not greater than 0.7, and the APD values were greater than 50%. Therefore, the performance of satellite Rrs products degrades significantly in highly turbid waters and needs to be improved for further retrieval of ocean color components.

1. Introduction

Ocean color remote sensing provides abundant data for ocean-based research, but the quality of remote sensing data can be affected by many factors (radiometric accuracy of sensors, vicarious calibration, atmospheric correction, etc.) [1,2], and atmospheric correction is a key procedure in remote sensing of ocean color [3]. The total reflectance (${\rho }_{\mathrm{t}}$) measured at an ocean color sensor can be written as follows [4]:

$${\rho }_{\mathrm{t}}\left(\lambda \right)=t_{\mathrm{v}}{\rho }_{\mathrm{w}}\left(\lambda \right)+{\rho }_{\mathrm{r}}\left(\lambda \right)+\left[{\rho }_{\mathrm{a}}\left(\lambda \right)+{\rho }_{\mathrm{ar}}\left(\lambda \right)\right]$$

(1)

where $t_{\mathrm{v}}$ is the atmospheric diffuse transmittance, ${\rho }_{\mathrm{w}}$ is the desired water-leaving reflectance, ${\rho }_{\mathrm{r}}$ is the Rayleigh reflectance in the absence of aerosol, ${\rho }_{\mathrm{a}}$ is the aerosol reflectance, and ${\rho }_{\mathrm{ar}}$ is the radiance arising from Rayleigh-aerosol multiple-scattering. The $t_{\mathrm{v}}$ and ${\rho }_{\mathrm{r}}\left(\lambda \right)$ can be accurately calculated [5,6], but accurate calculation of ${\rho }_{\mathrm{a}}\left(\lambda \right)+{\rho }_{\mathrm{ar}}\left(\lambda \right)$ is difficult, and small errors will lead to high uncertainty in the ${\rho }_{\mathrm{w}}$.

Generally speaking, the water-leaving radiance from water in the near-infrared (NIR) band of the open ocean is negligible. Gordon and Wang (1994) estimated the aerosol contribution in the NIR bands based on the assumption that the water-leaving radiance of NIR bands is zero, extrapolated the aerosol contribution in other visible-light bands [1], and developed the atmospheric correction algorithm of SeaWiFS for open ocean. While in coastal water, the water-leaving radiance of NIR bands is often not negligible, and it is easily affected by terrestrial pixels [7,8,9]. In addition, the mutual influence of terrestrial-source and marine-source aerosols makes the influence of aerosols on atmospheric correction more complicated [10,11], and the existing aerosol models are not fully applicable [12]. Some atmospheric correction methods for coastal waters based on ultraviolet (UV) band [13,14], shortwave infrared (SWIR) band [15,16,17,18,19], and neural network models [20,21] have been developed.

The uncertainty of satellite data needs to meet the threshold requirements of satellite-based research and applications. Therefore, the performance of remote sensing data must be evaluated using in situ data. Various validations of ocean color remote sensing products have been carried out for different satellite ocean color sensors based on in situ data acquired from cruises, optical buoys [22,23], and fixed stations, such as the AERONET-Ocean Color Network (AERONET-OC) [24,25,26,27,28,29,30,31]. The average of the n × n pixel box can be used to filter sensor and algorithm noise [32]. The sizes of the pixel box include 3 × 3 [33,34,35], 5 × 5 [36,37,38], and 11 × 11 [39], and Pahlevan et al. (2021) chose a fixed real size, and then determined the size of the pixel box was 9 × 9 and 15 × 15 according to the resolution of the satellite [40]. Satellite-derived products over the open ocean have good accuracy [3], but the uncertainties are still large over coastal waters [40,41].

The Geostationary Ocean Color Imager (GOCI), Chinese Ocean Color and Temperature Scanner aboard HaiYang-1C (COCTS/HY1C), Ocean and Land Color Instrument aboard Sentinel-3A and Sentinel-3B, respectively (OLCI/S3A and OLCI/S3B), Second-Generation Global Imager aboard Global Change Observation Mission-Climate (SGLI/GCOM-C), and Visible Infrared Imaging Radiometer Suite aboard the Suomi National Polar-orbiting Partnership satellite (VIIRS/SNPP) are six representative ocean color remote sensors currently in operation. The atmospheric correction algorithms of GOCI [42,43] and COCTS/HY1C [44,45,46,47] are implemented based on the algorithm developed by Gordon and Wang (1994) for SeaWiFS [48], and the estimation of aerosol radiative contribution has been improved for obtain of more accurate satellite products in Case 2 water [45,46,49]. OLCI inherits the advantages of MERIS and also inherits MERIS’s neural network atmospheric correction algorithm for Case 2 water [20,21]. This algorithm combines a bio-optical model and a complex radiative transfer model [50,51,52]. In Case 2 water, both SGLI/GCOM-C [53,54] and VIIRS/SNPP (NOAA) [15,18,55,56] use atmospheric correction algorithms based on the shortwave infrared (SWIR) band to estimate the contribution of aerosols, but in fact SGLI/GCOM-C uses one NIR (865 nm) band and one SWIR (1630 nm) band, while VIIRS/SNPP (NOAA) uses two SWIR bands.

The evaluations of the remote sensing products of GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP have mainly occurred in low to moderate turbidity coastal areas. For example, Ahn et al. (2012) [42], Moon et al. (2012) [57], Huang et al. (2019) [58], Liu et al. (2021) [59], and He et al. (2021) [60] evaluated the performance of normalized water-leaving radiance ($\mathrm{Lwn}$) or remote sensing reflectance (Rrs) products from the GOCI based on in situ data of the East China Sea, Japan/East Sea, and Yellow Sea. Feng et al. (2020) [61] and Du et al. (2021) [62] used neural network algorithms and empirical algorithms based on UV bands to retrieve GOCI’s turbidity, respectively, and GOCI-derived turbidity products were in good agreement with the in situ data. GOCI applies a new algorithm based on the near-infrared band, and the retrieved Rrs products are in good agreement with in situ data in the Western Pacific region [63]. Song et al. (2019) evaluated the alternative calibration coefficient estimation model of COCTS and achieved good results in short-term data verification [64]. Chen et al. (2020) evaluated the Rrs products of COCTS/HY1C using in situ data from the South Pacific Gyre region with good spatial homogeneity and high temporal stability and found that the uncertainty of Rrs products in the blue band was less than 5% [65]. Zibordi et al. (2018) evaluated the $\mathrm{Lwn}$ products of OLCI/S3A using in situ data from AERONET-OC and found systematic underestimation of the satellite $\mathrm{Lwn}$ products in the red and blue bands [66]. Tilstone et al. (2021) evaluated the performance of OLCI/S3A, OLCI/S3B, and VIIRS/SNPP in the Atlantic Ocean and found that both OLCI/S3A and OLCI/S3B underestimated chlorophyll-a (Chl-a), and the trend was greater for OLCI/S3A compared to OLCI/S3B [67]. Research on the consistency of OLCI products and in situ data [68,69,70,71,72,73,74,75,76,77,78], the performance comparison with other sensor’s products [79,80,81,82,83,84,85,86,87,88], and the performance of OLCI products with different retrieval algorithms [80,83,86,89,90,91,92] all reveal the great potential of OLCI. In addition, research on SGLI/GCOM-C has mainly concentrated on cloud and aerosols [93,94,95,96,97,98,99,100], with level-2 ocean color remote sensing products poorly studied [101,102]. In situ hyperspectral radiometric data measured at the Marine Optical Buoy (MOBY) [22] were routinely used to monitor VIIRS ocean color products [36,37,103,104,105,106], and AERONET-OC data were also used for VIIRS ocean color products validation [34,35,36,87,88,107]. Other remote sensor products (such as MODIS, OLCI) were also used to evaluate the performance of VIIRS products. Overall, these validations highlight the potential of satellite ocean color products in the open ocean and shelf waters [108,109]. However, the performance of ocean color products in highly turbid waters remains unknown.

In this study, we used time-series in situ Rrs data from the highly turbid Hangzhou Bay (HZB) to evaluate the performance of Rrs products from the GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP. In Section 2, we provide detailed information on the in situ Rrs data measured in HZB and AERONET-OC station (ARIAKE site) and the satellite-derived Rrs products from multiple ocean color sensors. In Section 3, we provide the validation results of the Rrs products from multiple ocean color sensors in highly turbid waters. In Section 4, we compare and discuss the performance of the Rrs products at HZB and ARIAKE site and in highly and lowly-moderately turbid waters.

2. Data and Methods

2.1. In Situ Rrs Data Measured in HZB

Hangzhou Bay, which narrows from east to west, is part of the Qiantang River estuary, adjacent to the north side of the Yangtze River estuary, as shown in Figure 1. In total, $4.8\times {10}^8 \mathrm{t}·{\mathrm{y}}^{-1}$ of sediment is transported by the Yangtze River each year, some of which enters HZB [110] and $7.6\times {10}^6 \mathrm{t}·{\mathrm{y}}^{-1}$ of sediment is transport by the Qiantang River, which is directly discharged into HZB [111]. The average water depth of HZB is ~10 m, and the submarine topography rises from east to west, with an overall gradient of ~$0.06 \mathrm{m}/\mathrm{km}$ [112]. Narrowing of the bay and uplift of the seabed topography together increase the tidal range as the tide propagates to the top of the bay [112]. Under the influence of sediment input from the two rivers and the strong tides, the concentration of total suspended sediment (TSS) in HZB can reach $5000\mathrm{mg}/\mathrm{L}$, and daily variation amplitude can reach $1000 \mathrm{mg}/\mathrm{L}$ [110,111,113]. Therefore, HZB is an ideal region to examine the performance of ocean color products in highly turbid waters.

A high-frequency water spectrum observation system at Hai-Tian-Yi-Zhou (HTYZ) site (121.12528° E, 30.46278° N) was constructed at the middle of the HZB Bridge, which is 16 and 19 km from the south and north coasts, respectively. Sea surface upward radiance ($L\mathrm{water}$), downward sky radiance ($L\mathrm{sky}$), and downward irradiance ($E_{\mathrm{s}}$) were measured by two hyperspectral radiance sensors and one hyperspectral irradiance sensor (Trios RAMSES), respectively. The azimuth angle for two radiance sensors was fixed about 139.64° (referring to northward), and the observation zenith angles of Lsky and Lwater were 40° and 140° (referring to upward), respectively (Figure 1). The sensors were calibrated before they were put into operation. The operating time of the system was from 07:00 a.m. to 17:00 p.m. local time with a step of 15-min. The measured Spectral data covered wavelengths from 320 to 950 nm with a spectral resolution of 3.3 nm. Finally, Rrs was estimated by:

$$\mathrm{Rrs}=\left(L\mathrm{water}-\mathsf{\rho }\times L\mathrm{sky}\right)/E_{\mathrm{s}}$$

(2)

where ρ is the sea surface reflecting coefficient, with value of 0.028 according to Mobley (1999) [114] and Dai et al., (2015) [115]. During the system operation, we carry out routine maintenance once a month, including data backup, sensor cleaning, and power supply inspection. When the system is running abnormally or there is extreme weather such as typhoons, we carry out special maintenance.

As water spectral measurements can be influenced by platform shadow and sun glint at certain times, quality control of the data was first carried out. As per the methods proposed by Zibordi et al. (1999, 2002, 2004, and 2006) [24,26,27,29] and Dai et al. (2015) [115], several conditions were adopted to select high-quality samples. Firstly, when measured $\mathrm{Rrs}$ is affected by platform shadow, the spectral shape changes rapidly [115], thus abnormally low Rrs spectra were removed. Secondly, we eliminated sun glint coefficients greater than 0.005 [116,117]. Thirdly, $\mathrm{Rrs}$ recorded under cloudy days were removed based on atmospheric diffuse transmittance. Actual atmospheric diffuse transmittance is denoted as $t{\left(\lambda \right)}^{\prime }$ and calculated as $t{\left(\lambda \right)}^{\prime }=E_{\mathrm{s}}\left(\lambda \right)/F_0\left(\lambda \right)\cos \mathsf{\theta }$, where $\mathsf{\theta }$ is the solar zenith angle and $F_0$ is the extraterrestrial solar irradiance. Atmospheric diffuse transmittance under an ideal clear sky (assuming aerosol optical thickness of 0.3 corresponding to high aerosol load case) is denoted as $t\left(\lambda \right)$ and calculated by Gordon’s approximate model [48]. Here, if $t\left(750 \mathrm{nm}\right)$ was less than $t{\left(750 \mathrm{nm}\right)}^{\prime }$, it was considered as non-clear sky and the sample was removed [115]. Fourthly, He et al. (2012) found that $\mathrm{Lwn}$ in highly turbid water is low at the ultraviolet band [13]; thus, here, if $\mathrm{Lwn} \left(350 \mathrm{nm}\right)$ was more than $3 \mathrm{mW}/\left({\mathrm{cm}}^2·\mathsf{\mu }\mathrm{m}·\mathrm{sr}\right)$ the sample was removed [115]. Fifthly, to eliminate samples under weak illumination, we also excluded Rrs data when the sun zenith angle was greater than 70°. We used in situ Rrs data from the HTYZ site from July 2019 to July 2020, except for 20 days in December 2019 when effective data were missing due to abnormal power supply.

2.2. In Situ Rrs Data at ARIAKE Site

AERONET-OC can support satellite ocean color investigations and guarantees the consistency and accuracy of long-term data across sites through unified measurement, single calibration, and uniform processing code [31]. AERONET-OC sampling occurs from 08.00 a.m. to 16.00 p.m. local time, with a sampling interval of half an hour. The AERONET-OC products were converted from $\mathrm{Lwn}$ to Rrs using the formula $\mathrm{Rrs}=\mathrm{Lwn}/F_0$, and the value of $F_0$ was taken from Thuiller et al. (2003) [118].

In this study, in situ OC data retrieved at specific AERONET-OC sites, namely ARIAKE TOWER (ARIAKE site), were used to evaluate the multi-source sensor data. The ARIAKE site (130.27195° E, 33.10362° N) is located in the Ariake Sea of Japan at an elevation of 15 m, about 5 km from the coast of Saga. The average depth of the Ariake Sea is 15 m [119]. At this depth the contribution of sea bottom reflection to the Rrs of the water surface is negligible [120]. The station started to provide data in February 2018. It is managed and operated by Saga University. The average annual total suspended sediment (TSS) value at the ARIAKE site is 3.92 $\mathrm{mg}/\mathrm{L}$ (calculated using GOCI’s TSS product from July 2019 to July 2020), which means that the optical properties of the water near the ARIAKE site are complex. In this study, Version 3 Level 1.5 $\mathrm{Lwn}\_\mathrm{IOP}$ data from ARIAKE from July 2019 to July 2020 were used.

2.3. Satellite Data

According to the operating time of the two in situ sites (HTYZ and ARIAKE), we obtained the Level-2A Rrs products from multiple satellite ocean color sensors. Specifically, GOCI Level-2A Rrs products at three noontime observations (11:28, 12:28, and 13:28 Beijing time) were obtained from the Korea Ocean Satellite Center, with six visible light wavelength bands (412, 443, 490, 555, 660, and 680 nm) and a spatial resolution of ~500 m. The COCTS/HY1C Level-2A Rrs products were obtained from the National Satellite Oceanic Application Center of China, with six visible light wavelength bands (412, 443, 490, 520, 565, and 670 nm) and a spatial resolution of ~1.1 km. The full resolution (FR, 300 m) Level-2 Rrs products of OLCI/S3A and OLCI/S3B were obtained from the European Organization for the Exploitation of Meteorological Satellites (EUMETSAT), with 10 visible light wavelength bands (400, 412, 442, 490, 510, 560, 620, 665, 673, and 681 nm). OLCI uses the Baseline Atmospheric Correction (BAC) algorithm inherited from MERIS in Case-1 water and the Alternative Atmospheric Correction (AAC) algorithm for turbid and highly absorbing Case-2 water [20,21,121,122,123]. We obtained the L2-NWLR products of SGLI/GCOM-C from the Japan Aerospace Exploration Agency (JAXA), with seven visible light wavelength bands (380, 412, 443, 490, 530, 565, and 670 nm) and a spatial resolution of 250 m. The Level-2 products of VIIRS/SNPP were obtained from the National Oceanic and Atmospheric Administration (NOAA), which uses the Multi-Sensor Level-1 to Level-2 processing system (MSL12) as an atmospheric correction algorithm. The VIIRS/SNPP has five visible light wavelength bands (410, 443, 486, 551, and 671 nm) and a spatial resolution of 750 m.

2.4. Matchup between Satellite and In Situ Rrs Data

A temporal window of ±30 minutes was used to match the satellite and in situ Rrs data at the HTYZ site due to the strong hydrodynamics at this site [110]. At the ARIAKE site, we adopted a ±1 h temporal window due to the lower hydrodynamics at this site [107].

For spatial matchup between the satellite and in situ Rrs data, average satellite Rrs in a 5 × 5 pixels box centered on the site was used to match the in situ Rrs, except for OLCI/S3A, OLCI/S3B, and SGLI/GCOM-C at HTYZ site. Because the two OLCI sensors and SGLI/GCOM-C have a high spatial resolution, their Rrs products at the HTYZ site could be significantly affected by the platform, thus we shifted the matchup box by four pixels to the northeast. We used several criteria to determine the representativeness of the matchups [27,31]. Specifically, if the number of pixels with effective Rrs in the box was less than half of the total pixel number in the box, then the sample was discarded. Moreover, the coefficient of variation ($\mathrm{CV}=\mathsf{\sigma }/\mathsf{\mu }$, where $\mathsf{\sigma }$ and $\mathsf{\mu }$ are the standard deviation and mean values of Rrs in the box, respectively) was adopted to examine spatial homogeneity in the box [124]. If the CV was larger than 0.4, then the sample was discarded. If a satellite Rrs spectrum with all visible bands met the above spatial quality control conditions, it was considered to be an effective spectrum.

In addition to the spatiotemporal matchups, spectral matchups were also considered. The HTYZ site provides hyperspectral Rrs data from 320–950 nm, which matched all visible light wavelength bands of all six satellite sensors. However, the ARIAKE site only provides in situ Rrs data at eight bands (400–667 nm), and thus did not match all bands of the satellite sensors. We ignored wavelength differences if the center wavelengths between the satellite and in situ bands were less than 5 nm. For cases where the wavelength difference was greater than 5 nm and the wavelength of the satellite sensor band was within the in situ wavelength range (400–667 nm), we estimated the Rrs for the satellite sensor band by interpolating the in situ Rrs, otherwise there was no matchup (resulting in no effective matchups for SGLI/GCOM-C 380 nm, OLCI 681 nm, and GOCI 680 nm at the ARIAKE site). The number of all effective spectra and matchups by each remote sensor at HTYZ site and ARIAKE site are shown in

Table 1. The number of all effective spectra and matchups by each remote sensor at HTYZ site and ARIAKE site.

	GOCI	COCTS/HY1C	OLCI/S3A	OLCI/S3B	SGLI/GCOM-C	VIIRS/SNPP
HTYZ	10/1	38/20	72/26	76/32	7/2	80/51
ARIAKE	392/154	58/27	72/22	77/29	82/30	163/48

Num1/Num2, where Num1 is all effective spectral number of remote sensor and Num2 is number of matchups.

.

2.5. Evaluation Methods

Based on the matchup samples, statistical analyses were carried out to evaluate the performance of the satellite Rrs using liner regression analysis. Specifically, average percentage difference (PD) and absolute percentage difference (APD) were calculated using:

$$\begin{gathered} \mathrm{PD}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\frac{y_i-x_i}{x_i}\times 100\% \\ \mathrm{APD}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\frac{\left|y_i-x_i\right|}{x_i}\times 100\% \end{gathered}$$

(3)

where $x_i$ and $y_i$ represent the in situ and satellite Rrs data, respectively, for a specific matchup sample. Clearly, PD represents bias between satellite and in situ data. A positive PD represents overestimation of the satellite Rrs data compared with the in situ data; a negative PD represents underestimation. In this paper, two standard deviation filtering procedures were applied to ensure that the statistical results obtained from the overall matchups were not skewed by a few extreme abnormal cases. Specifically, any matchups with ${\mathrm{APD}}_{\mathrm{i}}$ values greater than ${\mathsf{\mu }}_{\mathrm{APD}}+2{\mathsf{\sigma }}_{\mathrm{APD}}$, where ${\mathsf{\mu }}_{\mathrm{APD}}$ and ${\mathsf{\sigma }}_{\mathrm{APD}}$ represent initial average and standard deviation of all matchups, respectively, were excluded from matchup comparison analysis [27,107].

3. Results

3.1. Analysis of Spectral Consistency

Figure 2 shows the spectral comparisons among all effective satellite-derived Rrs from GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, and SGLI/GCOM-C and in situ Rrs at the HTYZ site. In total, we identified 1509 effective samples of Rrs at HTYZ, and 10, 38, 72, 76, 7, and 80 effective Rrs samples for GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP, respectively. The average curve of the in situ Rrs increased with the increase in wavelength from 380–670 nm. After a peak at 670 nm, Rrs decreased slightly with the increase in wavelength. Overall, the spectral shape of the satellite-derived Rrs was consistent with the in situ average Rrs, which peaked at 670 nm, except for the average Rrs of GOCI with a peak value at 555 nm. In terms of magnitude, the Rrs from in situ, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP at HTYZ ranged from $0.005-0.09{ \mathrm{sr}}^{-1}$, $0.023-0.050{ \mathrm{sr}}^{-1}$, $0.03-0.058{ \mathrm{sr}}^{-1}$, $0.02-0.068 {\mathrm{sr}}^{-1}$, $0.015-0.037{ \mathrm{sr}}^{-1}$, and $0.02-0.05{ \mathrm{sr}}^{-1}$ at 670 nm, respectively. It should be noted that the Rrs from OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP had negative values at the blue band (412 nm), which was likely caused by the overestimation of aerosol scattering radiance in atmospheric correction.

Further comparisons of satellite and in situ Rrs data for each sensor are shown in Figure 3. When the wavelength was less than 555 nm, the average Rrs of the GOCI and in situ data showed similar increasing trends as wavelength increased, though their differences also increased significantly as wavelength increased. However, when the wavelength was greater than 555 nm, average GOCI Rrs was inconsistent with the in situ Rrs spectrum, and the Rrs values by GOCI were significantly underestimated. The spectral shape of the average COCTS/HY1C Rrs was consistent with the in situ data, however COCTS/HY1C systematically underestimated Rrs. The average Rrs spectra of OLCI/S3A and OLCI/S3B were slightly lower than that of the in situ data. It should be noted that the performances of OLCI/S3A and OLCI/S3B were not identical. The σ values of OLCI/S3A decreased with increasing wavelength, while the σ values of OLCI/S3B hardly changed. As seen in Figure 2 and Figure 3, the differences in average Rrs between OLCI/S3A and OLCI/S3B were most obvious at 681 nm. The average Rrs values of VIIRS/SNPP and SGLI/GCOM-C were lower than the in situ data in all bands. Although the average Rrs values of VIIRS/SNPP and SGLI/GCOM-C increased with wavelength, like the in situ data, the growth rate of the satellite-derived Rrs decreased significantly after 565 nm. Therefore, in the long-wavelength bands, the differences between the satellite (VIIRS/SNPP and SGLI/GCOM-C) and in situ Rrs values were greater.

3.2. Time-Series Comparisons

As band settings of the different satellites are not completely consistent, we found several differences in the bands of different satellites in time-series analysis. At the HTYZ site with ultra-high turbidity, the Rrs value increased with increasing wavelength, so the minimum and maximum values were obtained at violet and red bands, respectively, and the increasing trend in Rrs changed ~560 nm. Thus, assessment of seasonal variations in the Rrs(λ) data can be determined using these bands. Therefore, we selected remote sensor bands at 412, 560, and 670 nm at the HTYZ sites.

Figure 4 shows the time-series comparison of Rrs values between the satellite-derived and in situ (HTYZ) data. Due to the high turbidity at HTYZ, only 10 effective Rrs records were available from GOCI in a year and had only seven effective Rrs records were available from SGLI/GCOM-C in a year (effective Rrs spectra were obtained in the summer when water was relatively clean). The remaining four sensors obtained better Rrs records at HTYZ, but the satellite-derived Rrs data were significantly lower than the in situ data. In addition, the in situ Rrs data showed significant seasonal changes, with high values in winter and low values in summer. However, the satellite-derived Rrs data showed no such variation.

3.3. Scatter Plot Comparisons at HTYZ Site

Figure 5 shows scatter-plot comparisons between satellite-derived and HTYZ in situ Rrs data for the six sensors (GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP) with all bands together. We found only one matchup between the GOCI and in situ data, and only two matchups between the SGLI/GCOM-C and in situ data at HTYZ, and thus comparisons were not applicable for these two sensors. However, we found 20, 26, 32, and 51 matchups for COCTS/HY1C, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP, respectively (

Table 2. Statistical results for the comparisons between satellite-derived and in situ Rrs at HTYZ.

COCTS/HY1C	Wavelength (nm)										Total
	412		443		490	520	565		670
N	20		20		20	20	20		20		120
R	−0.14		−0.21		−0.26	−0.36	−0.52		−0.33		0.57
PD (%)	−49.33		−51.17		−46.69	−37.75	−38.72		−36.63		−43.38
APD (%)	54.09		53.68		47.26	39.06	38.72		36.63		44.91
OLCI/S3A	Wavelength (nm)										Total
	400	412	442	490	510	560	620	665	674	681
N	26	26	26	26	26	26	26	26	26	26	260
R	−0.31	−0.3	−0.27	−0.26	−0.25	−0.24	−0.30	−0.31	−0.32	−0.33	0.49
PD (%)	−1.24	−9.99	−13.07	−15.59	−15.75	−15.62	−15.78	−15.43	−15.41	−15.09	−13.30
APD (%)	93.40	83.54	63.71	48.22	43.28	32.35	27.79	27.27	27.06	27.00	47.36
OLCI/S3B	Wavelength (nm)										Total
	400	412	442	490	510	560	620	665	674	681
N	32	32	32	32	32	32	32	32	32	32	320
R	−0.36	−0.38	−0.31	−0.29	−0.28	−0.29	−0.30	−0.28	−0.28	−0.28	0.45
PD (%)	−19.40	−17.50	−24.05	−26.13	−25.63	−23.63	−22.64	−22.23	−22.21	−22.25	−22.57
APD (%)	75.27	68.65	56.15	47.07	43.83	37.28	33.69	33.43	33.01	32.79	46.12
VIIRS/SNPP	Wavelength (nm)										Total
	410		443		486		551		671
N	51		51		51		51		51		255
R	−0.26		−0.27		−0.2		−0.09		0.04		0.70
PD (%)	−57.66		−37.92		−24.66		−7.33		−23.75		−30.27
APD (%)	81.32		54.63		38.92		21.38		26.16		44.48

). Overall, satellite-derived Rrs values showed a significant underestimation with the increase in in situ Rrs values.

The regression lines of COCTS/HY1C, OLCI/S3A, and OLCI/S3B also showed a significant underestimation compared to the in situ data. With the increase in in situ Rrs values, the underestimation of satellite-derived Rrs increased significantly. VIIRS/SNPP also showed systematic underestimation compared to the in situ data, but the increase in underestimation was not obvious.

The correlation coefficients (R) of COCTS/HY1C, OLCI/S3A, OLCI/S3B, VIIRS/SNPP, and HTYZ (in situ) data were 0.57, 0.49, 0.45, and 0.70 for all bands, respectively (Figure 5). The VIIRS/SNPP Rrs showed the highest R value. All single-band R values for COCTS/HY1C were negative (Table 2). All single-band R values for the two OLCI sensors were negative, though the values of OLCI/S3A were greater than that of OLCI/S3B for all bands less than 620 nm, while the R values of OLCI/S3B were greater than that of OLCI/S3A for all bands greater than 620 nm (Table 2). The single-band R values of VIIRS/SNPP were positive at 671 nm (but <0.1) but negative at all other bands (Table 2). These negative and low positive R values indicate poor performance of the satellite-derived Rrs in highly turbid waters.

The average PDs of COCTS/HY1C, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP were −43.38%, −13.30%, −22.57%, and −30.27%, respectively, indicating an underestimation of Rrs for all four sensors. The average APDs of COCTS/HY1C, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP were 44.91%, 47.36%, 46.12%, and 44.48%, respectively, indicating poor consistency between the satellite-derived and in situ Rrs. The single-band APDs of the four remote sensors were larger in the short-wavelength bands and smaller in the long-wavelength bands. At wavelengths $\le 490 \mathrm{nm}$, the single-band APD of OLCI/S3A was greater than that of OLCI/S3B, and at wavelengths $\ge 510 \mathrm{nm}$, the single-band APD of OLCI/S3B was greater than that of OLCI/S3A, indicating that the performance of the two OLCI sensors was inconsistent.

4. Discussion

4.1. Variation in APD with Water Turbidity

In this study, in situ Rrs values in the red-light wavelength band (670 nm) were used to characterize water turbidity and examine the performance of multi-sensor Rrs products under different turbidities, as shown in Figure 6. Overall, the APD values at 412, 443, 490, and 670 nm from VIIRS/SNPP and COCTS/HY1C increased rapidly with increasing water turbidity, indicating the degradation of Rrs product performance for these two sensors with increasing turbidity. Moreover, VIIRS/SNPP did not obtain effective data when Rrs (670 nm) was larger than 0.055 ${\mathrm{sr}}^{-1}$, whereas COCTS/HY1C, OLCI/S3A, and OLCI/S3B obtained effective Rrs data, even Rrs values (670 nm) up to 0.08 ${\mathrm{sr}}^{-1}$.

When the in situ Rrs (670 nm) was less than 0.055 ${\mathrm{sr}}^{-1}$, all four remote sensors obtained effective matchups (Figure 7). Compared with Figure 5, the overall statistical results for the four common bands among sensors showed that VIIRS/SNPP had systematic underestimation with PD value of −36.00%, while there was overestimation with PD values of 4.55% and 26.72% for the OLCI/S3A and OLCI/S3B, respectively. The APD values were comparable with values of 50.26%, 56.73%, and 48.92% for the VIIRS/SNPP, OLCI/S3A, and OLCI/S3B, respectively. Due to only having eight matchups, it is hard to objectively evaluate the performance of COCTS/HYIC when Rrs (670 nm) is less than 0.055 ${\mathrm{sr}}^{-1}$ at HTYZ site.

When the in situ Rrs (670 nm) is greater than 0.055 ${\mathrm{sr}}^{-1}$, only COCTS/HY1C, OLCI/S3A, and OLCI/S3B obtain effective matchups (Figure 8), with PD values of −60.00%, −38.14%, −52.17%, and APD values of 60.00%, 54.14%, and 52.78%, respectively. Compared with Figure 5, the underestimation of all the three sensors has increased. Specifically, the underestimation of COCTS/HY1C has increased significantly; in contrast, the underestimation of the two OLCIs has increased slightly. Overall, none of the four sensors can accurately retrieve the water spectrum in the HZB.

For the 412, 443, and 490 nm bands, with increasing water turbidity, the APD values for OLCI/S3A and OLCI/S3B increased at first, then showed a decreasing trend to a minimum value, and then increased again. Considering that neural network atmospheric correction algorithm is a non-linear algorithm, the change trend of OLCI’s APD may be caused by atmospheric correction. The neural network atmospheric correction model of OLCI is based on the simulated data generated by HYDROLIGHT radiative transfer code plus a bio-optical model relating scattering and absorption coefficients to material concentrations [20,50,51]. The data of water optical properties are mainly from cruises in the North Sea, partly in the Baltic Sea, Mediterranean Sea, and North Atlantic [20,50,51]. These optical properties may not fully cover the water optical types in the Hangzhou Bay with extreme turbidity. Thus, the Rrs products of OLCI/S3A and OLCI/S3B may have higher accuracy under certain water turbidity. At the 670 nm band, the APD values of all four sensors increased with increasing water turbidity.

4.2. Different Performances in High and Moderate Turbidity Waters

As a comparison, we used the in situ Rrs data from the ARIAKE site to examine the performance of the Rrs products from the multiple sensors under moderately turbid water. Figure 9 shows the average Rrs spectrum comparison between the satellite-derived and in situ Rrs at the ARIAKE site. The numbers of the effective Rrs samples from in situ measurement, GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP were 282, 392, 58, 72, 77, 82, and 163, respectively. Overall, the spectrum shape of Rrs derived by all six sensors was consistent with that of the in situ data. The OLCI/S3A, OLCI/S3B, and VIIRS/SNPP data were the closest to the in situ data in both spectral shape and magnitude. Of note, GOCI underestimated Rrs at 555 nm, and SGLI/GCOM-C and COCTS/HY1C underestimated Rrs at all bands. In addition, COCTS/HY1C showed slight deviation in spectral shape, with two peaks at 490 and 565 nm.

In contrast to obtaining almost no effective Rrs data at the highly turbid HTYZ site, GOCI and SGLI/GCOM-C obtained more effective Rrs data at the ARIAKE station, despite significant underestimation. COCTS/HY1C also showed significant underestimation at HTYZ and ARIAKE, and the differences between the COCTS/HY1C and in situ data at ARIAKE were relatively larger at the short-wavelength bands (<565 nm). Similar to the results for HTYZ site, the performances of OLCI/S3A and OLCI/S3B at ARIAKE were also slightly different. The OLCI/S3A data were slightly lower than the in situ data, while the OLCI/S3B data were closer to the in situ data. Overall, the difference in σ between OLCI/S3A and OLCI/S3B at ARIAKE was significantly smaller than the difference at HTYZ. The average Rrs value of SGLI/GCOM-C was markedly lower than the in situ value, even under the moderately turbid waters at ARIAKE. Compared to the significant underestimation at HTYZ, the average Rrs value of VIIRS/SNPP at ARIAKE matched the in situ data quite well.

Figure 10 shows the comparisons between satellite-derived and in situ Rrs data for each sensor at ARIAKE. The number of matchups between satellite-derived and in situ Rrs data at ARIAKE was 154, 27, 22, 29, 30, and 48 for the GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP, respectively (

Table 3. Summary of statistical estimators for the comparisons between all six satellites and ARIAKE.

GOCI	Wavelength (nm)								Total
	412	443	490		555		660
N	154	154	154		154		154		770
R	0.11	0.4	0.65		0.8		0.9		0.77
PD (%)	64.64	23.61	1.18		–18.53		–6.01		12.98
APD (%)	72.72	40.69	22.31		21.17		20.04		35.38
COCTS/HY1C	Wavelength (nm)								Total
	412	443	490		520	565	670
N	27	27	27		27	27	27		162
R	0.28	0.31	0.38		0.43	0.48	0.44		0.70
PD (%)	−53.22	−45.11	−29.49		−16.79	−23.24	−49.89		−36.29
APD (%)	83.98	65.71	39.47		28.40	27.15	63.33		51.34
OLCI/S3A	Wavelength (nm)								Total
	400	412	442	490	510	560	620	665
N	22	22	22	22	22	22	22	22	176
R	0.28	0.35	0.57	0.81	0.86	0.91	0.89	0.86	0.87
PD (%)	−17.16	−46.82	−23.71	−6.52	−6.42	−2.94	1.61	−3.23	−13.15
APD (%)	59.10	58.99	34.86	16.47	12.78	8.44	13.27	19.02	27.87
OLCI/S3B	Wavelength (nm)								Total
	400	412	442	490	510	560	620	665
N	29	29	29	29	29	29	29	29	232
R	0.19	0.29	0.59	0.77	0.76	0.73	0.76	0.79	0.83
PD (%)	−8.79	−13.71	−4.72	2.58	−2.41	−1.12	2.33	−3.42	−3.66
APD (%)	75.38	51.39	33.96	18.67	15.63	10.87	19.70	23.04	31.08
SGLI/GCOM-C	Wavelength (nm)								Total
	412	443	490		530	565	670
N	30	30	30		30	30	30		180
R	0	0.06	0.23		0.35	0.43	0.51		0.62
PD (%)	−77.45	−48.88	−25.50		−26.07	−20.84	−9.19		−34.65
APD (%)	108.61	77.85	46.51		37.32	30.92	42.52		57.29
VIIRS/SNPP	Wavelength (nm)								Total
	410	443	486		551		671
N	48	48	48		48		48		240
R	0.03	0.49	0.72		0.76		0.85		0.87
PD (%)	−42.20	−12.46	−1.34		7.52		−9.71		−11.64
APD (%)	56.41	28.95	17.43		14.62		24.29		28.34

). Overall, when the in situ Rrs was less than 0.007 ${\mathrm{sr}}^{-1}$, GOCI overestimated Rrs values, or else, it underestimated Rrs values. COCTS/HY1C and SGLI/GCOM-C were systematically lower than the in situ data. In contrast, the Rrs values of OLCI/S3A, OLCI/S3B, and VIIRS/SNPP were relatively consistent with the in situ data, thus showing much better performance than that at the HTYZ site.

Table 3 shows the performances of the multi-sensors at the ARIAKE site. The R values for OLCI/S3A, OLCI/S3B, and VIIRS/SNPP (all bands) were greater than 0.80 and much higher than the values at HTYZ (0.49, 0.45, and 0.70, respectively). Similarly, the R value for COCTS/HY1C was 0.70 at ARIAKE, which was much higher than that at HTYZ.

At HTYZ, the R values for each band were mostly negative. In contrast, the R values for each band at ARIAKE were all positive. Except for COCTS/HY1C and SGLI/GCOM-C, the R values of the other four sensors in the red band at ARIAKE were greater than 0.7 (Table 3).

The PD values for GOCI, COCTS/HY1C, OLCI/S3A, OLCI/S3B, SGLI/GCOM-C, and VIIRS/SNPP (all bands) were 12.98%, −36.29%, −13.15%, −3.66%, −34.65%, and −11.64%, respectively, indicating the overestimation by the GOCI while the underestimation by other sensors. In terms of the PD values at each band, GOCI significantly overestimated Rrs values at 412 nm (PD = 64.64%) and 443 nm (PD = 23.61%), while significantly underestimated Rrs at 555 nm (PD = −18.53%). COCTS/HY1C significantly underestimated Rrs values at all bands at both the HTYZ and ARIAKE sites. The PD values for OLCI/S3A at ARIAKE and HTYZ were very close. Unlike the significant underestimation at HTYZ, at the ARIAKE site, the PD value for each band of OLCI/S3B (except 443 nm), whether positive or negative, was relatively close to 0, and the PD value for all bands together was only −3.66%. SGLI/GCOM-C obtained limited valid data at HTYZ, and all bands at ARIAKE were significantly underestimated (total PD of −44.15%). The PD values of VIIRS/SNPP at HTYZ and ARIAKE were −30.27% and −11.64%, respectively, with the underestimation being much smaller at ARIAKE (Table 3).

The APD values for GOCI and SGLI/GCOM-C (all bands) were 35.38% and 57.29%, respectively (Table 3), indicating poor consistency between the satellite-derived and in situ Rrs. At ARIAKE, the consistency between the COCTS/HY1C (APD = 51.34%) and in situ data was poor, similar to that observed at the HTYZ site. At ARIAKE, the APD values of OLCI/S3A, OLCI/S3B, and VIIRS/SNPP were 27.87%, 31.08%, and 28.34%, respectively, which were much better than the APD values at HTYZ (47.36%, 46.12%, and 44.48%, respectively).

The comparison of the scatter points of the four common bands shared by the multi-source remote sensor was shown in Figure 11. Compared with the total PD and APD of all bands as shown in Figure 10, the PD and APD of all four common bands slightly increased. The statistical results showed that the accuracy of OLCI/S3A, OLCI/S3B, and VIIRS/SNPP were close (APD are 32.33%, 31.76%, and 31.77%, respectively). The deviation of OLCI/S3B (PD = −4.82%) was the smallest, and the deviation of OLCI/S3A (PD = −20.07%) was slightly higher than that of VIIRS/SNPP (PD = −16.43%). At ARIAKE site, the statistical results of four common bands were slightly different from that of all bands. However, at the HTYZ site, the total statistical values of the four common bands were quite different from the statistical values of all bands. This means that in moderately turbid water, the various bands of the multi-source sensors can capture the water spectrum well.

In summary, at ARIAKE site, GOCI significantly overestimated Rrs at 410 and 443 nm, and even though it underestimated Rrs at the long-wavelength (>443 nm) bands, the overall PD value indicated overestimation. In addition, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP showed relatively low R values at the short-wavelength (<486 nm) bands, but overall performance was good. COCTS/HY1C and SGLI/GCOM-C significantly underestimated Rrs at all bands. OLCI/S3A performed better than OLCI/S3B at HTYZ, while OLCI/S3B had a smaller deviation and showed better performance than OLCI/S3A at ARIAKE.

4.3. Analysis of Possible Reasons for the Performance of Multi-Source Remote Sensing Products at HTYZ Site

Most of the GOCI Rrs products released by KOSC are masked in the Hangzhou Bay. The atmospheric correction method for GOCI in turbid waters uses adjacent non-turbid water to obtain water-leaving reflectance in the red-light band [125], and then uses empirical relationships between NIR band and red-light band to obtain water-leaving reflectance at the NIR bands as [126]:

$$p_{\mathrm{w}}\left(745\right) = {\displaystyle \sum }_{\mathrm{n}=0}^5{j}_{\mathrm{n}}{\rho }_{\mathrm{w}}{\left(660\right)}^{\mathrm{n}}, p_{\mathrm{w}}\left(865\right) = {\displaystyle \sum }_{\mathrm{n}=1}^2{k}_{\mathrm{n}}{\rho }_{\mathrm{w}}{\left(745\right)}^{\mathrm{n}}$$

where $p_{\mathrm{w}}\left(745\right)$, $p_{\mathrm{w}}\left(660\right)$, and $p_{\mathrm{w}}\left(865\right)$ are the water-leaving reflectance at 745, 660, 865 nm respectively, and $j_{\mathrm{n}}$ and $k_{\mathrm{n}}$ are empirical coefficients. This empirical relationship is only applicable to waters with TSS less than 200 $\mathrm{mg}/\mathrm{L}$ [126], while the TSS concentration in HZB is as higher as 5000 $\mathrm{mg}/\mathrm{L}$ [127], which may cause the failure of GOCI Rrs products in Hangzhou Bay. Similar to GOCI, COCTS/HY1C has no SWIR band and its atmospheric correction adopts the framework of Gordon and Wang (1994) [48,108,128], and the overestimation of the aerosol contribution of NIR bands may be the reason for its poor performance at HTYZ site.

The neural network atmospheric correction model of OLCI in turbid waters is based on the simulated data generated by HYDROLIGHT radiative transfer code plus a bio-optical model relating scattering and absorption coefficients of material concentrations [20,50,51]. The data of water optical properties are mainly from cruises in the North Sea, partly in the Baltic Sea, Mediterranean Sea, and North Atlantic [20,50,51]. These optical properties may not fully cover the water optical types in the Hangzhou Bay with extreme turbidity.

It is well known that atmospheric correction based on SWIR band can improve the performance of remote sensing products in turbid waters [40]. SGLI/GCOM-C’s SWIR-algorithm uses one NIR band (865 nm) and one SWIR band (1630 nm) to estimate the aerosols scattering radiance, but the water-leaving reflectance, in HZB, at 865 nm of is still not negligible [129]. As a result, the aerosol contribution may be overestimated, which led to an underestimation of water-leaving reflectance. VIIRS/SNPP uses SWIR bands of 1238 and 1601 nm to fulfil atmospheric correction in turbid waters [130]. Similarly, in HZB, due to the non-negligible water-leaving radiance at the 1238 nm [129], the aerosol contribution can also be overestimated. Another possible reason is that the use of SWIR bands for atmospheric correction increases noise errors [63,131]. This phenomenon is more obvious in the blue band that is farther from the SWIR band.

Therefore, atmospheric correction algorithms for highly turbid waters should be developed further. In highly turbid waters, water-leaving radiance at ultraviolet (UV) band might much less than that at the visible-light (VIS) bands or even the NIR bands [13,110]. Therefore, the UV band can be used to estimate aerosol scattering radiance in such cases [13]. Although GOCI and COCTS/HY1C do not have UV band, it is still feasible to use the 412 nm band instead of the UV band [13,110]. Singh et al. (2019) proposed an atmospheric correction algorithm based on a combination of UV band (387 nm), blue-light band (443 nm), and NIR bands (named as UVNIR-ex), and obtained a good performance in the Yangtze River Estuary [14]. Therefore, in extremely turbid water, for remote sensors without SWIR bands, such as GOCI and COCTS/HY1C, an atmospheric correction algorithm based on the UV band is an option. Hieronymi et al. (2017) proposed an algorithm consisting of several blended neural networks that were specialized for 13 different optical water classes, and the maximum concentration of inorganic suspended matter was up to 1500 $\mathrm{mg}/\mathrm{L}$ [91]. If the in situ data of water types like HZB are also added to the neural network model training, the atmospheric correction in extremely turbid water may achieve better performance. In addition, in high turbid water, since water-leaving radiance at 1240 nm is still not negligible [129], using longer wavelength SWIR bands combination, such as 1635–2209 nm and 1601–2257 nm may improve the performance of atmospheric correction for SGLI/GCOM-C and VIIRS/SNPP. However, considering that the extrapolation from SWIR band to VIS band is too far, resulting in increased noise errors in the blue band [63,131,132], the atmospheric correction by combining UV and SWIR bands may provide a choice for extremely turbid waters.

5. Conclusions

In this study, we evaluated the Rrs product performance of multiple satellite ocean color sensors in the highly turbid waters of HZB in comparison to in situ data. Results showed that the Rrs products of GOCI and SGLI/GCOM-C contained limited effective Rrs data at the HTYZ site. COCTS/HY1C, OLCI/S3A, OLCI/S3B, and VIIRS/SNPP significantly underestimated Rrs at the HTYZ site and showed poor consistency with the in situ data, with PD values of –35.19%, –20.16%, –25.30%, and –34.87%, respectively, and APD values of 44.91%, 47.36%, 46.12%, and 44.48%, respectively. Among these four sensors, VIIRS/SNPP obtained the largest R value, while OLCI/S3A obtained the best PD value. The APD values of these four remote sensors are close, all around 45%. As a comparison, we also evaluated the performance of the Rrs products in moderately turbid waters at the ARIAKE site. Results showed that COCTS/HY1C (PD = –36.29%, APD = 51.34%) and SGLI/GCOM-C (PD = –34.65%, APD = 57.29%) significantly underestimated Rrs, while the performance of GOCI (PD = 12.98%, APD = 35.38%), OLCI/S3A (PD = –13.15%, APD = 27.87%), OLCI/S3B (PD = –3.66%, APD = 31.08%), and VIIRS/SNPP (PD = –11.64%, APD = 28.34%) was relatively good. Overall, our results revealed that the Rrs products from all six sensors do not provide reliable results in highly turbid waters. Therefore, atmospheric correction algorithms for highly turbid waters should be developed further.