Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting
Abstract
:1. Introduction
2. Methods
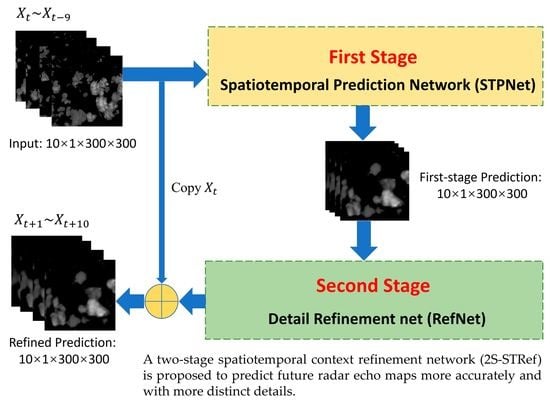
- A new two-stage precipitation prediction framework is proposed. On the basis of the spatiotemporal sequence prediction model capturing the spatiotemporal sequence, a two-stage model is designed to refine the output.
- An efficient and concise prediction model of the spatiotemporal sequence is constructed to learn spatiotemporal context information from past radar echo maps and output the predicted sequence of radar echo maps in the first stage.
- In the second stage, a new structure of the refinement network (RefNet) is proposed. The details of the output images can be improved by multi-scale feature extraction and fusion residual block. Instead of predicting the radar echo map directly, our RefNet outputs the residual sequence for the last frame, which further improves the whole model’s ability to predict the radar echo maps and enhances the details.
2.1. Formulation of Prediction Problem
2.2. Network Structure
2.2.1. First Stage: Spatiotemporal Prediction Net
2.2.2. Second Stage: Detail Refinement Net
2.3. Loss Function
2.4. Implementation
3. Experiments
3.1. Radar Echo Image Dataset
3.2. Evaluation
3.3. Results
4. Conclusions
- The input and output dimensions of the model are fixed, and it does not deal with length or dimension variant input sequences. If different input numbers or input dimensions of radar echo maps are input, the model must be redesigned and retrained.
- The lack of explainability of deep learning models should be improved.
- Developing new models to further improve the prediction accuracy as well as enhance the predicted details of the radar echo images, especially for heavy rainfall.
- Since the lifetime of radar echo is finite, the predictability of radar echoes gradually deteriorates over time. When the lead time exceeds the echo lifetime, it is hard to predict the future radar echo in the initial state only based on radar data. Other meteorological parameters, such as wind, should be introduced into the extrapolation model in the future to improve the prediction accuracy of radar echo change and further increase the lead time of radar extrapolation.
- More radar echo reflectivity images in summer and winter periods will be selected and used to train the proposed network separately to enhance the prediction accuracy, since the physics and evolution behind each type is not the same.
- We will also try to build an operational nowcasting system using the proposed algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gneiting, T.; Raftery, A.E. Weather forecasting with ensemble methods. Science 2005, 310, 248–249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, N. Machine learning tapped to improve climate forecasts. Nature 2017, 548, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Schmid, F.; Wang, Y.; Harou, A. Nowcasting guidelines—A summary. In WMO-No. 1198; World Meteorological Organization: Geneva, Switzerland, 2017; Chapter 5. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5617–5627. [Google Scholar]
- Bromberg, C.L.; Gazen, C.; Hickey, J.J.; Burge, J.; Barrington, L.; Agrawal, S. Machine learning for precipitation nowcasting from radar images. In Proceedings of the Machine Learning and the Physical Sciences Workshop at the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 1–4. [Google Scholar]
- Qiu, M.; Zhao, P.; Zhang, K.; Huang, J.; Shi, X.; Wang, X.; Chu, W. A short-term rainfall prediction model using multi-task convolutional neural networks. In Proceedings of the IEEE International Conference on Data Mining, New Orleans, LA, USA, 18–21 November 2017; pp. 395–404. [Google Scholar]
- Bouget, V.; Béréziat, D.; Brajard, J.; Charantonis, A.; Filoche, A. Fusion of rain radar images and wind forecasts in a deep learning model applied to rain nowcasting. Remote Sens. 2021, 13, 246. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Marchuk, G. Numerical Methods in Weather Prediction; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Tolstykh, M.A.; Frolov, A.V. Some current problems in numerical weather prediction. Izv. Atmos. Ocean. Phys. 2005, 41, 285–295. [Google Scholar]
- Juanzhen, S.; Ming, X.; James, W.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Pinto, J. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar]
- Crane, R.K. Automatic cell detection and tracking. IEEE Trans. Geosci. Electron. 1979, 17, 250–262. [Google Scholar] [CrossRef]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Bowler, N.E.; Pierce, C.E.; Seed, A. Development of a precipitation nowcasting algorithm based upon optical flow techniques. J. Hydrol. 2004, 288, 74–91. [Google Scholar] [CrossRef]
- Bellon, A.; Zawadzki, I.; Kilambi, A.; Lee, H.C.; Lee, Y.H.; Lee, G. McGill algorithm for precipitation nowcasting by lagrangian extrapolation (MAPLE) applied to the South Korean radar network. Asia-Pac. J. Atmos. Sci. 2010, 46, 369–381. [Google Scholar] [CrossRef]
- Woo, W.-C.; Wong, W.-K. Operational application of optical flow techniques to radar-based rainfall nowcasting. Atmosphere 2017, 8, 48. [Google Scholar] [CrossRef] [Green Version]
- Germann, U.; Zawadzki, I. Scale-dependence of the predictability of precipitation from continental radar images. Part I: Description of the methodology. Mon. Weather Rev. 2002, 130, 2859–2873. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale dependence of the predictability of precipitation from continental radar images. Part II: Probability forecasts. J. Appl. Meteorol. 2004, 43, 74–89. [Google Scholar] [CrossRef]
- Chung, K.S.; Yao, I.A. Improving radar echo Lagrangian extrapolation nowcasting by blending numerical model wind information: Statistical performance of 16 typhoon cases. Mon. Weather Rev. 2020, 148, 1099–1120. [Google Scholar] [CrossRef]
- Seed, A.W. A dynamic and spatial scaling approach to advection forecasting. J. Appl. Meteorol. 2003, 42, 381–388. [Google Scholar] [CrossRef]
- Ryu, S.; Lyu, G.; Do, Y.; Lee, G. Improved rainfall nowcasting using Burgers’ equation. J. Hydrol. 2020, 581, 124140. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Nerini, D.; Pérez Hortal, A.A.; Velasco-Forero, C.; Seed, A.; Germann, U.; Foresti, L. Pysteps: An open-source Python library for probabilistic precipitation nowcasting (v1. 0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Li, X.; Ye, Y.; Pengfei, X.; Yan, L. A generative adversarial gated recurrent unit model for precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2019, 17, 601–605. [Google Scholar] [CrossRef]
- Hernández, E.; Sanchez-Anguix, V.; Julian, V.; Palanca, J.; Duque, N. Rainfall prediction: A deep learning approach. In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Seville, Spain, 18–20 April 2016; pp. 151–162. [Google Scholar]
- Cyril, V.; Marc, M.; Christophe, P.; Marie-Laure, N. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar]
- McGovern, A.; Elmore, K.L.; Gagne, D.J.; Haupt, S.E.; Karstens, C.D.; Lagerquist, R.; Williams, J.K. Using artificial intelligence to improve real-time decision-making for high-impact weather. Bull. Am. Meteorol. Soc. 2017, 98, 2073–2090. [Google Scholar] [CrossRef]
- Wang, B.; Lu, J.; Yan, Z.; Luo, H.; Li, T.; Zheng, Y.; Zhang, G. Deep uncertainty quantification: A machine learning approach for weather forecasting. In Proceedings of the International Conference on Knowledge Discovery and data Mining (SIGKDD) 2019, Anchorage, AK, USA, 4–8 August 2019; pp. 2087–2095. [Google Scholar]
- Imam Cholissodin, S. Prediction of rainfall using improved deep learning with particle swarm optimization. Telkomnika 2020, 18, 2498–2504. [Google Scholar] [CrossRef]
- Lin, T.; Li, Q.; Geng, Y.A.; Jiang, L.; Xu, L.; Zheng, D.; Zhang, Y. Attention-based dual-source spatiotemporal neural network for lightning forecast. IEEE Access 2019, 7, 158296–158307. [Google Scholar] [CrossRef]
- Basha, C.Z.; Bhavana, N.; Bhavya, P.; Sowmya, V. Rainfall prediction using machine learning & deep learning techniques. In Proceedings of the International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; pp. 92–97. [Google Scholar]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Salman, A. Single layer & multi-layer long short-term memory (LSTM) model with intermediate variables for weather forecasting. Procedia Comput. Sci. 2018, 135, 89–98. [Google Scholar]
- Benjamin, K.; Lior, W.; Yehuda, A. A dynamic convolutional layer for short range weather prediction. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4840–4848. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Philip, S.Y. PredRNN++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the International Conference on Machine Learning (PMLR), Beijing, China, 14–16 November 2018; pp. 5123–5132. [Google Scholar]
- Geng, Y.; Li, Q.; Lin, T.; Jiang, L.; Xu, L.; Zheng, D.; Yao, W.; Lyu, W.; Zhang, Y. Lightnet: A dual spatiotemporal encoder network model for lightning prediction. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2439–2447. [Google Scholar]
- Zhang, F.; Wang, X.; Guan, J.; Wu, M.; Guo, L. RN-Net: A deep learning approach to 0–2 h rainfall nowcasting based on radar and automatic weather station data. Sensors 2021, 21, 1981. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Du, J.; Wang, J.; Jiang, C.; Ren, Y. Satellite image prediction relying on GAN and LSTM neural networks. In Proceedings of the IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Mohamed, S. Skillful Precipitation nowcasting using deep generative models of radar. arXiv 2021, arXiv:2104.00954. [Google Scholar]
- Li, Y.; Lang, J.; Ji, L.; Zhong, J.; Wang, Z.; Guo, Y.; He, S. Weather forecasting using ensemble of spatial-temporal attention network and multi-layer perceptron. Asia-Pac. J. Atmos. Sci. 2020, 2020, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.I.; Maity, R. Hybrid deep learning approach for multi-step-ahead daily rainfall prediction using GCM simulations. IEEE Access 2020, 8, 52774–52784. [Google Scholar] [CrossRef]
- Eddy, I.; Nikolaus, M.; Tonmoy, S.; Margret, K.; Alexey, D.; Thomas, B. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2462–2470. [Google Scholar]
- Liu, H.B.; Lee, I. MPL-GAN: Toward realistic meteorological predictive learning using conditional GAN. IEEE Access 2020, 8, 93179–93186. [Google Scholar] [CrossRef]
- Schultz, M.G.; Betancourt, C.; Gong, B.; Kleinert, F.; Langguth, M.; Leufen, L.H.; Stadtler, S. Can deep learning beat numerical weather prediction? Philos. Trans. R. Soc. A 2021, 379, 20200097. [Google Scholar] [CrossRef] [PubMed]
- Seed, A.W.; Pierce, C.E.; Norman, K. Formulation and evaluation of a scale decomposition-based stochastic precipitation nowcast scheme. Water Resour. Res. 2013, 49, 6624–6641. [Google Scholar] [CrossRef]
- Qin, J.; Huang, Y.; Wen, W. Multi-scale feature fusion residual network for single image super-resolution. Neurocomputing 2020, 379, 334–342. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, J.; Yang, Y. Deep fractal residual network for fast and accurate single image super resolution. Neurocomputing 2020, 398, 389–398. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Diederik, K.; Jimmy, B. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Hansoo, L.; Sungshin, K. Ensemble classification for anomalous propagation echo detection with clustering-based subset-selection method. Atmosphere 2017, 8, 11. [Google Scholar]
- Song, K.; Yang, G.; Wang, Q.; Xu, C.; Liu, J.; Liu, W.; Zhang, W. Deep learning prediction of incoming rainfalls: An operational service for the city of Beijing, China. In Proceedings of the 2019 International Conference on Data Mining Workshops (ICDMW), Beijing, China, 8–11 November 2019; pp. 180–185. [Google Scholar]












| Name | Kernel | Stride | L | Channels Input/Output |
|---|---|---|---|---|
| Conv1 | 5 × 5 | 3 × 3 | − | 1/8 |
| ST-RNN1 | 3 × 3 | 1 × 1 | 13 | 8/64 |
| Conv2 | 3 × 3 | 2 × 2 | − | 64/64 |
| ST-RNN2 | 3 × 3 | 1 × 1 | 13 | 64/192 |
| Conv3 | 3 × 3 | 2 × 2 | − | 192/192 |
| ST-RNN3 | 3 × 3 | 1 × 1 | 9 | 192/192 |
| Name | Kernel | Stride | L | Channels Input/Output |
|---|---|---|---|---|
| ST-RNN1 | 3 × 3 | 1 × 1 | 9 | 192/192 |
| DeConv1 | 4 × 4 | 2 × 2 | − | 192/192 |
| ST-RNN2 | 3 × 3 | 1 × 1 | 13 | 192/192 |
| DeConv2 | 4 × 4 | 2 × 2 | − | 192/192 |
| ST-RNN3 | 3 × 3 | 1 × 1 | 13 | 192/64 |
| DeConv3 | 5 × 5 | 3 × 3 | − | 64/8 |
| Hyper-Parameter | Value |
|---|---|
| numbers of hidden states | 64, 128, 256 |
| kernel sizes | 3 × 3 |
| Rotation angle | 30° |
| Optimizer | Adam (β1 = 0.9, β2 = 0.999) |
| Minibatch size | 4 |
| Learning rate | 1 × 10−4 |
| Framework | Pytorch 1.7 |
| GPU | NVIDIA RTX 3090 |
| Year | Images | Daily Event |
|---|---|---|
| 2017 | 17,400 | 145 |
| 2018 | 13,080 | 109 |
| 2019 | 12,240 | 102 |
| MODEL | SSIM (One-Hour Prediction) ↑ | SSIM (Two-Hour Prediction) ↑ |
|---|---|---|
| OpticalFlow [17] (ROVER) | 0.616 | 0.577 |
| Pysteps [23] (Extrapolation) | 0.626 | 0.589 |
| Pysteps [23] (S-PROG) | 0.678 | 0.645 |
| ConvLSTM [9] | 0.634 | 0.579 |
| PredRNN++ [37] | 0.676 | 0.648 |
| STPNet | 0.675 | 0.654 |
| 2S-STRef | 0.694 | 0.665 |
| MODEL | CSI ↑ | HSS ↑ | POD ↑ | FAR ↓ |
|---|---|---|---|---|
| OpticalFlow [17] (ROVER) | 0.490 | 0.563 | 0.627 | 0.322 |
| Pysteps [23] (Extrapolation) | 0.480 | 0.554 | 0.600 | 0.312 |
| Pysteps [23] (S-PROG) | 0.501 | 0.578 | 0.620 | 0.293 |
| ConvLSTM [9] | 0.552 | 0.645 | 0.725 | 0.289 |
| PredRNN++ [37] | 0.576 | 0.653 | 0.731 | 0.277 |
| STPNet | 0.584 | 0.663 | 0.728 | 0.259 |
| 2S-STRef | 0.588 | 0.665 | 0.747 | 0.272 |
| MODEL | CSI ↑ | HSS ↑ | POD ↑ | FAR ↓ |
|---|---|---|---|---|
| OpticalFlow [17] (ROVER) | 0.317 | 0.441 | 0.455 | 0.519 |
| Pysteps [23] (Extrapolation) | 0.315 | 0.438 | 0.442 | 0.512 |
| Pysteps [23] (S-PROG) | 0.326 | 0.452 | 0.458 | 0.502 |
| ConvLSTM [9] | 0.352 | 0.508 | 0.602 | 0.510 |
| PredRNN++ [37] | 0.378 | 0.513 | 0.611 | 0.516 |
| STPNet | 0.393 | 0.530 | 0.626 | 0.500 |
| 2S-STRef | 0.398 | 0.536 | 0.611 | 0.480 |
| MODEL | CSI ↑ | HSS ↑ | POD ↑ | FAR ↓ |
|---|---|---|---|---|
| OpticalFlow [17] (ROVER) | 0.129 | 0.212 | 0.207 | 0.772 |
| Pysteps [23] (Extrapolation) | 0.133 | 0.214 | 0.209 | 0.768 |
| Pysteps [23] (S-PROG) | 0.127 | 0.198 | 0.197 | 0.789 |
| ConvLSTM [9] | 0.166 | 0.277 | 0.319 | 0.743 |
| PredRNN++ [37] | 0.184 | 0.296 | 0.362 | 0.740 |
| STPNet | 0.192 | 0.308 | 0.373 | 0.728 |
| 2S-STRef | 0.195 | 0.312 | 0.373 | 0.721 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, D.; Huang, J.; Zang, Z.; Xu, L.; Che, H.; Tang, Y. Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting. Remote Sens. 2021, 13, 4285. https://doi.org/10.3390/rs13214285
Niu D, Huang J, Zang Z, Xu L, Che H, Tang Y. Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting. Remote Sensing. 2021; 13(21):4285. https://doi.org/10.3390/rs13214285
Chicago/Turabian StyleNiu, Dan, Junhao Huang, Zengliang Zang, Liujia Xu, Hongshu Che, and Yuanqing Tang. 2021. "Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting" Remote Sensing 13, no. 21: 4285. https://doi.org/10.3390/rs13214285
APA StyleNiu, D., Huang, J., Zang, Z., Xu, L., Che, H., & Tang, Y. (2021). Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting. Remote Sensing, 13(21), 4285. https://doi.org/10.3390/rs13214285