A Meta-Learning Approach of Optimisation for Spatial Prediction of Landslides
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Study Area
2.2. Geospatial Database
2.2.1. Landslide Inventory
2.2.2. Landslide Causative Factors
2.3. Methodology
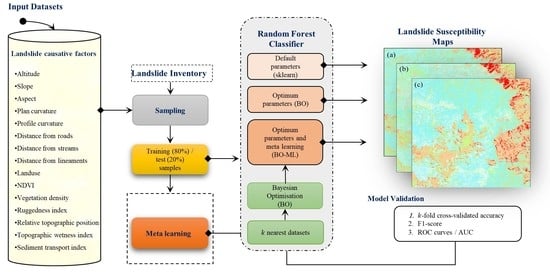
2.3.1. Overall Esearch Methodology
2.3.2. Modelling: Random Forest
- RF is ideal for working with mixed variables, i.e., both categorical and numerical, most likely in landslide modelling,
- In RF, each tree has access to specific subspace feature sets. This random selection of features to split each node contributes to a favourable error rate. This randomness also offers high accuracy rates for outliers in predictors, and
- RF is a good feature engineering tool. That means finding the most relevant features from the training dataset.
2.3.3. Optimisation: Bayesian Optimisation
2.3.4. Proposed Meta-Learning Optimisation Approach
2.3.5. Performance Assessment
2.3.6. The Relative Importance of Causative Factors
3. Results
3.1. Performance of RF with Default Values of Hyperparameters
3.2. Performance of RF with Optimised Values of Hyperparameters
3.3. Landslide Susceptibility Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LiDAR | light detection and ranging |
| RADAR | radio detection and ranging |
| CNN | convolutional neural networks |
| RNN | recurrent neural networks |
| BO | bayesian optimization |
| BO-ML | bayesian optimization via meta-learning |
| ANN | artificial neural network |
| SVM | support vector machine |
| RF | random forest |
| MFO | moth flame optimiser |
| DEM | digital elevation model |
| MCC | multiscale curvature classification |
| IDW | inverse distance weighted |
| NDVI | normalised difference vegetation index |
| RI | ruggedness index |
| RMSD | root-mean-square-deviation |
| RTP | relative topographic position |
| TWI | topographic wetness index |
| STI | sediment transport index |
| AOI | area of interest |
| AUROC | receiving operating characteristic curves |
| OOB | out-of-bag |
| GP | gaussian process |
Appendix A



Appendix B
| Parameter | Explanation | Necessity of Tuning |
|---|---|---|
| Number of estimators or trees | Number of trees to create the RF. | At higher numbers of trees, the RF is relatively stable, but at one point it can still overfit and time complexity of the model can increase. This should be tuned. |
| Criterion | Function to measure split quality. Gini impurity and information gain are two common functions. | Both Gini and information gain impurity metrics work well. However, the latter is more computationally heavy due to the log in the Entropy equation. |
| Maximum depth | Tree’s maximum depth. The longest path between root and leaf node or max number of splits possible within each tree | Since this parameter is used to control over-fitting as higher depth allows the model to learn very detailed relationships to a particular sample, it should be tuned. |
| Maximum features | Number of features to consider when looking for best splitting. These are randomly selected. | The square root of the total number of features is suggested as a thumb-rule. The lower is greater for the reduction of variance, however, the bias will increase. Higher values can lead to over-fitting. It should, therefore, be tuned. |
| Minimum samples leaf | Defines the minimum samples required in a terminal node or leaf. | This can smooth the model. A smaller leaf makes the model more prone to capturing noise in train data and should, therefore, be tuned. |
| Minimum samples split | Specifies the minimum number of samples required for splitting in a node. | To control over-fitting. Higher values prevent a model from learning relationships that could be very specific to the particular sample selected for a tree. Too high values can also contribute to underfitting. |
Appendix C
| Meta Features | Equation | Explanation | Rationale |
|---|---|---|---|
| Basic features (simple features related to dataset attributes) | |||
| Nr instances | The number of samples in the dataset. | Speed, Scalability | |
| Log Nr instances | Natural log of the number of samples. | ||
| Nr features | The number of causative factors in the dataset. | Curse of dimensionality | |
| Log Nr features | Natural log of the number of causative factors. | ||
| Nr numeric features | The number of causative factors that are numeric. | Complexity, imbalance | |
| Nr categorical features | The number of causative factors that are categorical. | ||
| Ratio numerical/nominal | The ratio between numerical to categorical factors. | Complexity, imbalance | |
| Ratio nominal/numerical | The ratio between the categorical to numerical factors. | ||
| Dataset ratio | The ratio between the numbers of factors to the number of samples. | Curse of dimensionality | |
| Log dataset ratio | Natural log of the dataset ratio (Number of causative factors divided by number of samples). | ||
| Inverse dataset ratio | The ratio between the numbers of samples to the number of factors. | ||
| Log inverse dataset ratio | Natural log of the inverse dataset ratio (Number of samples divided by number of causative factors). | ||
| Num. symbols | The number of unique labels in categorical factors. | Complexity, imbalance | |
| Statistical features (features describe statistical properties of the dataset) | |||
| Kurtosis | List of kurtosis values for the causative factors. It identifies as whether the tails of data distribution of a given values contain extreme values. The distributions with large kurtosis values are ones where there is the possibility of extreme values, and vice versa. | Feature normality | |
| Kurtosis (min) | Minimum kurtosis. | ||
| Kurtosis (max) | Maximum kurtosis. | ||
| Kurtosis (mean) | Mean kurtosis. | ||
| Kurtosis (std.) | Standard deviation kurtosis. | ||
| Skewness | List of skewness values for the causative factors. It defines the measure of the symmetry of data distribution for a given value. When is far below its mean is a big negative number, and when is far above its mean is a big positive number. | Feature normality | |
| Skewness (min) | Minimum skewness. | ||
| Skewness (max) | Maximum skewness. | ||
| Skewness (mean) | Mean skewness. | ||
| Skewness (std.) | Standard deviation skewness. | ||
| Minimums | Minimum values of the causative factors. | Locality, Data distribution | |
| Maximums | Maximum values of the causative factors. | ||
| Means | Mean values of the causative factors. | ||
| Stds | Standard deviation values of the causative factors. | ||
References
- Zhu, Q.; Chen, L.; Hu, H.; Xu, B.; Zhang, Y.; Li, H. Deep Fusion of Local and Non-Local Features for Precision Landslide Recognition. arXiv 2020, arXiv:2002.08547. [Google Scholar]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Xie, W.; Nie, W.; Saffari, P.; Robledo, L.F.; Descote, P.Y.; Jian, W. Landslide hazard assessment based on Bayesian optimization–support vector machine in Nanping City, China. Nat. Hazards 2021, 109, 931–948. [Google Scholar] [CrossRef]
- Zhou, C.; Lee, C.; Li, J.; Xu, Z. On the spatial relationship between landslides and causative factors on Lantau Island, Hong Kong. Geomorphology 2002, 43, 197–207. [Google Scholar] [CrossRef]
- Weng, M.-C.; Wu, M.-H.; Ning, S.-K.; Jou, Y.-W. Evaluating triggering and causative factors of landslides in Lawnon River Basin, Taiwan. Eng. Geol. 2011, 123, 72–82. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (LiDAR) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Chang, K.-T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating scale effects of topographic variables in landslide susceptibility models using GIS-based machine learning techniques. Sci. Rep. 2019, 9, 12296. [Google Scholar] [CrossRef] [Green Version]
- Kanungo, D.; Arora, M.; Sarkar, S.; Gupta, R. A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas. Eng. Geol. 2006, 85, 347–366. [Google Scholar] [CrossRef]
- Luo, X.; Lin, F.; Zhu, S.; Yu, M.; Zhang, Z.; Meng, L.; Peng, J. Mine landslide susceptibility assessment using IVM, ANN and SVM models considering the contribution of affecting factors. PLoS ONE 2019, 14, e0215134. [Google Scholar] [CrossRef]
- Conoscenti, C.; Rotigliano, E.; Cama, M.; Caraballo-Arias, N.A.; Lombardo, L.; Agnesi, V. Exploring the effect of absence selection on landslide susceptibility models: A case study in Sicily, Italy. Geomorphology 2016, 261, 222–235. [Google Scholar] [CrossRef]
- Erener, A.; Sivas, A.A.; Selcuk-Kestel, A.S.; Düzgün, H.S. Analysis of training sample selection strategies for regression-based quantitative landslide susceptibility mapping methods. Comput. Geosci. 2017, 104, 62–74. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.; Pradhan, B.; Kalantar, B.; Sameen, M.I.; Santosh, M.; Alamri, A. Landslide susceptibility modeling: An integrated novel method based on machine learning feature transformation. Remote Sens. 2021, 13, 3281. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Saleem, N.; Huq, M.; Twumasi, N.Y.; Javed, A.; Sajjad, A. Parameters derived from and/or used with digital elevation models (DEMs) for landslide susceptibility mapping and landslide risk assessment: A review. ISPRS Int. J. Geo-Inf. 2019, 8, 545. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Lu, Z. Remote sensing of landslides—A review. Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef] [Green Version]
- Gaidzik, K.; Ramírez-Herrera, M.T. The importance of input data on landslide susceptibility mapping. Sci. Rep. 2021, 11, 19334. [Google Scholar] [CrossRef]
- Al-Najjar, H.H.; Pradhan, B. Spatial landslide susceptibility assessment using machine learning techniques assisted by additional data created with generative adversarial networks. Geosci. Front. 2021, 12, 625–637. [Google Scholar] [CrossRef]
- Tanyu, B.F.; Abbaspour, A.; Alimohammadlou, Y.; Tecuci, G. Landslide susceptibility analyses using Random Forest, C4.5, and C5. 0 with balanced and unbalanced datasets. Catena 2021, 203, 105355. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Pradhan Sarkar, R.; Beydoun, G.; Alamri, A. A New Integrated Approach for Landslide Data Balancing and Spatial Prediction Based on Generative Adversarial Networks (GAN). Remote Sens. 2021, 13, 4011. [Google Scholar] [CrossRef]
- Huang, B.; Zheng, W.; Yu, Z.; Liu, G. A successful case of emergency landslide response-the Sept. 2, 2014, Shanshucao landslide, Three Gorges Reservoir, China. Geoenviron. Disasters 2015, 2, 18. [Google Scholar] [CrossRef] [Green Version]
- Sahin, E.K.; Colkesen, I.; Acmali, S.S.; Akgun, A.; Aydinoglu, A.C. Developing comprehensive geocomputation tools for landslide susceptibility mapping: LSM tool pack. Comput. Geosci. 2020, 144, 104592. [Google Scholar] [CrossRef]
- Nguyen, T.T.N.; Liu, C.-C. A new approach using AHP to generate landslide susceptibility maps in the Chen-Yu-Lan Watershed, Taiwan. Sensors 2019, 19, 505. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Kadavi, P.R.; Lee, C.-W.; Lee, S. Application of ensemble-based machine learning models to landslide susceptibility mapping. Remote Sens. 2018, 10, 1252. [Google Scholar] [CrossRef] [Green Version]
- Melchiorre, C.; Abella, E.C.; van Westen, C.J.; Matteucci, M. Evaluation of prediction capability, robustness, and sensitivity in non-linear landslide susceptibility models, Guantánamo, Cuba. Comput. Geosci. 2011, 37, 410–425. [Google Scholar] [CrossRef]
- Gao, H.; Fam, P.S.; Tay, L.; Low, H. An overview and comparison on recent landslide susceptibility mapping methods. Disaster Adv. 2019, 12, 46–64. [Google Scholar]
- Kotthoff, L.; Thornton, C.; Hoos, H.H.; Hutter, F.; Leyton-Brown, K. Auto-WEKA: Automatic model selection and hyperparameter optimization in WEKA. In Automated Machine Learning; Springer: Cham, Germany, 2019; pp. 81–95. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 282–305. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 1–9. [Google Scholar]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z. A comparative study of landslide susceptibility mapping using SVM and PSO-SVM models based on Grid and Slope Units. Math. Probl. Eng. 2021, 2021, 8854606. [Google Scholar]
- Liu, Y.; Zhang, Y.X. Application of optimized parameters SVM in deformation prediction of creep landslide tunnel. In Proceedings of the Applied Mechanics and Materials; Trans Tech Publications: Freinbach, Switzerland, 2014; pp. 265–268. [Google Scholar]
- Micheletti, N.; Foresti, L.; Robert, S.; Leuenberger, M.; Pedrazzini, A.; Jaboyedoff, M.; Kanevski, M. Machine learning feature selection methods for landslide susceptibility mapping. Math. Geosci. 2014, 46, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Karell, L.; Muňko, M.; Ďuračiová, R. Applicability of Support Vector Machines in Landslide Susceptibility Mapping. In The Rise of Big Spatial Data; Springer: Berlin/Heidelberg, Germany, 2017; pp. 373–386. [Google Scholar]
- Nam, K.; Wang, F. An extreme rainfall-induced landslide susceptibility assessment using autoencoder combined with random forest in Shimane Prefecture, Japan. Geoenviron. Disasters 2020, 7, 6. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Pham, V.D.; Nguyen, Q.-H.; Nguyen, H.-D.; Pham, V.-M.; Bui, Q.-T. Convolutional neural network—Optimized moth flame algorithm for shallow landslide susceptible analysis. IEEE Access 2020, 8, 32727–32736. [Google Scholar] [CrossRef]
- Feurer, M.; Springenberg, J.; Hutter, F. Initializing bayesian hyperparameter optimization via meta-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Mantovani, R. Use of Meta-Learning for Hyperparameter Tuning of Classification Problems. Ph.D. Thesis, University of Sao Carlos, Sao Carlos, Brazil, 2018. [Google Scholar]
- Vanschoren, J. Meta-learning: A survey. arXiv 2018, arXiv:1810.03548. [Google Scholar]
- Nhu, V.H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Geertsema, M.; Kress, V.R.; Karimzadeh, S.; Valizadeh Kamran, K.; et al. Landslide detection and susceptibility modeling on cameron highlands (Malaysia): A comparison between random forest, logistic regression and logistic model tree algorithms. Forests 2020, 11, 830. [Google Scholar] [CrossRef]
- Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return LiDAR in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Mezaal, M.R.; Pradhan, B.; Sameen, M.I.; Mohd Shafri, H.Z.; Yusoff, Z.M. Optimized neural architecture for automatic landslide detection from high-resolution airborne laser scanning data. Appl. Sci. 2017, 7, 730. [Google Scholar] [CrossRef] [Green Version]
- Garrido-Merchán, E.C.; Hernández-Lobato, D. Dealing with categorical and integer-valued variables in bayesian optimization with gaussian processes. Neurocomputing 2020, 380, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Rosin, P.L.; Martin, R.; Langbein, F. Fast and effective feature-preserving mesh denoising. IEEE Trans. Vis. Comput. Graph. 2007, 13, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Walker, L.R.; Shiels, A.B. Landslide Ecology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Puente, M.; Bashan, Y.; Li, C.; Lebsky, V. Microbial populations and activities in the rhizoplane of rock-weathering desert plants. I. Root colonization and weathering of igneous rocks. Plant Biol. 2004, 6, 629–642. [Google Scholar] [CrossRef] [Green Version]
- Sadr, M.P.; Hassani, H.; Maghsoudi, A. Slope Instability Assessment using a weighted overlay mapping method, A case study of Khorramabad-Doroud railway track, W Iran. J. Tethys 2014, 2, 254–271. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Digital terrain analysis. Terrain Anal. Princ. Appl. 2000, 6, 1–27. [Google Scholar]
- Mandal, S.; Maiti, R. Semi-Quantitative Approaches for Landslide Assessment and Prediction; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall Induced Landslide Susceptibility Mapping Based on Bayesian Optimized Random Forest and Gradient Boosting Decision Tree Models—A Case Study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
- Ercanoglu, M. Landslide susceptibility assessment of SE Bartin (West Black Sea region, Turkey) by artificial neural networks. Nat. Hazards Earth Syst. Sci. 2005, 5, 979–992. [Google Scholar] [CrossRef] [Green Version]
- Glade, T. Vulnerability assessment in landslide risk analysis. Erde 2003, 134, 123–146. [Google Scholar]
- Lallianthanga, R.; Lalbiakmawia, F.; Lalramchuana, F. Landslide hazard zonation of Mamit Town, Mizoram, India using remote sensing and GIS techniques. Int. J. Geol. Earth Environ. Sci. 2013, 3, 184–194. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Bernard, S.; Heutte, L.; Adam, S. On the selection of decision trees in random forests. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 302–307. [Google Scholar]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michie, D.; Spiegelhalter, D.J.; Taylor, C.C. Machine learning, neural and statistical classification. Technometrics 1994, 37, 459. [Google Scholar]
- Toloşi, L.; Lengauer, T. Classification with correlated features: Unreliability of feature ranking and solutions. Bioinformatics 2011, 27, 1986–1994. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Performance evaluation and hyperparameter tuning of statistical and machine-learning models using spatial data. arXiv 2018, arXiv:1803.11266. [Google Scholar]
- Kalousis, A. Algorithm Selection via Meta-Learning. Ph.D. Thesis, University of Geneva, Geneva, Switzerland, 2002. [Google Scholar]
- Henery, R. Methods for comparison. In Machine Learning, Neural and Statistical Classification; Michie, D., Spiegelhalter, D., Taylor, C., Eds.; Ellis Horwood: Hemel, UK, 1994; pp. 107–124. [Google Scholar]
- Alcobaça, E.; Siqueira, F.; Rivolli, A.; Garcia, L.P.; Oliva, J.T.; de Carvalho, A.C. MFE: Towards reproducible meta-feature extraction. J. Mach. Learn. Res. 2020, 21, 1–5. [Google Scholar]
- Filchenkov, A.; Pendryak, A. Datasets meta-feature description for recommending feature selection algorithm. In Proceedings of the 2015 Artificial Intelligence and Natural Language and Information Extraction, Social Media and Web Search FRUCT Conference (AINL-ISMW FRUCT), St. Petersburg, Russia, 9–14 November 2015; pp. 11–18. [Google Scholar]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Dang, V.-H.; Hoang, N.-D.; Nguyen, L.-M.-D.; Bui, D.T.; Samui, P. A novel GIS-based random forest machine algorithm for the spatial prediction of shallow landslide susceptibility. Forests 2020, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Gilbert, G.; Cepeda, J.M.; Lysdahl, A.O.; Piciullo, L.; Hefre, H.; Lacasse, S. Modelling of shallow landslides with machine learning algorithms. Eng. Geol. 2021, 12, 385–393. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Dou, J.; Oguchi, T.; Hayakawa, Y.S.; Uchiyama, S.; Saito, H.; Paudel, U. GIS-based landslide susceptibility mapping using a certainty factor model and its validation in the Chuetsu Area, Central Japan. In Landslide Science for a Safer Geoenvironment; Springer: Berlin/Heidelberg, Germany, 2014; pp. 419–424. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Selecting optimal conditioning factors in shallow translational landslide susceptibility mapping using genetic algorithm. Eng. Geol. 2015, 192, 101–112. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I.; Sahin, E.K. Machine learning techniques in landslide susceptibility mapping: A survey and a case study. Landslides Theory Pract. Model. 2019, 50, 283–301. [Google Scholar]
- Torra, V.; Narukawa, Y. Modeling Decisions for Artificial Intelligence: Second International Conference, MDAI 2005, Tsukuba, Japan, 25–27 July 2005; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Barthold, F.; Blank, B.; Kögel-Knabner, I. Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem. Plant Soil 2011, 340, 7–24. [Google Scholar] [CrossRef]
- Kuhnert, P.M.; Martin, T.G.; Griffiths, S.P. A guide to eliciting and using expert knowledge in Bayesian ecological models. Ecol. Lett. 2010, 13, 900–914. [Google Scholar] [CrossRef] [PubMed]
- McKay, G.; Harris, J.R. Comparison of the data-driven random forests model and a knowledge-driven method for mineral prospectivity mapping: A case study for gold deposits around the Huritz Group and Nueltin Suite, Nunavut, Canada. Nat. Resour. Res. 2016, 25, 125–143. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Sun, D.; Xu, J.; Wen, H.; Wang, D. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization: A comparison between logistic regression and random forest. Eng. Geol. 2021, 281, 105972. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Behnia, P.; Blais-Stevens, A. Landslide susceptibility modelling using the quantitative random forest method along the northern portion of the Yukon Alaska Highway Corridor, Canada. Nat. Hazards 2018, 90, 1407–1426. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]








| Data | Data Source(s) | Type | Scale or Spatial Resolution |
|---|---|---|---|
| LiDAR data | The data were acquired with an airborne-based system on 15 January 2015. The system had a 25,000 Hz pulse frequency rate | Point clouds | 8 points/m2 (point density). The absolute vertical and horizontal precisions were 0.15 m and 0.3 m, respectively. |
| High-resolution orthophotos | The data was acquired using the same LiDAR system and at the same time. | Grid | 10 cm ground sampling distance at 1/1000 scale. |
| A digital elevation model (DEM) | The data was created from the LiDAR point clouds using only ground points. | Grid | 2 m |
| Satellite images | Landsat 7/ETM+ | Grid | 30 m |
| Administrative division/subdivisions | https://gadm.org/ (access on 8 October 2020) | Vector | |
| Land use | Aerial photos + LiDAR data | Vector | |
| Geological data | Vector | ||
| River network | Extracted based on DEM | Vector | |
| Road network | Vector | ||
| Historical landslides | Prepared based on an existing inventory map [46]. | Vector/Datasheet |
| Factor | ||||
|---|---|---|---|---|
| Altitude (m) | 1443 | 1909 | 1603.48 | 74.67 |
| Slope (°) | 4.7 | 42 | 30.79 | 8.30 |
| Aspect (°) | 34 | 286 | 165.60 | 63.81 |
| Plan curvature | 4.300e+02 | 4.102e+13 | 3.061e+12 | 8.770e+12 |
| Profile curvature | −19,634 | 122,469 | 4121.13 | 18,128.16 |
| Distance from roads (m) | 6.2 | 233 | 43.74 | 41.57 |
| Distance from streams (m) | 3.8 | 114 | 49.80 | 27.40 |
| Distance from lineaments (m) | 9.6 | 203.5 | 85.55 | 45.92 |
| Land use | Categorical variable | |||
| Normalised difference vegetation index | 0.099 | 0.52 | 0.377 | 0.081 |
| Vegetation density | Categorical variable | |||
| Ruggedness index | 0.61 | 73 | 3.92 | 9.55 |
| Relative topographic position | −0.007 | 0.48 | 0.15 | 0.12 |
| Topographic wetness index | 0.64 | 3.6 | 1.37 | 0.61 |
| Sediment transport index | 0.68 | 57 | 10.18 | 7.23 |
| Factor | Equation/Calculation Method | Rationale |
|---|---|---|
| Altitude (m) | Extracted from the smoothed version of DEM (calculated by the de-noising algorithm described by [48]. | Elevated area affects slope loading. Higher altitude areas increase the likelihood of landslides, especially if the orientation of the sliding plane is closer to open excavation [49], Altitude also affects the extent of rock weathering [50]. |
| Slope (°) | A significant topographic parameter in any landslide susceptibility study and commonly used in previous research [3,44]. Higher landslide frequency is often found in steep slopes [33,44]. | |
| Aspect (°) | Regulates topographic moisture levels influenced by solar radiation and precipitation [51]. | |
| Plan curvature | Calculated using the equation for the calculation of plan curvature as [52]. Plan curvature is negative for diverging flow along ridges and positive for convergent areas, e.g., along valley bottoms. | Curvature represents slope changes along a curve’s tiny arcs, influencing slope instability by altering landform character [53]. Plan curvature is the curvature perpendicular to the direction of the peak slope. The convex surface drains moisture immediately while the concave surface holds moisture for long. |
| Profile curvature | Calculated using the same equation for the calculation of plan curvature as [52]. Profile curvature is negative for slope increasing downhill (convex flow profile, typical of upper slopes) and positive for slope decreasing downhill (concave, typical of lower slopes). | Profile curvature refers to the convergence and flow divergence across a surface. |
| Distance from roads (m) | For each cell, the Euclidean distance to the closest road feature was calculated. | A landslide susceptibility assessment routinely uses anthropogenic factors such as distance from roads. Some of the most common actions during construction are shallow to deep excavations, foreign load application, and vegetative cover removal along highways and roads [54]. |
| Distance from streams (m) | For each cell, the Euclidean distance to the closest stream feature was calculated. | A hydrological community’s intermittent flow regime and gullies encompass erosive and saturation processes. Subsequently, pore water pressure may increase, leading to landslides in areas adjacent to drainage channels [54]. |
| Distance from lineaments (m) | For each cell, the Euclidean distance to the closest lineament feature was calculated. | Lithological factors are used in many landslide research; these affect the type and mechanism of landslides as rocks differ in terms of internal structure, mineral composition, and susceptibility to landslides [55]. |
| Land use | Prepared from 10m SPOT 5 satellite images using maximum likelihood classification. 10 land use and land cover types were identified, e.g., water, transportation, agriculture, residential and bare land. The classified map’s overall accuracy was 87.20%, verified with field surveys. | Human activities influence patterns of land use, contributing to landslides [56], more common in barren areas than forests and residential areas [57]. |
| Normalised difference vegetation index (NDVI) | NDVI is highly correlated with photosynthesis activity, hence with vegetation density [58] Greater NDVI values mean more amount of vegetation cover. | |
| Vegetation density | The area was divided into four classes of vegetation densities, i.e., non-vegetation, low-density, moderate-density, and high-density vegetation. Non-vegetated areas were identified based on aggregating non-vegetation classes of land use data. The three density levels of vegetation were determined by classifying the NDVI raster using (0.176–0.286, 0.287–0.417, 0.418–1.0) ranges for the three classes, respectively. | Vegetation cover plays an important role in causing landslides in Cameron Highlands. Such areas are vulnerable to unstable erosion. The vegetation root leads to hill slope stabilization and reduction in landslide occurrences. The higher vegetation density value indicates the higher vegetation concentration per area unit. |
| Ruggedness index (RI) | For each grid cell in the DEM, the root-mean-square-deviation (RMSD) is calculated using the residuals (i.e., elevation differences) between a grid cell and its eight neighbours. Details can be found in [59]. | Used to describe and quantify local relief. It also affects erosion and deposition rate, activity rates, and age of deposits. Changes in gradient result in increased rainfall accumulation and infiltration. |
| Relative topographic position (RTP) | An effective factor for landslides describes the expression of the geomorphological settings (slope, ridge, valley, etc.) in a quantitative way. It is included in landslide susceptibility studies because landslide events usually take place on the ridges. | |
| Topographic wetness index (TWI) | A steady-state wetness index representing flow accumulations down the slope impacting runoff velocity, hydrologic conditions. | |
| Sediment transport index (STI) | Related to the delivery of sediments from terrain into the channel during landslide events. The amount of sediment in a catchment indicates the potential sediment supply to the debris at the catchment mouth. |
| Hyperparameter | Value Type | Search Space |
|---|---|---|
| Number of estimators | Integer | [5, 500] |
| Criterion | Categorical | [“gini”, “entropy”] |
| Maximum depth | Integer | [1, 15] |
| Maximum features | Integer | [1, 15] |
| Minimum samples leaf | Integer | [5, 30] |
| Minimum samples split | Integer | [2, 100] |
| Dataset # | Shape ( ) | List of Chosen Factors |
|---|---|---|
| 1 | (70, 9) | [Vegetation density, Aspect, RI, Altitude, Slope, Distance from road, Distance from streams, LULC, distance from lineament] |
| 2 | (100, 15) | [Altitude, WI, NDVI, RTP, Distance from road, Distance from streams, Aspect, Distance from lineament, STI, Slope, LULC, Plan curvature, RI, Vegetation density] |
| 3 | (50, 8) | [Distance from lineament, Slope, Vegetation density, NDVI, RI, Profile curvature, Altitude, Aspect] |
| 4 | (120, 15) | [RTP, Aspect, Plan curvature, Distance from streams, Distance from roads, Vegetation density, Distance from lineament, LULC, NDVI, Profile curvature, Slope, Altitude, STI, RI, WI] |
| 5 | (70, 7) | [Plan curvature, RTP, Profile curvature, Aspect, WI, Distance from roads, Altitude] |
| 6 | (50, 13) | [STI, WI, RI, Distance from roads, Altitude, LULC, Profile curvature, Vegetation density, Distance from lineament, Slope, NDVI, RTP, Distance from streams] |
| 7 | (50, 7) | [LULC, Distance from streams, NDVI, Slope, Altitude, Aspect, WI] |
| 8 | (90, 14) | [RTP, Distance from roads, NDVI, Distance from lineament, Altitude, Aspect, STI, WI, RI, LULC, Vegetation density, Slope, Plan curvature, Distance from stream] |
| 9 | (80, 4) | [Distance from lineament, Distance from road, RTP, WI] |
| 10 | (50, 8) | [Slope, Distance from lineament, Altitude, Plan curvature, RI, WI, NDVI, RTP] |
| Parameter | Value | Explanation |
|---|---|---|
| Number of estimators | 100 | The number of trees in the forest. |
| Criterion | Gini | The function to measure the quality of a split. |
| Maximum depth | None | The maximum depth of the tree. |
| Maximum features | Auto | The number of features to consider when looking for the best split. |
| Minimum samples leaf | 1 | The minimum number of samples required to be at a leaf node. |
| Minimum samples split | 2 | The minimum number of samples required to split an internal node. |
| Dataset | Five-Fold Cv Accuracy | F1-Score | AUROC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Default | BO | BO-ML | Default | BO | BO-ML | Default | BO | BO-ML | |
| Training (80%) | 0.751 | 0.810 | 0.769 | 0.745 | 0.850 | 0.826 | 0.779 | 0.861 | 0.823 |
| Test (20%) | 0.732 | 0.802 | 0.800 | 0.727 | 0.852 | 0.832 | 0.761 | 0.864 | 0.820 |
| Dataset # | Number of Estimators | Criterion | Max. Depth | Max. Features | Min. Samples Leaf | Min. Samples Split |
|---|---|---|---|---|---|---|
| 1 | 5 | Entropy | 15 | 9 | 5 | 2 |
| 2 | 500 | Entropy | 15 | 14 | 5 | 7 |
| 3 | 5 | Entropy | 1 | 8 | 5 | 2 |
| 4 | 97 | Entropy | 4 | 3 | 13 | 15 |
| 5 | 500 | Gini | 4 | 6 | 5 | 2 |
| 6 | 500 | Gini | 15 | 1 | 5 | 2 |
| 7 | 500 | Gini | 15 | 1 | 5 | 2 |
| 8 | 462 | Entropy | 6 | 4 | 8 | 5 |
| 9 | 61 | Gini | 15 | 3 | 7 | 12 |
| 10 | 500 | Gini | 15 | 1 | 5 | 2 |
| Dataset # | Five-Fold Cv Accuracy | F1-Score | AUROC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Default | BO | BO-ML | Default | BO | BO-ML | Default | BO | BO-ML | |
| 1 | 0.777 | 0.833 | 0.792 | 0.829 | 0.848 | 0.864 | 0.819 | 0.847 | 0.834 |
| 2 | 0.774 | 0.781 | 0.811 | 0.813 | 0.875 | 0.850 | 0.813 | 0.876 | 0.850 |
| 3 | 0.754 | 0.825 | 0.799 | 0.758 | 0.864 | 0.803 | 0.768 | 0.864 | 0.813 |
| 4 | 0.723 | 0.800 | 0.740 | 0.800 | 0.875 | 0.817 | 0.800 | 0.875 | 0.817 |
| 5 | 0.769 | 0.874 | 0.785 | 0.794 | 0.882 | 0.810 | 0.794 | 0.881 | 0.810 |
| 6 | 0.776 | 0.822 | 0.799 | 0.802 | 0.869 | 0.825 | 0.801 | 0.868 | 0.824 |
| 7 | 0.625 | 0.797 | 0.704 | 0.696 | 0.869 | 0.775 | 0.697 | 0.869 | 0.776 |
| 8 | 0.747 | 0.837 | 0.792 | 0.771 | 0.872 | 0.816 | 0.771 | 0.859 | 0.816 |
| 9 | 0.699 | 0.775 | 0.738 | 0.751 | 0.834 | 0.790 | 0.750 | 0.826 | 0.789 |
| 10 | 0.725 | 0.811 | 0.775 | 0.821 | 0.882 | 0.871 | 0.816 | 0.882 | 0.866 |
| Mean | 0.737 | 0.815 | 0.773 | 0.783 | 0.867 | 0.822 | 0.783 | 0.865 | 0.819 |
| Dataset # | Five-Fold Cv Accuracy | F1-Score | AUROC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Default | BO | BO-ML | Default | BO | BO-ML | Default | BO | BO-ML | |
| 1 | 0.714 | 0.817 | 0.771 | 0.754 | 0.825 | 0.775 | 0.854 | 0.917 | 0.871 |
| 2 | 0.718 | 0.792 | 0.751 | 0.750 | 0.825 | 0.800 | 0.855 | 0.944 | 0.909 |
| 3 | 0.700 | 0.800 | 0.760 | 0.792 | 0.890 | 0.797 | 0.792 | 0.829 | 0.808 |
| 4 | 0.708 | 0.778 | 0.783 | 0.782 | 0.831 | 0.812 | 0.776 | 0.864 | 0.800 |
| 5 | 0.757 | 0.800 | 0.771 | 0.771 | 0.837 | 0.781 | 0.783 | 0.844 | 0.783 |
| 6 | 0.700 | 0.708 | 0.700 | 0.700 | 0.814 | 0.799 | 0.725 | 0.833 | 0.817 |
| 7 | 0.800 | 0.814 | 0.800 | 0.792 | 0.814 | 0.792 | 0.792 | 0.809 | 0.792 |
| 8 | 0.662 | 0.708 | 0.692 | 0.778 | 0.816 | 0.821 | 0.718 | 0.817 | 0.773 |
| 9 | 0.744 | 0.808 | 0.763 | 0.792 | 0.814 | 0.807 | 0.786 | 0.809 | 0.807 |
| 10 | 0.708 | 0.752 | 0.738 | 0.724 | 0.783 | 0.744 | 0.724 | 0.835 | 0.824 |
| Mean | 0.721 | 0.777 | 0.753 | 0.763 | 0.825 | 0.793 | 0.780 | 0.850 | 0.818 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, B.; Sameen, M.I.; Al-Najjar, H.A.H.; Sheng, D.; Alamri, A.M.; Park, H.-J. A Meta-Learning Approach of Optimisation for Spatial Prediction of Landslides. Remote Sens. 2021, 13, 4521. https://doi.org/10.3390/rs13224521
Pradhan B, Sameen MI, Al-Najjar HAH, Sheng D, Alamri AM, Park H-J. A Meta-Learning Approach of Optimisation for Spatial Prediction of Landslides. Remote Sensing. 2021; 13(22):4521. https://doi.org/10.3390/rs13224521
Chicago/Turabian StylePradhan, Biswajeet, Maher Ibrahim Sameen, Husam A. H. Al-Najjar, Daichao Sheng, Abdullah M. Alamri, and Hyuck-Jin Park. 2021. "A Meta-Learning Approach of Optimisation for Spatial Prediction of Landslides" Remote Sensing 13, no. 22: 4521. https://doi.org/10.3390/rs13224521
APA StylePradhan, B., Sameen, M. I., Al-Najjar, H. A. H., Sheng, D., Alamri, A. M., & Park, H. -J. (2021). A Meta-Learning Approach of Optimisation for Spatial Prediction of Landslides. Remote Sensing, 13(22), 4521. https://doi.org/10.3390/rs13224521