Monitoring Forest Health Using Hyperspectral Imagery: Does Feature Selection Improve the Performance of Machine-Learning Techniques?
Abstract
:1. Introduction
- How do different feature selection methods influence the predictive performance of ML models of the defoliation of trees?
- Do different (environmental) feature sets show differences in performance?
- Can predictive performance be substantially improved by combining feature sets?
- Which features are most important and how can these be interpreted in this context?
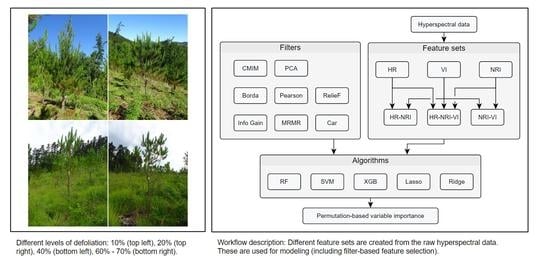
2. Materials and Methods
2.1. Data and Study Area
2.1.1. In Situ Data
2.1.2. Hyperspectral Data
2.2. Derivation of Indices
2.3. Feature Selection
2.3.1. Filter Methods
2.3.2. Description of Used Filter Methods
- Univariate/multivariate (scoring based on a single variable/multiple variables).
- Linear/non-linear (usage of linear/non-linear calculations).
- Entropy/correlation (scoring based on derivations of entropy or correlation-based approaches).
2.4. Benchmarking Design
2.4.1. Algorithms
- Extreme gradient boosting (XGBoost);
- Random forest (RF);
- Penalized regression (with L1/lasso and L2/ridge penalties);
- Support vector machine (SVM, radial basis function Kernel);
- Featureless learner.
2.4.2. Feature Sets
- The raw hyperspectral band information (HR): no feature engineering;
- Vegetation indices (vegetation index (VI)s): expert-based feature engineering;
- Normalized ratio indices (NRIs): data-driven feature engineering.
- HR + VI
- HR + NRI;
- HR + VI + NRI.
2.4.3. Hyperparameter Optimization
2.4.4. Spatial Resampling
2.5. Feature Importance and Feature Effects
2.6. Research Compendium
3. Results
3.1. Principal Component Analysis of Feature Sets
3.2. Predictive Performance
3.3. Variable Importance
Permutation-Based Variable Importance
4. Discussion
4.1. Predictive Performance
4.1.1. Model Differences
4.1.2. Feature Set Differences
4.2. Performance vs. Plot Characteristics
4.3. Feature Selection Methods
4.4. Linking Feature Importance to Spectral Characteristics
4.5. Data Quality
4.6. Practical Implications on Defoliation and Tree Health Mapping
4.7. Comparison to Other Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | above-ground biomass |
| ALE | accumulated local effects |
| ALS | airborne laser scanning |
| ANN | artificial neural network |
| AUROC | area under the receiver operating characteristics curve |
| BRT | boosted regression trees |
| CART | classification and regression trees |
| CNN | convolutional neural networks |
| CV | cross-validation |
| DAP | digital aerial photogrammetry |
| ENM | environmental niche modeling |
| FFS | forward feature selection |
| FPR | false positive rate |
| FS | feature selection |
| GAM | generalized additive model |
| GBM | gradient boosting machine |
| GLM | generalized linear model |
| ICGC | Institut Cartografic i Geologic de Catalunya |
| IQR | interquartile range |
| LiDAR | light detection and ranging |
| LOWESS | locally weighted scatter plot smoothing |
| MARS | multivariate adaptive regression splines |
| MBO | model-based optimization |
| MEM | maximum entropy model |
| ML | machine learning |
| NDII | normalized difference infrared index |
| NDMI | normalized difference moisture index |
| NIR | near-infrared |
| NRI | normalized ratio index |
| OLS | ordinary least squares |
| OMNBR | optimized multiple narrow-band reflectance |
| PCA | principal component analysis |
| PDP | partial dependence plots |
| PISR | potential incoming solar radiation |
| PLS | partial least-squares |
| POV | proportion of variance explained |
| RBF | radial basis function |
| RF | random forest |
| RMSE | root mean square error |
| RR | ridge regression |
| RSS | residual sum of squares |
| SAR | synthetic aperture radar |
| SDM | species distribution modeling |
| SMBO | sequential-based model optimization |
| SVM | support vector machine |
| TPR | true positive rate |
| VI | vegetation index |
| XGBoost | extreme gradient boosting |
Appendix A
Appendix A.1

Appendix A.2
| Model (Package) | Hyperparameter | Type | Start | End | Default |
|---|---|---|---|---|---|
| RF (ranger) | dbl | 0 | 0.5 | - | |
| min.node.size | int | 1 | 10 | 1 | |
| sample.fraction | dbl | 0.2 | 0.9 | 1 | |
| SVM (kernlab) | C | dbl | 1 | ||
| dbl | 1 | ||||
| XGBoost (xgboost) | nrounds | int | 10 | 70 | - |
| colsample_bytree | dbl | 0.6 | 1 | 1 | |
| subsample | dbl | 0.6 | 1 | 1 | |
| max_depth | int | 3 | 15 | 6 | |
| gamma | int | 0.05 | 10 | 0 | |
| eta | dbl | 0.1 | 1 | 0.3 | |
| min_child_weight | int | 1 | 7 | 1 |
Appendix A.3
| Name | Formula | Reference |
|---|---|---|
| Boochs | [98] | |
| Boochs2 | [98] | |
| CAI | [99] | |
| CARI | [100] | |
| Carter | [101] | |
| Carter2 | [101] | |
| Carter3 | [101] | |
| Carter4 | [101] | |
| Carter5 | [101] | |
| Carter6 | [101] | |
| CI | [102] | |
| CI 2 | [103] | |
| ClAInt | [104] | |
| CRI1 | [103] | |
| CRI2 | [103] | |
| CRI3 | [103] | |
| CRI4 | [103] | |
| D1 | [102] | |
| D2 | [102] | |
| Datt | [105] | |
| Datt2 | [105] | |
| Datt3 | [105] | |
| Datt4 | [106] | |
| Datt5 | [106] | |
| Datt6 | [106] | |
| Datt7 | [107] | |
| Datt8 | [107] | |
| DD | [108] | |
| DDn | [109] | |
| DPI | [102] | |
| DWSI1 | [110] | |
| DWSI2 | [110] | |
| DWSI3 | [110] | |
| DWSI4 | [110] | |
| DWSI5 | [110] | |
| EGFN | [111] | |
| EGFR | [111] | |
| EVI | [112] | |
| GDVI | [113] | |
| GI | [114] | |
| Gitelson | [115] | |
| Gitelson2 | [103] | |
| GMI1 | [103] | |
| GMI2 | [103] | |
| Green NDVI | [116] | |
| LWVI_1 | [117] | |
| LWVI_2 | [117] | |
| Maccioni | [118] | |
| MCARI | [119] | |
| MCARI2 | [120] | |
| mND705 | [121] | |
| mNDVI | [121] | |
| MPRI | [122] | |
| MSAVI | [123] | |
| MSI | [124] | |
| mSR | [121] | |
| mSR2 | [125] | |
| mSR705 | [121] | |
| MTCI | [126] | |
| MTVI | [127] | |
| NDLI | [128] | |
| NDNI | [128] | |
| NDVI | [129] | |
| NDVI2 | [130] | |
| NDVI3 | [131] | |
| NDWI | [73] | |
| NPCI | [111] | |
| OSAVI | [132] | |
| OSAVI2 | [120] | |
| PARS | [133] | |
| PRI | [134] | |
| PRI_norm | [135] | |
| PRI ∗ CI2 | [136] | |
| PSRI | [137] | |
| PSSR | [138] | |
| PSND | [138] | |
| PWI | [139] | |
| RDVI | [140] | |
| REP_LE | Red-edge position through linear extrapolation | [141] |
| REP_Li | [142] | |
| SAVI | [143] | |
| SIPI | [144] | |
| SPVI | [145] | |
| SR | [146] | |
| SR1 | [147] | |
| SR2 | [147] | |
| SR3 | [147] | |
| SR4 | [148] | |
| SR5 | [133] | |
| SR6 | [149] | |
| SR7 | [150] | |
| SR8 | [151] | |
| SRPI | [144] | |
| SRWI | [102] | |
| Sum_Dr1 | [152] | |
| Sum_Dr2 | [153] | |
| SWIR FI | [154] | |
| SWIR LI | [155] | |
| SWIR SI | [155] | |
| SWIR VI | [155] | |
| TCARI | [127] | |
| TCARI/OSAVI | TCARI/OSAVI | [127] |
| TCARI2 | [120] | |
| TCARI2/OSAVI2 | TCARI2/OSAVI2 | [120] |
| TGI | [156] | |
| TVI | [157] | |
| Vogelmann | [97] | |
| Vogelmann2 | [97] | |
| Vogelmann3 | [97] | |
| Vogelmann4 | [97] |
Appendix A.4
References
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine Learning in Geosciences and Remote Sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote Sensing Big Data Computing: Challenges and Opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Mascaro, J.; Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Martin, R.E.; Anderson, C.; Higgins, M.; Chadwick, K.D. A Tale of Two “Forests”: Random Forest Machine Learning Aids Tropical Forest Carbon Mapping. PLoS ONE 2014, 9, e85993. [Google Scholar] [CrossRef]
- Urban, M.; Berger, C.; Mudau, T.E.; Heckel, K.; Truckenbrodt, J.; Onyango Odipo, V.; Smit, I.P.J.; Schmullius, C. Surface Moisture and Vegetation Cover Analysis for Drought Monitoring in the Southern Kruger National Park Using Sentinel-1, Sentinel-2, and Landsat-8. Remote Sens. 2018, 10, 1482. [Google Scholar] [CrossRef] [Green Version]
- Hawryło, P.; Bednarz, B.; Wezyk, P.; Szostak, M. Estimating Defoliation of Scots Pine Stands Using Machine Learning Methods and Vegetation Indices of Sentinel-2. Eur. J. Remote Sens. 2018, 51, 194–204. [Google Scholar] [CrossRef] [Green Version]
- Pollastrini, M.; Feducci, M.; Bonal, D.; Fotelli, M.; Gessler, A.; Grossiord, C.; Guyot, V.; Jactel, H.; Nguyen, D.; Radoglou, K.; et al. Physiological Significance of Forest Tree Defoliation: Results from a Survey in a Mixed Forest in Tuscany (Central Italy). For. Ecol. Manag. 2016, 361, 170–178. [Google Scholar] [CrossRef]
- Gottardini, E.; Cristofolini, F.; Cristofori, A.; Pollastrini, M.; Camin, F.; Ferretti, M. A Multi-Proxy Approach Reveals Common and Species-Specific Features Associated with Tree Defoliation in Broadleaved Species. For. Ecol. Manag. 2020, 467, 118151. [Google Scholar] [CrossRef]
- Oliva, J.; Stenlid, J.; Grönkvist-Wichmann, L.; Wahlström, K.; Jonsson, M.; Drobyshev, I.; Stenström, E. Pathogen-Induced Defoliation of Pinus Sylvestris Leads to Tree Decline and Death from Secondary Biotic Factors. For. Ecol. Manag. 2016, 379, 273–280. [Google Scholar] [CrossRef]
- Zhang, K.; Thapa, B.; Ross, M.; Gann, D. Remote Sensing of Seasonal Changes and Disturbances in Mangrove Forest: A Case Study from South Florida. Ecosphere 2016, 7, e01366. [Google Scholar] [CrossRef] [Green Version]
- Townsend, P.A.; Singh, A.; Foster, J.R.; Rehberg, N.J.; Kingdon, C.C.; Eshleman, K.N.; Seagle, S.W. A General Landsat Model to Predict Canopy Defoliation in Broadleaf Deciduous Forests. Remote Sens. Environ. 2012, 119, 255–265. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, T.; de Bie, C.A.J.M.; Skidmore, A.K.; Liu, X.; Song, S.; Zhang, L.; Wang, J.; Shao, X. Satellite-Derived Vegetation Indices Contribute Significantly to the Prediction of Epiphyllous Liverworts. Ecol. Indic. 2014, 38, 72–80. [Google Scholar] [CrossRef]
- Adamczyk, J.; Osberger, A. Red-Edge Vegetation Indices for Detecting and Assessing Disturbances in Norway Spruce Dominated Mountain Forests. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 90–99. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. (Eds.) Hyperspectral Indices and Image Classifications for Agriculture and Vegetation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature Selection in Machine Learning: A New Perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Pinto, J.; Powell, S.; Peterson, R.; Rosalen, D.; Fernandes, O. Detection of Defoliation Injury in Peanut with Hyperspectral Proximal Remote Sensing. Remote Sens. 2020, 12, 3828. [Google Scholar] [CrossRef]
- Yu, R.; Ren, L.; Luo, Y. Early Detection of Pine Wilt Disease in Pinus Tabuliformis in North China Using a Field Portable Spectrometer and UAV-Based Hyperspectral Imagery. For. Ecosyst. 2021, 8, 44. [Google Scholar] [CrossRef]
- Lin, H.; Yan, E.; Wang, G.; Song, R. Analysis of Hyperspectral Bands for the Health Diagnosis of Tree Species. In Proceedings of the 2014 Third International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014; pp. 448–451. [Google Scholar] [CrossRef]
- Kayet, N.; Pathak, K.; Chakrabarty, A.; Singh, C.P.; Chowdary, V.M.; Kumar, S.; Sahoo, S. Forest Health Assessment for Geo-Environmental Planning and Management in Hilltop Mining Areas Using Hyperion and Landsat Data. Ecol. Indic. 2019, 106, 105471. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing Very High Resolution UAV Imagery for Monitoring Forest Health during a Simulated Disease Outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Trunk, G.V. A Problem of Dimensionality: A Simple Example. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 306–307. [Google Scholar] [CrossRef]
- Xu, H.; Caramanis, C.; Mannor, S. Statistical Optimization in High Dimensions. Oper. Res. 2016, 64, 958–979. [Google Scholar] [CrossRef] [Green Version]
- Mesanza, N.; Iturritxa, E.; Patten, C.L. Native Rhizobacteria as Biocontrol Agents of Heterobasidion Annosum s.s. and Armillaria Mellea Infection of Pinus Radiata. Biol. Control 2016, 101, 8–16. [Google Scholar] [CrossRef]
- Iturritxa, E.; Trask, T.; Mesanza, N.; Raposo, R.; Elvira-Recuenco, M.; Patten, C.L. Biocontrol of Fusarium Circinatum Infection of Young Pinus Radiata Trees. Forests 2017, 8, 32. [Google Scholar] [CrossRef] [Green Version]
- Iturritxa, E.; Mesanza, N.; Brenning, A. Spatial Analysis of the Risk of Major Forest Diseases in Monterey Pine Plantations. Plant Pathol. 2014, 64, 880–889. [Google Scholar] [CrossRef]
- Ganley, R.J.; Watt, M.S.; Manning, L.; Iturritxa, E. A Global Climatic Risk Assessment of Pitch Canker Disease. Can. J. For. Res. 2009, 39, 2246–2256. [Google Scholar] [CrossRef]
- Innes, J. Methods to Estimate Forest Health. Silva Fenn. 1993, 27. [Google Scholar] [CrossRef] [Green Version]
- MacLean, D.A.; Lidstone, R.G. Defoliation by Spruce Budworm: Estimation by Ocular and Shoot-Count Methods and Variability among Branches, Trees, and Stands. Can. J. For. Res. 1982, 12, 582–594. [Google Scholar] [CrossRef]
- Johnstone, I.M.; Titterington, D.M. Statistical Challenges of High-Dimensional Data. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 4237–4253. [Google Scholar] [CrossRef] [Green Version]
- Bommert, A.; Sun, X.; Bischl, B.; Rahnenführer, J.; Lang, M. Benchmark for Filter Methods for Feature Selection in High-Dimensional Classification Data. Comput. Stat. Data Anal. 2020, 143, 106839. [Google Scholar] [CrossRef]
- Das, S. Filters, Wrappers and a Boosting-Based Hybrid for Feature Selection; ICML, Citeseer: University Park, PA, USA, 2001. [Google Scholar]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Jolliffe, I.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Drotár, P.; Šimoňák, S.; Pietriková, E.; Chovanec, M.; Chovancová, E.; Ádám, N.; Szabó, C.; Baláž, A.; Biňas, M. Comparison of Filter Techniques for Two-Step Feature Selection. Comput. Inform. 2017, 36, 597–617. [Google Scholar] [CrossRef]
- Drotár, P.; Gazda, J.; Smékal, Z. An Experimental Comparison of Feature Selection Methods on Two-Class Biomedical Datasets. Comput. Biol. Med. 2015, 66, 1–10. [Google Scholar] [CrossRef]
- Abeel, T.; Helleputte, T.; Van de Peer, Y.; Dupont, P.; Saeys, Y. Robust Biomarker Identification for Cancer Diagnosis with Ensemble Feature Selection Methods. Bioinformatics 2010, 26, 392–398. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Proceedings of the First International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Polikar, R. Ensemble Learning. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: Boston, MA, USA, 2012; pp. 1–34. [Google Scholar] [CrossRef]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.; Blum, M.; Hutter, F. Efficient and Robust Automated Machine Learning. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2015; pp. 2962–2970. [Google Scholar]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for Feature Selection: A Review and Future Trends. Inf. Fusion 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On Lines and Planes of Closest Fit to Systems of Points in Space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.M. Maximum Relevance/Minimum Redundancy (MRMR). In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013; pp. 1191–1192. [Google Scholar] [CrossRef]
- Zuber, V.; Strimmer, K. High-Dimensional Regression and Variable Selection Using CAR Scores. Stat. Appl. Genet. Mol. Biol. 2011, 10, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Kira, K.; Rendell, L.A. The Feature Selection Problem: Traditional Methods and a New Algorithm. In Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; AAAI Press: Menlo Park, CA, USA, 1992; pp. 129–134. [Google Scholar]
- Fleuret, F. Fast Binary Feature Selection with Conditional Mutual Information. J. Mach. Learn. Res. 2004, 5, 1531–1555. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Friedman, J.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Peña, M.; Liao, R.; Brenning, A. Using Spectrotemporal Indices to Improve the Fruit-Tree Crop Classification Accuracy. ISPRS J. Photogramm. Remote Sens. 2017, 128, 158–169. [Google Scholar] [CrossRef]
- Bischl, B.; Richter, J.; Bossek, J.; Horn, D.; Thomas, J.; Lang, M. mlrMBO: A Modular Framework for Model-Based Optimization of Expensive Black-Box Functions. arXiv 2017, arXiv:1703.03373. [Google Scholar]
- Binder, M.; Moosbauer, J.; Thomas, J.; Bischl, B. Multi-Objective Hyperparameter Tuning and Feature Selection Using Filter Ensembles. arXiv 2020, arXiv:1912.12912. [Google Scholar]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter Tuning and Performance Assessment of Statistical and Machine-Learning Algorithms Using Spatial Data. Ecol. Model. 2019, 406, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-Based Optimization for General Algorithm Configuration; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar] [CrossRef] [Green Version]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Brenning, A. Spatial Cross-Validation and Bootstrap for the Assessment of Prediction Rules in Remote Sensing: The R Package Sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; R Package Version 2.1.0. IEEE: Toulouse, France, 2012. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Greenwell, B.M.; Boehmke, B.C.; McCarthy, A.J. A Simple and Effective Model-Based Variable Importance Measure. arXiv 2018, arXiv:1805.04755. [Google Scholar]
- Molnar, C. Interpretable Machine Learning—A Guide for Making Black Box Models Explainable; Self-Published: Munich, Germany, 2019. [Google Scholar]
- Brenning, A. Transforming Feature Space to Interpret Machine Learning Models. arXiv 2021, arXiv:2104.04295. [Google Scholar]
- Apley, D.W.; Zhu, J. Visualizing the Effects of Predictor Variables in Black Box Supervised Learning Models. arXiv 2019, arXiv:1612.08468. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. Kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kursa, M.B. Praznik: Collection of Information-Based Feature Selection Filters; R Package Vignette: Madison, WI, USA, 2018. [Google Scholar]
- Zawadzki, Z.; Kosinski, M. FSelectorRcpp: ‘Rcpp’ Implementation of ‘FSelector’ Entropy-Based Feature Selection Algorithms with a Sparse Matrix Support; R Package Vignette: Madison, WI, USA, 2019. [Google Scholar]
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. mlr: Machine learning in R. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- Landau, W.M. The drake R Package: A Pipeline Toolkit for Reproducibility and High-Performance Computing. J. Open Source Softw. 2018, 3, 550. [Google Scholar] [CrossRef]
- Ghosh, M.; Adhikary, S.; Ghosh, K.K.; Sardar, A.; Begum, S.; Sarkar, R. Genetic Algorithm Based Cancerous Gene Identification from Microarray Data Using Ensemble of Filter Methods. Med. Biol. Eng. Comput. 2019, 57, 159–176. [Google Scholar] [CrossRef] [PubMed]
- Horler, D.N.H.; Dockray, M.; Barber, J. The Red Edge of Plant Leaf Reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Hais, M.; Hellebrandová, K.N.; Šrámek, V. Potential of Landsat Spectral Indices in Regard to the Detection of Forest Health Changes Due to Drought Effects. J. For. Sci. 2019, 65, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.C. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Lehnert, L.W.; Meyer, H.; Bendix, J. Hsdar: Manage, Analyse and Simulate Hyperspectral Data in R; R Package Vignette: Madison, WI, USA, 2016. [Google Scholar]
- de Beurs, K.M.; Townsend, P.A. Estimating the Effect of Gypsy Moth Defoliation Using MODIS. Remote Sens. Environ. 2008, 112, 3983–3990. [Google Scholar] [CrossRef]
- Rengarajan, R.; Schott, J.R. Modeling Forest Defoliation Using Simulated BRDF and Assessing Its Effect on Reflectance and Sensor Reaching Radiance. In Remote Sensing and Modeling of Ecosystems for Sustainability XIII; International Society for Optics and Photonics: San Diego, CA, USA, 2016; Volume 9975, p. 997503. [Google Scholar] [CrossRef]
- Meng, R.; Dennison, P.E.; Zhao, F.; Shendryk, I.; Rickert, A.; Hanavan, R.P.; Cook, B.D.; Serbin, S.P. Mapping Canopy Defoliation by Herbivorous Insects at the Individual Tree Level Using Bi-Temporal Airborne Imaging Spectroscopy and LiDAR Measurements. Remote Sens. Environ. 2018, 215, 170–183. [Google Scholar] [CrossRef]
- Kälin, U.; Lang, N.; Hug, C.; Gessler, A.; Wegner, J.D. Defoliation Estimation of Forest Trees from Ground-Level Images. Remote Sens. Environ. 2019, 223, 143–153. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Hermosilla, T.; Tompalski, P.; McCartney, G.; MacLean, D.A. Digital Aerial Photogrammetry for Assessing Cumulative Spruce Budworm Defoliation and Enhancing Forest Inventories at a Landscape-Level. ISPRS J. Photogramm. Remote Sens. 2018, 142, 1–11. [Google Scholar] [CrossRef]
- Hlebarska, S.; Georgieva, M. Distribution of the invasive pathogen Diplodia sapinea on Pinus spp. in Bulgaria. In Proceedings of the 90 Years Forest Research Institute—For the Society and Nature, Sofia, Bulgaria, 24–26 October 2018; pp. 61–70. [Google Scholar]
- Kaya, A.G.A.; Yeltekin, Ş.; Lehtijarvi, T.D.; Lehtijarvi, A.; Woodward, S. Severity of Diplodia Shoot Blight (Caused by Diplodia Sapinea) Was Greatest on Pinus Sylvestris and Pinus Nigra in a Plantation Containing Five Pine Species. Phytopathol. Mediterr. 2019, 58, 249–259. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Xia, J.; Liao, W.; Chanussot, J.; Du, P.; Song, G.; Philips, W. Improving Random Forest with Ensemble of Features and Semisupervised Feature Extraction. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1471–1475. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Förster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of Feature Reduction Algorithms for Classifying Tree Species With Hyperspectral Data on Three Central European Test Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Unsupervised Feature Selection Based on Maximum Information and Minimum Redundancy for Hyperspectral Images. Pattern Recognit. 2016, 51, 295–309. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less Is More: Optimizing Classification Performance through Feature Selection in a Very-High-Resolution Remote Sensing Object-Based Urban Application. GISci. Remote Sens. 2018, 55, 221–242. [Google Scholar] [CrossRef]
- Rochac, J.F.R.; Zhang, N. Feature Extraction in Hyperspectral Imaging Using Adaptive Feature Selection Approach. In Proceedings of the 2016 Eighth International Conference on Advanced Computational Intelligence (ICACI), Chiang Mai, Thailand, 14–16 February 2016; pp. 36–40. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature Selection for Classification of Hyperspectral Data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef] [Green Version]
- Keller, S.; Braun, A.C.; Hinz, S.; Weinmann, M. Investigation of the Impact of Dimensionality Reduction and Feature Selection on the Classification of Hyperspectral EnMAP Data. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Q.; Yin, K.; Zhang, F.; Liu, D.; Yang, G. Combining Random Forest and Support Vector Machines for Object-Based Rural-Land-Cover Classification Using High Spatial Resolution Imagery. J. Appl. Remote Sens. 2019, 13, 014521. [Google Scholar] [CrossRef]
- Shendryk, I.; Broich, M.; Tulbure, M.G.; McGrath, A.; Keith, D.; Alexandrov, S.V. Mapping Individual Tree Health Using Full-Waveform Airborne Laser Scans and Imaging Spectroscopy: A Case Study for a Floodplain Eucalypt Forest. Remote Sens. Environ. 2016, 187, 202–217. [Google Scholar] [CrossRef]
- Ludwig, M.; Morgenthal, T.; Detsch, F.; Higginbottom, T.P.; Lezama Valdes, M.; Nauß, T.; Meyer, H. Machine Learning and Multi-Sensor Based Modelling of Woody Vegetation in the Molopo Area, South Africa. Remote Sens. Environ. 2019, 222, 195–203. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving Performance of Spatio-Temporal Machine Learning Models Using Forward Feature Selection and Target-Oriented Validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Zandler, H.; Brenning, A.; Samimi, C. Quantifying Dwarf Shrub Biomass in an Arid Environment: Comparing Empirical Methods in a High Dimensional Setting. Remote Sens. Environ. 2015, 158, 140–155. [Google Scholar] [CrossRef]
- Guo, Y.; Chung, F.L.; Li, G.; Zhang, L. Multi-Label Bioinformatics Data Classification with Ensemble Embedded Feature Selection. IEEE Access 2019, 7, 103863–103875. [Google Scholar] [CrossRef]
- Radovic, M.; Ghalwash, M.; Filipovic, N.; Obradovic, Z. Minimum Redundancy Maximum Relevance Feature Selection Approach for Temporal Gene Expression Data. BMC Bioinform. 2017, 18, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red Edge Spectral Measurements from Sugar Maple Leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Boochs, F.; Kupfer, G.; Dockter, K.; Kühbauch, W. Shape of the Red Edge as Vitality Indicator for Plants. Int. J. Remote Sens. 1990, 11, 1741–1753. [Google Scholar] [CrossRef]
- Nagler, P.L.; Inoue, Y.; Glenn, E.P.; Russ, A.L.; Daughtry, C.S.T. Cellulose Absorption Index (CAI) to Quantify Mixed Soil–Plant Litter Scenes. Remote Sens. Environ. 2003, 87, 310–325. [Google Scholar] [CrossRef]
- Walthall, C.L.; Daughtry, C.S.T.; Chappelle, E.W.; Mcmurtrey, J.E.; Kim, M.S. The Use of High Spectral Resolution Bands for Estimating Absorbed Photosynthetically Active Radiation (A Par); NASA Gov: Washington, DC, USA, 1994.
- Carter, G.A. Ratios of Leaf Reflectances in Narrow Wavebands as Indicators of Plant Stress. Int. J. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-State Chlorophyll a Fluorescence Detection from Canopy Derivative Reflectance and Double-Peak Red-Edge Effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-Destructive Chlorophyll Assessment in Higher Plant Leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Oppelt, N.; Mauser, W. Hyperspectral Monitoring of Physiological Parameters of Wheat during a Vegetation Period Using AVIS Data. Int. J. Remote Sens. 2004, 25, 145–159. [Google Scholar] [CrossRef]
- Datt, B. Visible/near Infrared Reflectance and Chlorophyll Content in Eucalyptus Leaves. Int. J. Remote Sens. 1999, 20, 2741–2759. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Chlorophyll a, Chlorophyll b, Chlorophyll A+b, and Total Carotenoid Content in Eucalyptus Leaves. Remote Sens. Environ. 1998, 66, 111–121. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Water Content in Eucalyptus Leaves. Aust. J. Bot. 1999, 47, 909. [Google Scholar] [CrossRef]
- le Maire, G.; François, C.; Dufrêne, E. Towards Universal Broad Leaf Chlorophyll Indices Using PROSPECT Simulated Database and Hyperspectral Reflectance Measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Lemaire, G.; Francois, C.; Soudani, K.; Berveiller, D.; Pontailler, J.; Breda, N.; Genet, H.; Davi, H.; Dufrene, E. Calibration and Validation of Hyperspectral Indices for the Estimation of Broadleaved Forest Leaf Chlorophyll Content, Leaf Mass per Area, Leaf Area Index and Leaf Canopy Biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Apan, A.; Held, A.; Phinn, S.; Markley, J. Detecting Sugarcane `orange Rust’ Disease Using EO-1 Hyperion Hyperspectral Imagery. Int. J. Remote Sens. 2004, 25, 489–498. [Google Scholar] [CrossRef] [Green Version]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance Indices Associated with Physiological Changes in Nitrogen- and Water-Limited Sunflower Leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W. A Comparison of Vegetation Indices over a Global Set of TM Images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Wu, W. The Generalized Difference Vegetation Index (GDVI) for Dryland Characterization. Remote Sens. 2014, 6, 1211–1233. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.C.G.; Adams, J.; Stephens, D.J.; Hick, P.T. Forecasting Wheat Yield in a Mediterranean-Type Environment from the NOAA Satellite. Aust. J. Agric. Res. 1995, 46, 113. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Buschmann, C.; Lichtenthaler, H.K. The Chlorophyll Fluorescence Ratio F735/F700 as an Accurate Measure of the Chlorophyll Content in Plants. Remote Sens. Environ. 1999, 69, 296–302. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Galvão, L.S.; Formaggio, A.R.; Tisot, D.A. Discrimination of Sugarcane Varieties in Southeastern Brazil with EO-1 Hyperion Data. Remote Sens. Environ. 2005, 94, 523–534. [Google Scholar] [CrossRef]
- Maccioni, A.; Agati, G.; Mazzinghi, P. New Vegetation Indices for Remote Measurement of Chlorophylls Based on Leaf Directional Reflectance Spectra. J. Photochem. Photobiol. B Biol. 2001, 61, 52–61. [Google Scholar] [CrossRef]
- Daughtry, C. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating Chlorophyll Content from Hyperspectral Vegetation Indices: Modeling and Validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between Leaf Pigment Content and Spectral Reflectance across a Wide Range of Species, Leaf Structures and Developmental Stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Suárez, L.; Morales, F.; Zarco-Tejada, P.J. Assessing Structural Effects on PRI for Stress Detection in Conifer Forests. Remote Sens. Environ. 2011, 115, 2360–2375. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Hunt, E.; Rock, B. Detection of Changes in Leaf Water Content Using Near- and Middle-Infrared Reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote. Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P. Evaluation of the MERIS Terrestrial Chlorophyll Index (MTCI). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated Narrow-Band Vegetation Indices for Prediction of Crop Chlorophyll Content for Application to Precision Agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Serrano, L.; Peñuelas, J.; Ustin, S.L. Remote Sensing of Nitrogen and Lignin in Mediterranean Vegetation from AVIRIS Data. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.; Merzlyak, M.N. Quantitative Estimation of Chlorophyll-a Using Reflectance Spectra: Experiments with Autumn Chestnut and Maple Leaves. J. Photochem. Photobiol. B Biol. 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Guanter, L.; Alonso, L.; Moreno, J. A Method for the Surface Reflectance Retrieval from PROBA/CHRIS Data over Land: Application to ESA SPARC Campaigns. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2908–2917. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Chappelle, E.W.; Kim, M.S.; McMurtrey, J.E. Ratio Analysis of Reflectance Spectra (RARS): An Algorithm for the Remote Estimation of the Concentrations of Chlorophyll A, Chlorophyll B, and Carotenoids in Soybean Leaves. Remote Sens. Environ. 1992, 39, 239–247. [Google Scholar] [CrossRef]
- Gamon, J.; Peñuelas, J.; Field, C. A Narrow-Waveband Spectral Index That Tracks Diurnal Changes in Photosynthetic Efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suárez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A PRI-Based Water Stress Index Combining Structural and Chlorophyll Effects: Assessment Using Diurnal Narrow-Band Airborne Imagery and the CWSI Thermal Index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Garrity, S.R.; Eitel, J.U.; Vierling, L.A. Disentangling the Relationships between Plant Pigments and the Photochemical Reflectance Index Reveals a New Approach for Remote Estimation of Carotenoid Content. Remote Sens. Environ. 2011, 115, 628–635. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-Destructive Optical Detection of Pigment Changes during Leaf Senescence and Fruit Ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef] [Green Version]
- Blackburn, G.A. Quantifying Chlorophylls and Caroteniods at Leaf and Canopy Scales. Remote Sens. Environ. 1998, 66, 273–285. [Google Scholar] [CrossRef]
- Penuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of Plant Water Concentration by the Reflectance Water Index WI (R900/R970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K. A New Technique for Extracting the Red Edge Position from Hyperspectral Data: The Linear Extrapolation Method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F. Utilisation de La Haute Resolution Spectrale Pour Suivre l’etat Des Couverts Vegetaux. In Spectral Signatures of Objects in Remote Sensing; Guyenne, T.D., Hunt, J.J., Eds.; ESA Special Publication: Aussois, France, 1988; Volume 287, p. 279. [Google Scholar]
- Huete, A. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Lloret, P.; Munoz, F.; Vilaleliu, M. Reflectance Assessment of Mite Effects on Apple Trees. Int. J. Remote Sens. 1995, 16, 2727–2733. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. Angular Dependence of Maize and Sugar Beet VIs from Directional CHRIS/Proba Data. In Proceedings of the 4th ESA CHRIS PROBA Workshop, Frascati, Italy, 19–21 September 2006; Volume 2006, pp. 19–21. [Google Scholar]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote Estimation of Chlorophyll Content in Higher Plant Leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- McMurtrey, J.; Chappelle, E.; Kim, M.; Meisinger, J.; Corp, L. Distinguishing Nitrogen Fertilization Levels in Field Corn (Zea mays L.) with Actively Induced Fluorescence and Passive Reflectance Measurements. Remote Sens. Environ. 1994, 47, 36–44. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R. Land Cover Mapping at BOREAS Using Red Edge Spectral Parameters from CASI Imagery. J. Geophys. Res. Atmos. 1999, 104, 27921–27933. [Google Scholar] [CrossRef]
- Lichtenthaler, H.; Lang, M.; Sowinska, M.; Heisel, F.; Miehé, J. Detection of Vegetation Stress via a New High Resolution Fluorescence Imaging System. J. Plant Physiol. 1996, 148, 599–612. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Zarco-Tejada, P.J. Carotenoid Content Estimation in a Heterogeneous Conifer Forest Using Narrow-Band Indices and PROSPECTDART Simulations. Remote Sens. Environ. 2012, 127, 298–315. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Chen, Z. Comparison of Broad-Band and Narrow-Band Red and near-Infrared Vegetation Indices. Remote Sens. Environ. 1995, 54, 38–48. [Google Scholar] [CrossRef]
- Filella, I.; Penuelas, J. The Red Edge Position and Shape as Indicators of Plant Chlorophyll Content, Biomass and Hydric Status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Levin, N.; Kidron, G.J.; Ben-Dor, E. Surface Properties of Stabilizing Coastal Dunes: Combining Spectral and Field Analyses. Sedimentology 2007, 54, 771–788. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P.; Law, B.E.; Treuhaft, R.N. Subpixel Canopy Cover Estimation of Coniferous Forests in Oregon Using SWIR Imaging Spectrometry. J. Geophys. Res. Atmos. 2001, 106, 5151–5160. [Google Scholar] [CrossRef] [Green Version]
- Hunt, E.R.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.; Perry, E.M.; Akhmedov, B. A Visible Band Index for Remote Sensing Leaf Chlorophyll Content at the Canopy Scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef] [Green Version]
- Broge, N.; Leblanc, E. Comparing Prediction Power and Stability of Broadband and Hyperspectral Vegetation Indices for Estimation of Green Leaf Area Index and Canopy Chlorophyll Density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]






| Characteristic | Value |
|---|---|
| Geometric resolution | 1 m |
| Radiometric resolution | 12 bit |
| Spectral resolution | 126 bands (404.08–996.31 nm) |
| Correction: | Radiometric, geometric, atmospheric |
| Name | Group | Ref. |
|---|---|---|
| Linear correlation (Pearson) | univariate, linear, correlation | [41] |
| Information gain | univariate, non-linear, entropy | [42] |
| Minimum redundancy, maximum relevance | multivariate, non-linear, entropy | [43] |
| Carscore | multivariate, linear, correlation | [44] |
| Relief | multivariate, linear, entropy | [45] |
| Conditional minimal information maximization | multivariate, linear, entropy | [46] |
| Task | Model | Filter | RMSE | SE | |
|---|---|---|---|---|---|
| 1 | NRI-VI | SVM | Info Gain | 27.915 | 18.970 |
| 2 | NRI | RF | Relief | 30.842 | 12.028 |
| 3 | HR | XGBoost | Info Gain | 31.165 | 15.025 |
| 4 | NRI | Lasso-MBO | No Filter | 31.165 | 15.025 |
| 5 | NRI | Ridge-MBO | No Filter | 31.165 | 15.025 |
| 6 | - | regr.featureless | No Filter | 31.165 | 15.025 |
| RMSE | Test Plot | |
|---|---|---|
| 1 | 28.12 | Laukiz1 |
| 2 | 54.26 | Laukiz2 |
| 3 | 9.00 | Luiando |
| 4 | 21.17 | Oiartzun |
| Task | Model | Filter | RMSE | SE | |
|---|---|---|---|---|---|
| 1 | NRI-VI | SVM | Info Gain | 27.915 | 18.970 |
| 2 | NRI | SVM | CMIM | 28.044 | 19.101 |
| 3 | VI | SVM | Relief | 28.082 | 19.140 |
| 4 | NRI-VI | SVM | Borda | 28.102 | 19.128 |
| 5 | HR | SVM | CMIM | 28.119 | 19.123 |
| 6 | HR | SVM | MRMR | 28.119 | 19.123 |
| 7 | VI | SVM | Info Gain | 28.121 | 19.123 |
| 8 | NRI | SVM | PCA | 28.121 | 19.123 |
| 9 | HR-NRI | SVM | PCA | 28.121 | 19.123 |
| 10 | HR-NRI-VI | SVM | PCA | 28.121 | 19.123 |
| Task | Model | Filter | RMSE | SE | |
|---|---|---|---|---|---|
| 1 | VI | XGBoost | No Filter | 45.366 | 6.672 |
| 2 | HR | XGBoost | No Filter | 44.982 | 5.378 |
| 3 | VI | XGBoost | PCA | 44.539 | 8.187 |
| 4 | HR | XGBoost | PCA | 44.032 | 6.183 |
| 5 | NRI | XGBoost | PCA | 43.433 | 9.543 |
| 6 | HR-NRI | XGBoost | PCA | 43.220 | 2.557 |
| 7 | HR-NRI-VI | XGBoost | PCA | 41.076 | 9.862 |
| 8 | VI | RF | CMIM | 39.980 | 10.144 |
| 9 | VI | RF | Info Gain | 39.623 | 10.616 |
| 10 | NRI | XGBoost | Pearson | 39.492 | 11.548 |
| Learner | Test Plot | Features (%) | Features (#) |
|---|---|---|---|
| RF Car | Laukiz1 | 0.00245 | 1/1249 |
| Laukiz2 | 0.00359 | 1/1357 | |
| Luiando | 0.12448 | 2/1507 | |
| Oiartzun | 2.80356 | 37/1311 | |
| SVM Car | Laukiz1 | 16.76686 | 210/1249 |
| Laukiz2 | 40.77700 | 554/1357 | |
| Luiando | 43.80604 | 661/1507 | |
| Oiartzun | 81.23205 | 1065/1311 | |
| XGB Borda | Laukiz1 | 79.54091 | 994/1249 |
| Laukiz2 | 0.96545 | 14/1357 | |
| Luiando | 66.27871 | 999/1507 | |
| Oiartzun | 41.89759 | 550/1311 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schratz, P.; Muenchow, J.; Iturritxa, E.; Cortés, J.; Bischl, B.; Brenning, A. Monitoring Forest Health Using Hyperspectral Imagery: Does Feature Selection Improve the Performance of Machine-Learning Techniques? Remote Sens. 2021, 13, 4832. https://doi.org/10.3390/rs13234832
Schratz P, Muenchow J, Iturritxa E, Cortés J, Bischl B, Brenning A. Monitoring Forest Health Using Hyperspectral Imagery: Does Feature Selection Improve the Performance of Machine-Learning Techniques? Remote Sensing. 2021; 13(23):4832. https://doi.org/10.3390/rs13234832
Chicago/Turabian StyleSchratz, Patrick, Jannes Muenchow, Eugenia Iturritxa, José Cortés, Bernd Bischl, and Alexander Brenning. 2021. "Monitoring Forest Health Using Hyperspectral Imagery: Does Feature Selection Improve the Performance of Machine-Learning Techniques?" Remote Sensing 13, no. 23: 4832. https://doi.org/10.3390/rs13234832
APA StyleSchratz, P., Muenchow, J., Iturritxa, E., Cortés, J., Bischl, B., & Brenning, A. (2021). Monitoring Forest Health Using Hyperspectral Imagery: Does Feature Selection Improve the Performance of Machine-Learning Techniques? Remote Sensing, 13(23), 4832. https://doi.org/10.3390/rs13234832