PolSAR Image Classification Using a Superpixel-Based Composite Kernel and Elastic Net
Abstract
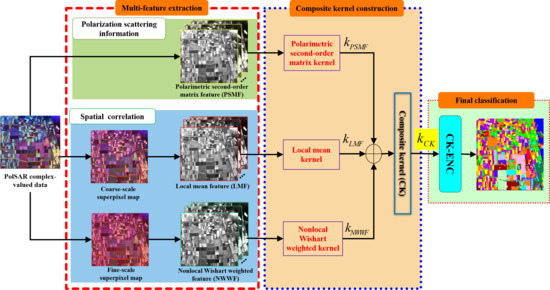
:1. Introduction
- Based on superpixel segmentation of different scales, a multi-feature extraction strategy is proposed. It can fully mine the inherent characteristics of PolSAR data and capture more discriminative information, thereby preserving the target contour and suppressing the speckles to improve the visual coherence of the classification maps.
- A composite kernel (CK) is constructed to implement the feature fusion and obtain a richer feature representation. The CK can well reflect the properties of PolSAR data hidden in the high dimensional feature space and effectively fuse multiple sources of information, thereby improving the representation and discrimination capabilities of features.
- The CK-ENC is proposed for the final PolSAR image classification. CK-ENC employs ENC to estimate more robust weight coefficients for pixel labeling, thereby achieving more accurate classification, especially for the condition of limited training samples.
2. Proposed Method
2.1. Multi-Feature Extraction
2.1.1. Polarimetric Second-Order Matrix Feature
2.1.2. Local Mean Feature within Coarse-Scale Superpixels
2.1.3. Nonlocal Wishart Weighted Feature among Fine-Scale Superpixels
2.2. Composite Kernel (CK) Construction
2.3. Composite Kernel-Based Elastic Net Classifier (CK-ENC)
3. Experimental Results
3.1. Experimental Datasets Description and Objective Metrics
3.1.1. Flevoland Benchmark Dataset
3.1.2. Yihechang Dataset
3.1.3. San Francisco Dataset
3.2. Comparison Algorithms and Experimental Setup
3.2.1. Impact of the Number of Superpixels
3.2.2. Impact of the Regularization Parameters
3.3. Classification Results Comparison
3.3.1. Experiment on Flevoland Dataset
3.3.2. Experiment on Yihechang Dataset
3.3.3. Experiment on San Francisco Dataset
4. Discussion
4.1. Impact of the Kernel Parameter
4.2. Impact of the Proposed Composite Kernel
4.3. Effect of the Number of Training Samples
4.4. Efficiency Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basic to Application; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hänsch, R.; Hellwich, O. Skipping the real world: Classification of PolSAR images without explicit feature extraction. ISPRS J. Photogramm. Remote Sens. 2018, 140, 122–132. [Google Scholar] [CrossRef]
- Xiang, D.; Tao, T.; Ban, Y.; Yi, S. Man-made target detection from polarimetric SAR data via nonstationarity and asymmetry. IEEE J. Sel. Topics. Appl. Earth Observ. Remote Sens. 2016, 9, 1459–1469. [Google Scholar] [CrossRef]
- Akbari, V.; Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T.; Moser, G.; Serpico, S.B. Polarimetric SAR change detection with the complex Hotelling–Lawley trace statistic. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3953–3966. [Google Scholar] [CrossRef] [Green Version]
- Biondi, F. Multi-chromatic analysis polarimetric interferometric synthetic aperture radar (MCAPolInSAR) for urban classification. Int. J. Remote Sens. 2019, 40, 3721–3750. [Google Scholar] [CrossRef]
- Lardeux, C.; Frison, P.L.; Tison, C.C.; Souyris, J.C.; Stoll, B.; Fruneau, B.; Rudant, J.P. Support vector machine for multifrequency SAR polarimetric data classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4143–4152. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Zhang, P.; Wu, Y.; Tan, X.; An, L. Mixture WGΓ-MRF model for PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 905–920. [Google Scholar] [CrossRef]
- Du, P.J.; Samat, A.; Waske, B.; Liu, S.C.; Li, Z.H. Random forest and rotation forest for fully polarized SAR image classification using polarimetric and spatial features. ISPRS J. Photogramm. Remote Sens. 2015, 105, 38–53. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR image classification using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Chen, Y.; Jiao, L.; Li, Y.; Zhao, J. Multilayer projective dictionary pair learning and sparse autoencoder for PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6683–6694. [Google Scholar] [CrossRef]
- Hu, Y.; Fan, J.; Wang, J. Classification of PolSAR images based on adaptive nonlocal stacked sparse autoencoder. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1050–1054. [Google Scholar] [CrossRef]
- Wen, Z.; Wu, Q.; Liu, Z.; Pan, Q. Polar-spatial feature fusion learning with variational generative-discriminative network for PoLSAR classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8914–8927. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Arii, M.; van Zyl, J.J.; Kim, Y. Adaptive model-based decomposition of polarimetric SAR covariance matrices. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1104–1113. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-component model-based decomposition for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Pottier, E.; Ferro-Famil, L. Unsupervised terrain classification preserving polarimetric scattering characteristics. IEEE Trans. Geosci. Remote Sens. 2004, 42, 722–731. [Google Scholar]
- Clound, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar]
- Clound, S.R.; Pottier, E. Integrating color features in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2197–2216. [Google Scholar]
- He, C.; Li, S.; Liao, Z.; Liao, M. Texture Classification of PolSAR Data Based on Sparse Coding of Wavelet Polarization Textons. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4576–4590. [Google Scholar] [CrossRef]
- Kim, H.; Hirose, A. Polarization feature extraction using quaternion neural networks for flexible unsupervised PolSAR land classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 2378–2381. [Google Scholar]
- Dong, H.; Xu, X.; Sui, H.; Xu, F.; Liu, J. Copula-based joint statistical model for polarimetric features and its application in PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5777–5789. [Google Scholar] [CrossRef]
- He, C.; He, B.; Tu, M.; Wang, Y.; Qu, T.; Wang, D.; Liao, M. Fully Convolutional Networks and a Manifold Graph Embedding-Based Algorithm for PolSAR Image Classification. Remote Sens. 2020, 12, 1467. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on the complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Lang, R.H.; Ranson, K.J. K-Distribution for Multi-Look Processed Polarimetric SAR Imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Pasadena, PA, USA, 8–12 August 1994; pp. 2179–2181. [Google Scholar]
- Freitas, C.C.; Frery, A.C.; Correia, A.H. The polarimetric G distribution for SAR data analysis. Environmetrics 2005, 16, 13–31. [Google Scholar] [CrossRef]
- Chi, L.; Liao, W.; Li, H.C.; Fu, K.; Philips, W. Unsupervised classification of multilook polarimetric SAR data using spatially variant wishart mixture model with double constraints. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5600–5613. [Google Scholar]
- Yang, F.; Gao, W.; Xu, B.; Yang, J. Multi-frequency polarimetric SAR classification based on Riemannian manifold and simultaneous sparse representation. Remote Sens. 2015, 7, 8469–8488. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Yang, W.; Song, H.; Huang, P. Polarimetric SAR image classification using geodesic distances and composite kernels. IEEE J. Sel. Topics. Appl. Earth Observ. Remote Sens. 2018, 11, 1606–1614. [Google Scholar] [CrossRef]
- Hänsch, R. Complex-Valued Multi-Layer Perceptrons—An Application to Polarimetric SAR Data. Photogramm. Eng. Remote Sens. 2010, 76, 1081–1088. [Google Scholar] [CrossRef]
- Kinugawa, K.; Shang, F.; Usami, N.; Hirose, A. Isotropization of Quaternion-Neural-Network-Based PolSAR Adaptive Land Classification in Poincare-Sphere Parameter Space. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1234–1238. [Google Scholar] [CrossRef]
- Shang, F.; Hirose, A. Quaternion neural-network-based PolSAR land classification in Poincare- sphereparameter space. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5693–5703. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric sar image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Y.; Zhang, P.; Liang, W.; Li, M. Pixel-wise PolSAR image classification via a novel complex-valued deep fully convolutional network. Remote Sens. 2019, 11, 2653. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Li, M.; Zhang, P.; Wu, Y.; Song, W. Complex-valued 3-D convolutional neural network for PolSAR image classification. IEEE Geosci. Remote Sens. Lett. 2019, in press. [Google Scholar] [CrossRef]
- Liu, W.; Yang, J.; Li, P.; Han, Y.; Zhao, J.; Shi, H. A novel object-based supervised classification method with active learning and random forest for PolSAR imagery. Remote Sens. 2018, 10, 1092. [Google Scholar] [CrossRef] [Green Version]
- Zhong, N.; Yang, W.; Cherian, A.; Yang, X.; Xia, G.; Liao, M. Unsupervised classification of polarimetric SAR images via Riemannian sparse coding. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5381–5390. [Google Scholar] [CrossRef]
- Liu, B.; Hu, H.; Wang, H.; Wang, K.; Liu, X.; Yu, X. Superpixel-based classification with an adaptive number of classes for polarimetric SAR images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 907–924. [Google Scholar] [CrossRef]
- Qin, F.; Guo, J.; Lang, F. Superpixel segmentation for polarimetric SAR imagery using local iterative clustering. IEEE Geosci. Remote Sens. Lett. 2015, 12, 13–17. [Google Scholar]
- Wu, Y.; Ji, K.; Yu, W.; Su, Y. Region-based classification of polarimetric SAR images using Wishart MRF. IEEE Geosci. Remote Sens. Lett. 2008, 5, 668–672. [Google Scholar] [CrossRef]
- Yang, R.; Hu, Z.; Liu, Y.; Xu, Z. A Novel Polarimetric SAR Classification Method Integrating Pixel-Based and Patch-Based Classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 431–435. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tupin, F.; Reigber, A.; Jäger, M. NL-SAR: A unified nonlocal framework for resolution-preserving (Pol)(In)SAR denoising. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2021–2038. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Jiao, L.; Wang, S.; Hou, B.; Liu, F. Adaptive nonlocal spatial–spectral kernel for hyperspectral imagery classification. IEEE J. Sel. Topics. Appl. Earth Observ. Remote Sens. 2016, 9, 4086–4101. [Google Scholar] [CrossRef]
- Jia, L.; Li, M.; Wu, Y.; Zhang, P.; Liu, G.; Chen, H.; An, L. SAR image change detection based on iterative label information composite kernel supervised by anisotropic texture. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3960–3973. [Google Scholar] [CrossRef]
- Tuia, D.; Ratle, F.; Pozdnoukhov, A.; Camps-Valls, G. Multisource composite kernels for urban-image classification. IEEE Geosci. Remote Sens. Lett. 2010, 7, 88–92. [Google Scholar] [CrossRef] [Green Version]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Du, Q.; Zhang, F.; Hu, W. Hyperspectral image classification by fusing collaborative and sparse representations. IEEE J. Sel. Topics. Appl. Earth Observ. Remote Sens. 2016, 9, 4178–4187. [Google Scholar] [CrossRef]
- Cao, F.; Hong, W.; Wu, Y.; Pottier, E. An unsupervised segmentation with an adaptive number of clusters using the SPAN/H/α/A space and the complex Wishart clustering for fully polarimetric SAR data analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3454–3467. [Google Scholar] [CrossRef]
- Arsigny, V.; Fillard, P.; Pennec, X.; Ayache, N. Log-euclidean metrics for fast and simple calculus on diffusion tensors. Mag. Resonance Med. 2006, 56, 411–4216. [Google Scholar] [CrossRef]
- Sra, S. Positive definite matrices and the S-divergence. Proc. Amer. Math. Soc. 2016, 144, 2787–2797. [Google Scholar] [CrossRef] [Green Version]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Feng, J.; Cao, Z.; Pi, Y. Polarimetric contextual classification of PolSAR images using sparse representation and superpixels. Remote Sens. 2014, 6, 7158–7181. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Wang, H.; Fan, J.; Ma, X.; Wang, B. Wishart distance-based joint collaborative representation for polarimetric SAR image classification. IET Radar Sonar Navigat. 2017, 11, 1620–1628. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2. [Google Scholar] [CrossRef]
















| Dataset | LMK-ENC | NWWK-ENC |
|---|---|---|
| Flevoland | 19 | 11 |
| Yihechang | 15 | 11 |
| San Francisco | 21 | 17 |
| Class | S-WML | RMRF | S-RF | CK-SVM | MDPL-SAE | ANSSAE | SRC-MV | JSRC-SP | W-JCRC | DK-SRC | CK-SRC | CK-CRC | CK-ENC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.28 ± 0.06 | 99.59 ± 0.07 | 99.39 ± 0.03 | 99.62 ± 0.11 | 95.74 ± 0.26 | 94.49 ± 0.56 | 99.69 ± 0.11 | 99.69 ± 0.17 | 99.47 ± 0.08 | 99.15 ± 0.25 | 99.74 ± 0.02 | 96.00 ± 0.78 | 99.47 ± 0.01 |
| 2 | 89.81 ± 1.71 | 99.64 ± 0.11 | 98.92 ± 0.19 | 99.68 ± 0.19 | 94.23 ± 0.80 | 93.47 ± 0.86 | 99.69 ± 0.02 | 99.69 ± 0.01 | 99.08 ± 0.20 | 99.43 ± 0.28 | 99.68 ± 0.01 | 99.90 ± 0.16 | 99.67 ± 0.03 |
| 3 | 94.93 ± 1.46 | 93.49 ± 1.01 | 98.55 ± 0.65 | 98.14 ± 0.29 | 95.68 ± 1.07 | 90.44 ± 0.51 | 97.94 ± 0.38 | 98.10 ± 0.27 | 96.62 ± 0.71 | 99.23 ± 0.30 | 99.06 ± 0.58 | 97.79 ± 0.45 | 99.18 ± 0.54 |
| 4 | 92.64 ± 0.66 | 98.86 ± 1.30 | 96.45 ± 1.06 | 99.86 ± 0.02 | 89.51 ± 1.55 | 93.66 ± 1.26 | 96.73 ± 1.78 | 99.57 ± 0.15 | 99.23 ± 0.30 | 97.83 ± 0.57 | 96.95 ± 0.79 | 97.99 ± 0.73 | 99.08 ± 0.02 |
| 5 | 86.24 ± 1.12 | 88.07 ± 1.20 | 83.98 ± 1.98 | 85.45 ± 1.39 | 97.41 ± 0.29 | 88.18 ± 0.50 | 96.66 ± 1.28 | 94.06 ± 0.94 | 92.68 ± 1.58 | 95.04 ± 0.55 | 97.32 ± 0.62 | 94.29 ± 1.58 | 98.11 ± 0.16 |
| 6 | 95.60 ± 0.21 | 97.79 ± 1.25 | 99.49 ± 0.28 | 99.41 ± 0.05 | 92.21 ± 0.57 | 70.79 ± 1.24 | 96.92 ± 0.53 | 94.10 ± 0.40 | 98.81 ± 0.71 | 97.62 ± 0.21 | 98.60 ± 0.18 | 98.75 ± 0.19 | 98.98 ± 0.01 |
| 7 | 98.27 ± 0.81 | 96.95 ± 0.95 | 98.20 ± 0.50 | 99.27 ± 0.07 | 87.42 ± 0.84 | 85.29 ± 1.01 | 93.69 ± 1.49 | 91.66 ± 0.55 | 95.25 ± 0.21 | 98.74 ± 0.47 | 99.46 ± 0.24 | 99.41 ± 0.36 | 99.18 ± 0.14 |
| 8 | 97.78 ± 1.28 | 94.98 ± 0.54 | 100 ± 0 | 100 ± 0 | 99.38 ± 0.48 | 98.86 ± 0.13 | 100 ± 0 | 100 ± 0 | 99.87 ± 0.06 | 99.22 ± 0.05 | 97.97 ± 0.17 | 97.98 ± 1.16 | 99.80 ± 0.01 |
| 9 | 87.99 ± 1.94 | 74.87 ± 1.66 | 95.26 ± 0.52 | 74.75 ± 2.46 | 90.91 ± 0.63 | 82.66 ± 0.37 | 99.86 ± 0.05 | 99.86 ± 0.26 | 92.75 ± 0.88 | 92.70 ± 1.43 | 96.53 ± 0.44 | 95.13 ± 1.45 | 96.14 ± 0.15 |
| 10 | 84.34 ± 0.42 | 78.24 ± 0.56 | 90.30 ± 0.18 | 64.30 ± 2.49 | 74.67 ± 2.22 | 65.20 ± 1.65 | 76.10 ± 2.16 | 70.96 ± 1.48 | 85.14 ± 1.67 | 93.67 ± 0.94 | 92.75 ± 0.60 | 89.86 ± 1.29 | 93.91 ± 0.22 |
| 11 | 91.91 ± 0.59 | 99.23 ± 0.03 | 97.51 ± 0.48 | 99.66 ± 0.03 | 92.10 ± 0.18 | 95.56 ± 1.16 | 99.15 ± 0.49 | 99.15 ± 0.43 | 94.91 ± 0.79 | 95.20 ± 0.91 | 99.08 ± 0.06 | 97.05 ± 1.91 | 98.88 ± 0.36 |
| 12 | 95.95 ± 0.41 | 97.89 ± 1.10 | 91.62 ± 0.92 | 84.77 ± 1.45 | 50.91 ± 1.78 | 80.36 ± 0.93 | 97.64 ± 0.99 | 97.64 ± 0.08 | 95.56 ± 1.05 | 98.97 ± 0.24 | 98.98 ± 0.46 | 96.13 ± 0.51 | 95.18 ± 1.10 |
| 13 | 94.51 ± 0.96 | 95.61 ± 0.97 | 91.48 ± 1.12 | 92.51 ± 0.74 | 94.99 ± 0.45 | 94.43 ± 0.45 | 99.32 ± 0.22 | 98.06 ± 0.30 | 98.23 ± 1.05 | 99.02 ± 0.03 | 98.31 ± 0.67 | 97.33 ± 1.21 | 99.01 ± 0.68 |
| 14 | 69.27 ± 1.14 | 49.41 ± 1.27 | 91.23 ± 0.07 | 50.81 ± 2.64 | 81.97 ± 1.83 | 88.62 ± 0.46 | 100 ± 0 | 100 ± 0 | 99.11 ± 0.43 | 99.93 ± 0.02 | 99.55 ± 0.31 | 97.79 ± 1.24 | 98.34 ± 0.86 |
| 15 | 98.71 ± 0.12 | 92.70 ± 0.87 | 99.16 ± 0.45 | 98.42 ± 0.02 | 94.54 ± 0.32 | 97.90 ± 0.26 | 99.12 ± 0.12 | 99.12 ± 0.12 | 96.71 ± 0.32 | 98.93 ± 0.58 | 81.36 ± 1.45 | 98.93 ± 0.18 | 98.46 ± 0.04 |
| OA | 90.65 ± 0.85 | 89.54 ± 0.29 | 94.04 ± 0.10 | 87.83 ± 0.36 | 88.13 ± 0.89 | 86.74 ± 0.59 | 96.21 ± 0.65 | 95.11 ± 0.54 | 95.94 ± 0.33 | 97.66 ± 0.32 | 98.06 ± 0.05 | 97.05 ± 0.27 | 98.18 ± 0.09 |
| AA | 91.75 ± 0.54 | 90.49 ± 0.25 | 93.50 ± 0.03 | 89.65 ± 0.35 | 88.78 ± 1.17 | 87.99 ± 0.52 | 96.83 ± 0.12 | 96.11 ± 0.43 | 96.29 ± 0.25 | 96.64 ± 0.39 | 97.02 ± 0.64 | 97.20 ± 0.84 | 98.23 ± 0.17 |
| 100 | 89.91 ± 0.92 | 88.62 ± 0.32 | 95.31 ± 0.11 | 86.76 ± 0.39 | 87.05 ± 0.96 | 85.55 ± 0.64 | 95.86 ± 0.71 | 94.66 ± 0.60 | 95.56 ± 0.35 | 97.45 ± 0.35 | 97.89 ± 0.39 | 96.79 ± 0.30 | 98.01 ± 0.01 |
| Class | S-WML | RMRF | S-RF | CK-SVM | MDPL-SAE | ANSSAE | SRC-MV | JSRC-SP | W-JCRC | DK-SRC | CK-SRC | CK-CRC | CK-ENC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 92.86 ± 0.78 | 91.04 ± 0.21 | 97.04 ± 0.41 | 96.44 ± 0.74 | 98.04 ± 0.79 | 97.03 ± 0.43 | 91.61 ± 0.79 | 92.12 ± 0.87 | 79.45 ± 2.12 | 89.03 ± 1.60 | 95.00 ± 0.25 | 91.90 ± 1.29 | 92.64 ± 0.75 |
| 2 | 71.62 ± 1.59 | 78.60 ± 2.63 | 96.47 ± 0.25 | 79.17 ± 2.41 | 81.79 ± 1.09 | 72.18 ± 1.62 | 89.68 ± 1.24 | 92.70 ± 0.27 | 87.25 ± 1.78 | 92.11 ± 0.70 | 89.67 ± 0.80 | 91.31 ± 0.56 | 92.82 ± 0.56 |
| 3 | 80.75 ± 1.08 | 81.41 ± 1.53 | 84.57 ± 1.99 | 65.53 ± 2.15 | 48.28 ± 3.57 | 69.78 ± 2.70 | 84.65 ± 1.75 | 90.50 ± 1.75 | 91.27 ± 0.80 | 87.09 ± 1.63 | 90.66 ± 1.35 | 93.60 ± 1.28 | 92.44 ± 1.19 |
| 4 | 96.02 ± 0.95 | 96.17 ± 0.49 | 90.89 ± 0.27 | 80.51 ± 1.23 | 88.11 ± 0.76 | 82.61 ± 1.37 | 94.97 ± 0.18 | 89.85 ± 1.94 | 94.84 ± 0.27 | 96.31 ± 0.47 | 97.83 ± 0.73 | 97.22 ± 0.59 | 98.48 ± 0.63 |
| OA | 90.91 ± 1.07 | 91.64 ± 0.54 | 91.33 ± 0.39 | 80.14 ± 0.88 | 83.07 ± 0.98 | 81.38 ± 1.20 | 92.58 ± 0.36 | 90.51 ± 1.17 | 91.75 ± 0.97 | 93.74 ± 0.76 | 95.63 ± 0.26 | 95.47 ± 0.26 | 96.36 ± 0.22 |
| AA | 85.31 ± 1.28 | 86.81 ± 1.17 | 92.24 ± 0.26 | 80.41 ± 0.91 | 79.06 ± 1.22 | 80.40 ± 0.28 | 90.23 ± 0.43 | 91.29 ± 0.94 | 88.20 ± 1.74 | 91.14 ± 0.57 | 93.29 ± 0.27 | 93.51 ± 0.17 | 94.10 ± 0.44 |
| 100 | 83.20 ± 1.42 | 84.48 ± 0.88 | 84.93 ± 0.58 | 66.90 ± 0.89 | 70.60 ± 1.71 | 68.38 ± 1.69 | 86.59 ± 0.69 | 85.53 ± 1.85 | 85.08 ± 1.74 | 88.64 ± 1.31 | 92.02 ± 0.44 | 91.77 ± 0.46 | 93.34 ± 0.38 |
| Class | S-WML | RMRF | S-RF | CK-SVM | MDPL-SAE | ANSSAE | SRC-MV | JSRC-SP | W-JCRC | DK-SRC | CK-SRC | CK-CRC | CK-ENC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.11 ± 0.85 | 99.15 ± 0.23 | 99.03 ± 0.04 | 100 ± 0 | 95.61 ± 0.76 | 99.69 ± 0.24 | 99.99 ± 0.01 | 99.96 ± 0.02 | 99.91 ± 0.05 | 99.96 ± 0.04 | 99.98 ± 0.08 | 99.47 ± 0.27 | 99.95 ± 0.01 |
| 2 | 90.88 ± 1.16 | 88.62 ± 1.09 | 94.83 ± 1.13 | 93.75 ± 0.88 | 84.80 ± 1.47 | 86.41 ± 1.54 | 92.80 ± 0.53 | 90.85 ± 0.98 | 82.87 ± 1.70 | 90.87 ± 1.42 | 92.85 ± 1.47 | 89.26 ± 1.15 | 92.03 ± 0.98 |
| 3 | 65.20 ± 2.94 | 83.92 ± 1.89 | 79.23 ± 2.07 | 43.69 ± 2.10 | 77.92 ± 0.09 | 76.25 ± 0.93 | 74.76 ± 1.94 | 89.67 ± 1.43 | 90.07 ± 0.46 | 93.08 ± 0.63 | 98.13 ± 0.48 | 92.74 ± 1.47 | 97.27 ± 0.64 |
| 4 | 92.20 ± 1.05 | 73.84 ± 2.27 | 84.25 ± 1.67 | 72.06 ± 0.94 | 83.29 ± 2.42 | 58.91 ± 0.91 | 96.73 ± 1.14 | 96.03 ± 1.16 | 78.56 ± 1.87 | 77.40 ± 2.16 | 92.79 ± 1.59 | 97.05 ± 1.48 | 96.16 ± 0.02 |
| 5 | 80.05 ± 1.75 | 69.78 ± 0.67 | 92.33 ± 0.40 | 58.97 ± 1.31 | 79.56 ± 0.22 | 74.24 ± 1.15 | 73.66 ± 1.54 | 84.25 ± 1.80 | 89.60 ± 0.74 | 83.33 ± 1.59 | 92.76 ± 1.50 | 95.54 ± 0.72 | 96.41 ± 0.47 |
| OA | 90.04 ± 1.28 | 89.14 ± 0.92 | 92.20 ± 0.39 | 83.07 ± 0.44 | 88.30 ± 1.42 | 85.19 ± 1.32 | 93.27 ± 0.10 | 95.68 ± 0.48 | 91.51 ± 1.10 | 92.55 ± 1.11 | 97.03 ± 0.33 | 96.43 ± 0.49 | 97.59 ± 0.24 |
| AA | 85.29 ± 1.81 | 83.06 ± 1.11 | 89.93 ± 1.19 | 73.69 ± 0.56 | 84.23 ± 0.40 | 79.10 ± 2.15 | 87.59 ± 1.56 | 92.15 ± 1.63 | 88.20 ± 1.00 | 88.93 ± 1.48 | 95.30 ± 0.51 | 94.82 ± 0.21 | 96.36 ± 0.40 |
| 100 | 85.69 ± 0.81 | 84.41 ± 1.33 | 88.80 ± 0.34 | 75.57 ± 0.60 | 83.16 ± 0.53 | 78.30 ± 0.83 | 90.28 ± 0.30 | 93.78 ± 0.21 | 87.83 ± 1.55 | 89.30 ± 0.59 | 95.73 ± 0.47 | 94.87 ± 0.70 | 96.54 ± 0.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Wu, Y.; Li, M.; Liang, W.; Zhang, P. PolSAR Image Classification Using a Superpixel-Based Composite Kernel and Elastic Net. Remote Sens. 2021, 13, 380. https://doi.org/10.3390/rs13030380
Cao Y, Wu Y, Li M, Liang W, Zhang P. PolSAR Image Classification Using a Superpixel-Based Composite Kernel and Elastic Net. Remote Sensing. 2021; 13(3):380. https://doi.org/10.3390/rs13030380
Chicago/Turabian StyleCao, Yice, Yan Wu, Ming Li, Wenkai Liang, and Peng Zhang. 2021. "PolSAR Image Classification Using a Superpixel-Based Composite Kernel and Elastic Net" Remote Sensing 13, no. 3: 380. https://doi.org/10.3390/rs13030380
APA StyleCao, Y., Wu, Y., Li, M., Liang, W., & Zhang, P. (2021). PolSAR Image Classification Using a Superpixel-Based Composite Kernel and Elastic Net. Remote Sensing, 13(3), 380. https://doi.org/10.3390/rs13030380