Next Article in Journal
The Impact of Assimilating Satellite Radiance Observations in the Copernicus European Regional Reanalysis (CERRA)
Next Article in Special Issue
Research on Temporal and Spatial Resolution and the Driving Forces of Ecological Environment Quality in Coal Mining Areas Considering Topographic Correction
Previous Article in Journal
Inversion of Terrain Slope and Roughness with Satellite Laser Altimeter Full-Waveform Data Assisted by Shuttle Radar Topographic Mission
Previous Article in Special Issue
NDVI as a Proxy for Estimating Sedimentation and Vegetation Spread in Artificial Lakes—Monitoring of Spatial and Temporal Changes by Using Satellite Images Overarching Three Decades
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 3
10.3390/rs13030425
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors

by
Zhongming Guo
1,2,
Lei Geng
3,
Baoshou Shen
1,2,*,
Yuwei Wu
1,2,
Anan Chen
1,2 and
Ninglian Wang
1,2
1
Shaanxi Key Laboratory of Earth Surface System and Environmental Carrying Capacity, Xi’an 710127, China
2
Institute of Earth Surface System and Hazards, College of Urban and Environmental Sciences, Northwest University, Xi’an 710127, China
3
School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(3), 425; https://doi.org/10.3390/rs13030425
Submission received: 15 December 2020 / Revised: 20 January 2021 / Accepted: 22 January 2021 / Published: 26 January 2021
(This article belongs to the Special Issue Advances of Remote Sensing in the Analysis of the Spatial and Temporal Variability of Land Surface)
Browse Figures
Versions Notes

Abstract

:
The glacier snowline altitude (SLA) at the end of the melt season is an indicator of the glacier equilibrium line altitude and can be used to estimate glacier mass balance and reconstruct past climate. This study analyzes the spatiotemporal variability in glacier SLA across High Mountain Asia, including the Altai Mountains, Karakoram Mountains, Western Himalayas, Gongga Mountains, Tian Shan, and Nyainqentanglha Mountains, over the past 30 years (1989–2019) to better elucidate the state of these mountain glaciers. Remote-sensing data are processed to delineate the glacier SLA across these mountainous regions, and nearby weather station data are incorporated to determine the potential relationships between SLA and temperature/precipitation. The mean SLAs across the Altai and Karakoram mountains ranged from 2860 ± 169 m to 3200 ± 152 m and from 5120 ± 159 m to 5320 ± 240 m, respectively, with both regions experiencing an average increase of up to 137 m over the past 30 years. Furthermore, the mean glacier SLAs across the Western Himalayas and Gongga Mountains increased by 190–282 m over the past 30 years, with both regions experiencing large fluctuations. In particular, the mean glacier SLA across the Western Himalayas varied from 4910 ± 190 m in 1989 to 5380 ± 164 m in 2000, and that across the Gongga Mountains varied from 4960 ± 70 m in 1989 to 5330 ± 100 m in 2012. Correlation analyses between glacier SLA and temperature/precipitation suggest that temperature is the primary factor influencing glacier SLA across these High Mountain Asia glaciers. There is a broad increase in glacier SLA from the Altai Mountains to the Karakoram Mountains, with a decrease in glacier SLA with decreasing latitude across the Himalayas; the maximum SLA occurs near the northern slopes of the Western Himalayas. The glacier SLA is lower on the eastern side of the Tibetan Plateau and exhibits a longitudinal distribution pattern. These results are expected to provide useful information for evaluating the state of High Mountain Asia glaciers, as well as their response and feedback to climate change.

Graphical Abstract

1. Introduction

Mountain glacier is a critical component of the Earth’s system, and its serve as a key freshwater source in many regions [1]. Glacier changes also have a significant impact on sea level [2]. Moreover, they can also lead to devastating natural disasters, including outburst glacier floods and glacier debris flow [3]. Changes in mountain glaciers also serve as a primary indicator of climate change. Glacier variation can be determined by monitoring changes in glacier area, length, mass balance, equilibrium line altitude (ELA, the ELA is a line on the glacier where annual accumulation equals ablation) or snowline altitude (SLA), and the contribution of global mountain glaciers and small ice caps to sea-level rise can be estimated through mass balance calculation [4]. Observations of glacier/snow parameters (e.g., mass balance and ELA) from a large mountain range and/or cryospheric region can assist to identify the influence of meteorological parameters (e.g., temperature and precipitation) on glacier changes for a region of interest, and promote better understanding of the relationship between glaciers and the climate at a regional scale. In particular, the ELA of glaciers can be used to determine the transient accumulation area ratio (AAR) and further estimate the mass balance of glaciers [5,6,7]. However, mass balance monitoring in general requires substantial financial and technical support to conduct ground-based observations, and thus it is difficult obtain mass balance data covering a large regions due to the limited number of ground observation sites. Paterson [8] indicated that the SLA at the end of the melt season is approximately equal to the ELA. Therefore, SLA has been used to represent ELA in mid-latitude glaciers [6,9,10,11].
Remote sensing is a powerful tool to monitor the evolution of glacial systems, due to its high temporal-spatial resolution and coverage, and is particularly useful to map SLA of glaciers where ground-based observations and/or regional-scale constraints are rare [12]. To discern SLA from remote sensing data, analysts first need to extract the snow boundary or area [13,14], then distinguish the boundary between snow and ice, and finally, a digital elevation model (DEM) is used to determine SLA [15,16]. This SLA recognition procedure utilizes different data processing methods, including the band combination method [17,18], the band ratio method [9,13] and the threshold method [19,20]. Extant literatures have also used MODIS data to determine regional SLA in the Tibetan Plateau and its environs [21,22,23,24]. However, the research results on glacial changes in High Mountain Asia so far are still quite scarce. In particular, High Mountain Asia glaciers are critical for both the global water cycle and water eco-environment in the arid regions of central Asia. Therefore, in this paper, the quantitative method based on the difference between snow and ice albedo determines a single glacier SLA.
In this study, we present remote sensing data covering High Mountain Asia, where the SLA of different glaciers and there changes over the past ~20 years are identified. The resultant SLA data are then compared with local meteorological data including summer mean temperature and precipitation, in order to explore the potential influence of weather and/or climate conditions on SLA changes. The results are expected to provide information that is useful to evaluate the state of High Mountain Asia glaciers and their response and feedback to climate change.

2. Study Site

High Mountain Asia (27–50°N, 70–105°E) comprises the Tibetan Plateau and surrounding Asian mountain ranges and possesses the largest cryosphere environment outside of the Polar Regions (Figure 1). They are bounded by the Altai Mountains to the north, the Himalayas to the south, the Pamir Mountains and the Western Tian Shan to the west, and the Qilian Mountains and the Hengduan Mountains to the east. There are 97,974 modern glaciers across this region, covering a vast area of 98,768.86 km2 with ice storage of 1.1 × 104 to 1.5 × 104 km3, and producing 110–150 km3 melt water annually [25].
The western and northern regions of High Mountain Asia are affected primarily by the westerlies, whereas the southwest region is affected mainly by the Indian monsoon. The eastern and southeastern regions are influenced mainly by the East Asian monsoon and also by the plateau monsoon caused by the uplift of the Tibetan Plateau [26,27]. Owing to the impact of different wind systems, High Mountain Asia regional glaciers can be catalogued as continental or marine glaciers in the southwest and continental or polar glaciers in the northwest [26,28]. Annual precipitation ranges from 600 to 1000 mm in the Altai Mountains to above 3000 mm in the southeast region of High Mountain Asia. Precipitation is the material basis of mass balance and ELA changes. Accordingly, glacier ELAs vary from 2800 m in the Altai Mountains to 6200 m in the Himalayas [29].
Temporal variations in SLA were investigated by selecting subsets of representative glaciers in both the monsoon and westerlies regions of High Mountain Asia. Glaciers from the Altai Mountains (6) and the Karakoram Mountains (9) were chosen to represent the westerlies region, and glaciers from the Western Himalayas (12) and the Gongga Mountains (5) were chosen to represent the monsoon region. The locations of the selected glaciers are listed in Figure 1.

3. Data and Methods

3.1. Data

Landsat Multispectral Scanner System (MSS)/Thematic Mapper ™/Enhanced Thematic Mapper Plus (ETM+)/Operational Land Imager (OLI) data were downloaded from the USGS (http://earthexplorer.usgs.gov/) and the Geospatial Data Cloud (http://www.gscloud.cn). According to the three criteria for image selection, Landsat images of the Altai Mountains, the Karakoram Mountains, the Himalayas, and the Gongga Mountain from 1989 to 2019 were screened (Table 1).
Landsat data have a high spatial resolution (30 m) and long time series, making them an ideal remote-sensing dataset for mapping glacier SLA. High Mountain Asia glaciers have a long melt season (generally the June–August timeframe), such that the highest SLA may occur on any day in either July or August (occasionally in early September). However, the data used in this study may not capture the highest SLA due to the large number of sensors and relatively low temporal resolution (8–16 days) of the Landsat satellites, which introduces a degree of uncertainty in the extracted SLA. Here we limit our data range for determining the glacier SLA to remote-sensing images that were acquired between 7 July and 15 September during the 1989–2019 period. Approximately 75% of the Landsat scenes that were analyzed for glacier SLA extraction were acquired in August (Figure 2).
Sentinel-2 data were used to evaluate the uncertainty in the Landsat-derived glacier SLA that arose from inconsistent Landsat data acquisition times since Sentinel-2 images possess a considerably higher spatiotemporal resolution. Sentinel 2A and 2B were launched in June 2015 and March 2017, respectively. Both satellites have a maximum spatial resolution of 10 m, and a temporal resolution to 5 days is achieved when Sentinel 2A and 2B data are analyzed together. We selected Sentinel-2 data that spanned the May 1–October 31, 2018 period for our analysis. Furthermore, the temporal proximity of the Sentinel-2 data to the Landsat data provides the opportunity to construct a long-term time series of glacier SLA from these two datasets.
Moderate Resolution Imaging Spectroradiometer (MODIS) data, which possess a high temporal resolution, were used to interpolate the glacier SLA where it was not extracted from the Landsat scenes. We preprocessed the MOD10A data to extract the glacier SLA [30], and then used Landsat data as the “true values” to verify the MODIS-derived glacier SLA, and obtain the annual snowline positions. We used the Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) (http://earthexplorer.usgs.gov/) to determine the snowline position on each analyzed glacier; the horizontal and vertical accuracies of the DEM are ± 20   m and ± 16   m , respectively.
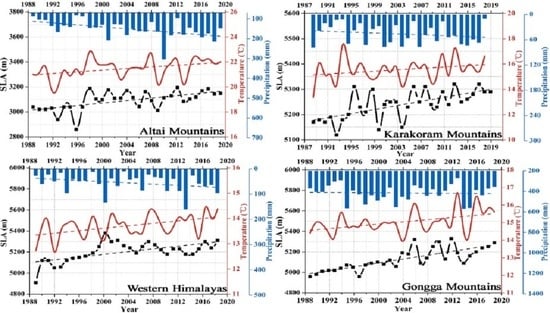
The meteorological data were obtained from the China Meteorological Data Service Center (http://data.cma.cn/) and NOAA National Climatic Data Center (NCDC) (http://www.ncdc.noaa.gov/).
There are two main functions of the meteorological data in this study. The first is to evaluate the Landsat-derived SLA uncertainty using Sentinel 2 data. Temperature and precipitation data were also acquired from Tuole weather station, which is near Qiyi Glacier in the Qilian Mountains. The second function is to discuss the effects of temperature and precipitation on glacier SLA across High Mountain Asia. We acquired data from the nearest meteorological stations to the analyzed glacier areas during the 1998–2019 period; detailed information on the nearest meteorological stations in our study area is provided in Table 2. The analyzed glacier regions, with the exception of the Altai Mountains, mainly experience summer accumulation and melt, such that the average summer (June–August) temperature and precipitation were mainly collected for the analysis. We acquired summer precipitation and cold season (September–May) precipitation for the Altai Mountains since this region mainly experiences summer melt and cold season accumulation.

3.2. Methods

Data processing methods included data screening, pre-processing and SLA determination. Data screening mainly followed three criteria or principles: Landsat TM/ETM+/LC 8 images with (1) little cloud cover, (2) no recent snowfall on the glaciers, and (3) at the end of the summer melt season (July–August) were preferentially selected to enhance the probability of extracting the highest snowline or minimum snow cover. Image pre-processing included radiometric calibration, registration, atmospheric correction, and narrow-band to broadband albedo conversion. The subsequent delineation of the SLA was based on the registered DEM.
Radiation calibration is the process of converting a digital number (DN) to a corresponding radiation. The radiation of Landsat Level 1 product was calculated using the following equation:
Lλ = ML × Qcal + AL
where Lλ is TOA spectral radiance [W (m−2·sr−1·μm−1)], ML is band-specific gain from the metadata; Qcal is quantized and calibrated standard product pixel values; and AL is band-specific bias from the metadata.
Image registration is the process of matching and superposing two or more images acquired at different times, by different sensors (imaging devices) or under different conditions (i.e., weather, illumination, camera position and angle). In this study, Landsat image (ID: LT514402619980826, mean cloud cover: 4.57%) was taken as the base image to calibrate other Landsat images. The registered Landsat data was used as a base image to register the DEM data. This study utilized the ENVI software’s automatic accurate registration function, which makes the root mean square error (RMSE) of the ground control points less than 1, and performs quadratic polynomial correction to ensure registration accuracy and eventually obtains images with high registration quality.
Atmospheric correction can been used to reduce or eliminate the effect of atmospheric water vapor on the sensor, and can further calculate the narrowband albedo of the image. The FLAASH (Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes) module based on Modtran 4+ radiation transfer code was adopted in this study. This model can quickly perform atmospheric corrections of multispectral, hyperspectral data and aerial images, which could effectively eliminate the influence of atmosphere and light on the reflection of objects. The equation can be written as:
L = A × ρ/(1 − ρe × S) + B × ρe/(1 − ρe × S) + La
where L is the surface radiance [W (m−2·sr−1·μm−1)]; ρ is the pixel surface reflectance; ρe is the mean surface reflectance of the pixel and its surrounding regions; S is the spherical albedo of the atmosphere; La is the backscattering radiation of the atmosphere; and A, B is the coefficient which is related to the atmospheric and geometric conditions, but not to the underlying surface.
Our study determined the boundary between snow and bare ice based on the difference of their albedo. However, the albedo has not been directly obtained from satellites observations. Signals received by satellite sensors originate from radiances constitute radiation from a particular direction in narrowband at the top of the atmosphere. These signals must be converted to surface albedo. Based on near-surface and aircraft measurements, Greuell [31] established a narrowband-to-broadband albedo conversion model for glacier ice and snow, and it has a residual standard deviation of 0.011 for Landsat images. The equation is as follows:
α = 0.539 × ρi + 0.166 × ρj × (1 + ρj)
where α is the albedo; ρ is the narrowband albedo; i and j represent the specific band. For Landsat MSS, i and j represent the 1st and 3rd bands, respectively. For Landsat TM/ETM+, I and j represent the 2nd and 4th bands, respectively, because Landsat OLI has been changed in the band setting (a band is added in the visible band), and i and j represent the 3rd and 5th bands, respectively.
In order to calculate broadband albedo, the downloaded level-1C Sentinel 2 data need to conduct atmospheric correction. We will convert top-of-atmosphere reflectance of Level 1C Sentinel 2 data to surface reflectance data using the Sen2cor software. Sen2cor can be found on http://step.esa.int/main/third-party-plugins-2/sen2cor/. The atmospherically corrected Sentinel 2 data (Level 2A) were resembled using SNAP software and then converted to ENVI format for output. A narrow-to-broadband conversion was then performed through ENVI software to obtain the broadband albedo [32,33]. Snow line locations were determined based on the difference of albedo between the ice and snow. The snow line locations were extracted in the same way as the Landat data. In this case, the broadband albedo is obtained by the following equation,
A = 0.356ρ2 + 0.130ρ4 + 0.373ρ8 + 0.085ρ11 + 0.072ρ12 − 0.0018
where α is the albedo; ρ is the narrowband albedo; 2, 4, 8, 11, and 12 represent the specific band of Sentinel 2.
Based on the registered DEM data, its contour layer was extracted and overlaid with the broadband albedo image, and then the glacier surface was classified according to the difference between snow and bare ice albedo by ArcGIS software. If there was no transition zone between snow and bare ice, the boundary between snow and bare ice was defined as a snowline; if a transition zone existed, the boundary between snow and the transition zone was defined as a snowline. The SLA was then determined by the DEM contour layer by linking the lower edges of snowlines. It is possible that a snowline crosses several contours and does not coincide with a contour; in this case, the mean contour near the snowline was considered as the SLA [15,19] (Figure 3).
There are fewer available Landsat scenes for assessing the glacier SLA uncertainty over different dates in a given period due to the temporal resolution of the Landsat images and the impacts of clouds and new snowfall. We therefore combined the Sentinel-2 data, which possess a high temporal resolution (five days when using the data from 2A and 2B). Similarly, the Landsat temporal resolution, cloud cover, fresh snowfall, and stripe of the Landsat ETM data, all of which may result in missing data, could affect the glacier SLA time series reconstruction and analysis of glacier SLA variability over time. In particular, the glacier SLA in a given single year may determine the linear trend of the entire SLA, making it critical to have a complete SLA time series. MODIS data have a high temporal resolution (1 day) and long time series (data acquisition since 2000), but they possess a low spatial resolution (≤500 m); we therefore used the Landsat-derived SLAs as the “true values” to correct the MODIS-derived SLAs and further interpolate the Landsat-derived SLA time series (Figure 4).

4. Results and Discussions

4.1. Glacier SLA Accuracy Evaluation

Glacier SLA can reflect glacier changes, and is therefore a sensitive indicator of climate changes; these changes can be inferred from the degree of SLA variability. Furthermore, we can also estimate the glacier equilibrium line altitude (ELA), as well as the glacier mass balance, water volume, and runoff based on the SLA, highlighting the need to ensure the accuracy of the extracted SLA data. The glacier SLA accuracy is primarily affected by the data source (temporal and spatial resolution of the satellite imagery, and length of the data time series, if temporal glacier SLA changes are investigated). Cloud cover (especially in the southeastern region of the Tibetan Plateau), fresh snowfall, Landsat ETM data strips, and different extraction methods will likely affect the data accuracy. Furthermore, the precision of the DEM also determines the SLA accuracy since the DEM must be analyzed to obtain the glacier SLA. The accuracy of the extracted glacier SLA can generally be improved if the spatial resolution of the image is high. However, each data type has its own advantages and disadvantages when analyzing spatiotemporal SLA variability, such that joint analysis of multiple remote-sensing datasets can be considered.
We primarily selected images from the mid/late July–early September timeframe because the glacier SLA at the end of the ablation period should be the maximum SLA for a given year, which means that this SLA can represent the ELA. This image selection process also allowed us to evaluate and reduce the impact of image spatial resolution on glacier SLA. The ablation period mainly occurs in the June–August timeframe, although the highest SLA may be observed in early September if either warmer temperatures persist or there is little/no new precipitation. Approximately 90% of the analyzed Landsat images were acquired in the late July–August timeframe, with 75% acquired in August and 15% acquired in late July (Figure 2).
Sentinel-2 images (1 May–31 October 2018 timeframe) were also used to further evaluate the influence of the temporal resolution of the sensor on glacier SLA (Figure 5). The relationship between glacier SLA and temperature/precipitation during the ablation season was analyzed using the Sentinel-2 images, and temperature and precipitation observations from Tuole weather station, which is near Qiyi Glacier (Figure 5). We extracted the glacier SLA from 15 images during the ablation season due to the influences of new snowfall, cloud cover, and the temporal resolution of the satellite images. The glacier SLA was above 4600 m from July 28 to September 6, with a maximum SLA of 4873 m observed on August 12. The results indicated that the average variability from the highest SLA (August 12) during the late July–August timeframe was 132 m, with minimum and maximum variations of 29 and 268 m, respectively. These Sentinel-2-derived glacier SLA data suggest that our analysis of the Landsat scenes that were mainly acquired in August to extract glacier SLA could extract the highest glacier SLA. A comparison and analysis of our extracted glacier SLA positions with temperature and precipitation data revealed that the extracted SLAs from the late July–early September timeframe were high due to higher temperatures and less precipitation during this period. The highest SLA does not appear around July 31, when the temperature is highest, because there is more precipitation at the end of July. The highest SLA, which was acquired on August 12, was due to relatively high temperatures and less precipitation in the middle of August. Our correlation coefficient statistics indicate that glacier SLA is positively correlated with temperature (r = 0.56), which suggests that glacier SLA is mainly influenced by temperature. Temperature, precipitation, and SLA all show downward linear trends, which also indicates that temperature is the main factor influencing the observed glacier SLA variations.
We set a cloud cover threshold during the image filtering process, and then manually selected the appropriate images to avoid the influence of cloud cover on glacier SLA extraction. However, this resulted in the inability to obtain the SLA across some glaciers in a given year, which we express as “NA” in Table 3. We also manually filtered the images with no fresh snowfall to avoid the effects of new snowfall. We note that there were stripes in the Landsat ETM data after 2003; these stripes were removed by applying nearest-neighbor interpolation to estimate the pixel values of the area covered by land. We extracted the snow line based on the albedo difference between the ice and snow, and set a threshold to segment the ice surface, with the boundary between the snow and ice marking the position of the snow line. The boundary between the snow and transition zone was treated as the location of the snow line if a transition zone was present. The albedo was obtained via our inversion approach, which is outlined in Section 3. Previous studies have shown that the absolute error between the albedo retrieved from Qiyi Glacier and the measured albedo is within 0.05 [34]. A DEM with a higher spatial resolution can be used to improve the accuracy of the glacier SLA; therefore, we used a SRTM DEM that possessed a 30 m spatial resolution and ~16 m linear vertical absolute height error to ensure the high accuracy of the extracted glacier SLAs.

4.2. Glacier SLA across the Altai Mountains

The glacier SLA across the Altai Mountains is presented in Table 3. We were unable to determine the SLA of some glaciers in a given year due to occasional cloud cover. The lowest and highest SLAs in the time series were 2600 m at A1 Glacier in 1996 and 3540 m at A8 Glacier in 2015, respectively, with 940 m of variability among the 12 analyzed glaciers. The SLA changes for the individual glaciers across Altai Mountains during the 1989–2019 period are shown in Figure 6. All of the glacier SLAs exhibit an upward trend. The SLA change of an individual glacier was in the 31–302 m range during the study period, with most of the analyzed glaciers exhibiting SLA changes in the 100–300 m range; A8 Glacier possessed the largest change (Figure 6a). Three glaciers (A3, A6, and A7) possessed a relatively stable SLAs, with an average increase of 42 m. The largest SLA variability during the study period was observed along A1 Glacier (SD = 156 m), whereas A3 Glacier possessed the smallest SLA variability (SD = 71 m; Figure 6b). The mean SLA of A8 Glacier was the highest among the analyzed glaciers across the Altai Mountains (3370 ± 142 m), and A6 Glacier possessed the lowest mean SLA at 2910 ± 92 m. The reason for the large SLA difference or variability among the 12 glaciers in a given year may be related to spatial differences in precipitation, temperature, and/or topography (such as aspect and slope).
The mean glacier SLA variability at the end of the melt season (generally August) across the Altai Mountains during the 1989–2019 period is shown in Figure 7. The mean glacier SLA generally increased over time, which indicates that the glaciers were in a state of ablation throughout the 1989–2019 period. The SLAs ranged from 2860 ± 169 m in 1996 to 3260 ± 152 m in 2012, with a maximum variability of 721 m. Furthermore, linear regression analysis revealed that the mean glacier SLA across the Altai Mountains declined by 151 m during the 1989–2019 period.
Meteorological data from the Haba River weather station were used to determine the effects of temperature and precipitation on glacier SLA across the Altai Mountains. The general temperature and precipitation trends should be similar in a relatively small region, such as the weather station and nearby glaciers, even though regional variations in the meteorological conditions exist. We calculated the total precipitation for the September–May timeframe and summer mean temperature for the June–August timeframe since these glaciers generally experienced accumulation during the cold season and strong ablation during the summer (Figure 7). The cold season precipitation and summer mean temperature both increased during our analysis period, suggesting that increased summer ablation might be the key reason for the increased SLA. The mean glacier SLA observations across the Altai Mountains generally exhibited a significant positive correlation with temperature (Figure 7). We calculated the correlation coefficients between mean SLA and summer mean temperature (r = 0.55; 95% confidence level) and cold season precipitation (r = 0.38), with the summer mean temperature being the primary factor influencing glacier SLA across the Altai Mountains. The linear trends in summer mean temperature and mean SLA further suggest that temperature exerts the primary influence on the glacier SLA changes across the Altai Mountains.

4.3. Glacier SLA across the Karakoram Mountains

The glacier SLA across the Karakoram Mountains is shown in Table 4. It varied by 950 m, ranging from 4710 m at K3 Glacier in 2010 to 5660 m at K8 Glacier in 2013. The individual mean glacier SLA changes ranged from 22 to 412 m during the study period (Figure 8a), with K1, K3, and K4 glaciers exhibiting slight SLA changes (<50 m increase), and K8 Glacier exhibiting a 412 m increase over the past 30 years. Four glacier SLAs exhibited increases of >100 m. K8 Glacier exhibited the largest SLA variability (SD = 164 m; Figure 8b), whereas K7 Glacier possessed a relatively stable SLA (SD = 46 m) during the 1989–2019 period. K5 Glacier possessed the highest mean SLA at 5510 ± 66 m, and K3 Glacier possessed the lowest mean SLA at 4970 ± 124 m.
The mean SLA across the Karakoram Mountains at the end of the melt season (generally August) during the 1989–2019 period is shown in Figure 9. There is an obvious increase in mean glacier SLA over time, with a maximum increase from 5120 ± 159 m in 1993 to 5320 ± 240 m in 2013, which indicates that these glaciers were in a state of mass loss during the analysis period. Linear regression analysis of the SLA time series revealed a 123-m increase in mean SLA across this region during the 1989–2019 period.
We calculated the precipitation and mean temperature from the June–August (summer) observations at Tashkurgan weather station since the Karakoram Mountains experience both summer accumulation and ablation (Figure 9). The summer precipitation and temperature in the Karakoram Mountains both exhibited increasing trends over the study period. Temperature may therefore contribute to the increase in glacier SLA. The mean SLA across the Karakoram Mountains during the 1989–2019 period exhibited a strong positive correlation with summer mean temperature. The lowest SLA was observed in 1993, followed by an SLA of 5140 ± 171 m in 2000. The lowest summer mean temperature occurred in 1989. However, the difference in SLA between 2000 and 2004 was only 20 m, which was within the uncertainties of the SLA derivation. The highest glacier SLA was observed in 2013, when the mean summer mean temperature was 17.23 °C and there was relatively little precipitation (~50 mm). The correlation coefficients between mean glacier SLA and the summer mean temperature and summer precipitation in the Karakoram Mountains were 0.41 and 0.03, respectively. The mean SLA across the Karakoram Mountains during the 1989–2019 period exhibited an obvious positive correlation with summer mean temperature. The linear trends in summer mean temperature and mean SLA further suggest that temperature is the primary factor influencing the observed glacier SLA changes across the Karakoram Mountains.

4.4. Glacier SLA across the Western Himalayas

The glacier SLA across the Western Himalayas is presented in Table 5. The SLA varied by 970 m, ranging from 4560 m at H12 Glacier in 1989 to 5530 m at H3 Glacier in 2002. The SLA changes for individual glaciers during the 1989–2018 period are shown in Figure 10. Each analyzed glacier exhibited an increasing SLA trend in the Western Himalayas during the 1989–2018 period (Figure 10a), with glacier SLA increases of 60–357 m. H7 and H1 glaciers exhibited the smallest and largest increases, respectively, with most glaciers exhibiting SLA increases in the 100–300 m range. H1 Glacier also exhibited the largest SLA variability (SD = 207 m; Figure 10b), whereas H4 Glacier possessed a relatively stable SLA during the 1989–2018 period (SD = 94 m). H3 Glacier exhibited the highest mean SLA at 5320 ± 173 m, and H2 Glacier exhibited the lowest mean SLA at 4960 ± 173 m.
The mean SLA across the Western Himalayas at the end of the melt season (generally August) during the 1989–2018 period is shown in Figure 11. The mean SLA exhibited a gradual increase over time, which indicates that these glaciers were in a state of mass loss during the analysis period. The maximum and minimum SLAs were 4910 ± 190 m in 1989 and 5380 ± 164 m in 2000, respectively. Linear regression analysis of the SLA time series revealed that the mean SLA increased from 5110 m to 5300 m across the Western Himalayas during the 1989–2018 period.
We calculated both the precipitation and mean temperature from the June–August (summer) observations at the Purang weather station since the Western Himalayas experience both summer accumulation and ablation (Figure 11). The mean summer mean temperature and precipitation both exhibited increasing trends in the Western Himalayas during the analysis period, suggesting that temperature was the main cause of the increasing SLA across the Western Himalayas during the 1989–2018 period. The mean temperature was above 12.5 °C for most of the time series, ranging from 12.6 °C in 1992 to 14.4 °C in 2006.
The mean glacier SLA across the Western Himalayas during the 1989–2018 period exhibited a positive correlation with summer mean temperature (r = 0.54), which suggests that the summer mean temperature across the Western Himalayas is the main factor influencing glacier SLA. The observed relationship between glacier SLA and temperature further supports the influence of summer mean temperature on glacier SLA across the Western Himalayas.

4.5. Glacier SLA across the Gongga Mountains

The SLA for each of these glaciers is shown in Table 6. The mean SLA of each analyzed glacier exhibited a remarkable increasing trend, ranging from 188 m at G5 Glacier to 405 m at G2 Glacier (Figure 12a), with four glaciers exhibiting an increase in SLA of more than 300 m during the 30-year analysis period. The SLA varied by 630 m across the Gongga Mountains, ranging from 4810 m at G2 Glacier in 1998 to 5440 m at G3 Glacier in 2012. G2 Glacier exhibited the largest SLA variability (SD = 180 m; Figure 12b), whereas G5 Glacier exhibited the smallest SLA variability (SD = 82 m). G3 Glacier exhibited the highest mean SLA at 5180 ± 149 m, and G5 Glacier exhibited the lowest mean SLA at 5060 ± 82 m.
The mean glacier SLA across the Gongga Mountains at the end of the melt season (generally August) during the 1989–2019 period is shown in Figure 13. The mean SLA generally increased over time, which indicates that these glaciers were in a state of mass loss during the 30-year analysis period. The mean SLA varied by 540 m, ranging from 4960 ± 70 m in 1989 to 5330 ± 100 m in 2012. Linear regression analysis revealed a mean SLA increase of 282 m across the Gongga Mountains during the 1989–2019 period.
Meteorological data from the Kangding weather station, which is the closest weather station to the Gongga Mountains, were analyzed to determine the effects of temperature and precipitation on glacier SLA. We calculated the summer (June–August) precipitation and mean temperature since the glaciers across the Gongga Mountains experience both accumulation and strong ablation during the summer months (Figure 13). Increasing trends are observed in both the summer mean temperature and precipitation values, suggesting that increasing temperatures may be accelerating ablation, resulting in the increasing SLAs across the Gongga Mountains during the 1989–2019 period. The mean SLA across the Gongga Mountains during the 1989–2019 period exhibited a positive correlation with summer mean temperature (r = 0.44), which indicates that the glacier SLA across the Gongga Mountains area was primarily influenced by temperature.

4.6. Glacier SLA for Different Orientations across the Westerlies and the Monsoon Control Zone

Due to spatial variation of entire mountains ranges and differences in the number of glaciers in various orientations, uncertainty exists in the discussion of SLA changes in different orientations. Therefore, we selected the SLA of different orientations of peaks where the glaciers are concentrated to analyze the influence of the windward slope of the westerlies and monsoon water vapor in the westerly wind belt. The Tian Shan and the Nyainqentanglha Mountains were selected to represent glaciers influenced by the westerlies and the monsoon, respectively. A total of 42 glaciers in the Tian Shan and 37 glaciers in the Nyainqentanglha Mountains were selected. The number of glaciers distributed in different orientations are listed in Table 7, and their mean SLA are calculated (Figure 14).
The mean SLA of the Tian Shan glaciers toward the east is higher than that toward the west because the Tian Shan climate is dominated by the westerlies. The glaciers facing west are located on the windward slope, where the airstream that comes from the western or northwestern direction is blocked, and precipitation is thus greater than in the east. This leads to lower SLA in the west of the glaciers compared to the east. At the same time, the mean SLA of the southward glaciers is higher than that of the northward glaciers. This is because the southern slope receives more solar radiation than the northern slope, as well as that the southern side is affected by the dry and hot climate of the Tarim Basin desert in summer. Furthermore, SLA differences between southward and northward glaciers are much greater than that of the eastward and westward glaciers, probably indicating that the effect of temperature on SLA is greater than the effect of precipitation on SLA.
The mean SLA of the southward glacier in the Nyainqentanglha Mountains is lower than that of the northward glacier. The selected glaciers are concentrated in the eastern segment of the Nyainqentanglha Mountains, where they converge with the Hengduan Mountains to form a trumpet-shaped terrain, its climate is mainly controlled by the Indian monsoon, and the southern slope of the mountain constitutes a barrier of the Indian monsoon moving north. The south slope is the windward slope with more precipitation than the northern slope (rain shadow zone), resulting in lower SLA of the southward glacier than that of the northward glaciers. The SLA of the eastward glaciers is higher than that of the westward glacier because the solar radiation on the eastern slope is higher than that of the western slope. The SLA differences between the eastward and westward glaciers are greater than those toward the south and north glaciers. This probably also indicates that temperature is also the main factor that affects the SLA of the Nyainqentanglha Mountains.
There was a sharp decrease in precipitation from the eastern and southeastern marginal mountains of the Tibetan Plateau to the west and northwest during the 1989–2019 period, whereas the maximum temperature occurred in the western region of the Tibetan Plateau. Regional hydrological conditions could therefore cause an east (southeast) to west (northwest) increase in glacier SLA, as shown in Figure 15, where the maximum glacier SLA occurred on the northern slopes of the Western Himalayas. The SLAs on the eastern side of the plateau were lower and exhibited an east-to-west longitudinal pattern of increasing glacier SLA. Glacier SLA generally increased with decreasing latitude from the Altai Mountains to the Karakoram Mountains; conversely, glacier SLA decreased with decreasing latitude across the Himalayan region. The glacier SLA across the Altai Mountains was mainly influenced by the westerly wind zone. The glacier scale to the east of the distribution center of the main glaciers formed by Friendship Peak and Kuitun Peak decreased with decreasing mountain height and annual precipitation, resulting in an increase in glacier SLA from 3100 m in the Burqin River Basin to 3800 m in the Ulungu River Basin. The glacier SLA across the Karakoram Mountains gradually increased from west to east, ranging from 5000 to 5800 m, with the western section being significantly influenced by the westerly flow zone. The Himalayan SLA ranged from 5800 m on the northern slope to 4700 m on the southern slope. The Himalayas block the northward flow of the Indian monsoon zone, leading to the northern slope and more northerly region being drier than the southern slope. The Himalayan SLA therefore exhibited an abnormal SLA distribution, with low glacier SLAs on the southern slope and high glacier SLAs on the northern slope. The glacier SLA across the Hengduan Mountains was in the 4900–5200 m range. The western part of the Hengduan Mountains is located in the water vapor transport zone of the southeast monsoon, with abundant precipitation causing the glacier SLAs to extend upglacier in a tongue shape, revealing a gradual increase in SLA from the outside to the inside of a given glacier. The glacier SLAs on the eastern side of the Hengduan Mountains exhibited a longitudinal SLA pattern, with an east-to-west increase in glacier SLA.

5. Conclusions

Glacier SLA is an indicator of glacier ELA, which is a key parameter for predicting climate behavior and change. We derived the glacier SLA across High Mountain Asia and analyzed the observed SLA changes, and their relationship to temperature and precipitation observations over the past ~30 years. The selected glaciers are largely located in regions where the climate is controlled by the westerlies and/or monsoons.
Our results demonstrate that summer mean temperature is the primary factor influencing the observed glacier SLA changes across High Mountain Asia, with precipitation also playing a major role in some regions.
The mean SLA across the Altai Mountains, Karakoram Mountains, Western Himalayas, and Gongga Mountains increased during the 1989–2019 period. The mean glacier SLA across the Altai Mountains ranged from 2860 ± 169 m to 3200 ± 152 m, and the mean glacier SLA across the Karakoram Mountains varied from 5120 ± 159 m in 1993 to 5320 ± 240 m in 2013, with the glaciers across both regions experiencing an average SLA increase of 123–151 m over the past 30 years. The mean glacier SLA across the Western Himalayas and Gongga Mountains increased by 190–282 m over the past 30 years, with the mean SLA across the Western Himalayas ranging from 4910 ± 190 m in 1989 to 5380 ± 164 m in 2000, and that across the Gongga Mountains increasing from 4960 ± 70 m to 5330 ± 100 m. The was a general increase in glacier SLA from the Altai Mountains to the Karakoram Mountains, with a decrease in glacier SLA with decreasing latitude across the Himalayas; the maximum SLA occurred near the northern slopes of the Western Himalayas. The glacier SLAs were in the 3100–3800, 5000–5800, 5800–4700, and 4900–5200 m ranges across the Altai Mountains, Karakoram Mountains, Western Himalayas, and Hengduan Mountains, respectively. Correlation analyses between glacier SLA and temperature/precipitation suggested that the mean glacier SLAs in the study areas were mainly influenced by temperature. Furthermore, the glacier SLA in the westerlies (Tian Shan) and monsoon control zones (Nyainqentanglha Mountains) are affected by both temperature and precipitation. However, temperature appears to generally play a more important role than precipitation.
The accuracy in mapping glacier SLA depends on the quality of the remote-sensing image, precision of the resultant DEM, and extraction method. Since optical remote sensing is greatly influenced by cloud cover, which is especially prevalent in the southeastern Tibetan imagery, future work should include further improvements in mapping glacier SLA across these poorly imaged regions, and then extending this methodology to the entire High Mountain Asia region to better capture regional climate change, and provide more accurate constraints for mass balance studies and for snowmelt runoff and hydrological models.

Author Contributions

Methodology, Z.G.; software, A.C.; validation, N.W. and B.S.; investigation, Y.W.; writing—original draft preparation, Z.G.; writing—review and editing, L.G., B.S., and N.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (grant numbers XDA20060201, XDA19070302), the National Natural Science Foundation of China (Grant No. 41501069), and the Second Tibetan Plateau Scientific Expedition and Research Program (2019QZKK0201).

Institutional Review Board Statement

Ethical review and approval were waived for this study, due to studies not involving humans or animals.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

We thank the EROS Data Center-NASA/USGS and Geospatial data cloud for the use of available satellite imagery. We would also like to thank the China Meteorological Data Service Center for providing the meteorological data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Immerzeel, W.W.; Beek, L.P.H.V.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
  2. Chen, X.Y.; Zhang, X.B.; Church, J.A.; Watson, C.S.; King, M.A.; Monselesan, D.; Legresy, B.; Harig, C. The Increasing Rate of Global Mean Sea-Level Rise during 1993–2014. Nat. Clim. Chang. 2017, 7, 492–495. [Google Scholar] [CrossRef]
  3. Wang, W.C.; Xiang, Y.; Gao, Y.; Lu, A.X.; Yao, T.D. Rapid Expansion of Glacial Lakes Caused by Climate and Glacier Retreat in The Central Himalayas. Hydrol. Process. 2015, 29, 859–874. [Google Scholar] [CrossRef]
  4. Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Brahmbhatt, R.M.; Bahuguna, I.; Rathore, B.P.; Kulkarni, A.V.; Shah, R.D.; Nainwal, H.C.; Prof, A. Variation of Snowline and Mass Balance of Glaciers of Warwan and Bhut Basins of Western Himalaya Using Remote Sensing Technique. J. Indian Soc. Remote 2012, 40, 629–637. [Google Scholar] [CrossRef]
  6. Rabatel, A.; Dedieu, J.P.; Vincent, C. Spatio-Temporal Changes in Glacier-Wide Mass Balance Quantified by Optical Remote Sensing on 30 Glaciers in the French Alps for the Period 1983–2014. J. Glaciol. 2016, 62, 1153–1166. [Google Scholar] [CrossRef] [Green Version]
  7. Zhang, Z.M.; Jiang, L.M.; Liu, L.; Sun, Y.F.; Wang, H.S. Annual Glacier-Wide Mass Balance (2000–2016) of the Interior Tibetan Plateau Reconstructed from MODIS Albedo Products. Remote Sens. 2018, 10, 1031. [Google Scholar] [CrossRef] [Green Version]
  8. Paterson, W.S.B. The Physics of Glaciers, 3rd ed.; Elsevier Science: Oxford, UK, 1994. [Google Scholar]
  9. Rabatel, A.; Bermejo, A.; Loarte, E.; Soruco, A.; Gomez, J.; Leonardini, G.; Vincent, C.; Sicart, J.E. Can the Snowline Be Used as an Indicator of the Equilibrium Line and Mass Balance for Glaciers in the Outer Tropics? J. Glaciol. 2012, 58, 1327–1336. [Google Scholar] [CrossRef] [Green Version]
  10. Mernild, S.H.; Pelto, M.; Malmros, J.K.; Yde, J.C.; Knudsen, N.T.; Hanna, E. Identification of Snow Ablation Rate, ELA, AAR and Net Mass Balance Using Transient Snowline Variations on two Arctic Glaciers. J. Glaciol. 2013, 59, 649–659. [Google Scholar] [CrossRef] [Green Version]
  11. Rabatel, A.; Dedieu, J.P.; Vincent, C. Using Remote-Sensing Data to Determine Equilibrium-Line Altitude and Mass-Balance Time Series: Validation on Three French Glaciers, 1994–2002. J. Glaciol. 2005, 51, 539–546. [Google Scholar] [CrossRef] [Green Version]
  12. Rees, W.G. Remote Sensing of Snow and Ice, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
  13. De Angelis, H.; Rau, F.; Skvarca, P. Snow Zonation on Hielo Patagónico Sur, Southern Patagonia, Derived from Landsat 5 TM Data. Glob. Planet. Chang. 2007, 59, 149–158. [Google Scholar] [CrossRef]
  14. Hu, Z.Y.; Dietz, A.; Kuenzer, C. The Potential of Retrieving Snow Line Dynamics from Landsat during the End of the Ablation Seasons between 1982 and 2017 in European Mountains. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 138–148. [Google Scholar] [CrossRef]
  15. McFadden, E.M.; Ramage, J.M.; Rodbell, D. Landsat TM and ETM+ Derived Snowline Altitudes in the Cordillera Huayhuash and Cordillera Raura, Peru, 1986–2005. Cryosphere 2011, 5, 419–430. [Google Scholar] [CrossRef] [Green Version]
  16. Guo, Z.M.; Wang, N.L.; Wu, H.B.; Wu, Y.W.; Wu, X.J.; Li, Q.L. Variations in Firn Line Altitude and Firn Zone Area on Qiyi Glacier, Qilian Mountains, over the Period of 1990 to 2011. Arct. Antarct. Alp. Res. 2015, 47, 293–300. [Google Scholar] [CrossRef] [Green Version]
  17. Pelto, M. Utility of Late Summer Transient Snowline Migration Rate on Taku Glacier, Alaska. Cryosphere 2011, 5, 1127–1133. [Google Scholar] [CrossRef]
  18. Zhang, Q.B.; Kang, S.C. Glacier Snowline Altitude Variations in the Pamirs, Tajikistan, 1998–2013: Insights from Remote Sensing Images. Remote Sens. Lett. 2017, 8, 1220–1229. [Google Scholar] [CrossRef]
  19. Kaur, R.; Saikumar, D.; Kulkarni, A.V.; Chaudhary, B.S. Variations in Snowcover and Snowline Altitude in Baspa Basin. Curr. Sci. India 2009, 96, 1255–1258. [Google Scholar]
  20. Guo, Z.M.; Wang, N.L.; Kehrwald, N.M.; Mao, R.J.; Wu, H.B.; Wu, Y.W.; Jiang, X. Temporal and Spatial Changes in Western Himalayan Firn Line Altitudes from 1998 to 2009. Glob. Planet. Chang. 2014, 118, 97–105. [Google Scholar] [CrossRef]
  21. Chen, M.D. Spatio-temporal Change Dynamic of Snowline on Tibetan Plateau; Lanzhou University: Lanzhou, China, 2014. [Google Scholar]
  22. Shi, J.; Bai, S.; Gao, J.; Gu, H. Spatial and Temporal Variation of Snow Line and Its Relationships with Meteorological Factors in Tibet Plateau in Recent 10 Years. Desert Oasis Meteorol. 2015, 9, 7–13. [Google Scholar]
  23. Tang, Z.; Wang, J.; Liang, J.; Li, C.; Wang, X. Monitoring of Snowline Altitude over the Tibetan Plateau Based on MODIS Data. Remote Sens. Technol. Appl. 2015, 30, 767–774. [Google Scholar]
  24. Bao, W.J.; Liu, S.Y.; Wu, K.P.; Wang, R.J.; Jiang, Z.L. A Method for Extracting Snow Line Altitude Based on MODIS Snow Product. J. Glaciol. Geocryol. 2017, 39, 259–272. [Google Scholar]
  25. Consortium, RGI. Randolph Glacier Inventory–A Dataset of Global Glacier Outlines: Version 5.0: Technical Report, Global Land Ice Measurements from Space, Boulder Colorado, the United States of America. 2015. Digital Media. Available online: www.glims.org/RGI (accessed on 15 December 2020).
  26. Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different Glacier Status with Atmospheric Circulations in Tibetan Plateau and Surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
  27. Xie, Z.; Zhou, Z.; Li, Q.; Wang, S. Progress and Prospects of Mass Balance Characterist and Responding to Global Change of Glacier System in High Asia. Adv. Earth Sci. 2009, 24, 1065–1072. [Google Scholar]
  28. Shih, Y.; Hsieh, T.; Cheng, P.H.; Li, C. Distribution, Features and Variations of Glaciers in China World Glacier Inventory; IAHS–AISH, Dorking, Eng.: International Association of Hydrological Sciences: Riederalp, Switzerland, 1980; Volume 126, pp. 111–116. [Google Scholar]
  29. Lanzhou Institute of Glaciology and Cryopedology; Chinese Academy of Sciences. An Introduction to the Glaciers in China; Science Press: Beijing, China, 1988. [Google Scholar]
  30. Tang, Z.; Wang, X.; Wang, J.; Wang, X.; Wei, J. Investigating Spatiotemporal Patterns of Snowline Altitude at the End of Melting Season in High Mountain Asia, Using Cloud-Free MODIS Snow Cover Product, 2001–2016. Cryosphere Discuss. 2019. Available online: https://tc.copernicus.org/preprints/tc-2019-139/ (accessed on 15 December 2020).
  31. Greuell, W.; Reijmer, C.H.; Oerlemans, J. Narrowband-to-Broadband Albedo Conversion for Glacier Ice and Snow Based on Aircraft and Near-Surface Measurements. Remote Sens. Environ. 2002, 82, 48–63. [Google Scholar] [CrossRef]
  32. Liang, S. Narrowband to Broadband Converions of Land Surface Albedo: I Algorithms. Remote Sens. Environ. 2000, 76, 213–238. [Google Scholar] [CrossRef]
  33. Naegeli, K.; Damm, A.; Huss, M.; Wulf, H.; Schaepman, M.; Hoelzle, M. Cross-Comparison of Albedo Products for Glacier Surfaces Derived from Airborne and Satellite (Sentinel-2 and Landsat 8) Optical Data. Remote Sens. 2017, 9, 110. [Google Scholar] [CrossRef] [Green Version]
  34. Mao, R.J.; Jiang, X.; Guo, Z.M.; Wu, H.B.; Wang, S. Study of the Inversion Precision of Albedo on the Qiyi Glacier in the Qilian Mountain Based on TM/ETM+ Image. J. Glaciol. Geocryol. 2013, 35, 301–309. [Google Scholar]
Remotesensing 13 00425 g001 550
Figure 1. Location of the study area and primary wind circulation patterns. The black triangle represents the glaciers located in the Altai Mountains, the Karakoram Mountains, the Western Himalayas and the Gongga Mountains to identify the snowline altitude (SLA).
Figure 1. Location of the study area and primary wind circulation patterns. The black triangle represents the glaciers located in the Altai Mountains, the Karakoram Mountains, the Western Himalayas and the Gongga Mountains to identify the snowline altitude (SLA).
Remotesensing 13 00425 g001
Remotesensing 13 00425 g002 550
Figure 2. Temporal distribution of the selected Landsat images to derive SLA.
Figure 2. Temporal distribution of the selected Landsat images to derive SLA.
Remotesensing 13 00425 g002
Remotesensing 13 00425 g003 550
Figure 3. The distribution of bare ice and snow-covered areas based on appreciably different albedo on the Shamshar gang glacier in Western Himalayan in 1998, 2000, 2002, 2007, and 2009 [20].
Figure 3. The distribution of bare ice and snow-covered areas based on appreciably different albedo on the Shamshar gang glacier in Western Himalayan in 1998, 2000, 2002, 2007, and 2009 [20].
Remotesensing 13 00425 g003
Remotesensing 13 00425 g004 550
Figure 4. Landsat- and MODIS-derived SLA time series, with the Landsat-derived SLAs taken as the “true values” (example from the Western Himalayas presented). SLAModis, SLALandsat, and SLAModis-Landsat represent the MODIS-derived SLA, Landsat-derived SLA, and Landsat-derived SLA with MODIS interpolation, respectively.
Figure 4. Landsat- and MODIS-derived SLA time series, with the Landsat-derived SLAs taken as the “true values” (example from the Western Himalayas presented). SLAModis, SLALandsat, and SLAModis-Landsat represent the MODIS-derived SLA, Landsat-derived SLA, and Landsat-derived SLA with MODIS interpolation, respectively.
Remotesensing 13 00425 g004
Remotesensing 13 00425 g005 550
Figure 5. Glacier SLAs that were extracted from the Sentinel-2 images during the ablation season.
Figure 5. Glacier SLAs that were extracted from the Sentinel-2 images during the ablation season.
Remotesensing 13 00425 g005
Remotesensing 13 00425 g006 550
Figure 6. (a) SLA changes and (b) mean SLA of the 12 analyzed glaciers across the Altai Mountains during the 1989–2019 period. The error bars in (b) represent one standard deviation from the mean.
Figure 6. (a) SLA changes and (b) mean SLA of the 12 analyzed glaciers across the Altai Mountains during the 1989–2019 period. The error bars in (b) represent one standard deviation from the mean.
Remotesensing 13 00425 g006
Remotesensing 13 00425 g007 550
Figure 7. Cold season (September–May) precipitation (blue), summer mean temperature (red), and glacier SLA (black) across the Altai Mountains during the 1989–2019 period. Dashed lines indicate the best-fit linear trends for each dataset.
Figure 7. Cold season (September–May) precipitation (blue), summer mean temperature (red), and glacier SLA (black) across the Altai Mountains during the 1989–2019 period. Dashed lines indicate the best-fit linear trends for each dataset.
Remotesensing 13 00425 g007
Remotesensing 13 00425 g008 550
Figure 8. (a) SLA changes and (b) mean SLA of the nine analyzed glaciers across the Karakoram Mountains during the 1989–2019 period. The error bars in (b) represent one standard deviation from the mean.
Figure 8. (a) SLA changes and (b) mean SLA of the nine analyzed glaciers across the Karakoram Mountains during the 1989–2019 period. The error bars in (b) represent one standard deviation from the mean.
Remotesensing 13 00425 g008
Remotesensing 13 00425 g009 550
Figure 9. Summer precipitation (blue), summer mean temperature (red), and glacier SLA (black) across the Karakoram Mountains during the 1989–2019 period. Dashed lines indicate the best-fit linear trends for each dataset.
Figure 9. Summer precipitation (blue), summer mean temperature (red), and glacier SLA (black) across the Karakoram Mountains during the 1989–2019 period. Dashed lines indicate the best-fit linear trends for each dataset.
Remotesensing 13 00425 g009
Remotesensing 13 00425 g010 550
Figure 10. (a) SLA changes and (b) mean SLA for the12 analyzed glaciers across the Western Himalayas during the 1989–2018 period. The error bars in (b) represent one standard deviation from the mean.
Figure 10. (a) SLA changes and (b) mean SLA for the12 analyzed glaciers across the Western Himalayas during the 1989–2018 period. The error bars in (b) represent one standard deviation from the mean.
Remotesensing 13 00425 g010
Remotesensing 13 00425 g011 550
Figure 11. Summertime precipitation (blue) and temperature (red), and glacier SLA (black) across the Western Himalayas during the 1989–2018 period. Dashed lines indicate the best-fit linear trends to each dataset.
Figure 11. Summertime precipitation (blue) and temperature (red), and glacier SLA (black) across the Western Himalayas during the 1989–2018 period. Dashed lines indicate the best-fit linear trends to each dataset.
Remotesensing 13 00425 g011
Remotesensing 13 00425 g012 550
Figure 12. (a) SLA changes and (b) mean SLA of the five analyzed glaciers across the Gongga Mountains during the 1989–2019 period. Error bars in (b) represent one standard deviation from the mean.
Figure 12. (a) SLA changes and (b) mean SLA of the five analyzed glaciers across the Gongga Mountains during the 1989–2019 period. Error bars in (b) represent one standard deviation from the mean.
Remotesensing 13 00425 g012
Remotesensing 13 00425 g013 550
Figure 13. Summer precipitation (blue), summer mean temperature (red), and glacier SLA (black) across Gongga Mountains during the 1989–2019 period. Dashed lines indicate the best-fit linear trends for each dataset.
Figure 13. Summer precipitation (blue), summer mean temperature (red), and glacier SLA (black) across Gongga Mountains during the 1989–2019 period. Dashed lines indicate the best-fit linear trends for each dataset.
Remotesensing 13 00425 g013
Remotesensing 13 00425 g014 550
Figure 14. Glacier SLA in different orientations in the Tian Shan and the Nyainqentanglha Mountains.
Figure 14. Glacier SLA in different orientations in the Tian Shan and the Nyainqentanglha Mountains.
Remotesensing 13 00425 g014
Remotesensing 13 00425 g015 550
Figure 15. Glacier SLA variations across different mountainous regions of the Tibetan Plateau.
Figure 15. Glacier SLA variations across different mountainous regions of the Tibetan Plateau.
Remotesensing 13 00425 g015
Table
Table 1. Landsat MSS/TM/ETM+/OLI data used for mapping SLA.
Table 1. Landsat MSS/TM/ETM+/OLI data used for mapping SLA.
Study RegionPath/RowSensorDateData Source
The Altai Mountains144/26MSS1989/8/17USGS
TM51993/8/12USGS
TM51996/8/20USGS
TM51998/8/26USGS
ETM+2000/8/7GSCloud
ETM+2001/8/10USGS
ETM+2004/8/18GSCloud
ETM+2006/7/23GSCloud
TM52007/8/3USGS
ETM+2008/8/13GSCloud
TM52009/8/8GSCloud
TM52010/8/27GSCloud
ETM+2012/8/24GSCloud
ETM+2013/8/27USGS
OLI2015/7/24GSCloud
OLI2016/8/25GSCloud
OLI2017/8/14USGS
OLI2019/8/4USGS
The Karakoram Mountains148/35TM 51991/8/19USGS
TM51993/7/7USGS
TM51994/7/26USGS
TM51996/8/16USGS
TM51997/7/18USGS
TM51999/8/9USGS
TM52000/8/27USGS
ETM+2001/7/21USGS
ETM+2002/8/9USGS
ETM+2004/8/14USGS
ETM+2005/9/2USGS
ETM+2006/8/20USGS
ETM+2007/8/23USGS
ETM+2009/8/12USGS
ETM+2010/8/31USGS
TM52011/8/10GSCloud
OLI2013/7/30USGS
ETM+2014/7/25USGS
OLI2015/8/21USGS
ETM+2017/8/18USGS
ETM+2018/8/21USGS
OLI2019/8/16USGS
The Himalayas147/37TM51989/8/6USGS
TM51991/8/28USGS
TM51992/8/14USGS
TM51993/9/2USGS
TM51994/8/20USGS
TM51998/8/31USGS
ETM+2000/8/28GSCloud
ETM+2002/8/2GSCloud
ETM+2004/9/8USGS
ETM+2007/8/16USGS
TM 52009/8/13USGS
ETM+2011/9/12USGS
OLI2013/7/23GSCloud
OLI2014/8/11USGS
OLI2015/9/15GSCloud
OLI2016/8/16USGS
OLI2018/8/22USGS
The Gongga Mountains131/39TM51989/6/19USGS
TM51990/7/8USGS
TM51994/8/4USGS
TM51995/8/7USGS
TM51997/7/27USGS
TM51998/7/30USGS
TM51999/8/2USGS
TM52000/8/20USGS
ETM+2003/8/5USGS
ETM+2006/7/28USGS
TM52007/8/8USGS
ETM+2009/8/21USGS
ETM+2010/8/8USGS
ETM+2011/8/11USGS
ETM+2012/8/13USGS
OLI2013/7/7USGS
OLI2014/7/26USGS
OLI2016/8/24USGS
ETM+2019/8/17USGS
Table
Table 2. Information on the nearest meteorological stations to the analyzed glacier areas.
Table 2. Information on the nearest meteorological stations to the analyzed glacier areas.
Station IDNameLatitudeLongitudeElevation (m)Study Area
52633Tuole38°48′98°25′3368Qiyi Glacier
51053Haba River48°03′86°24′533Altai Mountains
51804Tashkurgan37°27′75°08′3090Karakoram Mountains
55437Purang30°17′81°15′3900Western Himalayas
56374Kangding30°1.8′101°34′2616Gongga Mountains
Table
Table 3. SLAs for the 12 analyzed glaciers across the Altai Mountains during the 1989–2019 period.
Table 3. SLAs for the 12 analyzed glaciers across the Altai Mountains during the 1989–2019 period.
YearSLA (m)
A1A2A3A4A5A6A7A8A9A10A11A12
1989288029303270300029502880321033203080308029002990
199328402860NA291028202760319030702920303028503040
1996260029402980284027302770321030202820297027402700
1998304031203150321029403110329034403310335030003300
2000275031203140311029702970310033203200326029903240
2001NANA319030903010NA324034403190326029803180
2004303031103160NANA3040331034303250NA29703230
2006275030503100295029602880304033003180324029003170
20073060NANA30603000NA323034803200329029703170
2008302031403140312029902850309032103080322030003240
2009274030303090296029202820307033903090312029003036
2010307030703250307029602920320034703070319029803030
2012310031603180327029602920329033803300341031303250
201327303010NA30903140NA321033803140318029103050
2015296031103170303029302920322035403220328029603090
2016302031403180310030102960327034803280333029803280
2017309031303200312030302940323034703330331031303240
201929803110NA305029702930326034603280333029903270
Table
Table 4. SLA of the nine analyzed glaciers across the Karakoram Mountains during the 1989–2019 period.
Table 4. SLA of the nine analyzed glaciers across the Karakoram Mountains during the 1989–2019 period.
YearSnowline Altitude (m)
K1K2K3K4K5K6K7K8K9
1991521051905070520055005060508051105150
1993511049004950509053705010519051605330
1994513051305050498054605310522051205180
199650305120NA552055405170524054005440
1997519051005070513054805210520052305420
19995050NANANANANA525054205490
2000506051504920522054205060NANANA
2001507051704970535054705290523052705330
2002504052004800530056405270NA53005480
200450305140485051605510519052005110NA
2005505051504930529054905280523053405340
2006506052005040537055505390526054305490
200750505190NA5290NA5300NANA5410
2009504051504800521054405250523054905510
2010504051404710523054705260526055305390
201150605160NA511055205240524054305540
2013NA51604880531055105300526056605490
2014519051405090518054905210519054405320
2015503051605100519055605240514056005320
201752005160NA522055805300523053805470
2018521051705100521056105260526053805420
2019520051805090521055805260526055805290
Table
Table 5. SLAs of the 12 analyzed glaciers across the Western Himalayas during the 1989–2018 period.
Table 5. SLAs of the 12 analyzed glaciers across the Western Himalayas during the 1989–2018 period.
YearSnowline Altitude (m)
H1H2H3H4H5H6H7H8H9H10H11H12
1989465047204850507049805090510048105010492051304560
1991NA48905250523516052005250NA5060519050804900
19924890488051605130504052205310NA5030506049504840
1993515047905180516053405190525048304990492050004860
1994497048905220525053605300523051605090502050404880
1998529048905230527053105320529051905170518053004870
2000550049205500543054605460542052905370552054405290
2002531049705530531054205370534052405310530053305330
2004531049605460538054205460534052205150528053804970
2007529051005500529053705410533052705290523053605130
2009510050105410525053705240524052105110519052604940
2011520054005270524052405240523051705090516052604860
201351204950533052505380526050405200506052105140NA
20145230493052505260NA52505380NA5180521052104900
20155270498054105380511053005290NA5350522053104890
2016521050805440530054005350534052505220530053705300
2018541049405480539054305460535052605290537053905000
Table
Table 6. SLA of the five analyzed glaciers across the Gongga Mountains during the 1989–2019 period.
Table 6. SLA of the five analyzed glaciers across the Gongga Mountains during the 1989–2019 period.
YearSnowline Altitude (m)
G1G2G3G4G5
198949704840500049705020
199049804870504050604960
199451604970506049905030
199551205020508050805070
1997503048304980NA4980
1998523048105220NA5000
199951605040511051504980
200051805060518050205050
200350905070510050105010
2006525053505370NANA
200751505150511050005040
200952405290530053105100
201053105310543053205120
201151105120503053005090
20125290NA5440NA5250
2013518053705150NA5040
2014513050605070NANA
201652504980536053205070
201953205240531053505240
Table
Table 7. The number of glaciers in different orientations in the Tian Shan and the Nyainqentanglha Mountains.
Table 7. The number of glaciers in different orientations in the Tian Shan and the Nyainqentanglha Mountains.
Study AreaNumber of Glaciers in Different Orientations
NESW
Tian Shan2291215
Nyainqentanglha Mountains20221511
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Guo, Z.; Geng, L.; Shen, B.; Wu, Y.; Chen, A.; Wang, N. Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors. Remote Sens. 2021, 13, 425. https://doi.org/10.3390/rs13030425

AMA Style

Guo Z, Geng L, Shen B, Wu Y, Chen A, Wang N. Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors. Remote Sensing. 2021; 13(3):425. https://doi.org/10.3390/rs13030425

Chicago/Turabian Style

Guo, Zhongming, Lei Geng, Baoshou Shen, Yuwei Wu, Anan Chen, and Ninglian Wang. 2021. "Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors" Remote Sensing 13, no. 3: 425. https://doi.org/10.3390/rs13030425

APA Style

Guo, Z., Geng, L., Shen, B., Wu, Y., Chen, A., & Wang, N. (2021). Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors. Remote Sensing, 13(3), 425. https://doi.org/10.3390/rs13030425

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop