Data Assimilation for Rainfall-Runoff Prediction Based on Coupled Atmospheric-Hydrologic Systems with Variable Complexity
Abstract
:1. Introduction
- What are the differences in the improvement of rainfall before and after data assimilation for the storm events with different spatial and temporal distributions in semi-humid areas of northern China?
- What are the corresponding runoff effects of different coupling systems on the improved rainfall from WRF and its assimilation mode?
- What differences exist between the runoff processes modeled by the coupled systems of different complexity before and after assimilation?
- How does the complexity of the hydrological structure affect the transmission of rainfall improvement from data assimilation to runoff?
2. Study Area and Events
2.1. Study Area
2.2. Storm Events
3. Three Atmospheric–Hydrologic Coupled Systems
3.1. The Numerical Weather Prediction (NWP) Model
3.1.1. Weather Research Forecasting (WRF) Model Configurations
3.1.2. Data Assimilation with WRF-3DVar
3.2. Hydrological Models with Differing Complexity
3.2.1. The Lumped Hebei Model
3.2.2. The Grid-Based Hebei Model
3.2.3. The WRF-Hydro Modeling System
3.3. Establishment of Three Coupled Atmospheric-Hydrological Systems
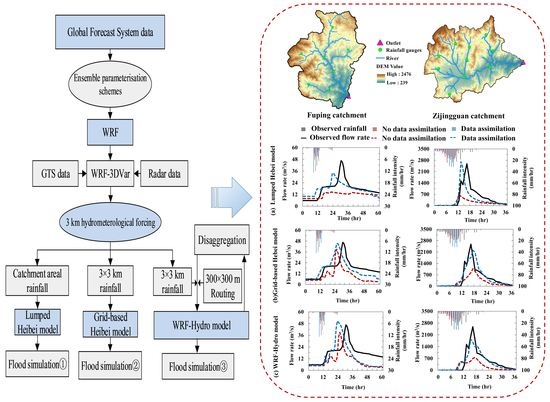
4. Results
4.1. Effect of Data Assimilation on Rainfall Prediction
4.2. Effect of Data Assimilation on Runoff Prediction
4.3. Effect of Data Assimilation on Coupled Systems with Variable Complexity
4.3.1. Results with the Lumped Hebei Model
4.3.2. Results with the Grid-Based Hebei Model
4.3.3. Results with the WRF-Hydro Modeling System
4.4. Improvement with Different Coupled Systems after Data Assimilation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, W.; Seaman, N.L. A comparison study of convective parameterization schemes in a mesoscale model. Mon. Weather Rev. 1997, 125, 252–278. [Google Scholar] [CrossRef] [Green Version]
- Yousef, L.A.; Taha, B. Adaptation of water resources management to changing climate: The role of Intensity-Duration-Frequency curves. Int. J. Environ. Dev. 2015, 6, 478. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhenming, J.I.; Chen, D.; Kang, S.; Congshen, F.U.; Duan, K.; Shen, M. Improved Land Use and Leaf Area Index Enhances WRF-3DVAR Satellite Radiance Assimilation: A Case Study Focusing on Rainfall Simulation in the Shule River Basin during July 2013. Adv. Atmos. Sci. 2018, 35, 628–644. [Google Scholar] [CrossRef]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar] [CrossRef] [Green Version]
- Bao, H.; Li, Z.; Yu, Z. Development of coupled atmospheric-hydrologic-hydraulic flood forecasting system driven by ensemble weather predictions. AGUFM 2009, 2009, H51G-0833. [Google Scholar] [CrossRef]
- Ferretti, R.; Lombardi, A.; Tomassetti, B.; Sangelantoni, L.; Colaiuda, V.; Mazzarella, V.; Maiello, I.; Verdecchia, M.; Redaelli, G. Regional ensemble forecast for early warning system over small Apennine catchments on Central Italy. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–25. [Google Scholar] [CrossRef]
- Sokol, Z. Assimilation of extrapolated radar reflectivity into a NWP model and its impact on a precipitation forecast at high resolution. Atmos. Res. 2011, 100, 201–212. [Google Scholar] [CrossRef]
- Mohanty, U.C.; Routray, A.; Osuri, K.K.; Prasad, S.K. A Study on Simulation of Heavy Rainfall Events over Indian Region with ARW-3DVAR Modeling System. Pure Appl. Geophys. 2012, 169, 381–399. [Google Scholar] [CrossRef]
- Routray, A.; Mohanty, U.; Niyogi, D.; Rizvi, S.; Osuri, K.K. Simulation of heavy rainfall events over Indian monsoon region using WRF-3DVAR data assimilation system. Meteorol. Atmos. Phys. 2010, 106, 107–125. [Google Scholar] [CrossRef]
- Kumar, P.; Varma, A.K. Assimilation of INSAT-3D hydro-estimator method retrieved rainfall for short-range weather prediction. Q. J. R. Meteorolog. Soc. 2016, 143, 384–394. [Google Scholar] [CrossRef]
- Fierro, A.O.; Clark, A.J.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R.; Ziegler, C.L. Impact of storm-scale lightning data assimilation on WRF-ARW precipitation forecasts during the 2013 warm season over the contiguous United States. Mon. Weather Rev. 2015, 143, 757–777. [Google Scholar] [CrossRef]
- Yesubabu, V.; Srinivas, C.V.; Langodan, S.; Hoteit, I. Predicting extreme rainfall events over Jeddah, Saudi Arabia: Impact of data assimilation with conventional and satellite observations. Q. J. R. Meteorolog. Soc. 2016, 142, 327–348. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.A.; Wen, L.; Lu, G.; Wu, Z.; Zhang, J.; Yang, Y.; Zhu, Y.; Tong, L. Atmospheric-hydrological modeling of severe precipitation and floods in the Huaihe River Basin, China. J. Hydrol. 2006, 330, 249–259. [Google Scholar] [CrossRef]
- Lu, G.; Wu, Z.; Wen, L.; Lin, C.A.; Zhang, J.; Yang, Y. Real-time flood forecast and flood alert map over the Huaihe River Basin in China using a coupled hydro-meteorological modeling system. Sci. China Ser. E Technol. Sci. 2008, 51, 1049–1063. [Google Scholar] [CrossRef]
- Lin, C.A.; Wen, L.; Lu, G.; Wu, Z.; Zhang, J.; Yang, Y.; Zhu, Y.; Tong, L. Real-time forecast of the 2005 and 2007 summer severe floods in the Huaihe River Basin of China. J. Hydrol. 2010, 381, 33–41. [Google Scholar] [CrossRef]
- Wu, J.; Lu, G.; Wu, Z. Flood forecasts based on multi-model ensemble precipitation forecasting using a coupled atmospheric-hydrological modeling system. Nat. Hazards 2014. [Google Scholar] [CrossRef]
- Moser, B.A.; Gallus, W.A., Jr.; Mantilla, R. An initial assessment of radar data assimilation on warm season rainfall forecasts for use in hydrologic models. Weather Forecast 2015, 30, 1491–1520. [Google Scholar] [CrossRef]
- Yang, D.; Herath, S.; Musiake, K. Comparison of different distributed hydrological models for characterization of catchment spatial variability. Hydrol. Process. 2000, 14, 403–416. [Google Scholar] [CrossRef]
- Essou, G.R.C.; Arsenault, R.; Brissette, F. Comparison of climate datasets for lumped hydrological modeling over the continental United States. J. Hydrol. 2016, 537, 334–345. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Dulal, K.N. Model trees as an alternative to neural networks in rainfall—runoff modelling. Hydrol. Sci. J. 2003, 48, 399–411. [Google Scholar] [CrossRef]
- Bray, M.; Han, D. Identification of support vector machines for runoff modelling. J. Hydroinf. 2004, 6, 265–280. [Google Scholar] [CrossRef] [Green Version]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Herath, H.M.V.V.; Chadalawada, J.; Babovic, V. Hydrologically Informed Machine Learning for Rainfall-Runoff Modelling: Towards Distributed Modelling. Hydrol. Earth Syst. Sci. Discuss. 2020, 487, 1–42. [Google Scholar] [CrossRef]
- Cho, Y.; Engel, B.A. NEXRAD Quantitative Precipitation Estimations for Hydrologic Simulation Using a Hybrid Hydrologic Model. J. Hydrometeorol. 2017, 18, 25–47. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.B.; Gochis, D.J.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.A. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Wagner, S.; Fersch, B.; Yuan, F.; Yu, Z.; Kunstmann, H. Fully coupled atmospheric-hydrological modeling at regional and long-term scales: Development, application, and analysis of WRF-HMS. Water Resour. Res. 2016. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, J.; Pan, S.; Tang, K.; Li, C.; Han, D. A real-time flood forecasting system with dual updating of the NWP rainfall and the river flow. Nat. Hazards 2015, 77, 1161–1182. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Wang, H.; Qin, J.; Li, J.; Chiao, S. Extending flood forecasting lead time in a large watershed by coupling WRF QPF with a distributed hydrological model. Hydrol. Earth Syst. Sci. 2017, 21, 1279. [Google Scholar] [CrossRef] [Green Version]
- Rogelis, M.C. Streamflow forecasts from WRF precipitation for flood early warning in mountain tropical areas. Hydrol. Earth Syst. Sci. 2018, 22, 853–870. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S.; Siddique, R.; Reed, S.; Ahnert, P.; Mejia, A. Hydrological Model Diversity Enhances Streamflow Forecast Skill at Short- to Medium-Range Timescales. Water Resour. Res. 2019, 55, 1510–1530. [Google Scholar] [CrossRef]
- Haddeland, I.; Clark, D.B.; Franssen, W.; Ludwig, F.; Voß, F.; Arnell, N.W.; Bertrand, N.; Best, M.; Folwell, S.; Gerten, D. Multimodel estimate of the global terrestrial water balance: Setup and first results. J. Hydrometeorol. 2011, 12, 869–884. [Google Scholar] [CrossRef] [Green Version]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; Van Beek, L.; Bierkens, M.F.; Blyth, E.; de Roo, A.; Döll, P.; Ek, M.; Famiglietti, J. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Li, C.; Liu, Y.; Yu, F.; Yu, E. An Evaluation Study of the Fully Coupled WRF/WRF-Hydro Modeling System for Simulation of Storm Events with Different Rainfall Evenness in Space and Time. Water 2020, 12, 1209. [Google Scholar] [CrossRef]
- Fiori, E.; Comellas, A.; Molini, L.; Rebora, N.; Siccardi, F.; Gochis, D.; Tanelli, S.; Parodi, A. Analysis and hindcast simulations of an extreme rainfall event in the Mediterranean area: The Genoa 2011 case. Atmos. Res. 2014, 138, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Verri, G.; Pinardi, N.; Gochis, D.; Tribbia, J.; Navarra, A.; Coppini, G.; Vukicevic, T. A meteo-hydrological modelling system for the reconstruction of river runoff: The case of the Ofanto river catchment. Nat. Hazards Earth Syst. Sci. 2017, 17, 1741–1761. [Google Scholar] [CrossRef] [Green Version]
- Moeng, C.H.; Dudhia, J.; Klemp, J.; Sullivan, P. Examining Two-Way Grid Nesting for Large Eddy Simulation of the PBL Using the WRF Model. Mon. Weather Rev. 2007, 135, 2295–2311. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Analysis of resolved and parameterized vertical transports in convective boundary layers at gray-zone resolutions. J. Atmos. Sci. 2013, 70, 3248–3261. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Yan, D.; Li, C.; Yu, F. Numerical rainfall simulation with different spatial and temporal evenness by using a WRF multiphysics ensemble. Nat. Hazards Earth Syst. Sci. 2017, 17, 563–579. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Liu, J.; Wang, J.; Li, C.; Yu, F.; Chu, Z. A spatio-temporal evaluation of the WRF physical parameterisations for numerical rainfall simulation in semi-humid and semi-arid catchments of Northern China. Atmos. Res. 2017, 191, 141–155. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 13, 5233–5250. [Google Scholar] [CrossRef] [Green Version]
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Liu, J.; Yan, D.; Li, C.; Chu, Z.; Yu, F. An assimilation test of Doppler radar reflectivity and radial velocity from different height layers in improving the WRF rainfall forecasts. Atmos. Res. 2017, 198, 132–144. [Google Scholar] [CrossRef]
- Liu, J.; Tian, J.; Yan, D.; Li, C.; Yu, F.; Shen, F. Evaluation of Doppler radar and GTS data assimilation for NWP rainfall prediction of an extreme summer storm in northern China: From the hydrological perspective. Hydrol. Earth Syst. Sci. 2018, 22, 4329–4348. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J. Physically based, variable contibution area model of basin hydrology. Hydrol. Ences. Bull. 1979, 24. [Google Scholar] [CrossRef] [Green Version]
- Beven, K. Surface water hydrology-runoff generation and basin structure. Rev. Geophys. 1983, 21, 721–730. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Wang, Y.; Wang, W.; Li, C.; Hu, C. A coupled atmospheric-hydrologic modeling system with variable grid sizes for rainfall-runoff simulation in semi-humid and semi-arid watersheds: How does the coupling scale affects the results? Hydrol. Earth Syst. Sci. 2020, 24, 3933–3949. [Google Scholar] [CrossRef]
- Gochis, D.J.; Chen, F. Hydrological Enhancements to the Community Noah Land Surface Model: Technical Description; NCAR Tech. Note, TN-454+STR, Boulder, Colo.; University Corporation for Atmospheric Research: Boulder, CO, USA, 2003; 77p. [Google Scholar] [CrossRef]
- Schaake, J.C.; Koren, V.I.; Duan, Q.-Y.; Mitchell, K.; Chen, F. Simple water balance model for estimating runoff at different spatial and temporal scales. J. Geophys. Res. Atmos. 1996, 101, 7461–7475. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Lettenmaier, D.P. A comparison of simplified methods for routing topographically driven subsurface flow. Water Resour. Res. 1999, 35, 255–264. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L.; Martin, W.D.; Harmon, R.S. Theory, development, and applicability of the surface water hydrologic model CASC2D. Hydrol. Process. 2002, 16, 255–275. [Google Scholar] [CrossRef]
- Gochis, D.; Barlage, M.; Dugger, A.; FitzGerald, K.; Karsten, L.; McAllister, M.; McCreight, J.; Mills, J.; RefieeiNasab, A.; Read, L. The WRF-Hydro modeling system technical description (Version 5.0). NCAR Tech. Note 2018, 107. [Google Scholar] [CrossRef]
- Moore, R. The probability-distributed principle and runoff production at point and basin scales. Hydrol. Sci. J. 1985, 30, 273–297. [Google Scholar] [CrossRef] [Green Version]
- Cuntz, M.; Mai, J.; Samaniego, L.; Clark, M.; Wulfmeyer, V.; Branch, O.; Attinger, S.; Thober, S. The impact of standard and hard-coded parameters on the hydrologic fluxes in the Noah-MP land surface model. J. Geophys. Res. Atmos. 2016, 121, 10676–10700. [Google Scholar] [CrossRef]
- Wang, Y.; Lahmers, T.; Hazenberg, P.; Gupta, H.; Castro, C.; Gochis, D.; Dugger, A.; Yates, D.; Read, L.; Karsten, L. Enhancements to the WRF-Hydro Hydrologic Model Structure for Semi-arid Environments. AGUFM 2018, 2018, H41P-2347. [Google Scholar]
- Zarekarizi, M. Ensemble Data Assimilation for Flood Forecasting in Operational Settings: From Noah-MP to WRF-Hydro and the National Water Model. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Xi, C.; Yang, T.; Wang, X.; Xu, C.Y.; Yu, Z. Uncertainty Intercomparison of Different Hydrological Models in Simulating Extreme Flows. Water Resour. Manag. 2012, 27, 1393–1409. [Google Scholar] [CrossRef]












| Storm Event | Catchment | Storm Duration | 24 h Rainfall Accumulation (mm) | Peak Flow (m3/s) | Temporal Cv | Spatial Cv |
|---|---|---|---|---|---|---|
| Even 1 | Fuping | 29 July 2007 20:00 to 30 July 2007 20:00 | 63.4 | 29.7 | 0.6011 | 0.3975 |
| Event 2 | Fuping | 30 July 2012 10:00 to 31 July 2012 10:00 | 50.5 | 70.7 | 1.0823 | 0.1927 |
| Event 3 | Fuping | 11 August 2013 07:00 to 12 August 2013 07:00 | 30.9 | 46.6 | 2.3925 | 0.7400 |
| Event 4 | Zijingguan | 21 July 2012 04:00 to 22 July 2012 04:00 | 172.2 | 2580.0 | 1.8865 | 0.6098 |
| Subject | Chosen Option | Subject | Chosen Option |
|---|---|---|---|
| Driving data | GFS each 6 h | WRF output interval | 1 h |
| Integration time step | Dom1: 18 s | domain center | 39°04′15″ N, 113°59′26″ E |
| Dom2: 6 s | Vertical discretization | 40 layers | |
| Horizontal resolution | Dom1: 9 km | Pressure | 50 hPa |
| Dom2: 3 km | Projection resolution | Lambert | |
| Horizontal grid number | Dom1: 140 × 140 | Longwave radiation | RRTM |
| Dom2: 150 × 120 | Shortwave radiation | Dudhia |
| Ensemble Scenarios | Event 1 | Event 2 | Event 3 | Event 4 | |
|---|---|---|---|---|---|
| Microphysics scheme | Lin | ✔ | |||
| WSM6 | ✔ | ✔ | ✔ | ||
| Cumulus convection | KF | ✔ | ✔ | ||
| GD | ✔ | ✔ | |||
| Planetary boundary layer | YSU | ✔ | ✔ | ✔ | |
| MYJ | ✔ | ||||
| Storm Event | Observed | No Data Assimilation | Data Assimilation | Improvement | |||
|---|---|---|---|---|---|---|---|
| Forecasted | RE | Forecasted | RE | Forecasted | RE | ||
| Event 1 | 63.38 | 49.35 | −0.221 | 67.46 | 0.064 | 18.11 | 0.157 |
| Event 2 | 50.48 | 37.22 | −0.263 | 52.18 | 0.034 | 14.96 | 0.229 |
| Event 3 | 30.82 | 19.05 | −0.382 | 29.58 | −0.040 | 10.53 | 0.342 |
| Event 4 | 172.17 | 128.36 | −0.254 | 148.12 | −0.140 | 19.76 | 0.114 |
| Average | 79.21 | 58.49 | −0.280 | 74.34 | −0.020 | 15.85 | 0.260 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Liu, J.; Li, C.; Liu, Y.; Yu, F. Data Assimilation for Rainfall-Runoff Prediction Based on Coupled Atmospheric-Hydrologic Systems with Variable Complexity. Remote Sens. 2021, 13, 595. https://doi.org/10.3390/rs13040595
Wang W, Liu J, Li C, Liu Y, Yu F. Data Assimilation for Rainfall-Runoff Prediction Based on Coupled Atmospheric-Hydrologic Systems with Variable Complexity. Remote Sensing. 2021; 13(4):595. https://doi.org/10.3390/rs13040595
Chicago/Turabian StyleWang, Wei, Jia Liu, Chuanzhe Li, Yuchen Liu, and Fuliang Yu. 2021. "Data Assimilation for Rainfall-Runoff Prediction Based on Coupled Atmospheric-Hydrologic Systems with Variable Complexity" Remote Sensing 13, no. 4: 595. https://doi.org/10.3390/rs13040595
APA StyleWang, W., Liu, J., Li, C., Liu, Y., & Yu, F. (2021). Data Assimilation for Rainfall-Runoff Prediction Based on Coupled Atmospheric-Hydrologic Systems with Variable Complexity. Remote Sensing, 13(4), 595. https://doi.org/10.3390/rs13040595