Three-Dimensional Characterization of a Coastal Mode-Water Eddy from Multiplatform Observations and a Data Reconstruction Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multiplatform and Multivariable Data Approach
2.1.1. Temperature, Salinity, Pressure and Chlorophyll-a from Glider Profiles
2.1.2. Surface Currents from HFR
2.1.3. Vertical Profiles of Potential Density Anomaly and Currents from a Moored Buoy
2.1.4. Chl-a Images and Wind Data
2.1.5. Numerical Simulations
2.2. Method for the 3D Reconstruction of the Observed Fields
2.2.1. The ROOI Method
2.2.2. Implementation of the ROOI Method
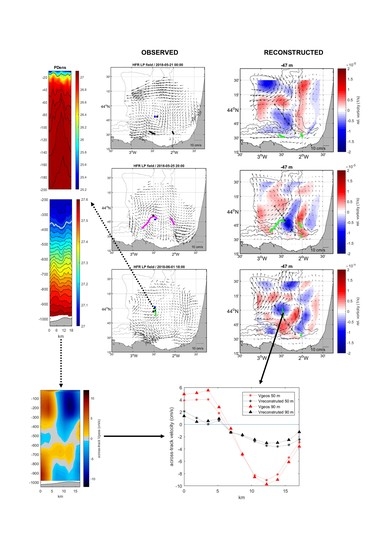
3. Results
3.1. Observed 3D Properties of the Eddy
3.2. Reconstruction of the 3D Eddy Current Velocity Fields
3.2.1. Skill of the Reconstruction
3.2.2. Reconstructed 3D Eddy Current Velocity Fields and Associated Transports
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
- -
- Deep glider: http://www.ifremer.fr/co/ego/ego/v2/comet/comet_20180517/ (accessed on 9 December 2020)
- -
- Shallow glider: http://www.ifremer.fr/co/ego/ego/v2/sebastian/sebastian_20180517/ (accessed on 9 December 2020)
- -
- HFR: https://www.euskoos.eus/en/data/basque-ocean-meteorological-network/high-frequency-coastal-radars/ (accessed on 9 December 2020)
- -
- Mooring: https://www.euskoos.eus/en/data/basque-ocean-meteorological-network/donostia-deep-water-buoy/ (accessed on 9 December 2020)
- -
- Chl-a images: https://resources.marine.copernicus.eu/?option=com_csw&view=details&product_id=OCEANCOLOUR_ATL_CHL_L3_NRT_OBSERVATIONS_009_036 (accessed on 9 December 2020)
- -
- Wind: http://mandeo.meteogalicia.es/thredds/catalogos/DATOS/ARCHIVE/WRF/WRF_hist.html (accessed on 9 December 2020)
- -
- IBI: https://resources.marine.copernicus.eu/?option=com_csw&view=details&product_id=IBI_MULTIYEAR_PHY_005_002 (accessed on 9 December 2020)
Acknowledgments
Conflicts of Interest
References
- Peliz, A.; Santos, A.M.P.; Oliveira, P.B.; Dubert, J. Extreme cross-shelf transport induced by eddy interactions southwest of Iberia in winter 2001. Geophys. Res. Lett. 2004, 31, L08301. [Google Scholar] [CrossRef]
- Shapiro, G.I.; Stanichny, S.V.; Stanychna, R.R. Anatomy of shelf–deep sea exchanges by a mesoscale eddy in the North West Black Sea as derived from remotely sensed data. Remote Sens. Environ. 2010, 114, 867–875. [Google Scholar] [CrossRef]
- Combes, V.; Chenillat, F.; Di Lorenzo, E.; Rivière, P.; Ohman, M.; Bograd, S. Cross-shore transport variability in the California Current: Ekman upwelling vs. eddy dynamics. Prog. Oceanogr. 2013, 109, 78–89. [Google Scholar] [CrossRef]
- Cherian, D.A.; Brink, K. Offshore transport of shelf water by deep-ocean eddies. J. Phys. Oceanogr. 2016, 46, 3599–3621. [Google Scholar] [CrossRef] [Green Version]
- Rubio, A.; Caballero, A.; Orfila, A.; Hernández-Carrasco, I.; Ferrer, L.; González, M.; Solabarrieta, L.; Mader, J. Eddy-induced cross-shelf export of high Chl-a coastal waters in the SE Bay of Biscay. Remote Sens. Environ. 2018, 205, 290–304. [Google Scholar] [CrossRef] [Green Version]
- Akpınar, A.; Charria, G.; Theetten, S.; Vandermeirsch, F. Cross-shelf exchanges in the northern Bay of Biscay. J. Marine Syst. 2020, 205, 103314. [Google Scholar] [CrossRef]
- Brzezinski, M.A.; Washburn, L. Phytoplankton primary productivity in the Santa Barbara Channel: Effects of wind-driven upwelling and mesoscale eddies. J. Geophys. Res. Oceans 2011, 116, C12013. [Google Scholar] [CrossRef] [Green Version]
- Moore, T.S., II; Matear, R.J.; Marra, J.; Clementson, L. Phytoplankton variability off the Western Australian Coast: Mesoscale eddies and their role in cross-shelf exchange. Deep-Sea Res. Pt. II 2007, 54, 943–960. [Google Scholar] [CrossRef]
- Campbell, R.; Diaz, F.; Hu, Z.; Doglioli, A.; Petrenko, A.; Dekeyser, I. Nutrients and plankton spatial distributions induced by a coastal eddy in the Gulf of Lion. Insights from a numerical model. Prog. Oceanogr. 2013, 109, 47–69. [Google Scholar] [CrossRef]
- Huthnance, J.M.; Holt, J.T.; Wakelin, S.L. Deep ocean exchange with west-European shelf seas. Ocean Sci. 2009, 5, 621–634. [Google Scholar] [CrossRef] [Green Version]
- Mizobata, K.; Wang, J.; Saitoh, S.i. Eddy-induced cross-slope exchange maintaining summer high productivity of the Bering Sea shelf break. J. Geophys. Res. Oceans 2006, 111, C10. [Google Scholar] [CrossRef] [Green Version]
- Dietze, H.; Matear, R.; Moore, T. Nutrient supply to anticyclonic meso-scale eddies off western Australia estimated with artificial tracers released in a circulation model. Deep-Sea Res. Pt. I 2009, 56, 1440–1448. [Google Scholar] [CrossRef]
- Le Cann, B.; Serpette, A. Intense warm and saline upper ocean inflow in the southern Bay of Biscay in autumn–winter 2006–2007. Cont. Shelf Res. 2009, 29, 1014–1025. [Google Scholar] [CrossRef]
- Charria, G.; Lazure, P.; Le Cann, B.; Serpette, A.; Reverdin, G.; Louazel, S.; Batifoulier, F.; Dumas, F.; Pichon, A.; Morel, Y. Surface layer circulation derived from Lagrangian drifters in the Bay of Biscay. J. Marine Syst. 2013, 109, S60–S76. [Google Scholar] [CrossRef]
- Solabarrieta, L.; Rubio, A.; Castanedo, S.; Medina, R.; Charria, G.; Hernández, C. Surface water circulation patterns in the southeastern Bay of Biscay: New evidences from HF radar data. Cont. Shelf Res. 2014, 74, 60–76. [Google Scholar] [CrossRef] [Green Version]
- Pingree, R.; Le Cann, B. Three anticyclonic Slope Water Oceanic eDDIES (SWODDIES) in the southern Bay of Biscay in 1990. Deep Sea Res. 1992, 39, 1147–1175. [Google Scholar] [CrossRef]
- Caballero, A.; Pascual, A.; Dibarboure, G.; Espino, M. Sea level and Eddy Kinetic Energy variability in the Bay of Biscay, inferred from satellite altimeter data. J. Marine Syst. 2008, 72, 116–134. [Google Scholar] [CrossRef]
- Caballero, A.; Ferrer, L.; Rubio, A.; Charria, G.; Taylor, B.H.; Grima, N. Monitoring of a quasi-stationary eddy in the Bay of Biscay by means of satellite, in situ and model results. Deep-Sea Res. Pt. II 2014, 106, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Caballero, A.; Rubio, A.; Ruiz, S.; Le Cann, B.; Testor, P.; Mader, J.; Hernández, C. South-Eastern Bay of Biscay eddy-induced anomalies and their effect on chlorophyll distribution. J. Marine Syst. 2016, 162, 57–72. [Google Scholar] [CrossRef] [Green Version]
- McGillicuddy, D.J.; Johnson, R.; Siegel, D.; Michaels, A.; Bates, N.; Knap, A. Mesoscale variations of biogeochemical properties in the Sargasso Sea. J. Geophys. Res. Oceans 1999, 104, 13381–13394. [Google Scholar] [CrossRef] [Green Version]
- Manso-Narvarte, I.; Fredj, E.; Jordà, G.; Berta, M.; Griffa, A.; Caballero, A.; Rubio, A. 3D reconstruction of ocean velocity from high-frequency radar and acoustic Doppler current profiler: A model-based assessment study. Ocean Sci. 2020, 16, 575–591. [Google Scholar] [CrossRef]
- Mantovani, C.; Corgnati, L.; Horstmann, J.; Rubio, A.; Reyes, E.; Quentin, C.; Cosoli, S.; Asensio, J.L.; Mader, J.; Griffa, A. Best practices on High Frequency Radar deployment and operation for ocean current measurement. Front. Mar. Sci. 2020, 7, 210. [Google Scholar] [CrossRef] [Green Version]
- Solabarrieta, L.; Rubio, A.; Cárdenas, M.; Castanedo, S.; Esnaola, G.; Méndez, F.J.; Medina, R.; Ferrer, L. Probabilistic relationships between wind and surface water circulation patterns in the SE Bay of Biscay. Ocean Dynam. 2015, 65, 1289–1303. [Google Scholar] [CrossRef]
- Solabarrieta, L.; Frolov, S.; Cook, M.; Paduan, J.; Rubio, A.; González, M.; Mader, J.; Charria, G. Skill assessment of hf radar–derived products for lagrangian simulations in the bay of biscay. J. Atmos. Ocean. Tech. 2016, 33, 2585–2597. [Google Scholar] [CrossRef] [Green Version]
- Rubio, A.; Reverdin, G.; Fontán, A.; González, M.; Mader, J. Mapping near-inertial variability in the SE Bay of Biscay from HF radar data and two offshore moored buoys. Geophys. Res. Lett. 2011, 38, 19. [Google Scholar] [CrossRef]
- Bender, L.; DiMarco, S. Quality Control Analysis of Acoustic Doppler Current Profiler Data Collected on Offshore Platforms of the Gulf of Mexico; OCS Study MMS 2009-010; U.S. Dept. of the Interior, Minerals Mgmt. Service, Gulf of Mexico OCS Region: New Orleans, LA, USA, 2009; 63p. [Google Scholar]
- Ferrer, L.; Fontán, A.; Mader, J.; Chust, G.; González, M.; Valencia, V.; Uriarte, A.; Collins, M. Low-salinity plumes in the oceanic region of the Basque Country. Cont. Shelf Res. 2009, 29, 970–984. [Google Scholar] [CrossRef]
- Rubio, A.; Fontán, A.; Lazure, P.; González, M.; Valencia, V.; Ferrer, L.; Mader, J.; Hernández, C. Seasonal to tidal variability of currents and temperature in waters of the continental slope, southeastern Bay of Biscay. J. Marine Syst. 2013, 109, S121–S133. [Google Scholar] [CrossRef]
- Ferrer, L.; Liria, P.; Bolaños, R.; Balseiro, C.; Carracedo, P.; González-Marco, D.; González, M.; Fontán, A.; Mader, J.; Hernández, C. Reliability of coupled meteorological and wave models to estimate wave energy resource in the Bay of Biscay. In Proceedings of the 3rd International Conference on Ocean Energy (ICOE), Bilbao, Spain, 6–8 October 2010; p. 6. [Google Scholar]
- Sotillo, M.; Cailleau, S.; Lorente, P.; Levier, B.; Aznar, R.; Reffray, G.; Amo-Baladrón, A.; Chanut, J.; Benkiran, M.; Alvarez-Fanjul, E. The MyOcean IBI Ocean Forecast and Reanalysis Systems: Operational products and roadmap to the future Copernicus Service. J. Oper. Oceanogr. 2015, 8, 63–79. [Google Scholar] [CrossRef]
- Fredj, E.; Roarty, H.; Kohut, J.; Smith, M.; Glenn, S. Gap filling of the coastal ocean surface currents from HFR data: Application to the Mid-Atlantic Bight HFR Network. J. Atmos. Ocean. Tech. 2016, 33, 1097–1111. [Google Scholar] [CrossRef]
- Kaplan, A.; Kushnir, Y.; Cane, M.A.; Blumenthal, M.B. Reduced space optimal analysis for historical data sets: 136 years of Atlantic sea surface temperatures. J. Geophys. Res. Oceans 1997, 102, 27835–27860. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, A.; Kushnir, Y.; Cane, M.A. Reduced space optimal interpolation of historical marine sea level pressure: 1854–1992. J. Climate 2000, 13, 2987–3002. [Google Scholar] [CrossRef] [Green Version]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33, 1. [Google Scholar] [CrossRef]
- Jordà, G.; Sánchez-Román, A.; Gomis, D. Reconstruction of transports through the Strait of Gibraltar from limited observations. Clim. Dynam. 2016, 48, 851–865. [Google Scholar] [CrossRef]
- Zhao, M.; Timmermans, M.L. Vertical scales and dynamics of eddies in the Arctic Ocean’s Canada Basin. J. Geophys. Res. Oceans 2015, 120, 8195–8209. [Google Scholar] [CrossRef]
- Carpenter, J.; Timmermans, M.L. Deep mesoscale eddies in the Canada Basin, Arctic Ocean. Geophys. Res. Lett. 2012, 39, 20. [Google Scholar] [CrossRef] [Green Version]
- Manso-Narvarte, I.; Caballero, A.; Rubio, A.; Dufau, C.; Birol, F. Joint analysis of coastal altimetry and high-frequency (HF) radar data: Observability of seasonal and mesoscale ocean dynamics in the Bay of Biscay. Ocean Sci. 2018, 14, 1265–1281. [Google Scholar] [CrossRef] [Green Version]
- McGillicuddy, D.J. Formation of intrathermocline lenses by eddy–wind interaction. J. Phys. Oceanogr. 2015, 45, 606–612. [Google Scholar] [CrossRef] [Green Version]
- McGillicuddy, D.J.; Anderson, L.A.; Bates, N.R.; Bibby, T.; Buesseler, K.O.; Carlson, C.A.; Davis, C.S.; Ewart, C.; Falkowski, P.G.; Goldthwait, S.A. Eddy/wind interactions stimulate extraordinary mid-ocean plankton blooms. Science 2007, 316, 1021–1026. [Google Scholar] [CrossRef] [PubMed]
- Teles-Machado, A.; Peliz, Á.; McWilliams, J.C.; Dubert, J.; Le Cann, B. Circulation on the northwestern Iberian margin: Swoddies. Prog. Oceanogr. 2016, 140, 116–133. [Google Scholar] [CrossRef] [Green Version]
- Irigoien, X.; Fiksen, Ø.; Cotano, U.; Uriarte, A.; Alvarez, P.; Arrizabalaga, H.; Boyra, G.; Santos, M.; Sagarminaga, Y.; Otheguy, P. Could Biscay Bay Anchovy recruit through a spatial loophole? Prog. Oceanogr. 2007, 74, 132–148. [Google Scholar] [CrossRef]








| Observing Platforms/ Dataset | Purpose | Variable | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| Glider | Eddy analysis | . Salinity, , Chl-a, Vgeos | 3D grid z: 1m x, y: uneven | Uneven |
| Reconstruction | Uneven (24 h LP) | |||
| Validation | Vgeos | Uneven | ||
| HFR | Eddy analysis | U, V | 2D grid x, y: 5 km | Daily + Hourly (10d LP) |
| Reconstruction | Average | |||
| Mooring | Reconstruction | U, V, | 1D profile z: 8 m (uneven for | Average |
| Sentinel-3A (satellite) | Eddy analysis | Chl-a | 2D grid x, y: 1 km | Daily |
| WRF (model) | Eddy analysis | Wind U, V | Pointwise | Hourly |
| IBI (model) | Reconstruction | U, V, | 3D grid x, y: 0.083° z: uneven | Daily |
| From | To | |
|---|---|---|
| P1 | 17:00 20 May | 17:00 21 May |
| P2 | 00:00 25 May | 23:59 26 May |
| P3 | 02:37 2 June | 02:06 3 June |
| UHFR | VHFR | UADCP | VADCP | |
|---|---|---|---|---|
| P1 | 1.39 | 1.37 | 0.58 | 0.68 |
| P2 | 1.33 | 1.18 | 1.74 | 0.58 |
| P3 | 1.72 | 1.74 | 1.35 | 0.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manso-Narvarte, I.; Rubio, A.; Jordà, G.; Carpenter, J.; Merckelbach, L.; Caballero, A. Three-Dimensional Characterization of a Coastal Mode-Water Eddy from Multiplatform Observations and a Data Reconstruction Method. Remote Sens. 2021, 13, 674. https://doi.org/10.3390/rs13040674
Manso-Narvarte I, Rubio A, Jordà G, Carpenter J, Merckelbach L, Caballero A. Three-Dimensional Characterization of a Coastal Mode-Water Eddy from Multiplatform Observations and a Data Reconstruction Method. Remote Sensing. 2021; 13(4):674. https://doi.org/10.3390/rs13040674
Chicago/Turabian StyleManso-Narvarte, Ivan, Anna Rubio, Gabriel Jordà, Jeffrey Carpenter, Lucas Merckelbach, and Ainhoa Caballero. 2021. "Three-Dimensional Characterization of a Coastal Mode-Water Eddy from Multiplatform Observations and a Data Reconstruction Method" Remote Sensing 13, no. 4: 674. https://doi.org/10.3390/rs13040674
APA StyleManso-Narvarte, I., Rubio, A., Jordà, G., Carpenter, J., Merckelbach, L., & Caballero, A. (2021). Three-Dimensional Characterization of a Coastal Mode-Water Eddy from Multiplatform Observations and a Data Reconstruction Method. Remote Sensing, 13(4), 674. https://doi.org/10.3390/rs13040674