Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar
Abstract
:1. Introduction
2. GNSS-Based Bistatic Radar System Geometry Signal Model
3. The Clutter Cancellation and Proposed Long Time Integration Algorithm
3.1. The Principle of Extensive Cancellation Algorithm
3.2. The Proposed Long Time Integration Algorithm
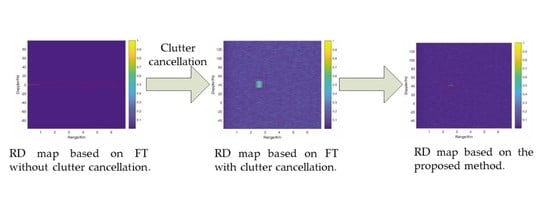
4. Simulation Results and Discussion
4.1. Simulation Results
4.1.1. Detection Results of Target with Smooth Motion
4.1.2. Detection Results of Target with Constant Acceleration
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | global navigation satellite system |
| ECA | extensive cancellation algorithm |
| LIFT | long-time integration Fourier transform |
| RA | relative acceleration |
| PBR | passive bistatic radar |
| LMS | least mean square |
| NLMS | normalized least mean square |
| RLS | recursive least square |
| LS | least square |
| EIRP | effective isotropic radiated power |
| CPI | coherent processing interval |
| FrFT | fractional Fourier transform |
| SNR | signal to noise ratio |
| DC | Doppler centroid |
| DMR | Doppler modulated rate |
| FT | Fourier transform |
| EIR | energy integration ratio |
| RD | range Doppler |
References
- Zeng, H.; Chen, J.; Wang, P.; Liu, W.; Zhou, X.; Yang, W. Moving Target Detection in Multi-Static GNSS-Based Passive Radar Based on Multi-Bernoulli Filter. Remote Sens. 2020, 12, 3495. [Google Scholar]
- He, Z.-Y.; Yang, Y.; Chen, W.; Weng, D.-J. Moving Target Imaging Using GNSS-Based Passive Bistatic Synthetic Aperture Radar. Remote Sens. 2020, 12, 3356. [Google Scholar]
- Hu, C.; Liu, C.; Wang, R.; Chen, L.; Wang, L. Detection and SISAR Imaging of Aircrafts Using GNSS Forward Scatter Radar: Signal Modeling and Experimental Validation. IEEE Trans. Aerosp. Electr. Syst. 2017, 53, 2077–2093. [Google Scholar]
- Noviello, C.; Esposito, G.; Fasano, G.; Renga, A.; Soldovieri, F.; Catapano, I. Small-UAV Radar Imaging System Performance with GPS and CDGPS Based Motion Compensation. Remote Sens. 2020, 12, 3463. [Google Scholar]
- Wang, Y.; Bao, Q.; Wang, D.; Chen, Z. An Experimental Study of Passive Bistatic Radar Using Uncooperative Radar as a Transmitter. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1868–1872. [Google Scholar]
- Zeng, H.; Wang, P.; Chen, J.; Liu, W.; Ge, L. A Novel General Imaging Formation Algorithm for GNSS-Based Bistatic SAR. Sensors 2016, 16, 1–15. [Google Scholar]
- Colone, F.; Bongioanni, C.; Lombardo, P. Multifrequency integration in FM radio-based passive bistatic radar. Part I: Target detection. IEEE Aerosp. Electr. Syst. Mag. 2013, 28, 28–39. [Google Scholar]
- Malanowski, M.; Kulpa, K.; Kulpa, J.; Samczynski, P.; Misiurewicz, J. Analysis of detection range of FM-based passive radar. IET Radar Sonar Navig. 2014, 8, 153–159. [Google Scholar]
- Howland, P.; Maksimiuk, D.E.; Reitsma, G. FM radio based bistatic radar. Proc.-Radar Sonar Navig. 2005, 152, 107–115. [Google Scholar]
- Martelli, T.; Colone, F.; Tilli, E.; di Lallo, A. Multi-frequency target detection techniques for DVB-T based passive radars sensors. Sensors 2016, 10, 1594. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, H.D.; Long, N.R.W. Television-based Bistatic Radar. IEE Proc. F Commun. Radar Signal Process. 1986, 133, 649–657. [Google Scholar]
- Guo, H.; Woodbridge, K.; Baker, C.J. Evaluation of WIFI Beacon Transmissions for Wireless Based Passive R adar. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Colone, F.; Falcone, P.; Bongioanni, C.; Long, P.L. WiFi-based passive bistatic radar: Data processing schemes and experimental results. IEEE Trans. Aerosp. Electr. Syst. 2012, 48, 1061–1079. [Google Scholar]
- Zemmari, R.; Broetje, M.; Battistello, G.; Nickel, U. GSM passive coherent location system: Performance prediction and measurement evaluation. IET Radar Sonar Navig. 2014, 8, 94–105. [Google Scholar]
- Ma, H.; Antoniou, M.; Pastina, D.; Santi, F.; Pieralice, F.; Bucciarelli, M.; Cherniakov, M. Maritime moving target indication using passive GNSS-based bistatic radar. IEEE Trans. Aerosp. Electr. Syst. 2018, 54, 115–130. [Google Scholar]
- Hui, M.; Michail, A.; Stove, A.G.; Winkel, J.; Cherniakov, M. Maritime Moving Target Localization Using Passive GNSS-Based Multistatic Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4808–4819. [Google Scholar]
- Pastina, D.; Santi, F.; Pieralice, F.; Bucciarelli, M.; Ma, H.; Tzagkas, D.; Antoniou, M.N.; Cherniakov, M. Maritime moving target long time integration for GNSS-based passive bistatic radar. IEEE Trans. Aerosp. Electr. Syst. 2018, 6, 1–12. [Google Scholar]
- Tan, D.K.P.; Lesturgie, M.; Sun, H.; Lu, Y. Space time interference analysis and suppression for airborne passive radar using transmissions of opportunity. IET Radar Sonar Navig. 2014, 8, 142–152. [Google Scholar]
- Ma, Y.; Shan, T.; Zhang, Y.D.; Amin, M.G.; Tao, R.; Feng, Y. A novel two-dimensional sparse-weight NLMS filtering scheme for passive bistatic radar. IEEE Geosci. Remote Sens. Lett. 2016, 13, 676–680. [Google Scholar]
- Zhu, X.-L.; Zhang, X.-D. Adaptive RLS algorithm for blind source separation using a natural gradient. IEEE Signal Process. Lett. 2002, 9, 432–435. [Google Scholar]
- Colone, F.; O’Hagan, D.W.; Lombardo, P.; Baker, C.J. A Multistage Processing Algorithm for Disturbance Removal and Target Detection in Passive Bistatic Radar. IEEE Trans. Aerosp. Electr. Syst. 2009, 45, 698–722. [Google Scholar]
- Colone, F.; Palmarini, C.; Martelli, T.; Tilli, E. Sliding extensive cancellation algorithm for disturbance removal in passive radar. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1309–1326. [Google Scholar]
- Zhao, Z.; Zhou, X.; Zhu, S.; Hong, S. Reduced complexity multipath clutter rejection approach for DRM-based HF passive bistatic radar. IEEE Access 2017, 5, 20228–20234. [Google Scholar]
- Rohman, P.A.; Nishimoto, M. Ground clutter suppression in GPR using framing based mean removal and subspace decomposition. In Proceedings of the 2017 International Symposium on Antennas and Propagation (ISAP), Phuket, Thailand, 30 October–2 November 2017; pp. 1–2. [Google Scholar]
- Cardillo, E.; Li, C.; Caddemi, A. Vital Sign Detection and Radar Self-Motion Cancellation Through Clutter Identification. IEEE Trans. Microw. Theory Tech. 2021. [Google Scholar] [CrossRef]
- Zeng, H.-C.; Chen, J.; Wang, P.-B.; Yang, W.; Liu, W. 2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-Based Passive Radar. Remote Sens. 2018, 99, 1164. [Google Scholar]
- Tao, R.; Deng, B.; Wang, Y. Research progress of the fractional Fourier transform in signal processing. Sci. China Inf. Sci. 2006, 49, 1–25. [Google Scholar]
- Xu, J.; Yan, L.; Zhou, X.; Long, T.; Xia, X.-G.; Wang, Y.-L.; Farina, A.; Xai, X.-G. Adaptive Radon-Fourier Transform for Weak Radar Target Detection. IEEE Trans. Aerosp. Electr. Syst. 2018, 99, 686–697. [Google Scholar]
- He, Z.; Yang, Y.; Chen, W. A Hybrid integration method for moving target detection with GNSS-based passive radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 99, 1. [Google Scholar]
- Li, Z.; Santi, F.; Pastina, D.; Lombardo, P. Passive Radar Array with Low-Power Satellite Illuminators Based on Fractional Fourier Transform. IEEE Sens. J. 2017, 17, 8378–8394. [Google Scholar]
- Zhou, X.; Wang, P.; Chen, J.; Men, Z.; Liu, W.; Zeng, H.A. Modified Radon Fourier Transform for GNSS-Based Bistatic Radar Target Detection. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s distribution: Principle, implementation, properties, and performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Coherent Integration for Maneuvering Target Detection Based on Radon-Lv’s Distribution. IEEE Signal Process. Lett. 2015, 22, 1467–1471. [Google Scholar]















| Parameter | Setting Value | Parameter | Setting Value |
|---|---|---|---|
| Carrier frequency | 1575.42 MHz | Bandwidth | 1.023 MHz |
| Complex sampling rate | 4.092 MHz | Pulse repeat frequency | 1000 Hz |
| Pulse number | 3000 | Range resolution | 146.6 m |
| Parameter | SNR (dB) | Sample Delay |
|---|---|---|
| Direct signal | 0 | 0 |
| Multipath 1 | −7.96 | 5 |
| Multipath 2 | −6.02 | 9 |
| Target echo | −40 | 33 |
| Parameter | Symbol | Setting Value |
|---|---|---|
| Power density | −158 dBw | |
| Wavelength | 0.19 m | |
| Code duration | 1 ms | |
| Code bandwidth | 1.023 MHz | |
| Receiver antenna gain | 35 dB | |
| RCS | 20 dB | |
| Noise power | −143 dB | |
| System loss factor | 0.5 | |
| Coherent time | 3 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Cha, H.; Zhou, Z.; Tian, B. Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar. Remote Sens. 2021, 13, 701. https://doi.org/10.3390/rs13040701
Wang B, Cha H, Zhou Z, Tian B. Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar. Remote Sensing. 2021; 13(4):701. https://doi.org/10.3390/rs13040701
Chicago/Turabian StyleWang, Binbin, Hao Cha, Zibo Zhou, and Bin Tian. 2021. "Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar" Remote Sensing 13, no. 4: 701. https://doi.org/10.3390/rs13040701
APA StyleWang, B., Cha, H., Zhou, Z., & Tian, B. (2021). Clutter Cancellation and Long Time Integration for GNSS-Based Passive Bistatic Radar. Remote Sensing, 13(4), 701. https://doi.org/10.3390/rs13040701