GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data
Abstract
:1. Introduction
2. Basis of the Model for Above-Ground Biomass (AGB) and Crop Yield Estimation
2.1. Remote Sensing of Active Photosynthetic Radiation (APAR)
2.2. Calculations of Yield Stressors
2.2.1. Vapor Stress (VS)
2.2.2. Plant Temperature Constraint (TS)
2.2.3. Soil Moisture Stress (SMS)
2.2.4. Daily Actual ET Modeling Scheme
2.2.5. Soil Water Properties
2.2.6. Total Soil Moisture Content ()
2.2.7. A First Estimate of the Root Zone Soil Moisture ()
2.2.8. Soil Moisture Stress Trigger ) and a First Estimate of Moisture Stress Biomass ()
2.2.9. Splitting the ET into Evaporation and Transpiration
3. Data and Analyses
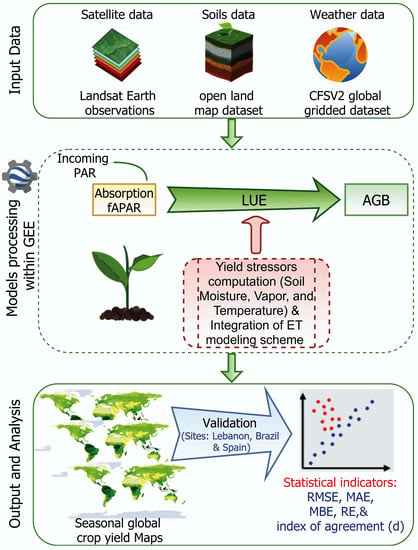
3.1. Model Overview
3.2. Study Sites and Field Data
3.2.1. Skaff (Bekaa, Lebanon) Site
3.2.2. AREC (Bekaa, Lebanon) Site
3.2.3. São Desidério (Brazil) Site
3.2.4. Albacete (Spain) Site
3.3. Datasets
3.3.1. Landsat Surface Reflectance Data
3.3.2. Weather Data
3.4. Definition of the Growing Season
3.5. Statistical Indicators
4. Results and Discussion
4.1. Model Performance
4.2. Within-Field Spatial Variability in Above-Ground Biomass (AGB), Soil Moisture Stress (SMS), and Crop Yield
4.2.1. Potato: Skaff (Bekaa, Lebanon) Site
4.2.2. Corn: São Desidério (Brazil) Site
4.2.3. Wheat: Albacete (Spain) Site
4.3. Seasonal Co-Variability in Above-Ground Dry Biomass (AGDB), Environmental Stressors, and Yield: Examples from Lebanon
4.4. Assessment of the Operational Model: Strengths and Weaknesses
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khaki, S.; Wang, L. Crop yield prediction using deep neural networks. Front. Plant Sci. 2019, 10, 621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef] [Green Version]
- Scharf, P.C.; Lory, J.A. Calibrating corn color from aerial photographs to predict sidedress nitrogen need. Agron. J. 2002, 94, 397–404. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Mahlein, A.K.; Oerke, E.-C.; Steiner, U.; Dehne, H.W. Recent advances in sensing plant diseases for precision crop protection. Eur. J. Plant Pathol. 2012, 133, 197–209. [Google Scholar] [CrossRef]
- Dorward, A.; Chirwa, E. A Review of Methods for Estimating Yield and Production Impacts. 2010. Available online: https://eprints.soas.ac.uk/16731/1/FISP%20Production%20Methodologies%20review%20Dec%20Final.pdf (accessed on 19 February 2021).
- Rauff, K.O.; Bello, R. A review of crop growth simulation models as tools for agricultural meteorology. Agric. Sci. 2015, 6, 1098. [Google Scholar] [CrossRef]
- Tiwari, P.; Shukla, P.K. A Review on Various Features and Techniques of Crop Yield Prediction Using Geo-Spatial Data. Int. J. Organ. Collect. Intell. (IJOCI) 2019, 9, 37–50. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Yitayew, M.; Slack, D.C.; Hutchinson, C.F.; Huete, A.; Petersen, M.S. Estimating crop yields and production by integrating the FAO Crop Specific Water Balance model with real-time satellite data and ground-based ancillary data. Int. J. Remote Sens. 2000, 21, 3487–3508. [Google Scholar] [CrossRef]
- Khan, A.; Stöckle, C.O.; Nelson, R.L.; Peters, T.; Adam, J.C.; Lamb, B.; Chi, J.; Waldo, S. Estimating Biomass and Yield Using METRIC Evapotranspiration and Simple Growth Algorithms. Agron. J. 2019, 111, 536–544. [Google Scholar] [CrossRef] [Green Version]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.J.; Rötter, R.P.; Cammarano, D.; et al. Uncertainty in simulating wheat yields under climate change. Nat. Clim. Chang. 2013, 3, 827. [Google Scholar] [CrossRef] [Green Version]
- Hoogenboom, G. Contribution of agrometeorology to the simulation of crop production and its applications. Agric. For. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- Steduto, P.; Albrizio, R. Resource use efficiency of field-grown sunflower, sorghum, wheat and chickpea: II. Water use efficiency and comparison with radiation use efficiency. Agric. For. Meteorol. 2005, 130, 269–281. [Google Scholar] [CrossRef]
- Jones, C.A. CERES-Maize: A Simulation Model of Maize Growth and Development; Texas A&M University Press: College Station, TX, USA, 1986. [Google Scholar]
- Williams, J.R.; Jones, C.A.; Dyke, P.T. The EPIC model and its application. In Proceedings of the International Symposium on Minimum Data Sets for Agrotechnology Transfer, Patancheru, India, 21–26 March 1983; pp. 111–121. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Steduto, P.; Raes, D.; Hsiao, T.C.; Fereres, E.; Heng, L.K.; Howell, T.A.; Evett, S.R.; Rojas-Lara, B.A.; Farahani, H.J.; Izzi, G.; et al. Concepts and applications of AquaCrop: The FAO crop water productivity model. In Crop Modeling and Decision Support; Springer: Berlin, Germany, 2009; pp. 175–191. [Google Scholar]
- Stockle, C.O.; Martin, S.A.; Campbell, G.S. CropSyst, a cropping systems simulation model: Water/nitrogen budgets and crop yield. Agric. Syst. 1994, 46, 335–359. [Google Scholar] [CrossRef]
- Boote, K.J.; Jones, J.W.; Pickering, N.B. Potential uses and limitations of crop models. Agron. J. 1996, 88, 704–716. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Ines, A.V.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Maas, S. Using satellite data to improve model estimates of crop yield. Agron. J. 1988, 80, 655–662. [Google Scholar] [CrossRef]
- Sibley, A.M.; Grassini, P.; Thomas, N.E.; Cassman, K.G.; Lobell, D.B. Testing remote sensing approaches for assessing yield variability among maize fields. Agron. J. 2014, 106, 24–32. [Google Scholar] [CrossRef]
- Groten, S. NDVI—Crop monitoring and early yield assessment of Burkina Faso. Remote Sens. 1993, 14, 1495–1515. [Google Scholar] [CrossRef]
- Sharma, T.; Sudha, K.; Ravi, N.; Navalgund, R.; Tomar, K.; Chakravarty, N.; Das, D. Procedures for wheat yield prediction using Landsat MSS and IRS-1 A data. Int. J. Remote Sens. 1993, 14, 2509–2518. [Google Scholar] [CrossRef]
- Monteith, J. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef] [Green Version]
- Daughtry, C.; Gallo, K.; Goward, S.; Prince, S.; Kustas, W. Spectral estimates of absorbed radiation and phytomass production in corn and soybean canopies. Remote Sens. Environ. 1992, 39, 141–152. [Google Scholar] [CrossRef]
- Kumar, M. Remote Sensing of Crop Growth. In Plants and the Daylight Spectrum: Proceedings of the First International Symposium of the British Photobiology Society, Leicester, UK, 5–8 January 1981; Smith, H., Ed.; Academic Press: Cambridge, MA, USA, 1981; Volume 1, pp. 133–144. [Google Scholar]
- Boschetti, M.; Stroppiana, D.; Confalonieri, R.; Brivio, P.A.; Crema, A.; Bocchi, S. Estimation of rice production at regional scale with a Light Use Efficiency model and MODIS time series. Ital. J. Remote Sens. Riv. Ital. Di Telerilevamento 2011, 43, 63–81. [Google Scholar] [CrossRef]
- Patel, N.; Bhattacharjee, B.; Mohammed, A.; Tanupriya, B.; Saha, S. Remote sensing of regional yield assessment of wheat in Haryana, India. Int. J. Remote Sens. 2006, 27, 4071–4090. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Ali, S. A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
- Pan, G.; Sun, G.-J.; Li, F.-M. Using QuickBird imagery and a production efficiency model to improve crop yield estimation in the semi-arid hilly Loess Plateau, China. Environ. Model. Softw. 2009, 24, 510–516. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.; Arkebauer, T.J.; Suyker, A.E.; Gonçalves, I.Z. Water productivity and crop yield: A simplified remote sensing driven operational approach. Agric. For. Meteorol. 2018, 249, 501–511. [Google Scholar] [CrossRef]
- Tawk, S.T.; Chedid, M.; Chalak, A.; Karam, S.; Hamadeh, S.K. Challenges and Sustainability of Wheat Production in a Levantine Breadbasket. J. Agric. Food Syst. Community Dev. 2019, 8, 193–209. [Google Scholar] [CrossRef]
- Jaafar, H.; King-Okumu, C.; Haj-Hassan, M.; Abdallah, C.; El-Korek, N.; Ahmad, F. Water Resources within the Upper Orontes and Litani Basins; International Institute for Environment and Development: London, UK, 2016. [Google Scholar]
- Ministry of Agriculture. Recensement Generale. In FAO/Project Recensement Agricole; Lebanese Ministry of Agriculture: Bir Hasan, Lebanon, 2012. [Google Scholar]
- Darwish, T.; Fadel, A.; Baydoun, S.; Jomaa, I.; Awad, M.; Hammoud, Z.; Halablab, O.; Atallah, T. Potato Performance under Different Potassium Levels and Deficit Irrigation in Dry Sub-Humid Mediterranean Conditions; International Potash Institute (IPI): Zug, Switzerland, 2015; pp. 14–35. [Google Scholar]
- AIBA. Agricultural Yearbook of Western Bahia Region—Crop 2016/2017; Barreiras, Brazil, 2017. Available online: http://aiba.org.br/wp-content/uploads/2018/06/anuario-16-17.pdf (accessed on 25 November 2020).
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
- De Oliveira Ferreira Silva, C.; Lilla Manzione, R.; Albuquerque Filho, J.L. Large-Scale Spatial Modeling of Crop Coefficient and Biomass Production in Agroecosystems in Southeast Brazil. Horticulturae 2018, 4, 44. [Google Scholar] [CrossRef] [Green Version]
- Casanova, D.; Epema, G.; Goudriaan, J. Monitoring rice reflectance at field level for estimating biomass and LAI. Field Crop. Res. 1998, 55, 83–92. [Google Scholar] [CrossRef]
- Christensen, S.; Goudriaan, J. Deriving light interception and biomass from spectral reflectance ratio. Remote Sens. Environ. 1993, 43, 87–95. [Google Scholar] [CrossRef]
- Garcia, R.; Kanemasu, E.T.; Blad, B.L.; Bauer, A.; Hatfield, J.L.; Major, D.J.; Reginato, R.J.; Hubbard, K.G. Interception and use efficiency of light in winter wheat under different nitrogen regimes. Agric. For. Meteorol. 1988, 44, 175–186. [Google Scholar] [CrossRef]
- Rochette, P.; Desjardins, R.L.; Pattey, E.; Lessard, R. Crop net carbon dioxide exchange rate and radiation use efficiency in soybean. Agron. J. 1995, 87, 22–28. [Google Scholar] [CrossRef]
- Richards, R.; Townley-Smith, T. Variation in leaf area development and its effect on water use, yield and harvest index of droughted wheat. Aust. J. Agric. Res. 1987, 38, 983–992. [Google Scholar] [CrossRef]
- Varlet-Grancher, C.B.; Bonhomme, R.; Chartier, M.; Artis, P. Efficience de la conversion de l’énergie solaire par un couvert végétal. Acta Oecologica Oecologia Plantarum 1982, 3, 3–26. [Google Scholar]
- Das, D.; Mishra, K.; Kalra, N. Assessing growth and yield of wheat using remotely-sensed canopy temperature and spectral indices. Int. J. Remote Sens. 1993, 14, 3081–3092. [Google Scholar] [CrossRef]
- Calera, A.; González-Piqueras, J.; Melia, J. Monitoring barley and corn growth from remote sensing data at field scale. Int. J. Remote Sens. 2004, 25, 97–109. [Google Scholar] [CrossRef]
- Hatfield, J.; Asrar, G.; Kanemasu, E.T. Intercepted photosynthetically active radiation estimated by spectral reflectance. Remote Sens. Environ. 1984, 14, 65–75. [Google Scholar] [CrossRef]
- Asrar, G.; Myneni, R.; Choudhury, B. Spatial heterogeneity in vegetation canopies and remote sensing of absorbed photosynthetically active radiation: A modeling study. Remote Sens. Environ. 1992, 41, 85–103. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Gao, Z.; Xie, X.; Gao, W.; Chang, N.-B. Spatial analysis of terrain-impacted Photosynthetic Active Radiation (PAR) using MODIS data. GIScience Remote Sens. 2011, 48, 501–521. [Google Scholar] [CrossRef]
- McCree, K.J. Photosynthetically active radiation. In Physiological Plant Ecology I; Springer: Berlin, Germany, 1981; pp. 41–55. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Willey & Sons: New York, NY, USA, 1980. [Google Scholar]
- Fletcher, A.L.; Sinclair, T.R.; Allen, L.H., Jr. Transpiration responses to vapor pressure deficit in well watered ‘slow-wilting’and commercial soybean. Environ. Exp. Bot. 2007, 61, 145–151. [Google Scholar] [CrossRef]
- Fuchs, M.; Stanghellini, C. The functional dependence of canopy conductance on water vapor pressure deficit revisited. Int. J. Biometeorol. 2018, 62, 1211–1220. [Google Scholar] [CrossRef] [PubMed]
- Oren, R.; Sperry, J.; Katul, G.; Pataki, D.; Ewers, B.; Phillips, N.; Schäfer, K. Survey and synthesis of intra-and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant Cell Environ. 1999, 22, 1515–1526. [Google Scholar] [CrossRef] [Green Version]
- Rawson, H.; Begg, J.; Woodward, R. The effect of atmospheric humidity on photosynthesis, transpiration and water use efficiency of leaves of several plant species. Planta 1977, 134, 5–10. [Google Scholar] [CrossRef]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef] [Green Version]
- Stewart, J. Modelling surface conductance of pine forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Stewart, J. On the use of the Penrnan-Monteith equation for determining area évapotranspiration. Estimation Areal Evapotranspiration 1987, 3–12. [Google Scholar]
- Jarvis, P. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Ritchie, J.T.; Nesmith, D.S. Temperature and crop development. In Modeling Plant and Soil Systems; Amer Society of Agronomy: Madison, WI, USA, 1991; pp. 5–29. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993; Volume 9780070. [Google Scholar]
- Mishra, V.; Cruise, J.F.; Mecikalski, J.R.; Hain, C.R.; Anderson, M.C. A remote-sensing driven tool for estimating crop stress and yields. Remote Sens. 2013, 5, 3331–3356. [Google Scholar] [CrossRef] [Green Version]
- Tadesse, T.; Senay, G.B.; Berhan, G.; Regassa, T.; Beyene, S. Evaluating a satellite-based seasonal evapotranspiration product and identifying its relationship with other satellite-derived products and crop yield: A case study for Ethiopia. Int. J. Appl. Earth Obs. Geoinf. 2015, 40, 39–54. [Google Scholar] [CrossRef] [Green Version]
- Teixeira, D.C.; Antônio, H.; Scherer-Warren, M.; Hernandez, F.B.; Andrade, R.G.; Leivas, J.F. Large-scale water productivity assessments with MODIS images in a changing semi-arid environment: A Brazilian case study. Remote Sens. 2013, 5, 5783–5804. [Google Scholar] [CrossRef] [Green Version]
- Boulet, G.; Delogu, E.; Saadi, S.; Chebbi, W.; Olioso, A.; Mougenot, B.; Fanise, P.; Lili-Chabaane, Z.; Lagouarde, J.-P. Evapotranspiration and evaporation/transpiration partitioning with dual source energy balance models in agricultural lands. Proc. Int. Assoc. Hydrol. Sci. 2018, 380, 17–22. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Kustas, W.P.; Hain, C.R.; Cammalleri, C.; Gao, F.; Yilmaz, M.; Mladenova, I.; Otkin, J.; Schull, M.; Houborg, R. Mapping surface fluxes and moisture conditions from field to global scales using ALEXI/DisALEXI. In Remote Sensing of Energy Fluxes and Soil Moisture Content; CRC Press: Boca Raton, FL, USA, 2013; pp. 207–232. [Google Scholar]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Mladenova, I.E.; Basara, J.B.; Svoboda, M. Examining rapid onset drought development using the thermal infrared–based evaporative stress index. J. Hydrometeorol. 2013, 14, 1057–1074. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M. Examining the relationship between drought development and rapid changes in the evaporative stress index. J. Hydrometeorol. 2014, 15, 938–956. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef] [Green Version]
- Jaafar, H.H.; Ahmad, F.A. Time series trends of Landsat-based ET using automated calibration in METRIC and SEBAL: The Bekaa Valley, Lebanon. Remote Sens. Environ. 2020, 238, 111034. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- De Bruin, H.; Stricker, J. Evaporation of grass under non-restricted soil moisture conditions. Hydrol. Sci. J. 2000, 45, 391–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. Regionalization of Surface Flux Densities and Moisture Indicators in Composite Terrain: A Remote Sensing Approach under Clear Skies in Mediterranean Climates; DLO Winand Staring Centre: Wageningen, The Netherlands, 1995. [Google Scholar]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Chen, J.; Rao, Y.; Yamaguchi, Y. A combination of TsHARP and thin plate spline interpolation for spatial sharpening of thermal imagery. Remote Sens. 2014, 6, 2845–2863. [Google Scholar] [CrossRef] [Green Version]
- Lhomme, J.-P.; Elguero, E. Examination of evaporative fraction diurnal behaviour using a soil-vegetation model coupled with a mixed-layer model. Hydrol. Earth Syst. Sci. 1999, 3, 259–270. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; MacMillan, R.A. Predictive Soil Mapping with R; Lulu Press: Morrisville, NC, USA, 2019. [Google Scholar]
- Scott, C.; Bastiaanssen, W.; Ahmad, M. Mapping spatio-temporal distributions of soil moisture throughout irrigated watersheds using optical and high resolution imagery. J. Irrig. Drain. Eng. ASCE 2003, 129, 326–335. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.G.; Pelgrum, H.; Droogers, P.; De Bruin, H.A.; Menenti, M. Area-average estimates of evaporation, wetness indicators and top soil moisture during two golden days in EFEDA. Agric. For. Meteorol. 1997, 87, 119–137. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O.; Businger, J.A.; Fritschen, L.J.; Jensen, M.E.; Quinn, F.H. Evaporation and Transpiration. In Hydrology Handbook; American Society of Civil Engineers: New York, NY, USA, 1996; pp. 125–252. [Google Scholar]
- Ritchie, J.T.; Burnett, E. Dryland evaporative flux in a subhumid climate: II. Plant influences 1. Agron. J. 1971, 63, 56–62. [Google Scholar] [CrossRef]
- Sutanto, S.J.; Wenninger, J.; Coenders-Gerrits, A.M.J.; Uhlenbrook, S. Partitioning of evaporation into transpiration, soil evaporation and interception: A comparison between isotope measurements and a HYDRUS-1D model. Hydrol. Earth Syst. Sci. 2012, 16, 2605–2616. [Google Scholar] [CrossRef] [Green Version]
- Gillies, R.R.; Carlson, T.N. Thermal remote sensing of surface soil water content with partial vegetation cover for incorporation into climate models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef] [Green Version]
- Purevdorj, T.S.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between percent vegetation cover and vegetation indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- Hoogmoet, G.; Klop, S.; Mulder, E.; Nederlof, I.; Vleugels, J.; van der Vliet, N. Water Productivity Assessment of Rice Paddies in Indonesia; Master Project Report; Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- Allen, R.G.; Wright, J.L. Translating wind measurements from weather stations to agricultural crops. J. Hydrol. Eng. 1997, 2, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Venancio, L.P.; Mantovani, E.C.; do Amaral, C.H.; Neale, C.M.U.; Gonçalves, I.Z.; Filgueiras, R.; Campos, I. Forecasting corn yield at the farm level in Brazil based on the FAO-66 approach and soil-adjusted vegetation index (SAVI). Agric. Water Manag. 2019, 225, 105779. [Google Scholar] [CrossRef]
- Campoy, J.; Campos, I.; Plaza, C.; Calera, M.; Bodas, V.; Calera, A. Estimation of harvest index in wheat crops using a remote sensing-based approach. Field Crops Res. 2020, 256, 107910. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorologische Zeitschrift 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Rubel, F.; Brugger, K.; Haslinger, K.; Auer, I. The climate of the European Alps: Shift of very high resolution Köppen-Geiger climate zones 1800–2100. Meteorologische Zeitschrift 2017, 26, 115–125. [Google Scholar] [CrossRef]
- Fermont, A.; Benson, T. Estimating Yield of Food Crops Grown by Smallholder Farmers; International Food Policy Research Institute: Washington, DC, USA, 2011; Volume 1, p. 68. [Google Scholar]
- French, R.; Schultz, J. Water use efficiency of wheat in a Mediterranean-type environment. I. The relation between yield, water use and climate. Aust. J. Agric. Res. 1984, 35, 743–764. [Google Scholar] [CrossRef]
- Hicke, J.A.; Lobell, D.B. Spatiotemporal patterns of cropland area and net primary production in the central United States estimated from USDA agricultural information. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Villalobos, F.J.; Fereres, E. Principles of Agronomy for Sustainable Agriculture; Springer: Berlin, Germany, 2016. [Google Scholar]
- Lobell, D.; Hicke, J.; Asner, G.; Field, C.; Tucker, C.; Los, S. Satellite estimates of productivity and light use efficiency in United States agriculture, 1982–1998. Glob. Chang. Biol. 2002, 8, 722–735. [Google Scholar] [CrossRef]
- Nonhebel, S. Estimating yields of biomass crops in the Netherlands. Zemedelská Technika 1995, 41, 59–64. [Google Scholar]
- Van Elderen, E.; Van Hoven, S. Moisture content of wheat in the harvesting period. J. Agric. Eng. Res. 1973, 18, 71–93. [Google Scholar] [CrossRef]
- Bocianowski, J.; Nowosad, K.; Szulc, P. Soil tillage methods by years interaction for harvest index of maize (Zea mays L.) using additive main effects and multiplicative interaction model. Acta Agric. Scand. Sect. B Soil Plant Sci. 2019, 69, 75–81. [Google Scholar] [CrossRef]
- O’Shaughnessy, S.A.; Andrade, M.A.; Evett, S.R. Using an integrated crop water stress index for irrigation scheduling of two corn hybrids in a semi-arid region. Irrig. Sci. 2017, 35, 451–467. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.G.; Guan, Z.-H.; Jia, B.; Turner, N.C.; Li, F.-M. The effects of plastic-film mulch on the grain yield and root biomass of maize vary with cultivar in a cold semiarid environment. Field Crops Res. 2018, 216, 89–99. [Google Scholar] [CrossRef]
- Gaile, Z. Harvest time effect on yield and quality of maize (Zea mays L.) grown for silage. Latv. J. Agron. Agronomija Vestis 2008, 105–111. [Google Scholar]
- dos Santos, H.; Carvalho Junior, W.d.; Dart, R.d.O.; Áglio, M.; de Sousa, J.; Pares, J.; Fontana, A.; Martins, A.d.S.; de Oliveira, A. O novo mapa de solos do Brasil: Legenda atualizada; Embrapa Solos-Documentos (INFOTECA-E); Embrapa Solos: Rio de Janeiro, Brazil, 2011. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Qian, B.; Jing, Q.; Croft, H.; Chen, J.; Wang, J.; Huffman, T.; Shang, J.; Chen, P. Deriving maximum light use efficiency from crop growth model and satellite data to improve crop biomass estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 104–117. [Google Scholar] [CrossRef]
- Saha, S.; Nadiga, S.; Thiaw, C.; Wang, J.; Wang, W.; Zhang, Q.; Van den Dool, H.; Pan, H.-L.; Moorthi, S.; Behringer, D. The NCEP climate forecast system. J. Clim. 2006, 19, 3483–3517. [Google Scholar] [CrossRef] [Green Version]
- Van Hoolst, R.; Eerens, H.; Haesen, D.; Royer, A.; Bydekerke, L.; Rojas, O.; Li, Y.; Racionzer, P. FAO’s AVHRR-based Agricultural Stress Index System (ASIS) for global drought monitoring. Int. J. Remote Sens. 2016, 37, 418–439. [Google Scholar] [CrossRef]
- Campos, I.; González-Gómez, L.; Villodre, J.; Calera, M.; Campoy, J.; Jiménez, N.; Plaza, C.; Sánchez-Prieto, S.; Calera, A. Mapping within-field variability in wheat yield and biomass using remote sensing vegetation indices. Precis. Agric. 2019, 20, 214–236. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui Valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ. 2003, 94, 205–220. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; van der Werf, G.R.; Dolman, A.J.; Groenendijk, M. Evaluation of cropland maximum light use efficiency using eddy flux measurements in North America and Europe. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Pan, Y.; He, H.; Yu, D.; Hu, H. Simulation of maximum light use efficiency for some typical vegetation types in China. Chin. Sci. Bull. 2006, 51, 457–463. [Google Scholar] [CrossRef]
- McMaster, G.S.; Ascough II, J.C.; Edmunds, D.A.; Nielsen, D.C.; Prasad, P.V. Simulating crop phenological responses to water stress using the PhenologyMMS software program. Appl. Eng. Agric. 2013, 29, 233–249. [Google Scholar] [CrossRef]
- González-Gómez, L.; Campos, I.; Calera, A. Use of different temporal scales to monitor phenology and its relationship with temporal evolution of normalized difference vegetation index in wheat. J. Appl. Remote Sens. 2018, 12, 026010. [Google Scholar] [CrossRef]
- Mourad, R.; Jaafar, H.; Anderson, M.; Gao, F. Assessment of Leaf Area Index Models Using Harmonized Landsat and Sentinel-2 Surface Reflectance Data over a Semi-Arid Irrigated Landscape. Remote Sens. 2020, 12, 3121. [Google Scholar] [CrossRef]
- Ochieng, H.O.; Ojiem, J.; Otieno, J. Farmer versus Researcher data collection methodologies: Understanding variations and associated trade-offs. AfricArXiv 2019. [Google Scholar] [CrossRef] [Green Version]
- Arslan, S.; Colvin, T.S. Grain yield mapping: Yield sensing, yield reconstruction, and errors. Precis. Agric. 2002, 3, 135–154. [Google Scholar] [CrossRef]










| Study Site | Crop | Actual Yield (t/ha) | Number of Observations | Average Field Size | Data Reference | |
|---|---|---|---|---|---|---|
| Min. | Max. | (ha) | ||||
| Skaff, Bekaa (Lebanon) | Potato | 34 | 52 | 31 | 23 | Recall method |
| Wheat | 5 | 8 | 21 | 24 | ||
| Desidério (Brazil) | Corn | 10.5 | 13.5 | 27 | 89 | [95] |
| Albacete (Spain) | Wheat | 1.2 | 8.7 | 9 | 24 | [96] |
| Agricultural Research and Education Center (AREC), Bekaa (Lebanon) | Potato | Value: 68.75 | 1 | 0.95 | Measured | |
| Crop | Used HI (%) | HI (%) Literature | HI References | Crop Moisture Content Used in This Study (%) | Crop Moisture Content (%) Literature | References |
|---|---|---|---|---|---|---|
| Wheat | 0.4 | 0.29–0.48 | [100,101,102] | 0.15 | 0.1–0.18 | [103,104,105] |
| Potato | 0.75 | 0.5–0.75 | [101,102] | 0.75 | 0.70–0.85 | [103,104] |
| Corn | 0.45 | 0.35–0.6 | [106,107,108] | 0.28 | Min. 0.25 Optimum 0.28–0.30 | [103,109] |
| Model Inputs | Spatial Resolution | Temporal Resolution | Possible Uncertainties |
|---|---|---|---|
| CFSv2 (used to derive weather variables) | ∼0.2° | 6 hr | In complex topography–plain interfaces, pixels might not be reflective of local conditions; could be overcome by downscaling weather data using Machine Learning (ML) techniques/adiabatic lapse rate. |
| Landsat 7 ETM+ and Landsat 8 OLI/TIRS imagery data | 30 m | Weekly | Uncertainty due to the presence of clouds, leading to limited observations/uncertainty due to scanline corrector gap filling. |
| Soils’ Open Land Map Earth Engine dataset | 250 m | Resolution might not be enough when soils are heterogeneous at a larger scale; percentage clay, sand, and silt might differ from field conditions, leading to different estimates of soil moisture when the available soil water capacity is different than what is calculated. | |
| Harvest index (HI) | _ | _ | Venancio [95] showed that the use of specific HI values could decrease the difference between the predicted and the measured yield from ±10% (with the use of a single HI value) to ±5% (with the use of a specific HI value); the used HI in this study falls within the reported range, indicating less uncertainty in crop yield estimation. |
| LUEmax | _ | _ | Dong et al. [112] showed significant improvements in biomass estimation accuracy when using the derived variable LUEmax (by about 15.0% for the normalized root-mean-square error (nRMSE)) compared to the fixed LUEmax. |
| Agrometeorological Data | Description | Unit |
|---|---|---|
| Temp | Temperature 2 m above ground | °K |
| U-wind | U-component of wind 10 m above ground | m/s |
| V-wind | V-component of wind 10 m above ground | m/s |
| Relative Humidity (RH) spec | Specific humidity 2 m above ground | Kg/kg |
| Pressure surface | Pressure at surface | Pa |
| Skaff, Bekaa (Lebanon) | São Desidério (Brazil) | Albacete (Spain) | |||||
|---|---|---|---|---|---|---|---|
| Crop | Potato (n = 31) | Wheat (n = 21) | Corn (n = 27) | Wheat (n = 9) | |||
| Season | Summer 2017 (n = 16) | Summer 2018 (n = 15) | Winter 2017–2018 (n = 21) | 2015 (n = 13) | 2016 (n = 14) | 2017 (n = 6) | 2018 (n = 3) |
| Average reported yield (t/ha) | 40 | 43 | 6.9 | 12.10 | 12.47 | 4.1 | 2.3 |
| Average modeled yield (t/ha) | 38 | 42 | 6.8 | 12.25 | 13.12 | 4.3 | 2.6 |
| Root-mean-square error (RMSE) (t/ha) | 3.74 | 4.25 | 0.64 | 1.06 | 1.5 | 0.29 | 0.26 |
| Mean absolute error (MAE) (t/ha) | 3.1 | 3.8 | 0.5 | 0.8 | 1.2 | 0.22 | 0.25 |
| Mean bias error (MBE) (t/ha) | −1 | −0.6 | −0.05 | 0.15 | 0.66 | 0.20 | 0.30 |
| Index of agreement, d | 0.6 | 0.6 | 0.8 | 0.5 | 0.4 | 0.99 | 0.8 |
| Relative error (RE) | 2.50% | 0.83% | 1.4% | −1.22% | −5% | −5% | −11% |
| Variable | Field ID 30P | Field ID 31P | % Difference (25–24) |
|---|---|---|---|
| Average moisture stress (SMS) | 0.665 | 0.754 | 12% |
| Average vapor stress (VS) | 0.841 | 0.841 | 0% |
| Average temperature stress (TS) | 0.886 | 0.886 | 0% |
| Average combined stress | 0.5 | 0.56 | 11% |
| Average modeled yield (t/ha) | 39 | 40 | 3% |
| Average reported yield (t/ha) | 35 | 42 | 17% |
| Parameter | Season | Average | Min. | Max. | Standard Deviation |
|---|---|---|---|---|---|
| LUE | 2017 | 0.8 | 0 | 2.1 | 0.7 |
| (g/MJ) | 2018 | 1 | 0.1 | 2.2 | 0.5 |
| 2017–2018 | 1.2 | 0 | 3 | 0.6 | |
| Reported yield | 2017 | 39.5 | 34 | 46 | 3.7 |
| (t/ha) | 2018 | 42.7 | 35 | 52 | 4.3 |
| 2017–2018 | 6.86 | 5 | 8 | 0.7 | |
| Modeled yield | 2017 | 38.5 | 35 | 42 | 2.7 |
| (t/ha) | 2018 | 42 | 37 | 49 | 3.7 |
| 2017–2018 | 6.81 | 5 | 8 | 0.8 | |
| Moisture stress | 2017 | 0.4 | 0 | 1 | 0.4 |
| 2018 | 0.5 | 0 | 1 | 0.3 | |
| 2017–2018 | 0.5 | 0 | 1 | 0.3 | |
| Vapor stress | 2017 | 0.9 | 0.7 | 1 | 0.1 |
| 2018 | 0.8 | 0.7 | 1 | 0.1 | |
| 2017–2018 | 0.9 | 0.7 | 1 | 0.1 | |
| Temperature stress | 2017 | 0.8 | 0.3 | 1 | 0.2 |
| 2018 | 0.9 | 0.5 | 1 | 0.1 | |
| 201–2018 | 0.9 | 0.5 | 1 | 0.1 | |
| Combined stresses | 2017 | 0.288 | 0 | 1 | 0.008 |
| 2018 | 0.36 | 0 | 1 | 0.003 | |
| 2017–2018 | 0.405 | 0 | 1 | 0.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaafar, H.; Mourad, R. GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data. Remote Sens. 2021, 13, 773. https://doi.org/10.3390/rs13040773
Jaafar H, Mourad R. GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data. Remote Sensing. 2021; 13(4):773. https://doi.org/10.3390/rs13040773
Chicago/Turabian StyleJaafar, Hadi, and Roya Mourad. 2021. "GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data" Remote Sensing 13, no. 4: 773. https://doi.org/10.3390/rs13040773
APA StyleJaafar, H., & Mourad, R. (2021). GYMEE: A Global Field-Scale Crop Yield and ET Mapper in Google Earth Engine Based on Landsat, Weather, and Soil Data. Remote Sensing, 13(4), 773. https://doi.org/10.3390/rs13040773