1. Introduction
The spatial position consistency of the same objects in multiple images guarantees the subsequent applications accuracy of remote sensing [
1,
2], medical imaging [
3,
4] and computer vision fields [
5,
6]. It is usually enforced by the means of geometric registration, which is a process of aligning different images of the same scene acquired at different times, viewing angles, and/or sensors [
7].
In particular, quite a few algorithms have been proposed over the past decades for remote sensing images registration, broadly falling into two categories [
8,
9], i.e., the area-based methods and the feature-based methods. The area-based methods register images with their intensity information directly, whereas they are disabled to cope with large rotation and scale changes [
10]. Consequently, more attention has been paid to feature-based methods [
10,
11,
12,
13,
14,
15,
16]. The sensed image is aligned to the reference image by their significant geometrical features rather than intensity information, including feature extraction, feature matching, transformation model construction, coordinate transformation, and resampling [
14]. Taking the feature point extraction as an example, the scale-invariant feature transform (SIFT) [
17], the speeded-up robust feature (SURF) [
18], and the extended SIFT or SURF [
15,
16] are well-known operators. The exhaustive search method [
17] and the KD-tree matching algorithm are popular representatives of feature matching. The random sample consensus (RANSAC) [
19] or maximum likelihood estimation sample consensus (MLESAC) [
20] is applied to purify the matched features [
21], namely outliers elimination. Successively, designing the geometric relationships for coordinate transformation, the global transformation model is the traditional and typical representation [
9], which usually results in local misalignments for local and complicated deformations.
The local transformation model designs varied mapping functions for a whole image, including piecewise linear mapping function (PLM) [
22], weighted mean (WM), multiquadric (MQ) [
23], thin-plate spline (TPS) [
24], and two-stage local registration model BWP-OIS [
25]. The registration accuracy of the local model highly depends on the modeling type and is further determined by the distribution, number and position precision of feature points [
23]. Nevertheless, the feature point extraction of the complex-terrain image is arduous due to the monotonous texture and degraded image quality. In addition, the pixel correspondences between images destroyed by varied geometric deformations could not be precisely acquired by current local models [
26]. That is to say, it is difficult to achieve high-precision registration in the complex-terrain region under the feature-based framework although it performs well in most scenarios. To this end, a pixel-wise registration method should be taken into consideration.
Optical flow estimation is a pixel-wise algorithm firstly introduced by Horn and Schunch [
27] in the field of computer vision for motion estimation. Afterwards, some modified models are proposed for high-precision motion estimation of video images [
28,
29]. As the geometric deformation of the corresponding pixels in multiple remote sensing images is similar to the object motions in successive frames, the optical flow algorithm was available for remote sensing images registration. However, its applications are rare in the remote sensing field. Only in recent years, the sparse optical flow algorithm is conducted for multi-modal remote sensing images registration on a single scenario, which does not need to process the abnormal displacements caused by land use or land cover (LULC) changes [
26,
30,
31].
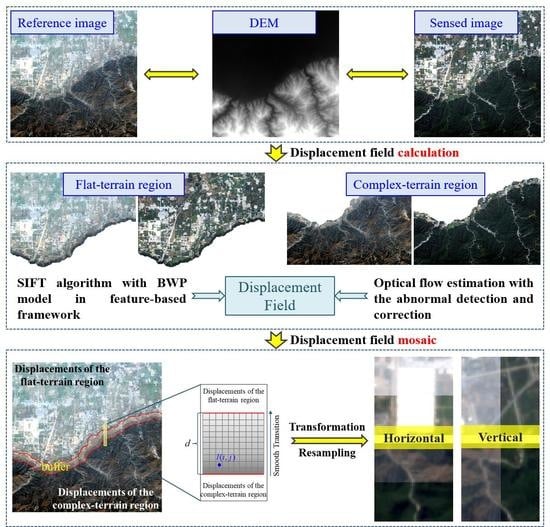
Due to the large field of view, a remote sensing image generally covers a large scene, containing the residential region, mountainous region, and agricultural region, etc. simultaneously. Different regions in the same scene involve locally varied geometric distortions with the topographic relief, for example, the complicated deformation in the complex-terrain region and locally consistent geometric distortion in the flat-terrain region. Moreover, LULC changes are frequent phenomena in multiple remote sensing images, which is an obstacle for pixel-wise registration algorithms to some extent. For the aforementioned two points, we propose a region-by-region registration combining feature-based and optical flow algorithms for remote sensing image, which is based on the mosaic of their individual displacement field. The main contributions of this paper include two aspects. One gives a novel region-by-region registration framework achieving highly precise registration of the whole scene considering the topographic relief. The other is to propose a correction approach for abnormal optical flow field caused by the LULC changes, integrating the adaptive detection and seamless correction by the weighted Taylor expansion.
The rest of this paper is organized as follows. The details of the proposed registration method are introduced in
Section 2. The experimental results and verification from the visual and quantitative perspectives are provided in
Section 3. Subsequently, the core parameter analysis is performed in
Section 4. Finally, our conclusions are summarized in
Section 5.
3. Experiments and Evaluations
In this section, four representative pairs of remote sensing images in
Table 1 were testified to evaluate the proposed algorithm qualitatively and quantitatively. Firstly, the results of the proposed method were visually compared with those of three local transformation models under the feature-based framework and the original optical flow estimation, i.e., PLM [
22], TPS [
24], BWP-OIS [
25], and BOF [
36]. PLM designs a series of local affine transformation models for each triangle constructed by the extracted feature points [
22]. TPS estimates the geometrical relationship between the reference and sensed image by a systematic affine transformation model and a weighted radial basis function for considering local distortion [
24]. BWP-OIS locally registers images in a two-step process by integrating the block-weighted projective transformation model and the outlier-insensitive model [
25]. BOF registers the image by directly transforming the coordinates and resampling with pixel-wise displacements calculated under the brightness consistency and the gradient consistency [
36]. Secondly, three assessment indicators were used for quantitative evaluation in
Section 3.2, including root-mean-square error (RMSE), normal mutual information (NMI), and correlation coefficients (CC).
3.1. Visual Judgment
The registration results of the proposed algorithm are shown in
Figure 6. As seen from the original images in
Figure 6a,b, they show a large radiation difference (“test-I”), or are contaminated by uneven clouds (“test-II”), or include typical hybrid terrain region (“test-III”), or cover the complicated terrain (“test-IV”). The terrain mask is calculated by TR in Equation (1) and shown in
Figure 6c. The white pixels represent the complex-terrain region and the black ones mean the flat-terrain region. They are approximately consistent with the visual observation and elevation data. Especially, since the test-IV images are located in Chongqing, China, which is known as the "mountain city", most of the image is in the complex-terrain region and they are white in the terrain mask. The overlapping results of the original images in
Figure 6d show blurs and ghosts, which indicates that the geometrical deformation exists between reference and sensed images. By contrast, the overlapping results of aligned images by the proposed algorithm in
Figure 6e are visually clear and distinctive. In other words, the experiments demonstrate the effectiveness of the proposed algorithm.
Successively, the comparison results of the proposed algorithm and other comparative methods are shown in
Figure 7, which are the enlarged sub-regions of the red and green dotted-rectangle regions in
Figure 6a for fine comparisons. The vertical alignment is labeled with red “
A” and the horizontal alignment is marked with green “
B”. The boundaries of the reference and aligned images are available to judge the registration accuracy. The white arrows and filled circles are auxiliary to indicate the displacements between the reference and aligned image. The arrows depict the direction of misalignment and their lengths are proportional to the amount of dislocation from the aligned image to the reference image. The white filled circles represent the well-registered results.
While focusing on the first comparison for “test-I” in
Figure 7, row “
A” shows the vertical registration of different methods. The “Original” broken linear features mean a large vertical deformation between the reference and sensed images. PLM and TPS eliminate the most of vertical deformation, but not completely. BWP-OIS results in overcompensation [
25] to the sensed image so that the opposite misalignment of the linear features is introduced on the boundary. BOF and the proposed algorithm achieve highly accurate registration, where the linear features are continuous and smooth at the same position. For row “
B”, though most of the horizontal displacements have been eliminated, the results of PLM and TPS still have dislocations. BWP-OIS, BOF, and the proposed algorithm register the sensed image well. However, the abnormal objects are introduced by BOF, which are not visible in the aligned image of the proposed method, marked with the white dotted ellipses. Therefore, the proposed algorithm gives high registration accuracy and guarantees the content against changes simultaneously.
The second comparison is for “test-II” in
Figure 7. In Row “
A”, the road at the bottom and the edge of the second Chinese character on the top are used to judge the registration result. The second Chinese character should be symmetrical, whereas its left and right parts are asymmetries due to the vertical dislocation. Although PLM aligns the road continuously and smoothly, the deformation of the second Chinese character is magnified. TPS could not align the sensed image well to the reference image. The Chinese character is aligned by BWP-OIS, but the road is not continuous. Fortunately, BOF and the proposed algorithm obtain the well-aligned outcomes for the road and the second Chinese character. However, the road on the result of BOF is changed. In “
B” row, the road in the sensed image is shifted a lot to right by PLM and TPS. The proposed algorithm, BOF, and BWP-OIS provide the desired alignments. The only drawback is the content of the sensed image is altered by BOF. Therefore, PLM and TPS fail to align the sensed image to the reference image spatially. BWP-OIS gives desirable registration in the horizontal direction but not in the vertical direction. BOF generates accurate alignments accompanied by abnormal changes marked with white dotted ellipses. The proposed algorithm outperforms others in alignment with accuracy or content fidelity.
The selected regions in “test-III” and “test-IV” in
Figure 6 further verify the proposed algorithm, as shown in
Figure 7. For “test-III” in
Figure 7, a similar phenomenon is observed, where the proposed algorithm outperforms others both in the vertical and horizontal directions. The phenomenon of the content change introduced by BOF is removed by the proposed algorithm. For “test-IV” in
Figure 7, the other three algorithms excluding PLM provide the well-aligned outcomes in “
A” row. In “
B” row (test-IV), PLM and TPS widen the dislocation, and BWP-OIS introduces the opposite misalignment of the bridge. BOF and the proposed algorithm completely eliminate the deformation and the bridge is connected smoothly and continuously. However, BOF changes the content (labeled by a white dotted ellipse), and the proposed algorithm keeps the content of the sensed image well. In conclusion, the proposed algorithm visually outperforms other algorithms in all experiments. To further evaluate the proposed algorithm, the quantitative evaluation is conducted.
3.2. Quantitative Evaluation
The quantitative evaluation with three indictors was further used for verifying the visual judgment. On one hand, RMSE depicts the spatial registration accuracy. On the other hand, NMI and CC judge the similarity between the aligned image and the reference image according to their corresponding pixel values.
The RMSE focuses on evaluating the registration result by calculating the average distance of the corresponding points in the reference and aligned image. As most literature did, some distinct feature points from the corresponding reference and aligned images were extracted manually to calculate their RMSE [
7,
40]. RMSE of the comparative algorithms is listed in
Table 2. The feature points for evaluation are extracted manually and the number is listed in brackets. “Original” means the RMSE of the reference and sensed image before registration. All the algorithms relieve the geometric distortion of the reference and sensed image as shown in
Table 2. TPS gives the largest RMSE among all registration algorithms. BWP-OIS performs better than PLM in the last three experiments. The smallest RMSE is obtained by the proposed algorithm and the suboptimal performance is given by BOF. Since there are some abnormal objects and pseudo traces in the aligned image of BOF, these anomalies change the shape or the original track of linear features in the aligned image, causing lower registration accuracy. The proposed algorithm performs better than the three feature-based algorithms, which means that it is more favorable for registering complex-terrain regions. Furthermore, RMSE of the proposed algorithm is smaller than that of BOF, indicating that the feature-based method owns the similar registration accuracy without being affected by the LULC changes in the flat-terrain region, and the proposed algorithm copes with the LULC changes in the complex-terrain region well.
To further evaluate the performance of the proposed method, we extract the complex-terrain region of the aligned image and the corresponding part in the reference image. The extracted ones of the above experiments are conducted to calculate the NMI and CC shown in
Figure 8a,b. NMI and CC are the similarity criteria, usually employing as the iteration termination condition in the area-based registration algorithm. The NMI index measures the statistical correlation of images, which is defined as follows:
where
and
are the entropy of images
and
, respectively.
is the joint entropy of two images. Larger NMI correspond to a greater similarity between two images. The CC value of images
and
is calculated as:
where
denotes covariance between two images.
and
are the standard deviations of two images, respectively. Since CC could range from −1 to 1, 1 indicates perfect correlation.
As shown, the proposed method achieves the largest NMI and CC in all the experiments. The registration accuracy of PLM is close to that of BWP-OIS whereas the latter is slightly superior in “test-III” and “test-IV” in
Figure 8. The local mapping functions of PLM are constructed by feature points, so its accuracy is limited by the precision of the feature points extraction. On that account, BWP-OIS alleviates the situation by designing the transformation functions with all feature points in different weights. Therefore, BWP-OIS performs better than PLM in most instances. Additionally, TPS gets the worst registration accuracy in four experiments, which is suitable for images with dense and uniformly distributed feature points [
23]. It is difficult to extract feature points in the complex-terrain region, especially points with uniform distribution. In addition, the registration accuracy of BOF is comparable to the proposed method in the complex-terrain regions when evaluating with NMI and CC, which is similar to the RMSE result. In addition, it is worth noting that there is a big jump on test-I. It is because there is a large deformation between the reference and sensed images, resulting in the smaller NMI and CC compared with those of the registration results. On the one hand, not only the local region rounded with yellow rectangles of test-I in
Figure 5 presents an obvious geometric dislocation; but the RMSE of the test-I original images in
Table 2 is larger than those of other experiments. Hence, there is a big jump in
Figure 8 of NMI and CC values on test-I. The proposed method automatically registers images, including image division according to the terrain characteristics, alignment of flat-terrain region with feature-based algorithm, the pixel-wise displacement calculation of complex-terrain region with improved optical flow estimation. The thresholds in these steps are determined with the experience of a large number of experiments. The evaluation demonstrates that the proposed method performs well on the mixed-terrain region compared with the conventional feature-based methods and the original optical flow algorithm. To a certain extent, it also shows that the scheme of region-by-region registration is feasible.
4. Discussions
The previous section validated the registration result of the proposed method. This section focuses on core parameter analysis. The main parameter is the LED threshold for the terrain division, determining the algorithm utilized to register the local region of images and further influencing the final registration accuracy.
for terrain division determines that a pixel should be divided into the complex terrain region or flat-terrain region, which further influences the overall registration accuracy. To reveal the relationship, a series of experiments were conducted with different thresholds. Without loss of generality, the aforementioned experimental data in
Figure 6 is employed, with the threshold varied from five to thirteen. The quantitative evaluation results of the final registration with varied thresholds are shown in
Table 3, with the evaluation indicators of NMI and CC.
For the four groups of experiments, with the increase in the threshold, the two indicators are at first small fluctuations, or even stable, and then decrease, showing the relatively simple relationship. However, focusing on the quantitative evaluation of “test-III”, the largest NMI is obtained when the LED threshold is set as eight whereas the best CC is generated while equals six. Except for the third experiment, they share the same phenomenon, in that the optimal registration results are obtained while the LED threshold is set as seven. When the threshold is larger than seven, more pixels are put into the flat-terrain region whereas the complex terrain is in practice, weakening the registration accuracy. However, this does not mean that the smaller the threshold is, the higher the registration accuracy will be, such as the third and fourth groups of the experiments. However, when the available range of LED threshold is five to eight, the indicators do not show an obvious difference, where the largest numerical difference is 0.0008. Under this circumstance, the difference between the different registration results could not be caught by the eyes. After the comprehensive consideration, the LED threshold was determined to be seven in the experiments.
For conveniently applying this technique, taking test-III as an example, the terrain masks generated by different thresholds are listed in
Figure 9. The intention is to divide the image to be registered into multiple local regions with flat- and complex-terrain characteristics. That is to say, the heterogeneous features distributed in a topographic block are not put into this block as far as possible. Therefore, the hole-filling algorithm and the morphological expansion approach are utilized, as described in
Section 2.1. Before the post-processing of the terrain mask, the generated mask should provide an ideal foundation. The threshold of LED for terrain division is set with the visual observation and the quantitative evaluation of registration result. In
Figure 9, the black indicates the complex-terrain region, and white means the flat-terrain region. When the threshold is 5, there are heterogeneous and small blobs both in the complex- and flat-terrain regions. While the threshold is 7, there are relatively few heterogeneous blobs in the flat-terrain region (denoted in white), and more white blobs in the complex-terrain region, compared with the first two masks. When compared with the last six masks, the terrain division is relatively regular, namely most flat-terrain pixels are in the white region and complex-terrain blobs are in black. The conclusion is similar to
Table 3. Not only test-III but three other experiments also give a similar conclusion, which is not shown here. Therefore, after quantitative comparison and qualitative observation of a large number of experiments, we provide the available range of the threshold
in
Section 2.1 and the best recommended threshold is seven.
5. Conclusions
In this paper, we proposed a region-by-region registration combining feature-based and optical flow methods for remote sensing images. The proposed method innovatively makes use of the geometric deformation characteristic varied with regions caused by the topographic relief, registering flat- and complex-terrain regions, respectively. Owing to the pixel-wise displacement estimation of dense optical flow algorithm, the registration accuracy in complex-terrain region is reinforced. Moreover, the adaptive detection and weighted Taylor expansion enforced makes up for the defect of the abnormal displacements in the LULC changed region, which is sensitive for dense optical flow estimation. In other words, the feature-based method, dense optical flow estimation, adaptive detection technique, and weighted Taylor expansion are all employed for high-precision pixel-wise displacements, further for accurate registration. The accuracy of the complex-terrain region determines the whole registration precision of images covering the mixed terrain, which has attracted much attention in the proposed framework, and is realized by improving the optical flow algorithm. As confirmed in the experiments, the proposed approach outperforms the conventional feature-based methods and the original optical flow algorithm, not only qualitatively, but also quantitatively, from the aspects of visual observation, NMI, CC and RMSE.
However, the proposed method is just an interesting first trial of mixed-terrain images registration. The result is preliminary, and there is still room for improvement. For instance, when the experiments are conducted on Matlab2018a settled on computer with an Intel (R) Xeon (R) CPU E5-2650 v2 2.6GHz, the runtime of our experiments is 295.237s, 294.044s, 373.050s, and 143.808s respectively. It is time-consuming to register images by the proposed algorithm, which exceeds the expected time of image registration in the pre-processing stage, even real-time processing. Therefore, the time efficiency needs to be improved with parallel processing on the C++ platform, particularly for the complex-terrain region alignment. Additionally, when registering two degraded images with optical flow algorithm in the complex-terrain region, both images are simultaneously contaminated at the same location and abnormal displacements could not be restored as the weight from phase congruency for Taylor expansion calculating abnormally, which further changes the aligned image content compared with sensed image. Moreover, more mixed-terrain images from other sensors should be further tested in experiments for our proposed method. These issues will be addressed in our future work.