Monitoring of the Production Process of Graded Concrete Component Using Terrestrial Laser Scanning

Abstract

Accepting the ecological necessity of a drastic reduction of resource consumption and greenhouse gas emissions in the building industry, the Institute for Lightweight Structures and Conceptual Design (ILEK) at the University of Stuttgart is developing graded concrete components with integrated concrete hollow spheres. These components weigh a fraction of usual conventional components while exhibiting the same performance. Throughout the production process of a component, the positions of the hollow spheres and the level of the fresh concrete have to be monitored with high accuracy and in close to real-time, so that the quality and structural performance of the component can be guaranteed. In this contribution, effective solutions of multiple sphere detection and concrete surface modeling based on the technology of terrestrial laser scanning (TLS) during the casting process are proposed and realized by the Institute of Engineering Geodesy (IIGS). A complete monitoring concept is presented to acquire the point cloud data fast and with high-quality. The data processing method for multiple sphere segmentation based on the efficient combination of region growing and random sample consensus (RANSAC) exhibits great performance on computational efficiency and robustness. The feasibility and reliability of the proposed methods are verified and evaluated by an experiment monitoring the production of an exemplary graded concrete component. Some suggestions to improve the monitoring performance and relevant future work are given as well.

1. Introduction

1.1. Background and Motivation

The building sector, especially the concrete industry, is one of the world’s largest consumers of natural resources and emitters of harmful greenhouse gases [1,2]. To increase resource efficiency and reduce the emissions, new technologies are needed that aim at minimizing component mass and embodied energy as well as enabling full recyclability [3]. One approach to reducing the weight of load-bearing concrete components is the use of graded concrete which was invented by Werner Sobek. This technology is based on a tailored design of the component interior [4]. Cavities of different shapes and sizes are arranged inside the component in such a way that a fully stressed design is achieved, which results in a full material utilization at every point in the component [4,5]. Compared to conventional concrete components, the weight of the graded component and the associated use of resources can be reduced by up to 50% with CO₂ savings of 30–40% while its performance is fully maintained [6,7,8]. The gradation inside the component can be achieved by different techniques. One approach is the so-called meso gradation, hereby hollow concrete bodies (e.g., hollow spheres in this contribution) are placed as close as possible to the interior of the component, as shown in Figure 1a. The positions and sizes of the hollow bodies depend on the stress situation in the component (Figure 1b).

The precise match of the intended and the actual position of each hollow sphere is of vital importance to the performance of the meso-graded component. A major challenge for the production is to ensure the precise position of the mineral hollow spheres and to maintain it throughout the production process. At the ILEK, a layer-by-layer casting process using self-compacting concrete was developed, which prevents the hollow spheres from floating when the concrete is cast [4,5]. This process begins after the hollow spheres and reinforcement are correctly placed and positioned in the formwork of the component. The positional stability of the spheres during production is influenced by two factors: the buoyancy forces inflicted on the hollow spheres by the liquid fresh concrete and the adhesion forces acting between the hardening concrete and the hollow spheres. Both the time between the casting of two layers and the height of each layer are chosen so that the adhesive forces together with the weight of the spheres always surmount the buoyancy forces.

Appropriate monitoring measures are required to meet the quality requirements of the production of weight-minimized graded concrete components. These must be able to precisely determine the positions and radii of the hollow spheres in the component with the accuracy at millimeter level. An undetected deviation between planning and execution can lead to a situation where the load-bearing capacity of a component no longer meets its requirements. The level of the fresh concrete surface is supposed to be monitored during the layer-by-layer casting process. A monitoring system needs to report on the positional stability of the hollow spheres throughout the production and needs to reconstruct the increasing concrete level in the formwork. All measurements and data processing should be completed in a short time before the concrete hardens. With the acquisition of these data, the casting process can be controlled in a targeted manner and the component can be produced in high quality in precise accordance with its design.

1.2. Choice of Sensors

According to the production requirements of the graded concrete component, high-precision and area-wise spatial data of the component surface is supposed to be acquired quickly and in a non-contact way. Close-range photogrammetry and terrestrial laser scanning (TLS) are efficient monitoring methods that meet the demands of this task. These two approaches are both able to capture abundant geometric information [10]. Compared with photogrammetry, however, TLS has higher accuracy and independence of texture and illumination of objects [11,12]. Without artificial targets attached to these concrete spheres, it will be difficult to detect these objects in images via the deficient and variable natural textures on them. Therefore, this study aims to develop a practical and reliable approach for monitoring the geometric parameters of the hollow spheres and concrete level within a short time by means of TLS. In this way, the data processing step can be regarded as hollow sphere detection and concrete surface modeling based on the 3D point cloud.

1.3. Algorithms for Sphere Detection

Spherical objects are crucial primitives found in 3D spatial data. Especially sphere targets are used extensively for camera and laser scanner calibration or data registration in which robust sphere detection and estimation are necessary to achieve good results [13,14,15]. Plenty of approaches for sphere segmentation or extraction from point cloud have been proposed, such as the clustering-based method [16,17], sampling-based method [14,18], and Hough transform-based method [19,20], etc. However, most of these methods more or less have limitations, including the robustness to outliers or noise, computation time, requirements for the exposed spherical area and prior information, etc. For instance, the clustering-based method using the normal vector and curvature enables multiple sphere detection without knowing the approximate position of the sphere [17]. For the detection of hollow spheres during the casting process, however, some fresh concrete may unintentionally drip on the spherical surface and result in wrong calculations of normal vectors and curvatures, probably leading to unsatisfactory clustering results. Besides, some advanced algorithms to handle the multiple sphere detection in a complicated environment may lead to more complexity and computational load [15], which cannot meet the time requirement in this monitoring task. Meanwhile, complex parameter tuning also makes these algorithms difficult to be applied to practical problems.

In order to avoid the high complexity and operational difficulty as well as guarantee the robustness in a changing scenario, the region growing (RG) and the random sample consensus (RANSAC) algorithms are considered for multiple sphere segmentation or detection from the 3D point cloud in this monitoring task due to their superiorities. RG was first proposed in the field of intensity image segmentation [21] and then was introduced to 3D point cloud segmentation [22,23,24,25,26]. This method has the advantage of unnecessary prior parameters of spheres (like the design of the sphere layout and the coordinate information). However, 3D RG may require a long time for the parameter tuning [27] and the calculation of normal vector and curvature. RANSAC was introduced as a general framework for model fitting in the presence of outliers [28]. Compared with RG-based segmentation, RANSAC enables the model (e.g., plane, cylinder and sphere) segmentation and estimation more robustly and rapidly under a complex circumstance containing lots of noise or outliers [29]. Nevertheless, only one model can be found in each segmentation. Supposing performing iterative segmentation to find expected models one by one, the proportion of inlier will decrease significantly, which may cause RANSAC to be unable to find models gradually within limited iterations.

1.4. Algorithms for Surface Modelling

There are many approximation approaches for surface modeling based on 3D scattered points, including a polygonal model (e.g., a mesh by interpolation) or a regression model (e.g., a polynomial or B-spline surface) [30,31,32]. The difference of the concrete level among the gaps is typically not too significant owing to uniform casting and the concrete’s fluidity. Among these methods utilized in various applications for fitting point cloud data, the polynomial fitting is usually employed to smooth and regular objects due to its simple operation and function of global optimization [30].

1.5. Structure of the Contribution

The contribution is organized as follows. Section 2 elaborates the monitoring concept and the proposed data processing methods, and Section 3 describes the quality evaluation metrics for surface modeling and sphere detection. Experimental results are presented in Section 4. Further discussions, including comparative study, error analysis, and limitations, are provided in Section 5, followed by the conclusions and outlooks in Section 6.

2. Theories and Methods

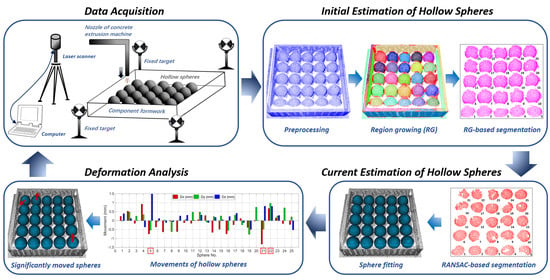
2.1. Monitoring Concept and Overview of the Processed Method

For the monitoring of hollow spheres and the concrete level during component production, a monitoring concept was designed for point cloud data acquisition as shown in Figure 2. One laser scanner is set up on the stable ground and close to the component area, and it is fixed on a single station throughout the monitoring process so that the uncertainty of data registration from multi-station measuring could be avoided. By a network connection to a computer, the scanner can be controlled and transmit data in real-time. Four or more laser scanner targets are supposed to be fixed around the formwork and kept stationary as the georeferencing. The scanning range of horizontal angle ${\theta }_{Hor}$ must cover the whole component formwork and all fixed targets. Additionally, the scanner should be mounted as high as possible to ensure that all hollow spheres and the surface of fresh concrete in the formwork can be scanned without a large area of occlusion.

The flowchart of the proposed method for monitoring hollow spheres and concrete level is shown in Figure 3. According to the order of scanning, the whole process is composed of two main parts.

The first part is to estimate the initial parameters of hollow spheres based on the first scanning (before casting process) as shown in the left rectangle, and this part is defined as the first epoch (epoch means a time period defined to be monitored). Taking the preprocessed point cloud data as the input, a preliminary segmentation and clustering of spherical objects, including RG and the extraction of the spherical clusters, are performed to acquire the point clouds of hollow spheres. Then, fine segmentation of spheres using RANSAC is conducted. Finally, the initial center position and the radius of each sphere are estimated by least squares (LS) under a rigorous Gauss–Helmert model.

The second part involves the estimation of the hollow spheres and the concrete level in current epochs as shown in the right rectangle. At first, the range of region of interest (ROI) for spheres is determined according to the current height of the concrete level. Then the ROI of each sphere and concrete level are selected with an adaptive range. The combination of statistical outlier removal (SOR) and RANSAC-based segmentation is used to obtain the point set of the exposed spherical surface in each ROI. While the representative point (RP) of each gap between adjacent spheres is calculated to build the point set of the current fresh concrete surface. Finally, LS and cubic polynomial fitting (CPF) are adopted to fit the hollow spheres and concrete level respectively based on the corresponding point sets. After the first scanning, the radius of each sphere is fixed as a constant in sphere fitting by using the estimation from the first epoch.

The advantage of the first part is that the prior information is not needed with respect to approximate positions of spheres. Due to the significant time consumption of RG and spherical cluster extraction, however, RG-based segmentation should only be used before concrete casting. For the subsequent scanning, with the initial positions and the estimated radii, the selection of ROI can be performed to get the local area of each sphere as the input dataset of RANSAC-based segmentation. The range of ROI for each sphere depends on the height of the current concrete level, enabling the ROI to cover the whole exposed spherical part in any case under a high inlier proportion. It is also optional to update the positions of spheres based on the current-epoch results to select the ROI in the next epoch. In sequence, the different steps of the proposed method are described in detail.

2.2. Data Preprocessing

2.2.1. Georeferencing

Since the scanner must keep both position and orientation fixed on one station, a stable georeferencing based on the local coordinate system of the scanner ought to be guaranteed during the whole process. After the scanning of each epoch, the position of each fixed target will be compared to its initial center coordinates. If the locations of all targets change within the measurement accuracy, the position and orientation of the scanner can be deemed to be stationary. Otherwise, it is possible to recover the reference frame by Helmert transformation [33].

2.2.2. Selection of the Object Region and Downsampling

The original point cloud data usually includes redundant parts or points due to the setting of a large scanning range or a high resolution. In order to efficiently reduce the computing time and memory usage, the original point cloud is clipped by the boundary of a polygonal prism that can cover the whole object region and downsampled.

Compared with other downsampling techniques, the voxel grid filter has advantages of easy implementation, fast execution and uniform filtering [27,34,35]. The selection of voxel size will significantly influence the computational complexity and segmentation effect [36]. Theoretically, the smaller the sphere radius is, the smaller the voxel size should be set, so as to ensure enough points for the calculation of the normal vector and curvature and enough inliers for RANSAC-based segmentation. Considering the appropriate point density for sphere detection and overall computational efficiency, 3 × 3 × 3 mm³ voxel grid is experimentally determined for the downsampling for spheres with a radius of 74 mm.

2.2.3. Outlier Removal

The outliers occur in point cloud data due to occlusions or sensor imperfections, which can cause geometrical discontinuities and arbitrary surface shapes with sharp features inevitably [37,38,39]. Considering that the outlier removal will be performed repeatedly in the point cloud processing of this monitoring work, a concise and highly-efficient method called statistical outlier removal filtering is adopted [40]. The critical parameters of SOR filtering are k (the number of k-nearest neighbors) and m (the multiple of standard deviation). In particular, k controls the size of the recognized outlier cluster, while m determines the proportion of filtered points (e.g., about 2.3% points are deemed as outliers when m = 2.0). k was set to 30 empirically herein, and it can be set higher if the isolated outlier clusters with more points are expected to be removed.

2.3. Surface Modeling of Concrete Level

After each layer of casting, the height of the concrete level in the formwork is supposed to be estimated in order to acquire the current distribution of the fresh concrete. Besides, the geometric information on the concrete level is needed for the ROI selection of hollow spheres. However, not all areas of the concrete level can be scanned due to occlusion. Therefore, a surface model can be established from limited points on the concrete surface to approximate the actual concrete level. This step consists of the ROI selection of the concrete level and surface fitting.

2.3.1. Selection of Points on the Concrete Level

Surface points of the concrete level (PoCL) can only be detected in the gap between several adjacent spheres, even though the surface will rise and change during casting. This contribution merely focuses on the component simply including equal-radius spheres. According to [5], there are two dense packing patterns for these identical spheres in one plane: in cubic-primitive packing (orthogonal pattern) four spheres are touching each other in one point (see Figure 4b), leading to a maximum in mass savings of 52%, and in hexagonal-primitive packing (hexagonal pattern) three spheres are touching each other in one point (see Figure 4c), which leads to a maximum in mass savings of 60%. For both patterns, the gap area where PoCL is located can be determined by the geometric relation between three touching (nearest) spheres in one packing unit, as illustrated in Figure 4. Accordingly, it is possible to determine these gaps after obtaining the position of every sphere (see Section 2.4 and Section 2.5).

A method to define the ROI for the concrete level to represent the gap area is proposed in this contribution. The center of each ROI coincides with the center of its corresponding gap. Based on the initial or current positions of spheres, a local selection can be made for the ROI including PoCL. To reduce the time consumption when selecting a circular area (due to numerous distance calculations), a small square area among three or four adjacent spheres is selected as the ROI for the concrete level, as shown in Figure 4. The geometric property of this ROI is that the horizontal distances between the ROI’s center and each sphere’s center are just equal if these spheres have an identical radius. That means the center of ROI is the center of the circumcircle of the triangle, which is constructed by the center points of three adjacent spheres, and this point is also the intersection of perpendicular bisectors of the three sides of the triangle. For implementation, thus, only the circumcircle’s center needs to be calculated based on the centers of three adjacent spheres found via the nearest neighbor search. The central position of ROI $(x_{\mathrm{ROI}}, y_{\mathrm{ROI}})$ can be calculated by

$$\begin{array}{l}{x}_{\mathrm{ROI}}=\frac{(y_2-y_1)(x_3^2+y_3^2-x_2^2-y_2^2)-(y_3-y_2)(x_2^2+y_2^2-x_1^2-y_1^2)}{2(y_2-y_1)(x_3-x_2)-2(y_3-y_2)(x_2-x_1)}\hfill \\ y_{\mathrm{ROI}}=\frac{(x_3-x_2)(x_2^2+y_2^2-x_1^2-y_1^2)-(x_2-x_1)(x_3^2+y_3^2-x_2^2-y_2^2)}{2(y_2-y_1)(x_3-x_2)-2(y_3-y_2)(x_2-x_1)}\hfill \end{array},$$

(1)

where $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ are the horizontal positions of the three adjacent spheres around one gap. The scale of ROI should be smaller than the gap’s area when the concrete surface and the height of sphere centers are at the same level (the smallest area of concrete level). Based on the geometric relations in Figure 4b,c, 0.58-times radius for cubic-primitive packing and 0.21-times radius for hexagonal-primitive packing are calculated as the side length of the ROI.

2.3.2. Representative Point of Each Gap

On the one hand, the placement errors or unequal radius (due to manufacturing errors from submillimeter to several millimeters) of spheres may result in the inconsistency between the ROI’s center and the gap’s center, and this deviation will possibly cause the ROI to include some outliers like the points on spheres. On the other hand, these PoCL in a gap are theoretically at the same height because of the fresh concrete’s flowability, hence it is not necessary to use all PoCL in one gap to reconstruct the concrete surface.

To simplify the calculation and improve the robustness, only the point with the median height is taken as the representative point for each gap. This method can not only eliminate the influence of outliers, but also make the distribution of fitting points more uniform on the fitted surface.

2.3.3. Surface Modeling Using Cubic Polynomial Fitting

Different-order polynomials perform differently in terms of the number of coefficients and the fitting accuracy [30]. In this contribution, considering the model performance and computing time, a cubic (three-order) polynomial fitting (CPF) algorithm is adopted to model the surface of the concrete. Its function model can be written as

$$z=a_0+a_{1}x+a_{2}y+a_3{x}^2+a_4{y}^2+a_{5}xy+a_6{x}^{2}y+a_{7}x{y}^2+a_8{x}^3+a_9{y}^3,$$

(2)

where $(x, y, z)$ are the coordinates of the representative point and $a_i( i=0, 1, \dots , 9)$ are the polynomial coefficients. To determine the ten coefficients in Equation (2), at least ten points are needed. According to the model of indirect adjustment, the observation equation can be written as

$$\underset{V}{\underbrace{\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]}}=\underset{A}{\underbrace{\left[\begin{array}{cccccccccc}1& x_1& y_1& x_1{}^2& y_1{}^2& x_1{y}_1& x_1{}^2{y}_1& x_1{y}_1{}^2& x_1^3& y_1^3\\ 1& x_2& y_2& x_2^2& y_2^2& x_2{y}_2& x_2^2{y}_2& x_2{y}_2{}^2& x_2^3& y_2^3\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_n& y_n& x_n^2& y_n^2& x_n{y}_n& x_n^2{y}_n& x_n{y}_n^2& x_n^3& y_n^3\end{array}\right]}} \underset{\widehat{X}}{\underbrace{ \left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_9\end{array}\right]}}-\underset{L}{\underbrace{\left[\begin{array}{c}{z}_1\\ z_2\\ ⋮\\ z_n\end{array}\right]}},$$

(3)

where $n$ is the number of observations (representative points), $V$ is the improvement vector (or error vector), $A$ is the design matrix, $L$ is the observation vector, and $\widehat{X}$ is the parameter to be estimated. Based on the LS, the optimal solution of the parameters (polynomial coefficients) is given in Equation (4), where the weight matrix $P$ is regarded as an identity matrix here. The standard deviation (Std.) ${\widehat{\sigma }}_0$ of the surface fitting can be calculated by Equation (5) with u = 10 (for ten coefficients to be estimated).

$$\widehat{X}={(A^{T}PA )}^{-1}{A}^{T}PL$$

(4)

$${\widehat{\sigma }}_0=\sqrt{\frac{V^{T}PV}{n-u}}$$

(5)

2.4. Initial State Estimation of Hollow Spheres

As stated in Section 2.1, the initial positions and radii of hollow spheres are supposed to be estimated after the first scanning (before casting) if there is no prior information of sphere parameters. This part consists of preliminary segmentation and spherical cluster extraction, and the parameters of spheres can be estimated by LS after further RANSAC-based segmentation (see Section 2.5.2).

2.4.1. Preliminary Segmentation Using 3D Region Growing

The 3D RG typically starts from one or more points (seed points) featuring specific characteristics and then gathers the nearest neighbors in the seed area on the basis of certain constraints such as similar surface orientations or curvatures [26]. Constraints of surface normal vectors and curvatures were widely used to find the smoothly connected areas that would be clustered as specific regions [23,25,41,42]. The detailed process of the 3D RG algorithm adopted in this work is described in [23,25]. Vo et al. [27] found that the method requires a considerable amount of time for parameter tuning, especially for curved surface or sphere segmentation.

The influence factors in the standard 3D RG algorithm include the neighborhood size for normal vector and curvature estimation, the threshold of angle difference (TAD) between normal vectors of each nearest neighbor point and current seed point, the threshold of local curvature (TLC) for each point, the neighborhood size for RG searching, and the threshold of point number as a clustered region, etc. There are two ways to define the size of neighborhood: the point number of k-nearest neighbors or the radius of the nearest neighbor (RNN). Herein, RNN is adopted to calculate the normal vector, local curvature and growing neighborhood, which enables an optimal neighborhood under different point densities.

In this contribution, principal component analysis (PCA) is applied to estimate the normal vector and curvature of each point (cf. [43,44]). In consideration of the computational complexity and the insensitivity to the noise, the ratio between the smallest eigenvalue and the sum of eigenvalues (derived from the covariance matrix of the neighboring point set for the query point) is used to approximate the surface variation, and to indicate the local curvature around the query point indirectly [43].

To verify the feasibility of 3D RG algorithm for multiple sphere segmentation and to investigate the optimal selection of critical parameters, a setup of eight plastic spheres with a radius of 74 mm was used to simulate the layout of hollow spheres. Figure 5 shows the placement of spheres and the point cloud of this setup. Part of the background was retained to show the process of the sphere being detected from a complex scenario.

The calculations of normal vector and curvature for each point are the basis of the RG-based segmentation, while the size of the corresponding neighborhood will influence the PCA-based normal estimation directly. Figure 6 shows part of the segmentation results under different normal and curvature calculations, where RNN was set to different sizes (from 10 mm to 50 mm) while other parameters are fixed with empirical values. The segmented clusters are labeled with random colors, and the red parts are not considered as a cluster because of too few points (less than the minimum point number as a region). The bad or wrong segmentations are marked by black dotted rectangles according to the visual comparison with the ground truth.

Figure 6 shows that smaller neighborhood selection caused over-segmentation (see Figure 6a) while a large RNN setting led to under-segmentation (see Figure 6c). For this multiple-sphere test, the optimal RNN is empirically from 20 mm to 30 mm according to the segmentation effects within the investigated range of RNN.

In addition to the neighborhood size in normal and curvature calculations, TAD and TLC also influence the effect of 3D RG-based segmentation. Figure 7 and Figure 8 show part of segmentation results under different settings of TAD (from 2.00° to 4.00°) and TLC (from 0.01 to 20.0).

Figure 7 indicates that the segmentation result was sensitive to the change of TAD. Similar to the results under different RNN, a small TAD setting caused over-segmentation on the spheres (see Figure 7a), while a large TAD setting led to under-segmentation to a certain extent (see Figure 7c). If only concerning whether the spherical points can be segmented independently and completely, the range from 2.75° to 3.75° of TAD is suggested for the sphere with the given radius.

Compared to TAD, TLC has not such a significant influence on the segmentation effects (see Figure 8). For a TLC between 0.05 and 10, all obvious geometric primitives could be segmented and clustered almost perfectly. There was a slight under-segmentation when TLC reached 20 (see Figure 8c). This is because TLC only determines the generation of seed points rather than region points, while the clustering of region points depends on TAD merely. However, too small TLC may hinder the generation of seed points and stop the process of region growing in the large-curvature regions, like edges and spheres. These regions would be independently clustered from the point cloud and were labeled as red due to less points to be treated as a cluster (see Figure 8a), which caused discontinuity on the spherical surfaces. Therefore, TLC from 0.05 to 10 is suggested for this scanning test. As for the point number of the searching neighborhood for 3D RG, an empirical value from 10 to 30 is chosen taking into account the point density, since the result of RG is also not sensitive to this parameter.

2.4.2. Screening Conditions for Spherical Clusters

Spherical clusters are supposed to be extracted from the preliminary segmentation results completely and quickly. In this contribution, two simple screening conditions based on the spatial ranges and the medians of sorted curvatures of segmented clusters are proposed to extract the spherical clusters from RG-based segmentation. The extraction steps can be summarized as follows:

• The spatial ranges in the direction of three axes of each cluster whose number of points is greater than a threshold will be calculated.
• The curvature of each cluster within the threshold of spatial ranges (TSR) will be calculated and sorted.
• The cluster of which the median of sorted curvatures is within a specific threshold (TCM) will be regarded as a sphere and extracted into the dataset storing spherical points.

The determination of TSR ought to refer to the radius of the sphere and the proportion of visible part. When scanning with a single station, normally less than 50% of the surface of a sphere is exposed, and it may be even less under the occlusion of other spheres. Considering the radius of these spheres is 74 mm in this multiple-sphere scanning test, the range of TSR is set from 0.05 m to 0.16 m in the direction of X and Y axes and from 0.02 m to 0.16 m in the direction of Z-axis empirically.

The curvature estimations of spherical clusters may be not consistent because of the errors at some edge points. Figure 9 shows the curvature distributions of two extracted spherical clusters in the scanning test (results of other spheres are offered in Figure A1 in Appendix A). The mean and median of point curvatures are also displayed. The average curvatures of these spherical clusters are between 0.014 to 0.017, while the median is slightly higher than the mean of curvatures. To weaken the influence of outlier curvatures at some edge points and make a more stable threshold setting, the median of sorted curvatures of a cluster is adopted as the second screening condition for the extraction of spherical clusters. According to Figure 9, the range of TCM was set from 0.014 to 0.018 in this scanning test.

The extracted spherical clusters from the RG-based segmentation result by the two screening conditions are shown in Figure 10. These eight spheres were extracted from the segmented point cloud respectively and completely. However, these spherical clusters may still contain some outliers or noise which could be further eliminated by RANSAC-based segmentation (see Section 2.5.2). Then the center coordinates and radii of spheres are estimated by LS fitting (see Section 2.5.3) after obtaining the finely segmented spherical points. In addition, for an unorganized point cloud, the extracted clusters will be sorted by their number of points in RG-based segmentation, resulting in that the actual sequences are disordered in the horizontal direction. It is thus crucial to reorder these spherical clusters according to their center positions and number these spheres in accordance with the X-axis or Y-axis direction.

2.5. Current State Estimation of Hollow Spheres

Owing to the dense packing of the hollow spheres, their horizontal movements would normally be in a small extent during the casting process. Therefore, it is possible to estimate the current state of a hollow sphere within a limited horizontal range (i.e., ROI). In this case, the sphere can be segmented by RANSAC with fewer iterations under a higher proportion of spherical points (inliers) in a ROI. Moreover, the time consumption is significantly less than that of RG-based segmentation, which enables timely feedback during the production process. Thus, this RANSAC-based segmentation is adopted to estimate the current positions of the hollow spheres after the first epoch.

2.5.1. Selection of Regions Including Spheres

Since the standard RANSAC algorithm typically segments a single object, the input dataset should only contain one sphere, and the proportion of inliers ought to be as high as possible. Based on the initial position and the radius estimated from the first epoch, it is possible to select a local area as the ROI including one single sphere. Supposing that the horizontal movement of each sphere is within the range of 0.3-times radius, the region with a range of 1.3-times radius from the center of each sphere should be selected as the ROI. A horizontal square area of which sides are along the X-axis and Y-axis direction is selected as the ROI for each sphere, as demonstrated in Figure 11. These ROIs are merely determined by the center position and side length, and half of the side length is defined as the range of ROI.

The center position of any ROI is entirely consistent with its corresponding spheres, and they can be acquired from the initial state estimation and updated by the current state estimations (when the horizontal movement tends to be significant). In order to ensure that ROI can completely cover the sphere and maintain a high inlier proportion as well, the range of ROI can be set by

$$R_{\mathrm{ROI}}=\{\begin{array}{l}1.3\cdot RH\le R\hfill \\ \sqrt{R^2-{(H-R)}^2}+ 0.3\cdot RH>R\hfill \end{array},$$

(6)

where $R_{\mathrm{ROI}}$ is the range of ROI after each casting, $R$ is the radius of the sphere and $H$ is the current height of the concrete level from the bottom of the sphere. $H$ can be obtained from the surface modeling of concrete level, i.e., the height of the fitted surface at the position of sphere center by Equation (2). Equation (6) makes the selection of ROI more adaptive and ensures the inlier ratio accordingly with the decrease of the sphere’s exposed part. Figure 12 shows the ROI for each sphere ($R_{\mathrm{ROI}}$ is 1.3-times radius) in the multiple-sphere scanning test.

2.5.2. Sphere Segmentation Using RANSAC

As an efficient and robust method of model segmentation from the dataset with a high amount of noise and outliers, RANSAC can be performed in each ROI to segment the included sphere. The descendants of RANSAC (e.g., least median of squares (LMEDS), randomized RANSAC (RRANSAC), progressive sample consensus (PROSAC), etc.) are able to promote the robustness and efficiency to a certain extent, limitations or imperfections still exist in specific cases [45]. Considering the comprehensive performance on computing time and robustness, standard RANSAC of which detailed paradigm is given in [29] is employed for the segmentation of hollow spheres herein. Taking into account the accuracy and density of the point cloud as well as the size of the spheres, 2 mm was empirically set as the distance threshold (DT) between the inlier point and the estimated model in RANSAC method.

In order to eliminate the points that do not belong to the target sphere and further improve the proportion of inlier, the SOR filter is used to preprocess the point cloud in each ROI before segmentation.

2.5.3. Sphere Fitting and Parameter Estimation

Sphere fitting is the process of estimating the center coordinate and radius of each sphere based on a certain number of spherical points. A sphere in the Cartesian coordinate system can be described as Equation (7) by its center point $(x_c, y_c, z_c)$ and radius $r$.

$$r^2={(x_i-x_c)}^2+{(y_i-y_c)}^2+{(z_i-z_c)}^2,$$

(7)

where $(x_i, y_i, z_i)$ with $i=1, 2, \dots , n$ are the coordinates of observed points on the sphere. Considering the measurement errors, the improvements $V={[v_{x_i} \dots v_{y_i} \dots v_{z_i}]}^T$ are introduced for the observation vector $L={[x_1 y_1 z_1 x_2 y_2 z_2\dots x_n y_n z_n]}^T$, thus the nonlinear observation equation can be written as

$$Y_i(L+V,X)={(x_i+v_{x_i}-x_c)}^2+{(y_i+v_{y_i}-y_c)}^2+{(z_i+v_{z_i}-z_c)}^2-r^2.$$

(8)

Equation (8) can be linearized and solved by Gauss–Helmert model in an iterative process [46]. The initial approximate parameters ${\widehat{X}}^o$ could be determined by solving the linear Equation (9) which regards $x_c$, $y_c$, $z_c$, and $r^2-x_c^2-y_c^2-z_c^2$ as the parameters. The optimal estimation of the parametric vector is given in Equation (4) based on the linear LS [47], then the initial parameter ${\widehat{X}}^o={[x_c^o y_c^o z_c^o r^o]}^T$ will be easily obtained. The initial improvements $V^o$ can be zero vector.

$$\underset{V}{\underbrace{\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]}}=\underset{A}{\underbrace{\left[\begin{array}{cccc}2x_1& 2y_1& 2z_1& 1\\ 2x_2& 2y_2& 2z_2& 1\\ ⋮& ⋮& ⋮& ⋮\\ 2x_n& 2y_n& 2z_n& 1\end{array}\right]}} \underset{\widehat{X}}{\underbrace{ \left[\begin{array}{c}{x}_c^o\\ y_c^o\\ z_c^o\\ r^o{}^2-x_c^o{}^2-y_c^o{}^2-z_c^o{}^2\end{array}\right]}}-\underset{L}{\underbrace{\left[\begin{array}{c}{x}_1^2+y_1^2+z_1^2\\ x_2^2+y_2^2+z_2^2\\ ⋮\\ x_n^2+y_n^2+z_n^2\end{array}\right]}}.$$

(9)

In the adjustment process of the Gauss–Helmert model, the model matrices $A$ and $B$ arise after the linearization of Equation (8) and are denoted as follows:

$$A(V,X)={\left({\frac{\partial Y_i}{\partial X}|}_{L_i+v_i^o,X^o}\right)}_{n\times 4}=-2\cdot \left[\begin{array}{cccc}{x}_1+v_{x_1}^o-x_c^o& y_1+v_{y_1}^o-y_c^o& z_1+v_{z_1}^o-z_c^o& r^o\\ x_2+v_{x_2}^o-x_c^o& y_2+v_{y_2}^o-y_c^o& z_2+v_{z_2}^o-z_c^o& r^o\\ ⋮& ⋮& ⋮& ⋮\\ x_n+v_{x_n}^o-x_c^o& y_n+v_{y_n}^o-z_c^o& z_n+v_{z_n}^o-z_c^o& r^o\end{array}\right]$$

(10)

$$B(V,X)={\left({\frac{\partial Y_i}{\partial V}|}_{L_i+v_i^o,X^o}\right)}_{n\times 3n}=2\cdot \left[\begin{array}{ccc} diag(x_i+v_{x_i}^o-x_c^o)& diag(y_i+v_{y_i}^o-y_c^o)& diag(z_i+v_{z_i}^o-z_c^o)\end{array}\right]$$

(11)

Then, the observation equation will be linearized and written as

$$\Delta Y_i(V,X)=A\widehat{x}+BV+w=0,$$

(12)

where $\widehat{x}=\widehat{X}-X^o$, $w=-B{V}^o+Y(V^o,X^o)$. At each iteration, the solution of the increment of the parameters $\widehat{x}$ and the improvements $V$ are as follows, where $Q_L$ is the cofactor matrix of the observations. Then, the current estimated parameters $\widehat{X}$ are obtained from Equation (15) and used to update the approximate parameters $X^o$ while $V^o$ is updated by Equation (14) directly after each iteration until $\Vert \Delta \widehat{x}\Vert$ is less than the selected accuracy limit (e.g., 10⁻⁶ m).

$$\widehat{x}=- {(A^T{(B{Q}_L{B}^T)}^{-1}A)}^{-1}{A}^T{(B{Q}_L{B}^T)}^{-1}w$$

(13)

$$V=- Q_L{B}^T{(B{Q}_L{B}^T)}^{-1}(A\widehat{x}+w)$$

(14)

$$\widehat{X}=X^o+\widehat{x}$$

(15)

The fitting errors of the estimated sphere center (${\sigma }_{x_c}, {\sigma }_{y_c}, {\sigma }_{z_c}$) and the radius (${\sigma }_r$) are listed in Equation (16) where the square root of the posteriori variance factor ${\widehat{\sigma }}_0$ can be calculated by Equation (5) with u = 4. $Q_{\widehat{X}}={(A^T{(B{Q}_L{B}^T)}^{-1}A)}^{-1}$ is the cofactor matrix of the estimated parameters.

$$\begin{array}{cccc}{\sigma }_{x_c}={\widehat{\sigma }}_0\sqrt{Q_{\widehat{X}(1,1)}},& {\sigma }_{y_c}={\widehat{\sigma }}_0\sqrt{Q_{\widehat{X}(2,2)}},& {\sigma }_{z_c}={\widehat{\sigma }}_0\sqrt{Q_{\widehat{X}(3,3)}},& {\sigma }_r={\widehat{\sigma }}_0\sqrt{Q_{\widehat{X}(4,4)}}\end{array}$$

(16)

In this monitoring case, a precise radius of each sphere derived from the initial parameter estimation before casting can be utilized in the subsequent epochs, considering the sizes of the hollow spheres will not change during the production process. This would mean that the radius $r$ can be set to a constant and the parametric vector only contains the center coordinates of spheres (${\widehat{X}}^{\prime }={[x_c y_c z_c ]}^T$) after the first epoch. In this way, the Jacobian matrix $A$ will be in the form of Equation (17), while the iterative process remains the same as above.

$$A={\left({\frac{\partial Y_i}{\partial X^{\prime }}|}_{L_i+v_i^o,X^o}\right)}_{n\times 3}=-2\cdot \left[\begin{array}{ccc}{x}_1+v_{x_1}^o-x_c^o& y_1+v_{y_1}^o-y_c^o& z_1+v_{z_1}^o-z_c^o\\ x_2+v_{x_2}^o-x_c^o& y_2+v_{y_2}^o-y_c^o& z_2+v_{z_2}^o-z_c^o\\ ⋮& ⋮& ⋮\\ x_n+v_{x_n}^o-x_c^o& y_n+v_{y_n}^o-z_c^o& z_n+v_{z_n}^o-z_c^o\end{array}\right]$$

(17)

2.6. Deformation Analysis of Hollow Spheres

The deformation analysis in this contribution only refers to the movement of the sphere (i.e., the displacement of the sphere center), not including the change of the sphere shape. Based on the estimated parameters from sphere fitting, the deformation of a hollow sphere in epoch-i ($D_i$) is defined as the change of its center coordinates compared to the first epoch (epoch-1):

$$D_i={[D_{X, i} D_{Y, i} D_{Z, i}]}^T={\widehat{X}}_{epoch\_i}-{\widehat{X}}_{epoch\_1}={[x_{c,i}-x_{c,1} y_{c,i}-y_{c,1} z_{c,i}-z_{c,1}]}^T.$$

(18)

To verify the significance of the deformations, the statistical hypothesis testing should be performed on the results. Herein, the test quantity for localizing the sphere movements is defined as

$$F_{epoch\_i}=\frac{D_i^T{\Sigma }_{D,i}^{-1} D_i}{p}=\frac{D_i^T{(s_0^2\cdot Q_{D, i}+{\Sigma }_{georef})}^{-1}{D}_i}{p},$$

(19)

where $p$ is the dimension of the sphere center (i.e., $p=3$), ${\Sigma }_{D, i}$ is the variance-covariance matrix of deformations which also considers the variance of georeferencing ${\Sigma }_{georef}$ (equal to the root mean square (RMS) of the deviation of the control measurements to the fixed targets after each epoch), $s_0^2=\frac{V_1{}^T{Q}_{L,1}^{-1}{V}_1+V_i{}^T{Q}_{L,i}^{-1}{V}_i}{f_1+f_i}$ ($V_1$, $V_i$ and $f_1$, $f_i$ are the fitting residuals and the degrees of freedom respectively in epoch-1 and epoch-i) and the cofactor matrix $Q_{D,i}=Q_{\widehat{X},1}+Q_{\widehat{X},i}$.

Assuming the zero-hypothesis is that the sphere in epoch-i did not move compared to epoch-1, then a significant deformation of the sphere will be detected statistically at the significance level of $\alpha$ when the test quantity is larger than the corresponding reference value ($F_{p,f_i,1-\alpha }$) in the F-distribution.

3. Quality Evaluation

Since the number of RP is merely relevant to the number of hollow spheres rather than the point cloud, only a small number of RP are involved in the CPF-based surface modeling. Thus, the computing time of the surface modeling part is millisecond-level, which does not play a role in the whole data processing time. To evaluate the accuracy of surface modeling, check points (CP) can be selected from the actual concrete level in the original point cloud after casting, then the modeling error at CP (E_CP) can be calculated by

$$E_{\mathrm{CP}}=\left| H_{\mathrm{CP}}-Z \right|,$$

(20)

where $H_{\mathrm{CP}}$ is the actual height of CP and Z is the estimated height from the surface model by Equation (2). Moreover, the standard deviation (Std.) of the surface fitting from Equation (5) are adopted to evaluate the modeling accuracy as well.

To assess the performance of the proposed method for multiple sphere detection, a quality evaluation metric for engineering geodesy processes developed by IIGS (cf. [48,49]) is adopted in this contribution. Three characteristics in this quality model to describe the product-oriented quality are used here: completeness (Com), accuracy (Acc), and real-time capability (RtC).

Herein, these characteristics are substantiated by specific parameters respectively. Com is defined by the ratio of detected spheres with respect to the total sphere number, and it reflects the quality of the segmentation process.

Acc is quantified by the average/maximum position errors of sphere fitting. The position error (${\sigma }_P$) of each fitted sphere can be calculated by

$${\sigma }_P=\sqrt{{\sigma }_{x_c}{}^2+{\sigma }_{y_c}{}^2+{\sigma }_{z_c}{}^2},$$

(21)

where the standard deviations of the estimated sphere center (${\sigma }_{x_c}, {\sigma }_{y_c}, {\sigma }_{z_c}$) can be acquired from Equation (16). Then, Acc is denoted by the average ${\sigma }_P$ and maximum ${\sigma }_P$ of the detected spheres.

RtC is parameterized as the time consumption of the acquisition and processing of the point cloud data. The time of point cloud acquisition depends essentially on the performance of the scanner, the range of target area, and the scanning settings of resolution and quality. Here, only the computing time of the sphere detection and estimation is considered for the evaluation of RtC.

4. Experiments and Results

An experiment was conducted to verify and evaluate the proposed methods for monitoring the production process of meso-graded concrete components, and to make a deformation analysis for the hollow spheres during production. The center position and radius of each sphere were acquired as reference values by manually selecting the spherical points from the original point cloud and making an optimal estimation in a commercial software called Geomagic Studio [50].

4.1. Experiment Description

In this experiment, the production of a small-scale meso-graded concrete component was monitored in the laboratory of ILEK. The monitoring configuration and casting process are shown in Figure 13. 25 spheres with a designed radius of 50 mm were placed in an orthogonal packing pattern within the formwork. Leica HDS7000 laser scanner was set up on a tripod about 2 m away from the formwork. Four black and white planar targets were set around the working area for georeferencing. Owing to the indoor environment and short measuring distance, the influence of atmospheric variation on the measurement is negligible. The sample was produced manually by casting a defined amount of liquid fresh concrete into the gaps between the hollow spheres. As a result of the manual production, the surface of some hollow spheres was partially obstructed with concrete (see Figure 13e,f). However, these unintentional imperfections allow to improve and evaluate the robustness of the sphere detection method against such outliers.

There were four epochs of scanning during the monitoring process. Epoch-1 was the first scanning to estimate the initial center position and the radius of each sphere before casting, thus the initial parameters of spheres were estimated and compared to the reference values in epoch-1, while the movements of hollow spheres and the concrete level were monitored from epoch-2 to epoch-4.

The relevant algorithms were implemented based on Point Cloud Library (PCL) [51] and Microsoft Visual Studio development platform. All data processing in this experiment was performed on a 2.80 GHz Intel Core i7-7700 processor and 8.0 GB of RAM.

4.2. Data Acquisition and Preprocessed Data

The point cloud data acquisition consists of data transmission and format conversion. To obtain unified-format point cloud data in real-time, an independent program with a user interface for the HDS7000 laser scanner was developed based on the corresponding software developer kits (SDK). The scanner can be controlled to scan the objects with predetermined angle range, resolution and quality. In this experiment, the scanning process in each epoch took about 2 min with a high-resolution setting and 90° horizontal scanning range (to cover the target area) in the scanner. The point cloud data will finally be stored in PCD format by the format conversion module.

During the experiment, the scanner was fixed in one station. Georeferencing was performed in each epoch to check the stability of the scanner, and the changes of fixed targets were calculated to correct the point cloud. Using the voxel grid filter with 3 × 3 × 3 mm³ grid size and SOR filter with the threshold of double standard deviation, the preprocessed point clouds of component areas were obtained as shown in Figure 14, followed by the detailed descriptions in

Table 1. Descriptions of the preprocessed point clouds.

Description	Epoch-1	Epoch-2	Epoch-3	Epoch-4
Number of Points	64,711	65,081	64,825	62,305
Average Point Spacing	2.31 mm	2.29 mm	2.28 mm	2.23 mm
Size of Selected Area	600 × 600 × 200 mm3

.

4.3. Experimental Results

Figure 15 presents the sphere segmentation for initial parameter estimation in the first epoch based on the combination of RG and RANSAC. According to the parameter tuning described in Section 2.4, the optimal parameters of TAD, TSR, and TCM were obtained and listed in

Table 2. The parameter settings in the experiment.

RNN	TAD	TLC	TSR	TCM	DT
20 mm	4.0°	0.5	Horizontal: 0.02~0.12 m	0.025~0.035	2 mm
			Vertical: 0.02~0.12 m

. The errors of estimated position (E_X, E_Y, E_Z) and radius (E_R) of each sphere by comparing with the reference values from Geomagic Studio are given in Figure 16. All errors are below 1 mm, and thus the initial positions and radii of spheres estimated in epoch-1 can be used for the following epochs.

In this experiment, to improve the robustness of sphere detection against the marked impact of outliers, the radius of each sphere was fixed as a geometric constraint in the sphere fitting process after the first epoch. Moreover, the limit of the maximum number of iterations in RANSAC was increased to get a more reliable estimation. The final segmentation and fitting results of the hollow spheres are offered in Figure 17.

The movement of each hollow sphere compared to epoch-1 was calculated by Equation (18) after getting the positions of sphere centers. To test whether these spheres were moved significantly or not, statistical hypothesis testing was conducted for each sphere by Section 2.6. The level of significance $\alpha$ was set to 0.3% in this experiment based on the 3-sigma rule, which means that the error probability of deformation analysis is 0.3%. The deformation (movement) results from epoch-2 to epoch-4 are shown in Figure 18, where the spheres with significant movements tested (with a 99.7% level of confidence) are marked on the X-axis with a red box.

The results in Figure 18 show that only one sphere moved below 1 mm in epoch-2 and no sphere moved in epoch-3 significantly. In epoch-4, three spheres moved within 1.5 mm in the three orthogonal directions. These movements are probably caused by the manual casting process in this experiment, which will be improved by an automatic casting procedure currently under development that utilizes a concrete extrusion machine. In any case, this level of movement of these spheres is so negligible that it will not affect the functionality of the component negatively. Therefore, this meso-graded concrete component was successfully produced in the experiment.

The quality evaluation of the sphere detection is shown in

Table 3. Quality evaluation of sphere detection.

Evaluation	Epoch-1	Epoch-2	Epoch-3	Epoch-4
Acc (avg/max) [mm]	0.18/0.42	0.12/0.21	0.14/0.23	0.22/0.63
Com [%]	100	100	100	100
RtC [s]	10.74	2.57	2.45	2.28

. All spheres were detected and estimated with submillimeter-level accuracy in this experiment. The computing time of sphere segmentation and fitting is closely related to the number of hollow spheres as well as the hardware configuration of the computer. Since the detection of hollow spheres is performed one by one, the processing time will increase linearly with the number and size of hollow spheres theoretically.

The surface modeling of the concrete level after each casting was also conducted in the experiment, as shown in Figure 19. Herein, 16 RPs of the corresponding 16 gaps among hollow spheres were obtained and used to build the fitting surface based on CPF. The absolute height of the formwork’s bottom was subtracted from the height of the modeled surface, hence the Z-value in Figure 19 is the relative height of the modeled surface from the bottom of the formwork.

The target levels of the cast concrete from epoch-2 to epoch-4 are 15 mm, 30 mm, 60 mm, while the average heights of the actual level according to the reconstructed surface model are 13 mm, 30 mm, and 71 mm in the three epochs, respectively. From Figure 19, it can be seen that the range of the height difference (along the Z-axis) between the actual casting level and the target level is from −6 mm to +2 mm in epoch-2, from −7 mm to +9 mm in epoch-3, and from +6 mm to +19 mm in epoch-4. These height differences also reflect the flatness of the actual concrete surface after casting.

In addition to the standard deviation (Std.) derived from the surface fitting by Equation (5), 16 CPs (located on the concrete level) were selected from the original point cloud to evaluate the modeling accuracy in each epoch by Equation (20). The related errors are listed in

Table 4. Quality evaluation of surface modeling.

Errors [mm]	Epoch-2	Epoch-3	Epoch-4
Std. of RP	1.81	3.43	4.59
max/min ECP *	4.32/1.21	5.73/0.92	6.28/1.58
average ECP *	2.48	4.02	4.97

* E_CP: the modeling error at the check point.

. The accuracy has reached millimeter-level in this experiment, while the increasing errors in the later epoch are mainly due to a limited number of RP that cannot represent all characteristic points of the actual concrete surface. Hence, the significant height difference to the target level in epoch-4 may be caused by the reduced accuracy of surface fitting or even by the manual casting process.

5. Discussion

5.1. Comparative Studies of Sphere Detection

The performance of the proposed method for multiple sphere detection from 3D point cloud is compared with two commonly used algorithms (eSphere in [15] and RansacSD in [18]). Although eSphere exhibits good performance with respect to the completeness, accuracy and robustness of sphere detection, the computing time is much longer than the other two methods due to its complexity (over 20 s for detecting 25 spheres in the experiment). Hence, the low RtC enables eSphere not applied to the sphere detection in the real-time monitoring of the large-scale concrete component production. RansacSD has developed the traditional RANSAC and enabled it to segment multiple models in one dataset [18]. However, the disadvantages of RansacSD are the sensitivity to parameter changes and the possible incompleteness of model detection, especially when the inlier ratio is small or excessive outliers are around models.

Table 5. Comparison of the sphere detection algorithms in the experiment.

Epoch	Method	Acc * (avg/max) [mm]	Com * [%]	RtC * [s]
Epoch-1	RansacSD [18]	0.21/0.42	100	5.86
	Proposed method	0.18/0.42	100	10.74
Epoch-2	RansacSD	0.14/0.25	100	6.02
	Proposed method	0.12/0.21	100	2.57
Epoch-3	RansacSD	0.17/0.35	100	5.88
	Proposed method	0.14/0.23	100	2.45
Epoch-4	RansacSD	0.37/0.62	92	5.52
	Proposed method	0.22/0.63	100	2.28

* Acc: accuracy; Com: completeness; RtC: real-time capability.

shows the performance comparison of RansacSD and the proposed method in this experiment. It can be seen that the completeness of RansacSD is only 92% in epoch-4 because Sphere-5 and Sphere-21 were not detected. Besides, the accuracy and real-time capability of RansacSD is inferior to the proposed methods from epoch-2 to epoch-4. However, RansacSD shows a better performance than the proposed method in the initial epoch in terms of the computing time. In general, the proposed method has superiorities in robustness and real-time capability compared to the other two methods.

5.2. Error Analysis of Sphere Detection

From the results of the experiment, the estimation errors of sphere parameters (by comparing with the reference values or calculated from the sphere fitting process) are all submillimeter-level, and they typically increase with the casting process (see Table 3). This is mainly because the corresponding spherical points (regarded as inliers) segmented from ROI are not all located on the hollow spheres or not enough to cover a whole sphere. The reasons for inaccurate or incomplete segmentation may be as follows:

• Insufficient spherical points or low point density: this can be caused by the gradual reduction of the exposed surface of spheres due to the increasing concrete layer, the mutual occlusion between spheres, the improper distance and scanning angle between the concrete component and the scanner, etc.
• The interference of the fresh concrete sticking on the exposed surface of spheres after casting: this may lead to RANSAC classifying these outliers as inliers when there is a large obstruction area of exposed spheres by the concrete slurry. Too many outliers contained in the segmentation will result in wrong fitting results.

In the sphere fitting process, the spatial correlations between the observation points are neglected in the stochastic model and all spherical points are considered to be equally weighted. Hence, the variance–covariance matrix was simply defined as an identity matrix in this work. This may also affect the accuracy of sphere estimation to a certain degree.

Based on the error analysis above, the hollow sphere with a larger exposed surface in the scanning range and less disturbance by fresh concrete is easier to be detected and get a more accurate estimation. Hence, here are some suggestions to improve the monitoring performance:

• Setting up the scanner as high as possible to reduce the occlusion between the front and rear spheres and increase the exposed surface, and keeping the scanner close to the component to ensure a high data density.
• Reducing the range of ROI for hollow spheres manually to improve the proportion of inliers if the ratio of spherical points (inliers) in ROI is too low.

5.3. Limitations

The experimental results indicate that the completeness of sphere segmentation and the accuracy of sphere fitting may decrease with the rising concrete level. Thus, the proposed method exhibits limitations in terms of monitoring the spheres with a small, exposed surface. After some time for the respective layers, however, it is permissible that the gradually hardening concrete at the bottom can restrain the movements of spheres, if there is a sufficient adhesive bond between the fresh concrete and hollow spheres. The time-dependent adhesion and cohesion properties of the concrete can be specifically influenced by admixtures, thus enabling the control of the casting process. Therefore, the monitoring frequency for hollow spheres can be reduced after enough time for the bottom concrete to harden.

The spheres in this experiment have the same or quite similar radius. If the radii of the multiple spheres in the component were significantly different (as shown in Figure 1), however, the proposed method cannot recognize all spheres at once in the initial epoch. To solve this problem, the RG-based segmentation and spherical cluster extraction can be performed iteratively to extract spheres with different radii respectively. Each iteration with specific parameter settings can screen the spheres with a similar radius. In addition, the quantitative relationships between the parameter tuning and the sphere radius are not given in this contribution. This could be investigated thoroughly by sufficient tests on the spherical objects of different sizes in the future work.

6. Conclusions

A complete concept for monitoring the production process of meso-graded concrete components using TLS is proposed in this study, including automatic detection and estimation of the hollow spheres and surface modeling of the concrete level. The 3D point cloud data are acquired from the laser scanner in real-time and preprocessed to improve the data quality and availability. The efficient combination of RG and RANSAC algorithms is developed to segment the spherical points from the point cloud quickly after each scanning. The LS-based fitting method is used to estimate the position and radius of each hollow sphere, and deformation analysis is conducted to find the significantly moved spheres. The surface of the fresh concrete is modeled based on the sampling of representative points and cubic polynomial fitting.

The proposed methods are experimentally validated and evaluated, and the results show their good performance on automatic multiple-sphere detection and concrete surface modeling from point cloud data. During the production process of the exemplary meso-graded concrete component in this contribution, all hollow spheres were detected and estimated with submillimeter-level accuracy in a few seconds. A movement of 3–4 spheres was statistically detected, but this was insignificantly small for the load-bearing capacity of a concrete component. However, the questions of allowable tolerances for a component production process and how these can be integrated into the monitoring procedure arise. In addition to this research task, further work will involve investigating the quantitative relationship between the sphere size and parameter tuning in sphere segmentation. Besides, the spatial correlations and intensity information of the point cloud can be taken into consideration when building the stochastic model of TLS observations [52]. More adaptive downsampling algorithms [53] and optimized parallel processing [54] of multiple-sphere detection are possible for the production monitoring of large-scale graded concrete components integrated with hundreds of hollow spheres.