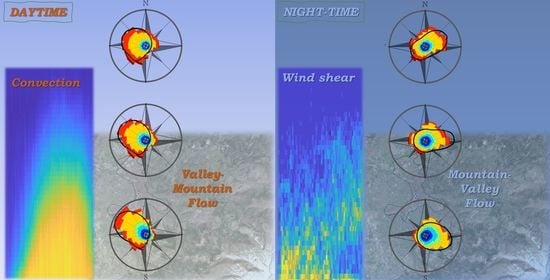
Wind and Turbulence Statistics in the Urban Boundary Layer over a Mountain–Valley System in Granada, Spain
Abstract
:1. Introduction
2. Experimental Site and Instrumentation
3. Methodology
3.1. Halo Lidar Toolbox
- Background correction has been applied to the raw data with methods published by [62,63]. A correction for the telescope focus of the instrument was also applied to the signal, as explained in [60]. The instrumental precision of radial velocities was estimated with the method given by [27,70], and attenuated backscatter coefficient () with uncertainties were also calculated [64];
- From scanning measurements, three-dimensional wind vector profiles were calculated using the least squares method with singular value decomposition by assuming a stationary and horizontally homogeneous wind field, and radial velocity uncertainties were propagated to wind components as described by [65]. The wind component uncertainties were estimated with the method described by [66];
- The vertical velocity statistical momenta, i.e., variance, skewness, and kurtosis, were calculated from vertically pointing measurements at 3, 30, and 60 min resolutions. Statistics unbiased by random noise and sample size were calculated as given by [67] and standard errors were estimated with a bootstrap method described by [68];
- Wind shear vector, which can also be a source of turbulent mixing, is also calculated. This vector is calculated from the changes in and wind components with height [61], as:therefore, its module is:
- The dissipation rate of the turbulent kinetic energy, , was calculated from vertically pointing measurements using the method presented by [41]. This quantity was defined as the rate at which the turbulence energy is absorbed by breaking the eddies down into smaller eddies until they are ultimately converted into heat by viscous forces [71], following the Kolmogorov hypothesis [72]. The method applies Taylor’s frozen turbulence hypothesis that eddies travel with the mean wind while maintaining their characteristics [73]. This quantity is then used as an indicator of turbulent mixing, instead of the combination of vertical skewness and variance [14]. The method used also provides an uncertainty estimate for [41];
- Finally, all the previously calculated quantities were combined following a decision tree to create a bitfield-based classification mask. This method was created by [64] following the profile-based Doppler lidar method introduced by [52] with the aim of objectively assigning a dominant source for turbulent mixing. The analyzed regions of the profiles were selected from calibrated to height ranges with sufficient atmospheric signal and no clouds (a threshold 10 Mm−1 sr−1 was used based on the literature [14,52,74]). The presence of turbulence was obtained from with a threshold > 10−5 m2 s−3 or > 10−4 m2 s−3, depending whether the classified heights were below cloud or connected to the surface [64]. All range gates with surface-connected turbulent behavior during daytime were classified as dominated by convective mixing. During night-time, when ABL is assumed to be neutral or stably stratified [71], wind-shear derived turbulence is searched with a threshold > 0.03 s−1 [75]. Finally, range gates that are classified as turbulent but are unconnected to surface or clouds during daytime, and not related to wind shear during night-time, are labelled as ‘intermittent’ since turbulence is assumed to arise from other intermittent sources [76].
3.2. Data Processing
4. Results
4.1. Horizontal Wind Field Characterization
4.2. ABL Turbulent Sources Characterization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Weibull Parameters by Season

References
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; 32p. [Google Scholar]
- Myhre, G.; Shindell, D.; Bréon, F.-M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and natural radiative forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- IPCC. IPCC Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Myhre, G.; Aas, W.; Cherian, R.; Collins, W.; Faluvegi, G.; Flanner, M.; Forster, P.; Hodnebrog, Ø.; Klimont, Z.; Lund, M.T.; et al. Multi-model simulations of aerosol and ozone radiative forcing due to anthropogenic emission changes during the period 1990–2015. Atmos. Chem. Phys. 2017, 17, 2709–2720. [Google Scholar] [CrossRef] [Green Version]
- Baklanov, A.; Grisogono, B.; Bornstein, R.; Mahrt, L.; Zilitinkevich, S.S.; Taylor, P.; Larsen, S.E.; Rotach, M.W.; Fernando, H.J.S. The nature, theory, and modeling of atmospheric planetary boundary layers. Bull. Am. Meteorol. Soc. 2011, 92, 123–128. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Yang, Y.; Hu, X.M.; Huang, Z.; Wang, G.; Zhang, B.; Zhang, T. Evaluation of retrieval methods of daytime convective boundary layer height based on lidar data. J. Geophys. Res. 2017, 122, 4578–4593. [Google Scholar] [CrossRef]
- Illingworth, A.J.; Cimini, D.; Haefele, A.; Haeffelin, M.; Hervo, M.; Kotthaus, S.; Löhnert, U.; Martinet, P.; Mattis, I.; O’Connor, E.J.; et al. How can existing ground-based profiling instruments improve european weather forecasts? Bull. Am. Meteorol. Soc. 2019, 100, 605–620. [Google Scholar] [CrossRef]
- World-Meteorological-Organization Statement of Guidance for High Resolution Numerical Weather Prediction (NWP). Technical Report. 2018. Available online: www.wmo.int/pages/prog/www/OSY/SOG/SoG-HighRes-NWP.pdf (accessed on 14 December 2020).
- Benavent-Oltra, J.A.; Román, R.; Andrés Casquero-Vera, J.; Pérez-Ramírez, D.; Lyamani, H.; Ortiz-Amezcua, P.; Bedoya-Velásquez, A.E.; De Arruda Moreira, G.; Barreto, Á.; Lopatin, A.; et al. Different strategies to retrieve aerosol properties at night-time with the GRASP algorithm. Atmos. Chem. Phys. 2019, 19, 14149–14171. [Google Scholar] [CrossRef] [Green Version]
- Bedoya-Velásquez, A.E.; Navas-Guzmán, F.; Granados-Muñoz, M.J.; Titos, G.; Román, R.; Andrés Casquero-Vera, J.; Ortiz-Amezcua, P.; Antonio Benavent-Oltra, J.; De Arruda Moreira, G.; Montilla-Rosero, E.; et al. Hygroscopic growth study in the framework of EARLINET during the SLOPE i campaign: Synergy of remote sensing and in situ instrumentation. Atmos. Chem. Phys. 2018, 18, 7001–7017. [Google Scholar] [CrossRef] [Green Version]
- Casquero-Vera, J.A.; Lyamani, H.; Dada, L.; Hakala, S.; Paasonen, P.; Román, R.; Fraile, R.; Petäjä, T.; Olmo-Reyes, F.J.; Alados-Arboledas, L. New particle formation at urban and high-altitude remote sites in the south-eastern Iberian Peninsula. Atmos. Chem. Phys. 2020, 20, 14253–14271. [Google Scholar] [CrossRef]
- Benavent-Oltra, J.A.; Casquero-Vera, J.A.; Román, R.; Lyamani, H.; Pérez-Ramírez, D.; Granados-Muñoz, M.J.; Cazorla, A.; Ortiz-Amezcua, P.; Bedoya-Velásquez, A.E.; de Arruda Moreira, G.; et al. Overview of SLOPE I and II campaigns: Aerosol properties retrieved with lidar and sun-sky photometer measurements. Atmos. Chem. Phys. 2020, 21, 9269–9287. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: London, UK, 1992. [Google Scholar]
- Hogan, R.J.; Grant, A.L.M.; Illingworth, A.J.; Pearson, G.N.; O’Connor, E.J. Vertical velocity variance and skewness in clear and cloud-topped boundary layers as revealed by Doppler lidar. Q. J. R. Meteorol. Soc. 2009, 135, 635–643. [Google Scholar] [CrossRef]
- Wehner, B.; Siebert, H.; Ansmann, A.; Ditas, F.; Seifert, P.; Stratmann, F.; Wiedensohler, A.; Apituley, A.; Shaw, R.A.; Manninen, H.E.; et al. Observations of turbulence-induced new particle formation in the residual layer. Atmos. Chem. Phys. 2010, 10, 4319–4330. [Google Scholar] [CrossRef] [Green Version]
- Pinsky, M.; Khain, A.; Krugliak, H. Collisions of cloud droplets in a turbulent flow. Part V: Application of detailed tables of turbulent collision rate enhancement to simulation of droplet spectra evolution. J. Atmos. Sci. 2008, 65, 357–374. [Google Scholar] [CrossRef]
- Ning, G.; Yim, S.H.L.; Wang, S.; Duan, B.; Nie, C.; Yang, X.; Wang, J.; Shang, K. Synergistic effects of synoptic weather patterns and topography on air quality: A case of the Sichuan Basin of China. Clim. Dyn. 2019, 53, 6729–6744. [Google Scholar] [CrossRef]
- Bossioli, E.; Tombrou, M.; Dandou, A.; Athanasopoulou, E.; Varotsos, K.V. The role of planetary boundary-layer parameterizations in the air quality of an urban area with complex topography. Bound. Layer Meteorol. 2009, 131, 53–72. [Google Scholar] [CrossRef]
- Bedoya-Velásquez, A.E.; Navas-Guzmán, F.; de Arruda Moreira, G.; Román, R.; Cazorla, A.; Ortiz-Amezcua, P.; Benavent-Oltra, J.A.; Alados-Arboledas, L.; Olmo-Reyes, F.J.; Foyo-Moreno, I.; et al. Seasonal analysis of the atmosphere during five years by using microwave radiometry over a mid-latitude site. Atmos. Res. 2019, 218, 78–89. [Google Scholar] [CrossRef] [Green Version]
- de Arruda Moreira, G.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Benavent-Oltra, J.A.; Ortiz-Amezcua, P.; Róman, R.; Bedoya-Velásquez, A.E.; Landulfo, E.; Alados-Arboledas, L. Study of the planetary boundary layer by microwave radiometer, elastic lidar and Doppler lidar estimations in southern Iberian Peninsula. Atmos. Res. 2018, 213, 185–195. [Google Scholar] [CrossRef] [Green Version]
- de Arruda Moreira, G.; Guerrero-Rascado, J.L.; Benavent-Oltra, J.A.; Ortiz-Amezcua, P.; Román, R.; Bedoya-Velásquez, A.E.; Bravo-Aranda, J.A.; Reyes, F.J.O.; Landulfo, E.; Alados-Arboledas, L. Analyzing the turbulent planetary boundary layer by remote sensing systems: The Doppler wind lidar, aerosol elastic lidar and microwave radiometer. Atmos. Chem. Phys. 2019, 19, 1263–1280. [Google Scholar] [CrossRef] [Green Version]
- de Arruda Moreira, G.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Foyo-Moreno, I.; Cazorla, A.; Alados, I.; Lyamani, H.; Landulfo, E.; Alados-Arboledas, L. Study of the planetary boundary layer height in an urban environment using a combination of microwave radiometer and ceilometer. Atmos. Res. 2020, 240, 104932. [Google Scholar] [CrossRef]
- Lyamani, H.; Fernández-Gálvez, J.; Pérez-Ramírez, D.; Valenzuela, A.; Antón, M.; Alados, I.; Titos, G.; Olmo, F.J.; Alados-Arboledas, L. Aerosol properties over two urban sites in South Spain during an extended stagnation episode in winter season. Atmos. Environ. 2012, 62, 424–432. [Google Scholar] [CrossRef]
- Casquero-Vera, J.A.; Lyamani, H.; Titos, G.; Borrás, E.; Olmo, F.J.; Alados-Arboledas, L. Impact of primary NO2 emissions at different urban sites exceeding the European NO2 standard limit. Sci. Total Environ. 2019, 646, 1117–1125. [Google Scholar] [CrossRef]
- Frehlich, R.; Hannon, S.M.; Henderson, S.W. Performance of a 2-μm coherent Doppler lidar for wind measurements. J. Atmos. Ocean. Technol. 1994, 11, 1517–1528. [Google Scholar] [CrossRef]
- Frehlich, R. Estimation of velocity error for Doppler lidar measurements. J. Atmos. Ocean. Technol. 2001, 18, 1628–1639. [Google Scholar] [CrossRef]
- Pearson, G.; Davies, F.; Collier, C. An analysis of the performance of the UFAM pulsed Doppler lidar for observing the boundary layer. J. Atmos. Ocean. Technol. 2009, 26, 240–250. [Google Scholar] [CrossRef]
- Witschas, B.; Lemmerz, C.; Geiß, A.; Lux, O.; Marksteiner, U.; Rahm, S.; Reitebuch, O.; Weiler, F. First validation of Aeolus wind observations by airborne Doppler wind lidar measurements. Atmos. Meas. Tech. 2020, 13, 2381–2396. [Google Scholar] [CrossRef]
- Lux, O.; Lemmerz, C.; Weiler, F.; Marksteiner, U.; Witschas, B.; Rahm, S.; Geiß, A.; Reitebuch, O. Intercomparison of wind observations from the European Space Agency’s Aeolus satellite mission and the ALADIN Airborne Demonstrator. Atmos. Meas. Tech. 2020, 13, 2075–2097. [Google Scholar] [CrossRef] [Green Version]
- Baars, H.; Herzog, A.; Heese, B.; Ohneiser, K.; Hanbuch, K.; Hofer, J.; Yin, Z.; Engelmann, R.; Wandinger, U. Validation of Aeolus wind products above the Atlantic Ocean. Atmos. Meas. Tech. Discuss. 2020, 2020, 1–27. [Google Scholar] [CrossRef]
- Liu, Z.; Barlow, J.F.; Chan, P.W.; Fung, J.C.H.; Li, Y.; Ren, C.; Mak, H.W.L.; Ng, E. A review of progress and applications of pulsed Doppler wind LiDARs. Remote Sens. 2019, 11, 2522. [Google Scholar] [CrossRef] [Green Version]
- Shun, C.M.; Chan, P.W. Applications of an infrared Doppler lidar in detection of wind shear. J. Atmos. Ocean. Technol. 2008, 25, 637–655. [Google Scholar] [CrossRef]
- Nechaj, P.; Gaál, L.; Bartok, J.; Vorobyeva, O.; Gera, M.; Kelemen, M.; Polishchuk, V. Monitoring of low-level wind shear by ground-based 3D lidar for increased flight safety, protection of human lives and health. Int. J. Environ. Res. Public Health 2019, 16, 4584. [Google Scholar] [CrossRef] [Green Version]
- Banta, R.M.; Darby, L.S.; Fast, J.D.; Pinto, J.O.; Whiteman, C.D.; Shaw, W.J.; Orr, B.W. Nocturnal low-level jet in a mountain basin complex. Part I: Evolution and effects on local flows. J. Appl. Meteorol. 2004, 43, 1348–1365. [Google Scholar] [CrossRef]
- Marke, T.; Crewell, S.; Schemann, V.; Schween, J.H.; Tuononen, M. Long-term observations and high-resolution modeling of midlatitude nocturnal boundary layer processes connected to low-level jets. J. Appl. Meteorol. Climatol. 2018, 57, 1155–1170. [Google Scholar] [CrossRef]
- Tuononen, M.; O’Connor, E.J.; Sinclair, V.A.; Vakkari, V. Low-level jets over Utö, Finland, based on Doppler lidar observations. J. Appl. Meteorol. Climatol. 2017, 56, 2577–2594. [Google Scholar] [CrossRef]
- Suomi, I.; Gryning, S.E.; O’Connor, E.J.; Vihma, T. Methodology for obtaining wind gusts using Doppler lidar. Q. J. R. Meteorol. Soc. 2017, 143, 2061–2072. [Google Scholar] [CrossRef] [Green Version]
- Pantillon, F.; Adler, B.; Corsmeier, U.; Knippertz, P.; Wieser, A.; Hansen, A. Formation of wind gusts in an extratropical cyclone in light of Doppler lidar observations and large-eddy simulations. Mon. Weather Rev. 2019, 148, 353–375. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J.; Gottschall, J.; Courtney, M.S. Can wind lidars measure turbulence? J. Atmos. Ocean. Technol. 2011, 28, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Banakh, V.A.; Smalikho, I.N.; Köpp, F.; Werner, C. Measurements of turbulent energy dissipation rate with a CW Doppler lidar in the atmospheric boundary layer. J. Atmos. Ocean. Technol. 1999, 16, 1044–1061. [Google Scholar] [CrossRef]
- O’Connor, E.J.; Illingworth, A.J.; Brooks, I.M.; Westbrook, C.D.; Hogan, R.J.; Davies, F.; Brooks, A.B.J. A method for estimating the turbulent kinetic energy dissipation rate from a vertically pointing Doppler lidar, and independent evaluation from balloon-borne in situ measurements. J. Atmos. Ocean. Technol. 2010, 27, 1652–1664. [Google Scholar] [CrossRef] [Green Version]
- Vakkari, V.; O’Connor, E.J.; Nisantzi, A.; Mamouri, R.E.; Hadjimitsis, D.G. Low-level mixing height detection in coastal locations with a scanning Doppler lidar. Atmos. Meas. Tech. 2015, 8, 1875–1885. [Google Scholar] [CrossRef] [Green Version]
- Tucker, S.C.; Brewer, W.A.; Banta, R.M.; Senff, C.J.; Sandberg, S.P.; Law, D.C.; Weickmann, A.M.; Hardesty, R.M. Doppler lidar estimation of mixing height using turbulence, shear, and aerosol profiles. J. Atmos. Ocean. Technol. 2009, 16, 673–688. [Google Scholar] [CrossRef]
- Schween, J.H.; Hirsikko, A.; Löhnert, U.; Crewell, S. Mixing-layer height retrieval with ceilometer and Doppler lidar: From case studies to long-term assessment. Atmos. Meas. Tech. 2014, 7, 3685–3704. [Google Scholar] [CrossRef] [Green Version]
- Engelmann, R.; Wandinger, U.; Ansmann, A.; Müller, D.; Žeromskis, E.; Althausen, D.; Wehner, B. Lidar observations of the vertical aerosol flux in the planetary boundary layer. J. Atmos. Ocean. Technol. 2008, 25, 1296–1306. [Google Scholar] [CrossRef]
- Lane, S.E.; Barlow, J.F.; Wood, C.R. An assessment of a three-beam Doppler lidar wind profiling method for use in urban areas. J. Wind Eng. Ind. Aerodyn. 2013, 119, 53–59. [Google Scholar] [CrossRef] [Green Version]
- van Dinther, D.; Wood, C.R.; Hartogensis, O.K.; Nordbo, A.; O’Connor, E.J. Observing crosswind over urban terrain using scintillometer and Doppler lidar. Atmos. Meas. Tech. 2015, 8, 1901–1911. [Google Scholar] [CrossRef] [Green Version]
- Drew, D.R.; Barlow, J.F.; Lane, S.E. Observations of wind speed profiles over Greater London, UK, using a Doppler lidar. J. Wind Eng. Ind. Aerodyn. 2013, 121, 98–105. [Google Scholar] [CrossRef] [Green Version]
- Kikumoto, H.; Ooka, R.; Sugawara, H.; Lim, J. Observational study of power-law approximation of wind profiles within an urban boundary layer for various wind conditions. J. Wind Eng. Ind. Aerodyn. 2017, 164, 13–21. [Google Scholar] [CrossRef]
- Wood, C.R.; Pauscher, L.; Ward, H.C.; Kotthaus, S.; Barlow, J.F.; Gouvea, M.; Lane, S.E.; Grimmond, C.S.B. Wind observations above an urban river using a new lidar technique, scintillometry and anemometry. Sci. Total Environ. 2013, 442, 527–533. [Google Scholar] [CrossRef] [Green Version]
- Kent, C.W.; Grimmond, C.S.B.; Gatey, D.; Barlow, J.F. Assessing methods to extrapolate the vertical wind-speed profile from surface observations in a city centre during strong winds. J. Wind Eng. Ind. Aerodyn. 2018, 173, 100–111. [Google Scholar] [CrossRef]
- Harvey, N.J.; Hogan, R.J.; Dacre, H.F. A method to diagnose boundary-layer type using Doppler lidar. Q. J. R. Meteorol. Soc. 2013, 139, 1681–1693. [Google Scholar] [CrossRef]
- Illingworth, A.J.; Hogan, R.J.; O’Connor, E.J.; Bouniol, D.; Brooks, M.E.; Delanoë, J.; Donovan, D.P.; Eastment, J.D.; Gaussiat, N.; Goddard, J.W.F.; et al. Cloudnet: Continuous evaluation of cloud profiles in seven operational models using ground-based observations. Bull. Am. Meteorol. Soc. 2007, 88, 883–898. [Google Scholar] [CrossRef] [Green Version]
- Illingworth, A.J.; Cimini, D.; Gaffard, C.; Haeffelin, M.; Lehmann, V.; Löhnert, U.; O’Connor, E.J.; Ruffieux, D. Exploiting existing ground-based remote sensing networks to improve high-resolution weather forecasts. Bull. Am. Meteorol. Soc. 2015, 96, 2107–2125. [Google Scholar] [CrossRef]
- Cimini, D.; Haeffelin, M.; Kotthaus, S.; Löhnert, U.; Martinet, P.; O’Connor, E.; Walden, C.; Coen, M.C.; Preissler, J. Towards the profiling of the atmospheric boundary layer at European scale—Introducing the COST Action PROBE. Bull. Atmos. Sci. Technol. 2020, 1, 23–42. [Google Scholar] [CrossRef] [Green Version]
- Manninen, A.J. Halo Lidar Toolbox. Available online: https://github.com/manninenaj/HALO_lidar_toolbox (accessed on 1 March 2019).
- Bosque Maurel, J. El clima de Granada. Estud. Geográficos 1959, 20, 145–147. [Google Scholar]
- Viedma Muñoz, M. Análisis de loas direcciones de los vientos en Andalucía. Nimbus 1998, 1, 153–168. [Google Scholar]
- Montávez, J.P.; Rodríguez, A.; Jiménez, J.I. A study of the urban heat island of Granada. Int. J. Climatol. 2000, 20, 899–911. [Google Scholar] [CrossRef]
- Pentikäinen, P.; James O’connor, E.; Manninen, A.J.; Ortiz-Amezcua, P. Methodology for deriving the telescope focus function and its uncertainty for a heterodyne pulsed Doppler lidar. Atmos. Meas. Tech. 2020, 13, 2849–2863. [Google Scholar] [CrossRef]
- ICAO. Manual on Low-level Wind Shear. Doc 9817 AN/449, 1st ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2005; 222p. [Google Scholar]
- Manninen, A.J.; O’Connor, E.J.; Vakkari, V.; Petäjä, T. A generalised background correction algorithm for a Halo Doppler lidar and its application to data from Finland. Atmos. Meas. Tech. 2016, 9, 817–827. [Google Scholar] [CrossRef] [Green Version]
- Vakkari, V.; Manninen, A.J.; O’Connor, E.J.; Schween, J.H.; Van Zyl, P.G.; Marinou, E. A novel post-processing algorithm for Halo Doppler lidars. Atmos. Meas. Tech. 2019, 12, 839–852. [Google Scholar] [CrossRef] [Green Version]
- Manninen, A.J.; Marke, T.; Tuononen, M.; O’Connor, E.J. Atmospheric boundary layer classification with Doppler lidar. J. Geophys. Res. Atmos. 2018, 123, 8172–8189. [Google Scholar] [CrossRef]
- Päschke, E.; Leinweber, R.; Lehmann, V. An assessment of the performance of a 1.5 μm Doppler lidar for operational vertical wind profiling based on a 1-year trial. Atmos. Meas. Tech. 2015, 8, 22151–22266. [Google Scholar] [CrossRef] [Green Version]
- Newsom, R.K.; Alan Brewer, W.; Wilczak, J.M.; Wolfe, D.E.; Oncley, S.P.; Lundquist, J.K. Validating precision estimates in horizontal wind measurements from a Doppler lidar. Atmos. Meas. Tech. 2017, 10, 1229–1240. [Google Scholar] [CrossRef] [Green Version]
- Rimoldini, L. Weighted skewness and kurtosis unbiased by sample size and Gaussian uncertainties. Astron. Comput. 2014, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kleiner, A.; Talwalkar, A.; Sarkar, P.; Jordan, M.I. A scalable bootstrap for massive data. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 795–816. [Google Scholar] [CrossRef] [Green Version]
- Baklanov, A.; Grisigono, B. Atmospheric Boundary Layers: Nature, Theory and Applications to Environmental Modelling and Security; Springer: New York, NY, USA, 2008; ISBN 9780387743189. [Google Scholar]
- Rye, B.J.; Hardesty, R.M. Estimate optimization parameters for incoherent backscatter heterodyne lidar. Appl. Opt. 1997, 36, 9425–9436. [Google Scholar] [CrossRef] [PubMed]
- Garrat, J.R. The Atmospheric Boundary Layer; Houghton, J.T., Rycroft, M.J., Dessler, A.J., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1992. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large reynolds’ numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Taylor, G.I. Statistical theory of turbulence. Proc. R. Soc. A Math. Phys. Eng. Sci. 1935, 151, 421–444. [Google Scholar] [CrossRef] [Green Version]
- Westbrook, C.D.; Illingworth, A.J.; O’Connor, E.J.; Hogan, R.J. Doppler lidar measurements of oriented planar ice crystals falling from supercooled and glaciated layer clouds. Q. J. R. Meteorol. Soc. 2010, 136, 260–276. [Google Scholar] [CrossRef] [Green Version]
- Manninen, A.J. Developing Methods for Doppler Lidar to Investigate Atmospheric Boundary Layer; University of Helsinki: Helsinki, Finland, 2019. [Google Scholar]
- Lothon, M.; Lohou, F.; Pino, D.; Couvreux, F.; Pardyjak, E.R.; Reuder, J.; Vilà-Guerau De Arellano, J.; Durand, P.; Hartogensis, O.; Legain, D.; et al. The BLLAST field experiment: Boundary-layer late afternoon and sunset turbulence. Atmos. Chem. Phys. 2014, 14, 931–960. [Google Scholar] [CrossRef] [Green Version]
- Granados-Muñoz, M.J.; Navas-Guzmán, F.; Bravo-Aranda, J.A.; Guerrero-Rascado, J.L.; Lyamani, H.; Fernández-Gálvez, J.; Alados-Arboledas, L. Automatic determination of the planetary boundary layer height using lidar: One-year analysis over southeastern Spain. J. Geophys. Res. Atmos. 2012, 117, D18208. [Google Scholar] [CrossRef] [Green Version]
- US-EPA (United States Environmental Protection Agency). Meteorological Monitoring Guidance for Regulatory Modeling Applications; Office of Air Quality Planning and Standards: Durham, NC, USA, 2000.
- Atmospheric Research and Technology LLC Vector vs. Scalar Averaging of Wind Data. Available online: http://www.sodar.com/FYI/vector_vs_scalar.html (accessed on 14 December 2020).
- Grange, S.K. Technical Note: Averaging Wind Speeds and Directions; University of Auckland: Auckland, New Zealand, 2014. [Google Scholar]
- Stull, R. Practical Meteorology: An Algebra-Based Survey of Atmospheric Science; University of British Columbia: Vancouver, BC, Canada, 2017; ISBN 978-0-88865-283-6. [Google Scholar]
- Jammalamadaka, S.R.; SenGupta, A. Topics in Circular Statistics; World Scientific: Singapore, 2001; ISBN 9789712779267. [Google Scholar]
- Jones, T.A. MATLAB functions to analyze directional (azimuthal) data-I: Single-sample inference. Comput. Geosci. 2006, 32, 166–175. [Google Scholar] [CrossRef]
- American Meteorological Society Glossary of Meteorology, 2nd ed.; American Meteorological Society: Boston, MA, USA, 2000.
- Blackadar, A.K. Boundary layer wind maxima and their significance for the growth of nocturnal inversions. Bull. Am. Meteorol. Soc. 1957, 38, 283–290. [Google Scholar] [CrossRef] [Green Version]
- Baars, H.; Ansmann, A.; Engelmann, R.; Althausen, D. Continuous monitoring of the boundary-layer top with lidar. Atmos. Chem. Phys. 2008, 8, 7281–7296. [Google Scholar] [CrossRef] [Green Version]







| Emission | |
| Wavelength | 1500 nm |
| Pulse energy | 100 µJ |
| Pulse duration | 200 ns |
| Pulse repetition rate | 15 kHz |
| Reception optics | |
| Telescope | monostatic optic-fiber coupled |
| Physical lens diameter | 75 mm |
| Effective beam diameter * | (17.5 ± 1) mm |
| Lens divergence | 33 µrad |
| Focal length * | (535 ± 35) m |
| Detection | |
| Detection type | Heterodyne |
| Range resolution | 30 m |
| Points per range bin | 10 |
| Sampling frequency | 50 MHz |
| Velocity resolution | 0.0382 m s−1 |
| Nyquist velocity | 20 m s−1 |
| DJF | MAM | JJA | SON | |
|---|---|---|---|---|
| ‘Day’ interval (h UTC) | 10–18 | 10–22 | 10–21 | 9–20 |
| ‘Night’ interval (h UTC) | 20–9 | 23–7 | 1–8 | 22–7 |
| Daytime | Night-Time | |||||
|---|---|---|---|---|---|---|
| Altitude a.g.l. (m) | 580–820 (Figure 5a) | 340–580 (Figure 5c) | 100–340 (Figure 5e) | 580–820 (Figure 5b) | 340–580 (Figure 5d) | 100–340 (Figure 5f) |
| 289.7 | 293.4 | 299.1 | 61.6 | 85.0 | 106.4 | |
| 1.0 | 1.4 | 2.0 | 2.1 | 6.3 | 5.0 | |
| 0.95 | 0.92 | 0.87 | 0.48 | 0.25 | 0.14 | |
| 213.8 | 205.8 | 205.3 | 233.3 | 0.0 | 91.5 | |
| 15.0 | 10.0 | 5.0 | 0.9 | 0.03 | 0.5 | |
| 0.05 | 0.08 | 0.13 | 0.52 | 0.75 | 0.86 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortiz-Amezcua, P.; Martínez-Herrera, A.; Manninen, A.J.; Pentikäinen, P.P.; O’Connor, E.J.; Guerrero-Rascado, J.L.; Alados-Arboledas, L. Wind and Turbulence Statistics in the Urban Boundary Layer over a Mountain–Valley System in Granada, Spain. Remote Sens. 2022, 14, 2321. https://doi.org/10.3390/rs14102321
Ortiz-Amezcua P, Martínez-Herrera A, Manninen AJ, Pentikäinen PP, O’Connor EJ, Guerrero-Rascado JL, Alados-Arboledas L. Wind and Turbulence Statistics in the Urban Boundary Layer over a Mountain–Valley System in Granada, Spain. Remote Sensing. 2022; 14(10):2321. https://doi.org/10.3390/rs14102321
Chicago/Turabian StyleOrtiz-Amezcua, Pablo, Alodía Martínez-Herrera, Antti J. Manninen, Pyry P. Pentikäinen, Ewan J. O’Connor, Juan Luis Guerrero-Rascado, and Lucas Alados-Arboledas. 2022. "Wind and Turbulence Statistics in the Urban Boundary Layer over a Mountain–Valley System in Granada, Spain" Remote Sensing 14, no. 10: 2321. https://doi.org/10.3390/rs14102321
APA StyleOrtiz-Amezcua, P., Martínez-Herrera, A., Manninen, A. J., Pentikäinen, P. P., O’Connor, E. J., Guerrero-Rascado, J. L., & Alados-Arboledas, L. (2022). Wind and Turbulence Statistics in the Urban Boundary Layer over a Mountain–Valley System in Granada, Spain. Remote Sensing, 14(10), 2321. https://doi.org/10.3390/rs14102321