Global Evapotranspiration Datasets Assessment Using Water Balance in South America
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Global Evapotranspiration Datasets
2.2.1. Remote-Sensing-Based Datasets
| Model | Methods | Spatial Resolution | Temporal Resolution | Remote Sensing Source | Remote Sensing Drivers | Meteorological Drivers | References |
|---|---|---|---|---|---|---|---|
| BESS | Biophysical process-based model | 5 km | 8 days | MODIS | Atmospheric data (aerosol, water vapor, cloud, atmospheric profile) Surface properties (surface temperature, land cover, leaf area index, albedo) | Global meteorology (MODIS, ERA Interim and NCEP/NCAR) | Jiang and Ryu [75]; Ryu et al. [18] |
| ERA5 (v. Land) | Land-surface model (CHTESSEL) | 0.1 degree | Hourly | MODIS, SPOT-Vegetation | Vegetation phenology (leaf area index, vegetation index) Surface properties (land cover) | Global meteorology (ERA5) | Hersbach et al. [35]; Nogueira et al. [76] |
| GLDAS (v. 2.1) | Land-surface model (NOAH) | 0.25 degree | 3-hourly | MODIS GPCP | Surface properties Precipitation | Global meteorology (AGRMET) and global data assimilation (GDAS) | Rodel et al. [34] |
| GLEAM (v. 3.3b) | Remote sensing (Priestley–Taylor equation) | 0.25 degree | Daily | AIRS, CERES, MODIS, ESA-CCI, SMOS | Atmospheric data (radiation, precipitation, air temperature, lightning frequency) Surface properties (snow water equivalent, multisource soil moisture, vegetation cover fraction, vegetation optical depth) | -- | Martens et al. [71]; Miralles et al. [26] |
| MOD16 (v. 6) | Remote sensing (Penman–Monteith equation) | 500 m | 8 days | MODIS | Vegetation phenology (leaf area index) Surface properties (land cover, albedo, emissivity) | Global meteorology (MERRA-2) | Mu et al. [25,77] |
| PML (v. 2) | Remote sensing (Penman–Monteith equation) | 500 m | 8 days | MODIS | Vegetation phenology (leaf area index, fraction of photosynthetically active radiation) Surface properties (land cover, albedo) | Global meteorology (GLDAS) | Zhang et al. [73] |
| SSEBOP (v. 4) | Remote Sensing (Simplified surface energy balance) | 1 km | Monthly | MODIS | Thermal data (land surface temperature) Multispectral data (surface reflectance) | Global meteorology (GLDAS) | Senay et al. [24,78] |
| Terra Climate | One-dimensional water balance (modified Thornthwaite–Mather equation) | 2.5 arcmin | Monthly | -- | -- | Global meteorology (WorldClim and JRA55) | Abatzoglou et al. [29] |
2.2.2. Comprehensive-Model-Based Approaches
2.3. Water-Balance Estimation of Evapotranspiration
2.4. Seasonal and Interannual Assessments of Evapotranspiration
2.5. Assessment of the Accuracy of Global Evapotranspiration
3. Results and Discussion
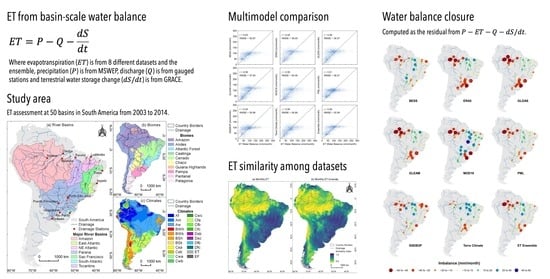
3.1. Evapotranspiration Comparison between Water Balance and Global Datasets
3.2. Seasonal and Interannual Assessment of Evapotranspiration
3.3. Water-Balance Closure
4. Conclusions
- i.
- How consistent are estimates from global datasets based on remote-sensing, reanalysis, land-surface, and biophysical models when compared to ?Our results indicate similar errors when are compared with the water-balance approach (), with moderate correlations and a slight tendency of overestimation in most of South American climates. However, basins located in tropical (and subtropical) humid climates presented lower accuracy and weaker correlations when compared to basins located in tropical seasonal (wet-to-dry) and semiarid climates, suggesting that global datasets have closer agreement with in basins with stronger seasonality, when is mainly driven by water availability.
- ii.
- Do they coherently represent its magnitude and seasonality?Most presented a similar seasonal pattern in the assessed basins, with estimates generally falling within the deviation range, with basins located in tropical seasonal (wet-to-dry) climates achieving a closer agreement. Nevertheless, in humid climates (especially in the tropics) we found higher differences, with yielding different timing and magnitude when compared to , with an overall tendency of overestimation.
- iii.
- How do they agree in terms of seasonal and interannual variability?Our results indicate a strong disagreement in the seasonal and interannual variability between and in the humid tropics. However, in tropical seasonal (wet-to-dry) and subtropical climates, we found higher agreement between for detection of wet and dry anomalous events. These findings also agree with the similarity assessment, with lower similarity in the humid tropics (Amazon biome) and higher similarity in the Cerrado, Caatinga, Pantanal, Atlantic Forest and Pampa biomes. Overall, similarities were higher for monthly than monthly anomalies in these biomes.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to 2019. Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Wright, J.S.; Fu, R.; Worden, J.R.; Chakraborty, S.; Clinton, N.E.; Risi, C.; Sun, Y.; Yin, L. Rainforest-initiated wet season onset over the southern Amazon. Proc. Natl. Acad. Sci. USA 2017, 114, 8481–8486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fisher, J.B.; Malhi, Y.; Bonal, D.; Da Rocha, H.R.; De Araújo, A.C.; Gamo, M.; Goulden, M.L.; Rano, T.H.; Huete, A.R.; Kondo, H.; et al. The land-atmosphere water flux in the tropics. Glob. Chang. Biol. 2009, 15, 2694–2714. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.-F.; Barbosa, H.M.J.; van der Ent, R.J.; Donges, J.F.; Heinke, J.; Sampaio, G.; Rammig, A. On the importance of cascading moisture recycling in South America. Atmos. Chem. Phys. 2014, 14, 13337–13359. [Google Scholar] [CrossRef] [Green Version]
- Martinelli, L.A.; Naylor, R.; Vitousek, P.M.; Moutinho, P. Agriculture in Brazil: Impacts, costs, and opportunities for a sustainable future. Curr. Opin. Environ. Sustain. 2010, 2, 431–438. [Google Scholar] [CrossRef]
- Spera, S.A.; Galford, G.L.; Coe, M.T.; Macedo, M.N.; Mustard, J.F. Land-use change affects water recycling in Brazil’s last agricultural frontier. Glob. Chang. Biol. 2016, 22, 3405–3413. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. The ESA Climate Change Initiative: Satellite Data Records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef] [Green Version]
- Sachs, J.D. From millennium development goals to sustainable development goals. Lancet 2012, 379, 2206–2211. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.G.M.; Molden, D.; Cheema, M.J.M. Basin-wide water accounting based on remote sensing data: An application for the Indus Basin. Hydrol. Earth Syst. Sci. 2013, 17, 2473–2486. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, K. Measuring Sustainability in the UN System of Environmental-Economic Accounting. Environ. Resour. Econ. 2016, 64, 25–36. [Google Scholar] [CrossRef]
- Cuxart, J.; Boone, A.A. Evapotranspiration over Land from a Boundary-Layer Meteorology Perspective. Bound.-Layer Meteorol. 2020, 177, 427–459. [Google Scholar] [CrossRef]
- Shrestha, P.; Simmer, C. Modeled Land Atmosphere Coupling Response to Soil Moisture Changes with Different Generations of Land Surface Models. Water 2020, 12, 46. [Google Scholar] [CrossRef] [Green Version]
- Pielke, R.A.; Avissar, R.; Raupach, M.; Dolman, A.J.; Zeng, X.B.; Denning, A.S. Interactions between the atmosphere and terrestrial ecosystems: Influence on weather and climate. Glob. Chang. Biol. 1998, 4, 461–475. [Google Scholar] [CrossRef]
- Rajib, A.; Evenson, G.R.; Golden, H.E.; Lane, C.R. Hydrologic model predictability improves with spatially explicit calibration using remotely sensed evapotranspiration and biophysical parameters. J. Hydrol. 2018, 567, 668–683. [Google Scholar] [CrossRef] [PubMed]
- Nijzink, R.C.; Almeida, S.; Pechlivanidis, I.G.; Capell, R.; Gustafssons, D.; Arheimer, B.; Parajka, J.; Freer, J.; Han, D.; Wagener, T.; et al. Constraining Conceptual Hydrological Models With Multiple Information Sources. Water Resour. Res. 2018, 54, 8332–8362. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef] [Green Version]
- Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; van Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; van Gorsel, E.; Knohl, A.; Law, B.E.; et al. Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Glob. Biogeochem. Cycles 2011, 25, GB4017. [Google Scholar] [CrossRef] [Green Version]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Kar, S.K. Evapotranspiration Estimation with Remote Sensing and Various Surface Energy Balance Algorithms—A Review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef] [Green Version]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2011, 116, G00J07. [Google Scholar] [CrossRef] [Green Version]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef] [Green Version]
- Pascolini-Campbell, M.A.; Reager, J.T.; Fisher, J.B. GRACE-based Mass Conservation as a Validation Target for Basin-Scale Evapotranspiration in the Contiguous United States. Water Resour. Res. 2020, 56, e2019WR026594. [Google Scholar] [CrossRef]
- Pascolini-Campbell, M.; Reager, J.T.; Chandanpurkar, H.A.; Rodell, M. A 10 per cent increase in global land evapotranspiration from 2003 to 2019. Nature 2021, 593, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, G.; Leuning, R.; Clark, M.; Pitman, A. Evaluating the Performance of Land Surface Models. J. Clim. 2008, 21, 5468–5481. [Google Scholar] [CrossRef]
- Fisher, R.A.; Koven, C.D. Perspectives on the Future of Land Surface Models and the Challenges of Representing Complex Terrestrial Systems. J. Adv. Model. Earth Syst. 2020, 12, e2018MS001453. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Ferguson, C.R.; Sheffield, J.; Wood, E.F.; Gao, H. Quantifying uncertainty in a remote sensing-based estimate of evapotranspiration over continental USA. Int. J. Remote Sens. 2010, 31, 3821–3865. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.B.; Guo, Z.; et al. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38, L06402. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project—Part~2: Evaluation of \hack{\break} global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Wang, L.; Zhou, J.; Li, Y.; Sun, F.; Fu, G.; Li, X.; Sang, Y.-F. A worldwide evaluation of basin-scale evapotranspiration estimates against the water balance method. J. Hydrol. 2016, 538, 82–95. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Pan, N.; Tian, H.; Friedlingstein, P.; Sitch, S.; Shi, H.; Arora, V.K.; Haverd, V.; Jain, A.K.; Kato, E.; et al. Evaluation of global terrestrial evapotranspiration using state-of-the-art approaches in remote sensing, machine learning and land surface modeling. Hydrol. Earth Syst. Sci. 2020, 24, 1485–1509. [Google Scholar] [CrossRef] [Green Version]
- da Motta Paca, V.H.; Espinoza-Dávalos, G.E.; Hessels, T.M.; Moreira, D.M.; Comair, G.F.; Bastiaanssen, W.G.M. The spatial variability of actual evapotranspiration across the Amazon River Basin based on remote sensing products validated with flux towers. Ecol. Process. 2019, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Lakshmi, V.; Wang, D.; Lin, P.; Pan, M.; Cai, X.; Wood, E.F.; Zeng, Z. The Reliability of Global Remote Sensing Evapotranspiration Products over Amazon. Remote Sens. 2020, 12, 2211. [Google Scholar] [CrossRef]
- Baker, J.C.A.; Garcia-Carreras, L.; Gloor, M.; Marsham, J.H.; Buermann, W.; da Rocha, H.R.; Nobre, A.D.; de Araujo, A.C.; Spracklen, D.V. Evapotranspiration in the Amazon: Spatial patterns, seasonality, and recent trends in observations, reanalysis, and climate models. Hydrol. Earth Syst. Sci. 2021, 25, 2279–2300. [Google Scholar] [CrossRef]
- Sörensson, A.A.; Ruscica, R.C. Intercomparison and Uncertainty Assessment of Nine Evapotranspiration Estimates Over South America. Water Resour. Res. 2018, 54, 2891–2908. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; McWilliams, E.B.; Famiglietti, J.S.; Beaudoing, H.K.; Nigro, J. Estimating evapotranspiration using an observation based terrestrial water budget. Hydrol. Process. 2011, 25, 4082–4092. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, K. Comparison of evapotranspiration estimates based on the surface water balance, modified Penman–Monteith model, and reanalysis data sets for continental China. J. Geophys. Res. Atmos. 2017, 122, 3228–3244. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Wang, J.; Feng, J.; Zhang, M. A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sens. 2021, 13, 2414. [Google Scholar] [CrossRef]
- Ramillien, G.; Lombard, A.; Cazenave, A.; Ivins, E.R.; Llubes, M.; Remy, F.; Biancale, R. Interannual variations of the mass balance of the Antarctica and Greenland ice sheets from GRACE. Glob. Planet. Chang. 2006, 53, 198–208. [Google Scholar] [CrossRef]
- Carter, E.; Hain, C.; Anderson, M.; Steinschneider, S. A water balance based, spatiotemporal evaluation of terrestrial evapotranspiration products across the contiguous United States. J. Hydrometeorol. 2018, 19, 891–905. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Abolafia-Rosenzweig, R.; Pan, M.; Zeng, J.L.; Livneh, B. Remotely sensed ensembles of the terrestrial water budget over major global river basins: An assessment of three closure techniques. Remote Sens. Environ. 2021, 252, 112191. [Google Scholar] [CrossRef]
- Moreira, A.A.; Ruhoff, A.L.; Roberti, D.R.; de Arruda Souza, V.; da Rocha, H.R.; de Paiva, R.C.D. Assessment of terrestrial water balance using remote sensing data in South America. J. Hydrol. 2019, 575, 131–147. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [Green Version]
- Turchetto-Zolet, A.C.; Pinheiro, F.; Salgueiro, F.; Palma-Silva, C. Phylogeographical patterns shed light on evolutionary process in South America. Mol. Ecol. 2013, 22, 1193–1213. [Google Scholar] [CrossRef]
- Olson, D.M.; Dinerstein, E.; Wikramanayake, E.D.; Burgess, N.D.; Powell, G.V.N.; Underwood, E.C.; D’amico, J.A.; Itoua, I.; Strand, H.E.; Morrison, J.C.; et al. Terrestrial Ecoregions of the World: A New Map of Life on Earth: A new global map of terrestrial ecoregions provides an innovative tool for conserving biodiversity. Bioscience 2001, 51, 933–938. [Google Scholar] [CrossRef]
- Lucas, E.W.M.; de Sousa, F.D.A.S.; dos Santos Silva, F.D.; da Rocha Júnior, R.L.; Pinto, D.D.C.; da Silva, V.D.P.R. Trends in climate extreme indices assessed in the Xingu river basin—Brazilian Amazon. Weather Clim. Extrem. 2021, 31, 100306. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Sörensson, A.A.; Ronchail, J.; Molina-Carpio, J.; Segura, H.; Gutierrez-Cori, O.; Ruscica, R.; Condom, T.; Wongchuig-Correa, S. Regional hydro-climatic changes in the Southern Amazon Basin (Upper Madeira Basin) during the 1982–2017 period. J. Hydrol. Reg. Stud. 2019, 26, 100637. [Google Scholar] [CrossRef]
- Marengo, J.A.; Souza, C.M.; Thonicke, K.; Burton, C.; Halladay, K.; Betts, R.A.; Alves, L.M.; Soares, W.R. Changes in Climate and Land Use Over the Amazon Region: Current and Future Variability and Trends. Front. Earth Sci. 2018, 6, 228. [Google Scholar] [CrossRef]
- Hilker, T.; Lyapustin, A.I.; Tucker, C.J.; Hall, F.G.; Myneni, R.B.; Wang, Y.; Bi, J.; Mendes de Moura, Y.; Sellers, P.J. Vegetation dynamics and rainfall sensitivity of the Amazon. Proc. Natl. Acad. Sci. USA 2014, 111, 16041–16046. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Bucher, E.H.; Huszar, P.C. Critical environmental costs of the Paraguay-Paraná waterway project in South America. Ecol. Econ. 1995, 15, 3–9. [Google Scholar] [CrossRef]
- Muñoz Garachana, D.; Aragón, R.; Baldi, G. Estructura espacial de remanentes de bosque nativo en el Chaco Seco y el Espinal. Ecol. Austral 2018, 28, 553–564. [Google Scholar] [CrossRef]
- Rodas, O.; Mereles, M.F. El proceso de fragmentación y reducción de hábitat en elChaco Paraguayo y sus efectos sobre la biodiversidad. In El Chaco sin Bosques: La Pampa o el Desirto del Futuro; Morello, J., Roderiguez, A., Eds.; GEPAMA: Buenos Aires, Argentina, 2009; ISBN 9789879260746. [Google Scholar]
- Mataveli, G.A.V.; Pereira, G.; de Oliveira, G.; Seixas, H.T.; Cardozo, F.d.S.; Shimabukuro, Y.E.; Kawakubo, F.S.; Brunsell, N.A. 2020 Pantanal’s widespread fire: Short- and long-term implications for biodiversity and conservation. Biodivers. Conserv. 2021, 30, 3299–3303. [Google Scholar] [CrossRef]
- Wilson, O.J.; Mayle, F.E.; Walters, R.J.; Lingner, D.V.; Vibrans, A.C. Floristic change in Brazil’s southern Atlantic Forest biodiversity hotspot: From the Last Glacial Maximum to the late 21st Century. Quat. Sci. Rev. 2021, 264, 107005. [Google Scholar] [CrossRef]
- Souza, C.M.; Shimbo, J.Z.; Rosa, M.R.; Parente, L.L.; Alencar, A.A.; Rudorff, B.F.T.; Hasenack, H.; Matsumoto, M.; Ferreira, L.G.; Souza-Filho, P.W.M.; et al. Reconstructing Three Decades of Land Use and Land Cover Changes in Brazilian Biomes with Landsat Archive and Earth Engine. Remote Sens. 2020, 12, 2735. [Google Scholar] [CrossRef]
- Nabinger, C.; Dall’ Agnol, M.; Carvalho, P.D. Biodiversidade e produtividade em pastagens. In Proceedings of the XXIII Simpósio Sobre Manejo da Pastagem, Piracicaba, Brazil, 5–7 September 2006; pp. 87–138. [Google Scholar]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Zhao, M.; Running, S. Algorithm Theoretical Basis Document: MODIS Global Terrestrial Evapotranspiration (ET) Product (NASA MOD16A2/A3) Collection 5. NASA Headquarters; National Aeronautics and Space Administration: Washington, DC, USA, 2013. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD16ATBD.pdf (accessed on 20 May 2022).
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Senay, G.B.; Schauer, M.; Friedrichs, M.; Velpuri, N.M.; Singh, R.K. Satellite-based water use dynamics using historical Landsat data (1984–2014) in the southwestern United States. Remote Sens. Environ. 2017, 202, 98–112. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Nogueira, M.; Albergel, C.; Boussetta, S.; Johannsen, F.; Trigo, I.F.; Ermida, S.L.; Martins, J.P.A.; Dutra, E. Role of vegetation in representing land surface temperature in the CHTESSEL (CY45R1) and SURFEX-ISBA (v8.1) land surface models: A case study over Iberia. Geosci. Model Dev. 2020, 13, 3975–3993. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Senay, G.B.; Kagone, S.; Velpuri, N.M. Operational Global Actual Evapotranspiration: Development, Evaluation, and Dissemination. Sensors 2020, 20, 1915. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data Discuss. 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. MSWEP V2 Global 3-Hourly 0.1° Precipitation: Methodology and Quantitative Assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Wilks, D.S. “The Stippling Shows Statistically Significant Grid Points”: How Research Results are Routinely Overstated and Overinterpreted, and What to Do about It. Bull. Am. Meteorol. Soc. 2016, 97, 2263–2273. [Google Scholar] [CrossRef]
- Yamada, T.J.; Koster, R.D.; Kanae, S.; Oki, T. Estimation of Predictability with a Newly Derived Index to Quantify Similarity among Ensemble Members. Mon. Weather Rev. 2007, 135, 2674–2687. [Google Scholar] [CrossRef] [Green Version]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Walker, J.P. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Hasler, N.; Avissar, R. What Controls Evapotranspiration in the Amazon Basin? J. Hydrometeorol. 2007, 8, 380–395. [Google Scholar] [CrossRef]
- Maeda, E.E.; Ma, X.; Wagner, F.H.; Kim, H.; Oki, T.; Eamus, D.; Huete, A. Evapotranspiration seasonality across the Amazon Basin. Earth Syst. Dyn. 2017, 8, 439–454. [Google Scholar] [CrossRef] [Green Version]
- Rubert, G.; Roberti, D.; Pereira, L.; Quadros, F.; Campos Velho, H.; Leal de Moraes, O. Evapotranspiration of the Brazilian Pampa Biome: Seasonality and Influential Factors. Water 2018, 10, 1864. [Google Scholar] [CrossRef] [Green Version]
- De Oliveira, M.L.; dos Santos, C.A.C.; de Oliveira, G.; Perez-Marin, A.M.; Santos, C.A.G. Effects of human-induced land degradation on water and carbon fluxes in two different Brazilian dryland soil covers. Sci. Total Environ. 2021, 792, 148458. [Google Scholar] [CrossRef] [PubMed]
- Cabral, O.M.R.; da Rocha, H.R.; Gash, J.H.; Freitas, H.C.; Ligo, M.A.V. Water and energy fluxes from a woodland savanna (cerrado) in southeast Brazil. J. Hydrol. Reg. Stud. 2015, 4, 22–40. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Zolin, C.A.; Hain, C.R.; Semmens, K.; Tugrul Yilmaz, M.; Gao, F. Comparison of satellite-derived LAI and precipitation anomalies over Brazil with a thermal infrared-based Evaporative Stress Index for 2003–2013. J. Hydrol. 2015, 526, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Marengo, J.A.; Tomasella, J.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A. The drought of 2010 in the context of historical droughts in the Amazon region. Geophys. Res. Lett. 2011, 38, L12703. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46, W12526. [Google Scholar] [CrossRef] [Green Version]
- Filizola, N.; Latrubesse, E.M.; Fraizy, P.; Souza, R.; Guimarães, V.; Guyot, J.-L. Was the 2009 flood the most hazardous or the largest ever recorded in the Amazon? Geomorphology 2014, 215, 99–105. [Google Scholar] [CrossRef]
- Marengo, J.A.; Tomasella, J.; Soares, W.R.; Alves, L.M.; Nobre, C.A. Extreme climatic events in the Amazon basin. Theor. Appl. Climatol. 2012, 107, 73–85. [Google Scholar] [CrossRef]
- Abelen, S.; Seitz, F.; Abarca-del-Rio, R.; Güntner, A. Droughts and Floods in the La Plata Basin in Soil Moisture Data and GRACE. Remote Sens. 2015, 7, 7324–7349. [Google Scholar] [CrossRef] [Green Version]
- Penatti, N.C.; de Almeida, T.I.R.; Ferreira, L.G.; Arantes, A.E.; Coe, M.T. Satellite-based hydrological dynamics of the world’s largest continuous wetland. Remote Sens. Environ. 2015, 170, 1–13. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Wood, E.F. Impact of model structure and parameterization on Penman–Monteith type evaporation models. J. Hydrol. 2015, 525, 521–535. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Biogeosci. 2006, 111, G01002. [Google Scholar] [CrossRef] [Green Version]
- Ruhoff, A.L.; Paz, A.R.; Aragao, L.E.O.C.; Mu, Q.; Malhi, Y.; Collischonn, W.; Rocha, H.R.; Running, S.W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Hydrol. Sci. J. 2013, 58, 1658–1676. [Google Scholar] [CrossRef]
- Pellet, V.; Aires, F.; Yamazaki, D.; Papa, F. Coherent Satellite Monitoring of the Water Cycle Over the Amazon. Part 1: Methodology and Initial Evaluation. Water Resour. Res. 2021, 57, e2020WR028647. [Google Scholar] [CrossRef]
- Fassoni-Andrade, A.; Fleischmann, A.; Papa, F.; Cauduro Dias de Paiva, R.; Wongchuig, S.; Melack, J.; Moreira, A.; Paris, A.; Ruhoff, A.; Barbosa, C.; et al. Amazon hydrology from space: Scientific advances and future challenges. Rev. Geophys. 2021, 59, e2020RG000728. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruhoff, A.; de Andrade, B.C.; Laipelt, L.; Fleischmann, A.S.; Siqueira, V.A.; Moreira, A.A.; Barbedo, R.; Cyganski, G.L.; Fernandez, G.M.R.; Brêda, J.P.L.F.; et al. Global Evapotranspiration Datasets Assessment Using Water Balance in South America. Remote Sens. 2022, 14, 2526. https://doi.org/10.3390/rs14112526
Ruhoff A, de Andrade BC, Laipelt L, Fleischmann AS, Siqueira VA, Moreira AA, Barbedo R, Cyganski GL, Fernandez GMR, Brêda JPLF, et al. Global Evapotranspiration Datasets Assessment Using Water Balance in South America. Remote Sensing. 2022; 14(11):2526. https://doi.org/10.3390/rs14112526
Chicago/Turabian StyleRuhoff, Anderson, Bruno Comini de Andrade, Leonardo Laipelt, Ayan Santos Fleischmann, Vinícius Alencar Siqueira, Adriana Aparecida Moreira, Rafael Barbedo, Gabriele Leão Cyganski, Gabriel Matte Rios Fernandez, João Paulo Lyra Fialho Brêda, and et al. 2022. "Global Evapotranspiration Datasets Assessment Using Water Balance in South America" Remote Sensing 14, no. 11: 2526. https://doi.org/10.3390/rs14112526
APA StyleRuhoff, A., de Andrade, B. C., Laipelt, L., Fleischmann, A. S., Siqueira, V. A., Moreira, A. A., Barbedo, R., Cyganski, G. L., Fernandez, G. M. R., Brêda, J. P. L. F., Paiva, R. C. D. d., Meller, A., Teixeira, A. d. A., Araújo, A. A., Fuckner, M. A., & Biggs, T. (2022). Global Evapotranspiration Datasets Assessment Using Water Balance in South America. Remote Sensing, 14(11), 2526. https://doi.org/10.3390/rs14112526