Coupled Heterogeneous Tucker Decomposition: A Feature Extraction Method for Multisource Fusion and Domain Adaptation Using Multisource Heterogeneous Remote Sensing Data

Abstract

To excavate adequately the rich information contained in multisource remote sensing data, feature extraction as basic yet important research has two typical applications: one of which is to extract complementary information of multisource data to improve classification; and the other is to extract shared information across sources for domain adaptation. However, typical feature extraction methods require the input represented as vectors or homogeneous tensors and fail to process multisource data represented as heterogeneous tensors. Therefore, the coupled heterogeneous Tucker decomposition (C-HTD) containing two sub-methods, namely coupled factor matrix-based HTD (CFM-HTD) and coupled core tensor-based HTD (CCT-HTD), is proposed to establish a unified feature extraction framework for multisource fusion and domain adaptation. To handle multisource heterogeneous tensors, multiple Tucker models were constructed to extract features of different sources separately. To cope with the supervised and semi-supervised cases, the class-indicator factor matrix was built to enhance the separability of features using known labels and learned labels. To mine the complementarity of paired multisource samples, coupling constraint was imposed on multiple factor matrices to form CFM-HTD to extract multisource information jointly. To extract domain-adapted features, coupling constraint was imposed on multiple core tensors to form CCT-HTD to encourage data from different sources to have the same class centroid. In addition, to reduce the impact of interference samples on domain adaptation, an adaptive sample-weighting matrix was designed to autonomously remove outliers. Using multiresolution multiangle optical and MSTAR datasets, experimental results show that the C-HTD outperforms typical multisource fusion and domain adaptation methods.

1. Introduction

The rapid development of satellite sensor technology has provided multisource heterogeneous remote sensing data describing objects with higher resolution, different imaging angles, and different physical properties. Compared with single-source data, the heterogeneous data structure and complex distribution of multisource data make object recognition tasks challenging, which simulates the emergence of various multisource data-based object recognition methods in recent years [1,2,3,4,5].

To ensure effective object recognition results, an effective feature representation is essential to acquire discriminative information from multisource heterogeneous remote sensing data. For the multisource data-based object recognition task, there are two types of requirements for the extracted features, where the former, known as multisource fusion-oriented feature extraction, attempts to excavate the “complementarity” of paired multisource data, and the latter, known as domain adaptation-oriented feature extraction, aims at reducing the “difference” between data obtained from different sources.

1.1. Existing Multisource Fusion-Oriented and Domain Adaptation-Oriented Feature Extraction Methods

As for the multisource fusion-oriented feature extraction methods, the conventional manner is to concatenate paired multisource data into a vector and apply the dimension reduction methods, e.g., principal component analysis (PCA) [6] and linear discriminant analysis (LDA) [7], to obtain the fused features to improve object recognition results. In addition, to better deal with multisource data, the multisource discriminant subspace learning method [8] was constructed to extract an effective representation of multisource features combining least square regression loss and L21 norm regularization term. The multiview K-means (KM) cluster method [9] exploited adaptive weights to fuse the multisource features and meanwhile output the cluster results.

For the domain adaptation-oriented feature extraction methods, they always try to transfer data from different sources into a common space to reduce the feature distribution discrepancy between different sources so that the classifier trained by samples from a particular source can be used to recognize objects described by other sources. For example, the transfer component analysis (TCA) [10] method tried to learn shared features across domains in a reproducing kernel Hilbert space (RKHS) using maximum mean discrepancy (MMD) [11]. The joint distribution adaptation (JDA) [12] extended MMD to measure both marginal and conditional distribution and integrated it with PCA to generate features across domains. Compared with the MMD that was calculated by all the samples from different domains, the active transfer learning (ATL) method [13] tried to select the representative samples used for domain adaptation. The homologous component analysis (HCA) [14] found two totally different but homologous transformations to align the distributions with side information and preserve the conditional distributions.

The above multisource fusion-oriented and domain adaptation-oriented feature extraction methods can only deal with input represented as a vector, while multisource remote sensing data can be naturally represented as a tensor. Among various tensor-oriented feature extraction methods, Tucker decomposition (TD) [15] and CANDECOMP/PARAFAC (CP) decomposition [16] are the most prominent methods, where the former decomposes input of the tensor into the core tensor multiplied by a series of factor matrices along with each mode and the latter decomposes input of the tensor into a sum of rank-1 tensors. Therefore, the CP decomposition can be considered a special case of Tucker decomposition. When performing multisource fusion, data from different sources are cascaded into a large-size tensor, and then a Tucker decomposition method is applied to obtain a compressed representation of these data. Based on Tucker decomposition, multilinear PCA [17] was extended from PCA to extract effective features from the input represented as a high-order tensor directly. In addition, GTDA [18], TLPP [19], and TDLA [20] methods were constructed sequentially to cope with the input represented as a tensor. To obtain the useful feature representations as well as the cluster results, the heterogeneous tensor decomposition (HTD) method was established for feature extraction and cluster task of tensor samples [21]. When facing domain adaptation cases, the conventional Tucker decomposition cannot work well. Nevertheless, there are also some tensor-based feature extraction methods developed to reduce the distribution discrepancy across domains. For example, by extending the correlation alignment method (CORAL) [22] to 3D boosted CORAL [23], the gradient feature-oriented 3D domain adaptation method was built to achieve hyperspectral image classification across domains. In addition, the tensorized principle component align method was extended from the space align method for extracting features across different sources of remote sensing data [24].

1.2. Motivation and Contributions

Since remote sensing data acquired from different types of sensors may present different spatial resolutions or spectral resolutions, they can be naturally represented as tensors with different dimensions, denoted as heterogeneous tensors in this study. The classical multisource fusion-oriented (e.g., TD and HTD) or domain adaptation-oriented feature extraction methods can only accept homogeneous tensors (i.e., tensors with the same dimension) as input and cannot process heterogeneous tensors directly. Although some methods (e.g., [23,24]) can convert data represented as heterogeneous tensors to a vector or homogeneous tensor using permuting tensor or interpolation techniques first to comply with their input requirements and then perform feature extraction. This manner leads to the loss of structure information of remote sensing data and thus affects the subsequent object recognition results [25,26]. For input represented as heterogeneous tensors, it is necessary to analyze this data associatively rather than treating them by stages. In addition, the above multisource fusion-oriented or domain adaptation-oriented feature extraction methods are designed separately, lacking a unified framework to handle feature extraction tasks in different situations jointly.

Motived from the abovementioned, the conventional features tensor extraction method, i.e., Tucker decomposition, is extended to coupled heterogeneous Tucker decomposition (C-HTD) to serve as a unified feature extraction framework to deal with multisource fusion and domain adaptation tasks for multisource heterogeneous data. In detail, the proposed C-HTD consists of two sub-methods, i.e., coupled factor matrix-based heterogeneous Tucker decomposition (CFM-HTD) and coupled core tensor-based heterogeneous Tucker decomposition (CCT-HTD), acting on multisource fusion-oriented and domain adaptation-oriented features extraction, respectively. For CFM-HTD, to excavate the complementary information embedding in multisource heterogeneous data, N paired multisource samples are described as heterogeneous tensors, and then multiple Tucker models are constructed, where each Tucker model is used to decompose data from a specific source into a core tensor that indicates classes centroids, a series of orthogonal factor matrices, and class-indicator factor matrix. Since paired multisource samples should share the same class label, a coupling constraint is imposed on different Tucker models to have a consistent class-indicator factor matrix. Furthermore, to improve the discriminant of the extracted features, a regularization term is constructed to enlarge the difference between core tensors, i.e., increase the difference between class centroids. Then, an alternative optimization strategy is developed to obtain the effective multisource features tensors and the corresponding class label. For CCT-HTD, to extract the valuable and discriminative information contained in multisource heterogeneous data, multiple Tucker models are built to decompose data from different sources into core tensors that indicate class centroids, a series of orthogonal factor matrices, and class-indicator factor matrix. To embed class information into Tucker models, the sum to one constraint and nonnegative constraint is imposed on the factor matrix along with the sample mode so that the value of the corresponding factor matrix can indicate class label. To reduce the distribution discrepancy across sources, the coupling constraint is imposed on different Tucker models to share a consistent core tensor, i.e., encourage samples from different sources to have the closed class centroids. By embedding a self-updating class-indicator factor matrix, the CCT-HTD can learn forwardly the class label of unlabeled samples to make the domain adaptation model work for both supervised and semi-supervised situations. In addition, a regularization term is constructed to ensure the between-class distance can be maximized. Furthermore, by adding an adaptive weighting matrix along with the sample mode, the outliers far from class centroids can be removed to reduce the occurrence of negative transfer [27]. Finally, an alternative optimization scheme is built to obtain effective features across sources. Notably, the proposed C-HTD as a unified framework can effectively solve the problem of multisource heterogeneous feature extraction for domain adaptation and multisource fusion. The contributions of our study can be summarized into the following three aspects:

(1)

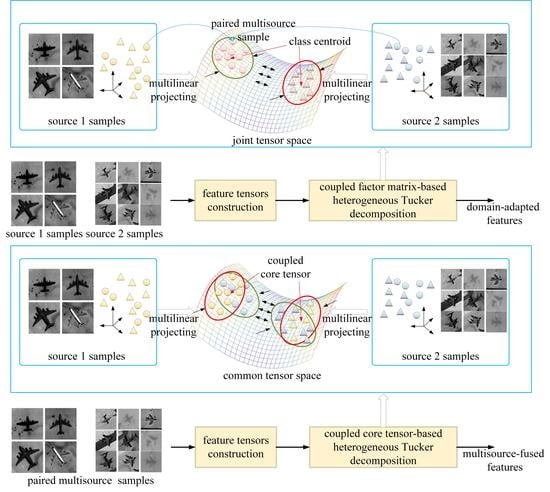
From the perspective of theory, compared with the classical TD and HTD, which can only extract a compressed representation of a single tensor, the proposed C-HTD can be considered a natural extension of the classical TD and HTD that can extract compressed representations of multiple tensors with different dimensions (i.e., heterogeneous tensors) in an associative manner. More importantly, by establishing different coupling constraints, C-HTD can extract complementary information and shared information from the multisource heterogeneous tensors, which dramatically expands the practicability of the TD and HTD techniques;

(2)

From the perspective of the application, compared with the existing multisource fusion-oriented and domain adaptation-oriented feature extraction methods that can only deal with vector or homogeneous tensors, the C-HTD is a unified framework that can deal with multisource fusion-oriented and domain adaptation-oriented feature extraction using multisource heterogeneous tensors directly. In addition, the proposed C-HTD can be applied to both supervised and semi-supervised cases by establishing a class-indicator factor matrix along with sample mode. Moreover, unlike the existing domain adaptation methods that are susceptible to outliers, the CCT-HTD can reduce the impact of outliers on domain adaptation results effectively using an adaptive sample-weighing matrix along with sample mode;

(3)

To ensure the effective implementation of the proposed C-HTD, the alternative optimization scheme is proposed to solve the optimization problems of CFM-HTD and CCT-HTD to obtain the optimal multisource features and the predicted class labels by sequentially updating the core tensors and a series of factor matrices. Additionally, the detailed theoretical analysis provides the convergence and complexity of C-HTD.

The remainder of this study is organized as follows. In Section 2, the used notations, basic tensor algebra, and the conventional TD are introduced briefly. Then, the proposed CFM-HTD and CCT-HTD models are described in detail. In Section 3, the experiments are conducted to compare the proposed CFM-HTD with typical multisource fusion-oriented feature extraction methods and compare the proposed CCT-HTD with typical domain adaptation-oriented feature extraction methods using multiresolution and multiangle optical images dataset, multiangle SAR dataset, and paired optical image and SAR image dataset. Section 4 discusses the experimental results, convergence, and the complexity of the proposed methods. Our conclusion is provided in Section 5.

2. Method

2.1. Preliminaries

Before presenting our work, the notations and fundamental tensor operations, the traditional TD are sequentially introduced in brief.

2.1.1. Notations and Fundamental Tensor Operations

Following the convention in [28], the scalar, vector, matrix, and high-order tensor are denoted as lowercase letters (e.g., x, y), lowercase boldface letters (e.g., x, y), uppercase boldface letters (e.g., M), and calligraphic letters (e.g., $\chi$), respectively. For convenience, the ith entry of vector a, the $\left(i,j\right)$th entry of matrix M, and the $\left(i,j,k\right)$th entry of three-order tensor $\chi \in {ℝ}^{I_1,I_2,I_3}$ are denoted as $a\left(i\right)$, $M\left(i,j\right)$, and $\chi \left(i,j,k\right)$, respectively. In addition, some fundamental tensor operations used in our work are provided as follows:

Definition 1

(Frobenius norm of a tensor $\chi$). The Frobenius norm of a tensor $\chi \in {ℝ}^{I_1,I_2\dots I_N}$ is denoted by ${‖\chi ‖}_F$, as calculated by:

$${‖\chi ‖}_F=\sqrt{{\displaystyle \sum _{i_1,i_2,\dots ,i_N}\chi \left(i_1,i_2,\dots ,i_N\right)\times \chi \left(i_1,i_2,\dots ,i_N\right)}}.$$

(1)

Definition 2

(Mode-k product). The mode-k product of tensor $\chi \in {ℝ}^{I_1,I_2\dots I_N}$ and matrix $\mathit{M}\in {ℝ}^{I_k^{\text{'}},I_k}$is denoted by $y=\chi {\times }_k\mathit{M}$, whose results are a tensor $y\in {ℝ}^{I_1,I_2\dots I_k^{\text{'}}\dots I_N}$, and the value of the entry is defined by:

$$\begin{array}{l}y\left(i_1,i_2,\dots ,i_{k-1},j,i_{k+1},\dots ,i_N\right)=\\ {\displaystyle \sum _{i=1}^{I_k}\chi \left(i_1,i_2,\dots ,i_{k-1},i,i_{k+1},\dots ,i_N\right)\times \mathit{M}\left(j,i\right)}.\end{array}$$

(2)

Definition 3

(Mode-k unfolding). The mode-k unfolding of a tensor $\chi \in {ℝ}^{I_1,I_2\dots I_N}$ denoted as $Ma{t}_{\left(k\right)}\left(\chi \right)$ results in a matrix with dimensions $I_k,{\displaystyle \prod _{j\ne k}{I}_j}$, and the value of the entry is defined by:

$$Ma{t}_{\left(k\right)}\left(\chi \right)\left(i_k,{\displaystyle \sum _{j\ne k}{i}_j\times {\displaystyle \prod _{l=1,l\ne k}^{j-1}{I}_l}}\right)=\chi \left(i_1,\dots ,i_N\right).$$

(3)

2.1.2. Tucker Decomposition

Given a tensor $\chi \in {ℝ}^{I_1,I_2\dots I_N}$, the TD can be formulated as:

$$\underset{{\left\{{\mathit{U}}_n\in \mathbb{S}\left(I_n,i_n\right)\right\}}_{n=1}^N}{\max }{‖\chi {\times }_1{\mathit{U}}_1^T{\times }_2{\mathit{U}}_2^T\dots {\times }_N{\mathit{U}}_N^T‖}_F^2,$$

(4)

where ${\left\{{\mathit{U}}_i^T\right\}}_{i=1}^N$ and $\mathbb{S}\left(I_n,i_n\right)=\left\{\mathit{U}\in {ℝ}^{I_n,i_n},{\mathit{U}}^T\mathit{U}=\mathit{I}\right\}$ ($i_n\le I_n$) denote orthonormal factor matrices and Stiefel manifold containing all rank-d orthonormal bases, respectively. Using the HOSVD [29] or HOOI [30] algorithm, the orthonormal factor matrices can be obtained, and then the core tensor $𝒢\in {ℝ}^{i_1,i_2\dots i_N}$ can be calculated by $𝒢=\chi {\times }_1{\mathit{U}}_1^T{\times }_2{\mathit{U}}_2^T\dots {\times }_N{\mathit{U}}_N^T$. In this way, the Tucker model can be used to decompose the tensor $\chi$ into the core tensor multiplied by a series of factor matrices along with each mode, i.e., $\chi \approx 𝒢{\times }_1{\mathit{U}}_1{\times }_2{\mathit{U}}_2\dots {\times }_N{\mathit{U}}_N$, and the core tensor $𝒢$ can be considered the compressed representation of $\chi$, i.e., the features of $\chi$.

2.2. Coupled Factor Matrix-Based Heterogeneous Tucker Decomposition

To develop the multisource heterogeneous data-oriented feature extraction method for multisource fusion and domain adaptation, the C-HTD method is proposed, including two sub-methods, i.e., CFM-HTD and CCT-HTD, of which the former is used for multisource fusion, and the latter is used for domain adaptation. The illustration of the procedure of the C-HTD is shown in Figure 1.

2.2.1. Motivation

For convenience and without losing the generality, the number of sources is set to two. Given paired multisource remote sensing data, i.e., source 1 sample ${\chi }_1$ and source 2 sample ${\chi }_2$, they can be represented as heterogeneous tensors because data from different sources always present different resolutions and physical properties. Since the existing multisource fusion-oriented feature extraction method can only deal with data represented as vectors or tensors, they fail to process multisource heterogeneous data directly. Due to the complementarity of multisource heterogeneous data, straightforward extraction of heterogeneous features from paired multisource data can mine the multisource information in an associative manner to obtain more accurate object recognition results. In addition, considering the samples may lack class labels, it is necessary for the multisource fusion-oriented feature extraction method to adapt to both the labeled and unlabeled data. To this end, the CFM-HTD method is proposed as follows.

2.2.2. Formulation

Assume that there are N paired multisource samples with M classes ${\left\{{\chi }_1^i,{\chi }_2^i,y^i\right\}}_{i=1}^N$, where ${\chi }_1^i\in {ℝ}^{I_1,I_2,\dots ,I_L}$, ${\chi }_2^i\in {ℝ}^{I_1^{\text{'}},I_2^{\text{'}},\dots ,I_L^{\text{'}}}$, and $y^i\in \left\{0,1,\dots ,M\right\}$ denote the ith sample from source 1, ith sample from source 2, and class label of the ith paired multisource sample, respectively. When $y^i$ is equal to 0, it indicates that the corresponding label is unknown, i.e., unlabeled sample.

Using N samples from source 1 and N samples from source 2, ${\chi }_1=\left[{\chi }_1^1,\dots ,{\chi }_1^N\right]$ and ${\chi }_2=\left[{\chi }_2^1,\dots ,{\chi }_2^N\right]$ can be yielded by cascading them along with the L + 1 order, respectively. To obtain an effective representation of ${\chi }_1$ and ${\chi }_2$, it is necessary to construct two groups of factor matrices $\left\{{\mathit{U}}_1^1\in {ℝ}^{I_1,i_1},\dots ,{\mathit{U}}_L^1\in {ℝ}^{I_L,i_L},{\mathit{U}}_{L+1}^1\in {ℝ}^{N,M}\right\}$ and $\left\{{\mathit{U}}_1^2\in {ℝ}^{I_1^{\text{'}},i_1^{\text{'}}},\dots ,{\mathit{U}}_L^2\in {ℝ}^{I_L^{\text{'}},i_L^{\text{'}}},{\mathit{U}}_{L+1}^2\in {ℝ}^{N,M}\right\}$ along with different modes of ${\chi }_1$ and ${\chi }_2$. Then, similar to TD, the compressed representation of ${\chi }_1$ and ${\chi }_2$ can be calculated by:

$${\chi }_1\approx {𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^1$$

(5)

$${\chi }_2\approx {𝒢}_2{\times }_1{\mathit{U}}_1^2{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^2,$$

(6)

where ${𝒢}_1\in {ℝ}^{i_1,\dots ,i_L,M}$, ${𝒢}_2\in {ℝ}^{i_1,\dots ,i_L,M}$, ${\mathit{U}}_l^1{}^T{\mathit{U}}_l^1=\mathit{I},1\le l\le L$, and ${\mathit{U}}_l^2{}^T{\mathit{U}}_l^2=\mathit{I},1\le l\le L$ denote the core tensor for source 1, core tensor for source 2, orthonormal factor matrices for source 1, and orthonormal factor matrices for source 2, respectively. To utilize the class information of labeled sample, the value of entries of ${\mathit{U}}_{L+1}^1\in {ℝ}^{N,M}$ and ${\mathit{U}}_{L+1}^2\in {ℝ}^{N,M}$ are defined as follows:

$${\mathit{U}}_{L+1}^1\left(i,j\right)=\left\{\begin{array}{l}1 if y^i=j\\ 0 otherwise\end{array}\right.$$

(7)

$${\mathit{U}}_{L+1}^2\left(i,j\right)=\left\{\begin{array}{l}1 if y^i=j\\ 0 otherwise\end{array}\right.$$

(8)

To obtain the class label of unlabeled samples, the sum-to-one constraint and nonnegative constraint are imposed in the ith column of ${\mathit{U}}_{L+1}^1$ and ${\mathit{U}}_{L+1}^2$ corresponding to $y^i=0$, i.e.,

$$\begin{array}{l}{\mathit{U}}_{L+1}^1\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}^1\left(i,j\right)}=1 if y^i=0\\ {\mathit{U}}_{L+1}^2\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}^2\left(i,j\right)}=1 if y^i=0.\end{array}$$

(9)

Since the paired multisource sample shares the same class label, the coupling constraint for ${\mathit{U}}_{L+1}^1$ and ${\mathit{U}}_{L+1}^2$ is constructed to enforce ${\mathit{U}}_{L+1}^1={\mathit{U}}_{L+1}^2$. Therefore, the variable ${\mathit{U}}_{L+1}$ is employed to replace ${\mathit{U}}_{L+1}^1$ and ${\mathit{U}}_{L+1}^2$, and the two Tucker decompositions can be merged as:

$$\begin{array}{l}\underset{{𝒢}_1,{𝒢}_2,{\mathit{U}}_l^1,{\mathit{U}}_l^2,{\mathit{U}}_{L+1}}{\min }{‖{\chi }_1-{𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2+{‖{\chi }_2-{𝒢}_2{\times }_1{\mathit{U}}_1^2{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2\\ s.t.{\mathit{U}}_l^1{}^T{\mathit{U}}_l^1=\mathit{I},1\le l\le L\\ {\mathit{U}}_l^2{}^T{\mathit{U}}_l^2=\mathit{I},1\le l\le L\\ {\mathit{U}}_{L+1}\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}\left(i,j\right)}=1 if y^i=0.\end{array}$$

(10)

Splitting ${𝒢}_1$ and ${𝒢}_2$ along with the $\left(L+1\right)$th order will yield M core sub-tensors, i.e., ${𝒢}_1=\left[{𝒢}_1^1,\dots ,{𝒢}_1^M\right]$ and ${𝒢}_2=\left[{𝒢}_2^1,\dots ,{𝒢}_2^M\right]$, where the mth sub-tensor can be interpreted as the mth class centroid. The value of ${\mathit{U}}_{L+1}\left(i,j\right)$ implies the probability of the ith sample belonging to the jth class. In addition, to enhance the separability of samples with different classes, an intuitive idea is to construct a regularization term maximizing the variance of core sub-tensors to encourage samples of different categories to be as far away as possible. Therefore, Equation (10) can be revised as:

$$\begin{array}{l}\underset{{𝒢}_1,{𝒢}_2,{\mathit{U}}_l^1,{\mathit{U}}_l^2,{\mathit{U}}_{L+1}}{\min }{‖{\chi }_1-{𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2+{‖{\chi }_2-{𝒢}_2{\times }_1{\mathit{U}}_1^2{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2-\\ c\left({\displaystyle \sum _m{‖{𝒢}_1^m-\frac{1}{M}{𝒢}_1{\times }_{L+1}{\mathit{e}}_M‖}_F^2}+{\displaystyle \sum _m{‖{𝒢}_2^m-\frac{1}{M}{𝒢}_2{\times }_{L+1}{\mathit{e}}_M‖}_F^2}\right)\\ s.t.{\mathit{U}}_l^1{}^T{\mathit{U}}_l^1=\mathit{I},1\le l\le L\\ {\mathit{U}}_l^2{}^T{\mathit{U}}_l^2=\mathit{I},1\le l\le L\\ {\mathit{U}}_{L+1}\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}\left(i,j\right)}=1 if y^i=0,\end{array}$$

(11)

where e_M and c denote the vector that all the entries are equal to 1 and the regularization parameter, respectively. Equation (11) is the optimization problem of CFM-HTD. After obtaining the optimal factor matrices, the paired multisource features can be extracted by $y_1^i={\chi }_1^i{\times }_1{\mathit{U}}_1^{1T}{\times }_2\dots {\times }_L{\mathit{U}}_L^{1T}$ and $y_2^i={\chi }_2^i{\times }_1{\mathit{U}}_1^{2T}{\times }_2\dots {\times }_L{\mathit{U}}_L^{2T}$. Meanwhile, the outputted class-indicator matrix ${\mathit{U}}_{L+1}$ can be used to predict the class of unlabeled samples as:

$$y^i=arg\underset{j}{max}{\mathit{U}}_{L+1}\left(i,j\right).$$

(12)

2.2.3. Optimization

To solve the optimization problem of CFM-HTD, the alternative optimization scheme is proposed to update ${\left\{{\mathit{U}}_l^1\right\}}_{l=1}^L$, ${\left\{{\mathit{U}}_l^2\right\}}_{l=1}^L$, ${\mathit{U}}_{L+1}$, ${𝒢}_1$, and ${𝒢}_2$ sequentially.

(a) Updating ${\left\{{\mathit{U}}_l^1\right\}}_{l=1}^L$ and ${\left\{{\mathit{U}}_l^2\right\}}_{l=1}^L$.

Updating ${\left\{{\mathit{U}}_l^1\right\}}_{l=1}^L$ and ${\left\{{\mathit{U}}_l^2\right\}}_{l=1}^L$ is needed to solve the same sub-optimization. For ease of writing, we only provide the updating manner of ${\left\{{\mathit{U}}_l^1\right\}}_{l=1}^L$. When updating ${\left\{{\mathit{U}}_l^1\right\}}_{l=1}^L$, the sub-optimization can be obtained as:

$$\begin{array}{c}\underset{{\mathit{U}}_l^1}{\min }{∥{\chi }_1-{𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}∥}_F^2\hfill \\ s.t.\mathit{U}{{}_l^1}^T{\mathit{U}}_l^1=\mathit{I},1\le l\le L.\end{array}$$

(13)

Equation (13) can be transformed to matrix form Equation (14):

$$\begin{array}{l}\underset{{\mathit{U}}_l^1}{\min }{‖{\mathit{X}}_1^{\left(l\right)}-{\mathit{U}}_l^1{\mathit{G}}_1^{\left(l\right)}{\mathit{H}}_1^{\left(l\right)T}‖}_F^2\\ s.t.{\mathit{U}}_l^1{}^T{\mathit{U}}_l^1=\mathit{I},1\le l\le L,\end{array}$$

(14)

where $X_1^{\left(l\right)}=Ma{t}_{\left(l\right)}\left({\chi }_1\right)$, ${\mathit{G}}_1^{\left(l\right)}=Ma{t}_{\left(l\right)}\left({𝒢}_1\right)$, and ${\mathit{H}}_1^{\left(l\right)}={\mathit{U}}_1^1\otimes \dots {\mathit{U}}_{l-1}^1\otimes {\mathit{U}}_{l+1}^1\otimes \dots {\mathit{U}}_{L+1}$. The operator $\otimes$ denotes the Kronecker product of matrices. Then, Equation (14) can be further revised as:

$$\begin{array}{l}\underset{{\mathit{U}}_l^1}{\min }-tr\left({\mathit{U}}_l^1{\mathit{G}}_1^{\left(l\right)}{\mathit{H}}_1^{\left(l\right)T}{\mathit{X}}_1^{\left(l\right)T}\right)\\ s.t.{\mathit{U}}_l^1{}^T{\mathit{U}}_l^1=\mathit{I},1\le l\le L.\end{array}$$

(15)

Equation (15) is the orthogonal Procrustes problem [31], and it can be solved by:

$${\mathit{U}}_l^1=\widehat{{\mathit{V}}_1}{\widehat{{\mathit{U}}_1}}^T,$$

(16)

where $\widehat{{\mathit{U}}_1}$ and $\widehat{{\mathit{V}}_1}$ denote the left singular vectors of ${\mathit{G}}_1^{\left(l\right)}{\mathit{H}}_1^{\left(l\right)T}{\mathit{X}}_1^{\left(l\right)T}$ and the right singular vectors of ${\mathit{G}}_1^{\left(l\right)}{\mathit{H}}_1^{\left(l\right)T}{\mathit{X}}_1^{\left(l\right)T}$, respectively.

(b) Updating ${\mathit{U}}_{L+1}$.

When updating ${\mathit{U}}_{L+1}$, the current optimization problem can be seen as follows:

$$\begin{array}{l}\underset{{\mathit{U}}_{L+1}}{\min }{‖{\chi }_1-{𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2+{‖{\chi }_2-{𝒢}_2{\times }_1{\mathit{U}}_1^2{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2\\ s.t.{\mathit{U}}_{L+1}\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}\left(i,j\right)}=1 if y^i=0.\end{array}$$

(17)

Since each row in ${\mathit{U}}_{L+1}$ is independent, the updating of ${\mathit{U}}_{L+1}\left(n,:\right)$ for $y^n=0$ can be described as independent sub-optimization, as can be seen below:

$$\begin{array}{l}\underset{{\mathit{U}}_{L+1}\left(n,:\right)}{\min }{‖{\mathit{X}}_1^{n\left(L+1\right)}-{\mathit{U}}_{L+1}\left(n,:\right){\mathit{G}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)T}‖}_F^2+{‖{\mathit{X}}_2^{n\left(L+1\right)}-{\mathit{U}}_{L+1}\left(n,:\right){\mathit{G}}_2^{\left(L+1\right)}{\mathit{H}}_2^{\left(L+1\right)T}‖}_F^2\\ s.t.{\mathit{U}}_{L+1}\left(n,i\right)\ge 0\\ {\displaystyle \sum _i{\mathit{U}}_{L+1}\left(n,i\right)}=1,\end{array}$$

(18)

where ${\mathit{X}}_1^{n\left(L+1\right)}=Ma{t}_{\left(L+1\right)}\left(x_1^n\right)$, ${\mathit{G}}_1^{\left(L+1\right)}=Ma{t}_{\left(L+1\right)}\left({𝒢}_1\right)$, and ${\mathit{H}}_1^{\left(L+1\right)}={\mathit{U}}_1^1\otimes \dots \otimes {\mathit{U}}_L^1$. For convenience, the auxiliary variable $\mathbf{\nu }\in {ℝ}^M$ is constructed, and the Equation (18) can be revised as:

$$\begin{array}{l}\underset{{\mathit{U}}_{L+1}\left(n,:\right)}{\min }{‖{\mathit{X}}_1^{n\left(L+1\right)}-{\mathit{U}}_{L+1}\left(n,:\right){\mathit{G}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)T}‖}_F^2+{‖{\mathit{X}}_2^{n\left(L+1\right)}-{\mathit{U}}_{L+1}\left(n,:\right){\mathit{G}}_2^{\left(L+1\right)}{\mathit{H}}_2^{\left(L+1\right)T}‖}_F^2\\ s.t.\mathbf{\nu }\ge 0\\ {\mathit{U}}_{L+1}\left(n,i\right)=\mathbf{\nu }\left(i\right)\\ {\displaystyle \sum _i{\mathit{U}}_{L+1}\left(n,i\right)}=1.\end{array}$$

(19)

To solve this sub-optimization, utilizing alternating direction method of multipliers [32], the augmented Lagrangian function can be obtained as:

$$\begin{array}{l}\underset{{\mathit{U}}_{L+1}\left(n,:\right)}{\min }{‖{\mathit{X}}_1^{n\left(L+1\right)}-{\mathit{U}}_{L+1}\left(n,:\right){\mathit{G}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)T}‖}_F^2+{‖{\mathit{X}}_2^{n\left(L+1\right)}-{\mathit{U}}_{L+1}\left(n,:\right){\mathit{G}}_2^{\left(L+1\right)}{\mathit{H}}_2^{\left(L+1\right)T}‖}_F^2+\\ \frac{\mu }{2}{‖{\displaystyle \sum _i{\mathit{U}}_{L+1}\left(n,i\right)}-1‖}_2^2+{\displaystyle \sum _i\frac{\mu }{2}{‖{\mathit{U}}_{L+1}\left(n,i\right)-\mathbf{\nu }\left(i\right)‖}_2^2}+\\ \lambda \left({\displaystyle \sum _i{\mathit{U}}_{L+1}\left(n,i\right)}-1\right)+{\displaystyle \sum _i{\mathbf{\lambda }}^{\prime }\left(i\right)\left({\mathit{U}}_{L+1}\left(n,i\right)-\mathbf{\nu }\left(i\right)\right)}\\ s.t.\mathbf{\nu }\ge 0,\end{array}$$

(20)

where $\mu$ denotes the penalty parameter. The $\lambda$ and ${\mathbf{\lambda }}^{\text{'}}$ are Lagrangian multipliers. The partial derivative with respect to ${\mathit{U}}_{L+1}\left(n,:\right)$ are zeros. We have:

$$\begin{array}{l}\frac{\partial ℒ}{\partial {\mathit{U}}_{L+1}\left(n,:\right)}=0\Rightarrow \\ {\mathit{U}}_{L+1}{\left(n,:\right)}^T={\left(2{\mathit{G}}_1^{\left(L+1\right)}{\mathit{G}}_1^{\left(L+1\right)T}+2{\mathit{G}}_2^{\left(L+1\right)}{\mathit{G}}_2^{\left(L+1\right)T}+\mu \mathit{e}{\mathit{e}}^T+\mu \times diag\left(\mathit{e}\right)\right)}^{-1}\times \\ (2{\mathit{G}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)T}{\mathit{X}}_1^{n\left(L+1\right)T}+2{\mathit{G}}_2^{\left(L+1\right)}{\mathit{H}}_2^{\left(L+1\right)T}{\mathit{X}}_2^{n\left(L+1\right)T}+\mu \left(\mathit{e}+\mathbf{\nu }\right)-\lambda \mathit{e}-{\mathbf{\lambda }}^{\text{'}}).\end{array}$$

(21)

According to Equation (21), ${\mathit{U}}_{L+1}\left(n,:\right)$ can be updated. For $\lambda$ and ${\mathbf{\lambda }}^{\text{'}}$, they can be updated by:

$$\begin{array}{l}\lambda =\lambda +\mu \left({\displaystyle \sum _i{\mathit{U}}_{L+1}\left(n,i\right)}-1\right)\\ {\mathbf{\lambda }}^{\text{'}}\left(i\right)={\mathbf{\lambda }}^{\text{'}}\left(i\right)+\mu \left({\mathit{U}}_{L+1}\left(n,i\right)-\mathbf{\nu }\left(i\right)\right).\end{array}$$

(22)

For $\mathbf{\nu }$, let the partial derivative of the objective function in Equation (20) with respect to $\mathbf{\nu }$ be zeros. We have:

$$\begin{array}{l}\frac{\partial ℒ}{\partial \mathbf{\nu }\left(i\right)}=0\Rightarrow \\ \mathbf{\nu }\left(i\right)=\frac{1}{\mu }\left(\mu {\mathit{U}}_{L+1}\left(n,i\right)+{\mathbf{\lambda }}^{\text{'}}\left(i\right)\right).\end{array}$$

(23)

Combining with the nonnegative constraint, the $\mathbf{\nu }$ can be updated as:

$$\mathbf{\nu }\left(i\right)=max\left(0,\frac{1}{\mu }\left(\mu {\mathit{U}}_{L+1}\left(n,i\right)+{\mathbf{\lambda }}^{\text{'}}\left(i\right)\right)\right).$$

(24)

As to $\mu$, it is updated by the following manner.

$$\mu =min\left(p\mu ,{\mu }_{max}\right),$$

(25)

where p and ${\mu }_{max}$ denote the learning rate and the upper bound of the penalty parameter, respectively.

(c) Updating ${𝒢}_1$ and ${𝒢}_2$.

Updating ${𝒢}_1$ and ${𝒢}_2$ is needed to solve a similar optimization problem. For ease of writing, we only provide the updating procedure of ${𝒢}_1$. Likewise, the ${𝒢}_2$ can be updated in the same way.

When updating ${𝒢}_1$, the following sub-optimization is needed to be solved.

$$\underset{{𝒢}_1}{\min }{‖{\delta }_1-{𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2-c\cdot \left({\displaystyle \sum _m{‖{𝒢}_1^m-\frac{1}{M}{𝒢}_1{\times }_{L+1}{\mathit{e}}_M‖}_F^2}\right).$$

(26)

Converting Equation (26) to matrix form, we have:

$$\underset{{𝒢}_1}{\min }{‖{\mathit{X}}_1^{\left(L+1\right)}-{\mathit{U}}_{L+1}\times {\mathit{G}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)T}‖}_F^2+tr\left({\mathit{G}}_1^{\left(L+1\right)T}\mathit{L}{\mathit{G}}_1^{\left(L+1\right)}\right)$$

(27)

where ${\mathit{X}}_1^{\left(L+1\right)}=Ma{t}_{\left(L+1\right)}\left(x_1\right)$, ${\mathit{G}}_1^{\left(L+1\right)}=Ma{t}_{\left(L+1\right)}\left({𝒢}_1\right)$, and ${\mathit{H}}_1^{\left(L+1\right)}={\mathit{U}}_1^1\otimes \dots \otimes {\mathit{U}}_L^1$. $\mathit{L}$ is the Laplacian matrix, and the detailed definition is shown below.

$$\begin{array}{l}\mathit{L}=-c\left({\displaystyle \sum _{m=1}^M{\tilde{\mathit{e}}}_m}{\tilde{\mathit{e}}}_m^T\right)\\ {\tilde{\mathit{e}}}_m\in {ℝ}^M\\ {\tilde{\mathit{e}}}_m\left(i\right)=\left\{\begin{array}{l}1-\frac{1}{M} if i=m\\ -\frac{1}{M} if i\ne m.\end{array}\right.\end{array}$$

(28)

To update each row of ${\mathit{G}}_1^{\left(L+1\right)}$, the partial derivative of Equation (28) with respect to ${\mathit{G}}_1^{\left(L+1\right)}\left(i,:\right)$ is set with zeros. We have:

$${\mathit{G}}_1^{\left(L+1\right)}\left(i,:\right)={\left(\widehat{\mathit{U}}\left(i,i\right)+\mathit{L}\left(i,i\right)\right)}^{-1}\times \left(-{\mathit{U}}_{L+1}{\left(:,i\right)}^T{\mathit{X}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)}-{\mathit{l}}^T\times {\mathit{G}}_1^{\left(L+1\right)}\right),$$

(29)

where $\widehat{\mathit{U}}={\mathit{U}}_{L+1}{}^T{\mathit{U}}_{L+1}$. The $\mathit{l}\in {ℝ}^M$ defined by $\mathit{l}=\mathit{L}\left(:,i\right)+\widehat{\mathit{U}}\left(:,i\right),\mathit{l}\left(i\right)=0$.

Using Equation (29), the ${\mathit{G}}_1^{\left(L+1\right)}\left(i,:\right)$ can be updated.

The variables ${\left\{{\mathit{U}}_l^1\right\}}_{l=1}^L$, ${\left\{{\mathit{U}}_l^2\right\}}_{l=1}^L$, ${\mathit{U}}_{L+1}$, ${𝒢}_1$, and ${𝒢}_2$ are updated iteratively until the iteration number exceeds the threshold or the following terminal criteria are met.

$${\displaystyle \sum _{l=1}^L{‖{\mathit{U}}_l^1-{\widehat{\mathit{U}}}_l^1‖}_F^2}+{\displaystyle \sum _{l=1}^L{‖{\mathit{U}}_l^2-{\widehat{\mathit{U}}}_l^2‖}_F^2}\le \delta ,$$

(30)

where ${\widehat{\mathit{U}}}_l^1$ and ${\widehat{\mathit{U}}}_l^2$ denote the factor matrices updated in the last iteration.

2.3. Coupled Core Tensor-Based Heterogeneous Tucker Decomposition

2.3.1. Motivation

For ease of writing and without losing generality, the number of sources is set to 2. Assume that we have source 1 data $\left\{{\chi }_s,y_s\right\}$ and source 2 data $\left\{{\chi }_t,y_t\right\}$ acquired from different sensors, where ${\chi }_s$, $y_s$, ${\chi }_t$, and $y_t$ denote the sample from source 1, the class label of sample from source 1, the sample from source 2, and the class label of sample from source 2, respectively. Often, ${\chi }_s$ and ${\chi }_t$ present different dimensions, i.e., heterogeneous tensors. Not only that, since ${\chi }_s$ and ${\chi }_t$ present different physical properties, they obey different margin distributions $P\left({\chi }_s\right)\ne P\left({\chi }_t\right)$ and different class condition distributions $P\left({\chi }_s|y_s\right)\ne P\left({\chi }_t|y_t\right)$. To achieve object recognition across sources, it is necessary to construct a domain adaptation method to construct specific mapping $\phi \left(\cdot \right)$, making $P\left(\phi \left({\chi }_s\right)|y_s\right)\approx P\left(\phi \left({\chi }_t\right)|y_t\right)$. In addition, considering that the class labels of some samples are unknown, the domain adaptation method should have the ability to predict the class label of these samples and then use predicted labels ${\widehat{y}}_s,{\widehat{y}}_t$ to make $P\left(\phi \left({\chi }_s\right)|{\widehat{y}}_s\right)\approx P\left(\phi \left({\chi }_t\right)|{\widehat{y}}_t\right)$. Moreover, to avoid the occurrence of negative transfer, the constructed domain adaptation method should be able to automatically remove outliers to improve the robustness of the extracted features.

2.3.2. Formulation

Assume that we have source domain samples ${\left\{{\chi }_s^i,y_s^i\right\}}_{i=1}^{N_s}$ acquired from source 1 and target domain samples ${\left\{{\chi }_t^i,y_t^i\right\}}_{i=1}^{N_t}$ acquired from source 2, where ${\chi }_s^i\in {ℝ}^{I_1,I_2,\dots ,I_L}$, $y_s^i\in \left\{0,1,\dots ,M\right\}$, ${\chi }_t^i\in {ℝ}^{I_1^{\text{'}},I_2^{\text{'}},\dots ,I_L^{\text{'}}}$, and $y_s^i\in \left\{0,1,\dots ,M\right\}$ denote the ith sample from source domain, the class label of the ith sample from source domain, the ith sample from target domain, the class label of the ith sample from target domain, respectively. The dimensions of source domain sample and target domain sample may be different, i.e., $I_l\ne I_l^{\text{'}}$. When $y_s^i=0$ or $y_t^i=0$, it implies that the corresponding sample is unlabeled.

The intention of the proposed method is to find factor matrices with different modes of source domain data ${\left\{{\mathit{U}}_l^s\in {ℝ}^{I_l,i_l}\right\}}_{l=1}^L$ and factor matrices with different modes ${\left\{{\mathit{U}}_l^t\in {ℝ}^{I_l^{\text{'}},i_l}\right\}}_{l=1}^L$ of target domain data to map the input of heterogeneous tensors into the shared space. To achieve this goal, the $\left(L+1\right)$th order tensor ${\chi }_s$ is constructed by cascading samples from source domain $[{\chi }_s^1,\dots ,{\chi }_s^{N_s}]$, and the $\left(L+1\right)$th order tensor ${\chi }_t$ is constructed by cascading samples $\left[{\chi }_t^1,\dots ,{\chi }_t^{N_t}\right]$ from the target domain. Similar to TD, the compressed representation of ${\chi }_s$. and ${\chi }_t$ can be obtained as follows:

$${\chi }_s\approx {𝒢}_s{\times }_1{\mathit{U}}_1^s{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^s$$

(31)

$${\chi }_t\approx {𝒢}_t{\times }_1{\mathit{U}}_1^t{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^t,$$

(32)

where ${𝒢}_s\in {ℝ}^{i_1,\dots ,i_L,M}$ and ${𝒢}_t\in {ℝ}^{i_1,\dots ,i_L,M}$ denote the core tensor of the source domain and core tensor of the target domain, respectively. The ${\left\{{\mathit{U}}_l^s\right\}}_{l=1}^L$ and ${\left\{{\mathit{U}}_l^t\right\}}_{l=1}^L$ are orthogonal factor matrices satisfying constraints ${\mathit{U}}_l^s{}^T{\mathit{U}}_l^s=\mathit{I},1\le l\le L$ and ${\mathit{U}}_l^t{}^T{\mathit{U}}_l^t=\mathit{I},1\le l\le L$. The ${\mathit{U}}_{L+1}^s\in {ℝ}^{N_s,M}$ and ${\mathit{U}}_{L+1}^t\in {ℝ}^{N_t,M}$ can be interpreted as the class-indicator matrix. For labeled samples ${\chi }_s^i$(${\chi }_t^i$), if $y_s^i=j$ ($y_t^i=j$), let ${\mathit{U}}_L^s\left(i,j\right)=1$ (${\mathit{U}}_L^t\left(i,j\right)=1$) and ${\mathit{U}}_L^s\left(i,k\right)=0,k\ne j$ (${\mathit{U}}_L^t\left(i,k\right)=0,k\ne j$). For unlabeled samples, the constraints for the class-indicator factor matrix are constructed as follows:

$$\begin{array}{l}{\mathit{U}}_L^s\left(i,:\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_L^s\left(i,j\right)}=1 if y_s^i=0\\ {\mathit{U}}_L^t\left(i,:\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_L^t\left(i,j\right)}=1 if y_t^i=0.\end{array}$$

(33)

To calculate the effective factor matrices and core tensor, the following objective function is constructed:

$$\underset{{𝒢}_s,{𝒢}_t,{\mathit{U}}_l^s,{\mathit{U}}_l^t}{\min }{‖{\chi }_s-{𝒢}_s{\times }_1{\mathit{U}}_1^s{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^s‖}_F^2+{‖{\chi }_t-{𝒢}_t{\times }_1{\mathit{U}}_1^t{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^t‖}_F^2.$$

(34)

Note that the dimension of ${𝒢}_s$ or ${𝒢}_t$ in mode $\left(L+1\right)$ is equal to M. Therefore, the ${𝒢}_s$ or ${𝒢}_t$ can be split into M sub-tensors along with mode $\left(L+1\right)$, i.e., ${𝒢}_s=\left[{𝒢}_s^1,\dots ,{𝒢}_s^M\right]$ and ${𝒢}_t=\left[{𝒢}_t^1,\dots ,{𝒢}_t^M\right]$, where ${𝒢}_s^m$ and ${𝒢}_t^m$ can be interpreted as the class centroid of the source domain and target domain, respectively. In addition, there may exist some samples from the source domain that present poor quality and thus are not suitable for transferring, i.e., there may exist outliers for source domain data. To solve this problem, the adaptive sample-weighing matrix for the source domain ${\mathit{W}}^s\in {ℝ}^{N_s,N_s}$ is constructed to remove outliers automatically and embedded into the optimization problem, as shown below:

$$\begin{array}{l}\underset{{𝒢}_s,{𝒢}_t,{\mathit{U}}_l^s,{\mathit{U}}_l^t,{\mathit{W}}^s,{\mathit{W}}^t}{\min }{‖{\chi }_s{\times }_{L+1}{\mathit{W}}^s-{𝒢}_s{\times }_1{\mathit{U}}_1^s{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^s{\times }_{L+1}{\mathit{W}}^s‖}_F^2+{‖{\chi }_t-{𝒢}_t{\times }_1{\mathit{U}}_1^t{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^t‖}_F^2\\ s.t.{\displaystyle \sum _i{\mathit{W}}^s{\left(i,i\right)}^2}=\left(1-{\epsilon }_s\right)N_s\\ {\mathit{W}}^s\left(i,j\right)=0 \forall i\ne j\\ 0\le {\mathit{W}}^s{\left(i,i\right)}^2\le 1,\end{array}$$

(35)

where ${\epsilon }_s$ denotes a pre-established constant used to determine the ratio of outliers. It is observed that the adaptive sample-weighing matrix ${\mathit{W}}^s\in {ℝ}^{N_s,N_s}$ is a diagonal matrix, and the value of ${\mathit{W}}^s\left(i,j\right)$ is used to determine the weight of ${\chi }_s^i$.

For domain adaptation problems, it is required that samples from different domains have similar class condition distributions. Therefore, the intuitive idea is to construct the coupled constraint for ${𝒢}_s$ and ${𝒢}_t$, i.e., imposing $𝒢={𝒢}_s={𝒢}_t$. Consequently, the objective function is transformed as:

$$\underset{𝒢,{\mathit{U}}_l^s,{\mathit{U}}_l^t,{\mathit{W}}^s,{\mathit{W}}^t}{\min }{‖{\chi }_s{\times }_{L+1}{\mathit{W}}^s-𝒢{\times }_1{\mathit{U}}_1^s{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^s{\times }_{L+1}{\mathit{W}}^s‖}_F^2+{‖{\chi }_t-𝒢{\times }_1{\mathit{U}}_1^t{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^t‖}_F^2.$$

(36)

To improve the separability of the domain-adapted features, it is necessary to increase the difference between the sub-core tensor of different categories, i.e., maximizing ${\displaystyle \sum _m{‖{𝒢}^m-\frac{1}{M}𝒢{\times }_{L+1}{\mathit{e}}_M‖}_F^2}$, where $𝒢=\left[{𝒢}^1,\dots ,{𝒢}^M\right]$ and ${\mathit{e}}_M=\underset{M}{\underbrace{\left[1,\mathrm{1...1}\right]}}$. By integrating this term, the optimization problem of CCT-HTD can be obtained as follows:

$$\begin{array}{l}\underset{𝒢,{\mathit{U}}_l^s,{\mathit{U}}_l^t,{\mathit{W}}^s}{\min }{‖{\chi }_s{\times }_{L+1}{\mathit{W}}^s-𝒢{\times }_1{\mathit{U}}_1^s{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^s{\times }_{L+1}{\mathit{W}}^s‖}_F^2+\\ {‖{\chi }_t-𝒢{\times }_1{\mathit{U}}_1^t{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^t‖}_F^2-c\times \left({\displaystyle \sum _m{‖{𝒢}^m-\frac{1}{M}𝒢{\times }_{L+1}{\mathit{e}}_M‖}_F^2}\right)\\ s.t.{\displaystyle \sum _i{\mathit{W}}^s{\left(i,i\right)}^2}=\left(1-{\epsilon }_s\right)N_s\\ {\mathit{W}}^s\left(i,j\right)=0 \forall i\ne j\\ 0\le {\mathit{W}}^s{\left(i,i\right)}^2\le 1\\ {\mathit{U}}_l^{sT}{\mathit{U}}_l^s=\mathit{I} 1\le l\le L\\ {\mathit{U}}_l^{tT}{\mathit{U}}_l^t=\mathit{I} 1\le l\le L\\ {\mathit{U}}_{L+1}^s\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}^s\left(i,j\right)}=1if y_s^i=0\\ {\mathit{U}}_{L+1}^t\left(i,j\right)\ge 0 {\displaystyle \sum _j{\mathit{U}}_{L+1}^t\left(i,j\right)}=1if y_t^i=0,\end{array}$$

(37)

where c denotes the regularization parameter. The optimization solving method of CCT-HTD is similar to that of CFM-HTD, with no more tautology here. The detailed optimization solving processing can be seen in Appendix A. After obtaining the optimal factor matrices, the domain-adapted features can be extracted by $y_s^i={\chi }_s^i{\times }_1{\mathit{U}}_1^{sT}{\times }_2\dots {\times }_L{\mathit{U}}_L^{sT}$ and $y_t^i={\chi }_t^i{\times }_1{\mathit{U}}_1^{tT}{\times }_2\dots {\times }_L{\mathit{U}}_L^{tT}$.

3. Results

To evaluate the performance of the C-HTD for multisource fusion and domain adaptation, three datasets were built to examine the effect of proposed CFM-HTD and CCT-HTD compared with typical multisource fusion-oriented feature extraction methods and domain adaptation-oriented feature extraction methods, respectively.

The experiments consist of six parts. In Section 3.1, the information of the used datasets is introduced in detail. In Section 3.2, the construction of heterogeneous tensors for multisource data is described. The performance and parameter setting of CFM-HTD and CCT-HTD are analyzed in Section 3.3 and Section 3.4, respectively. In Section 3.5, the performance of CFM-HTD is evaluated compared with typical multisource fusion-oriented feature extraction methods. In Section 3.6, the performance of CCT-HTD is evaluated compared with typical domain adaptation-oriented feature extraction methods.

All the simulations were executed on a computer with a Windows 10 operating system equipped with a CPU of I7-7700 processor at 3.6 GHz.

Our code can be found at Supplementary Material https://github.com/supergt3/C-HTD (accessed on 1 May 2022).

3.1. Datasets

The detailed information of the used datasets is provided below.

(1) Dataset 1 comprises optical airplane slices with different resolutions and different angles acquired from SuperView-1 commercial satellites with 0.5-m spatial resolution and roll satellite angles less than 20° and Jilin-1 commercial satellites with 1 m spatial resolution and roll satellite angles exceeding 20°. These airplane slices were cut from four RSIs, and the detailed information of these RSIs is provided in

Table 1. Detailed information of used remote sensing images acquired from different satellites.

Satellite	Roll Angle	Resolution	Acquired Time
SuperView-1	−2.79°	0.5 m	9 February 2020
SuperView-1	−13.62°	0.5 m	30 July 2020
Jilin-1	33.11°	1 m	7 October 2020
Jilin-1	−34.20°	1 m	7 November 2020

.

Since these airplane slices were obtained from different satellites, they were divided into two sub-datasets for domain adaptation, where sub-dataset 1 (i.e., source domain samples) contains 36 airplane slices with three types obtained from SuperView-1 commercial satellites, and the sub-dataset 2 (i.e., target domain samples) contains 65 airplane slices with three types obtained from Jilin-1 commercial satellites. In addition, since the SuperView-1 satellite and Jilin-1 satellite observe the same airport area, some airplanes are observed by both two satellites producing 28 paired multisource airplane slices with three types that can be used for multisource fusion-oriented object recognition. The examples of image slices in dataset 1 are displayed in Figure 2.

(2) Dataset 2 consists of SAR slices obtained from the Moving and Stationary Target Acquisition and Recognition (MSTAR) dataset [33]. These SAR slices present the 0.3-m spatial resolution, 17° of depression angle, and aspect angle ranging from 0 to 360°, were collected from X-band and contain five types of ground targets, i.e., 2S1-B01 rocket launcher, BRDM2 armored personnel carriers, T62 tank, ZIL131 truck, and T72 tank. Since the MSTAR dataset contains SAR slices with different aspect angles, we selected SAR slices with a large difference in aspect angles to build two sub-datasets for domain adaptation and multisource fusion, where sub-dataset 1 (i.e., source domain samples) contains 177 SAR slices with aspect angles ranging from 0 to 45° and sub-dataset 2 (i.e., target domain samples) contains 177 SAR slices with aspect angle ranging from 180 to 225°. In addition, combining the SAR slices of the two sub-datasets in pairs, 177 paired multiangle SAR slices can be obtained for multisource fusion tasks. The examples of target slices in dataset 2 are provided in Figure 3.

(3) Dataset 3 consists of 31 paired optical ship slices and SAR ship slices of four types, which were collected from Google Earth images and Terra SAR satellite images observing the same harbor region. Both the optical ship slices and SAR ship slices present 1-m spatial resolution. When performing the domain adaptation test, the optical slices and SAR slices were considered as source domain samples and target domain samples, respectively. The examples of paired optical ship slices and SAR ship slices are displayed in Figure 4.

3.2. Construction of Heterogeneous Tensors

The dataset used in the experiment contains optical image slices and SAR image slices. To describe the object information contained in different sources effectively, the optical features tensor and SAR features tensor are constructed using the different image descriptors, which can be used as input to examine the performance of feature extraction methods. The detailed features tensor construction method is as follows.

Gabor features tensor: Gabor features [34], similar to the conventional image features, can be used to describe the texture characteristics of different scales and orientations utilizing Gabor filters, as calculated by:

$$G_{s,d}\left(x,y\right)=G_{\overrightarrow{\kappa }}\left(\overrightarrow{x}\right)=\frac{‖\overrightarrow{\kappa }‖}{{\sigma }^2}\cdot e^{-\frac{{‖\overrightarrow{\kappa }‖}^2\cdot {‖\overrightarrow{x}‖}^2}{2{\sigma }^2}}\cdot e^{i\overrightarrow{\kappa }\cdot \overrightarrow{x}}-e^{-\frac{{\sigma }^2}{2}},$$

(38)

where $\overrightarrow{x}=\left(x,y\right)$ and $\overrightarrow{\kappa }=\left(\pi /2\times 2^s\right)\cdot \left[\cos \left(\frac{\pi d}{8}\right),\sin \left(\frac{\pi d}{8}\right)\right]$ denote the spatial domain coordinate and the frequency vector, respectively. In our experiments, the scale parameter s and the orientation parameter d were set to $\left\{1,2,3,4\right\}$ and $\left\{1,2,3,4,5,6,7,8\right\}$, respectively, to obtain 32 Gabor filters. The Gabor features are extracted and stored to the 3rd-order Gabor features tensor $F_{𝒢abor}\in {ℝ}^{w\times h\times 32}$.

Spectral features tensor: the raw optical image slice as the spectral features tensor is used $F_{ori}\in {ℝ}^{w\times h\times 3}$, where the third-order denotes the spectral order.

Morphology features tensor: to emphasize partial detailed information contained in slices, the top-hat transform and bottom-hat transform [35] for morphology processing are used to generate morphology features stored as feature tensors $F_{mori}\in {ℝ}^{w\times h\times 2}$.

The features tensor of the optical image slice can be obtained by concatenating the Gabor feature tensor, the spectral feature tensor, and the morphological feature tensor along with the third mode, i.e., ${ℱ}_{optical}=\left[{ℱ}_{𝒢abor},{ℱ}_{ori},{ℱ}_{mori}\right]$.

The scattering characteristic [36,37] of SAR images reflecting the structure and material property of objects can be considered important parameters. To extract scattering characteristics of SAR images effectively, the gray-level cooccurrence matrices (GLCMs) [35] with 14 different scanning directions for pair pixels are utilized to construct the SAR feature tensor ${ℱ}_{sar}\in {ℝ}^{8\times 8\times 14}$, where the dimensions of the first order and second order denote the quantized gray level of the GLCM features.

3.3. Analysis of the Impact of Parameter Setting on CFM-HTD

For CFM-HTD, there are only a few manually set parameters, including the iteration number threshold and the regularization parameter c. To analyze the impact of parameter setting on CFM-HTD, paired multiresolution multiangle airplane slices in dataset 1 are utilized to verify the classification results of CFM-HTD under different parameter settings. First, the ratio of labeled samples in dataset 1 is set to 50%, and all samples in dataset 1 are fed into CFM-HTD to learn the labels of the unlabeled samples. Then, the objective function values and classification accuracies of CFM-HTD under different iteration numbers are recorded, as shown in Figure 5.

From Figure 4, it is observed that the objective function value decreases and accuracy increases as the increase in iteration numbers. Specifically, the objective function value and accuracy change dramatically after initial iterations. When the number of iterations reaches six or more, the accuracy and objective function value becomes stable and converge. This finding indicates that the proposed CFM-HTD can converge and obtain better classification results after a few iterations.

In addition to regularization parameter c, considering CFM-HTD as a semi-supervised feature extraction method, its performance is affected by the ratio of labeled samples. To analyze the impact of regularization parameter c and the ratio of labeled samples, experiments were conducted on dataset 1 to compare the classification accuracy under different regularization parameters c and different ratios of labeled samples. The results are shown in Figure 6.

From the above figure, it can be found that the classification accuracy of CFM-HTD is relatively poor when the ratio of labeled samples is less than 0.3. As the ratio of labeled samples increases, the classification accuracy of CFM-HTD can be remarkably improved. In particular, CFM-HTD can obtain the best classification accuracy when the ratio of labeled samples exceeds 0.5. In addition, it can be found that different regularization parameters have an insignificant impact on the results of CFM-HTD. With the increase in the labeled samples, CFM-HTD can obtain the best classification results under different regularization parameters c.

3.4. Analysis of the Impact of Parameter Setting on CCT-HTD

The optimization solving scheme of CCT-HTD is an iterative process that successively updates the values of the factor matrix and the core tensor. To illustrate the impact of the number of iterations on the performance of CCT-HTD, the experiments used dataset 1 to compare the cross-domain classification ability of CCT-HTD under different numbers of iterations. Concretely, sub-dataset 1 and sub-dataset 2 of dataset 1 are regarded as the source domain and target domain, respectively. Then different iteration numbers were set for CCT-HTD to obtain domain-adapted features. To verify classification accuracy across domains, the one nearest neighbor (1NN) classifier trained by samples from the source domain is applied to obtain the classification accuracy of the target domain. The detailed results are shown in Figure 7.

It is observed in Figure 7 that the objective function value decreases and accuracy increases as the iteration processing. After a few iterations, the objective function value and classification accuracy tend to be stable and converge.

In addition, the proposed CCT-HTD method as a semi-supervised domain adaptation method is able to combine labeled samples with unlabeled samples to learn features across domains jointly. To demonstrate the impact of the ratio of labeled samples on the domain adaptation results, CCT-HTD was executed by adjusting the ratio of labeled samples to obtain the domain adaptation-oriented features. Then, the 1NN classifier was trained using the source domain samples, and the classification results of the target domain samples were obtained, as shown in Figure 8.

Figure 8 shows the accuracy of CCT-HTD with different parameters c under different ratios of labeled samples to the total samples. It can be found that the classification accuracy across domains increases first and then has a slight decrease as the number of labeled samples increases. The reason is that when the number of labeled samples is too small, CCT-HTD cannot accurately estimate the class of unlabeled samples. When the number of labeled samples is too large, the hard labels cannot fully reflect the category affiliation of the data compared with the fuzzy labels learned by CCT-HTD autonomously. It was found that the best results can be obtained when the ratio of labeled samples is between 0.6 and 0.8. In addition, it was also found that the impact of different parameter c on classification accuracy is slight.

For the CCT-HTD, its main pre-determined parameters include the extracted feature dimension, the regularization parameter c, and the parameter $\epsilon$ that controls the ratio of outliers. To show the impact of different parameter settings on CCT-HTD, the experiments were conducted on dataset 1 to obtain cross-domain feature extraction results of CCT-HTD under different parameter settings. Then, the source domain samples were used for training the one nearest neighbor (1NN) classifier, and target domain samples were used as the test set to obtain the classification accuracy. The results are shown in Figure 9.

The horizontal coordinate j indicates the dimension of extracted features tensor $I_m^{\text{'}}=ceil\left(\frac{I_m}{j}\right)$. As seen in Figure 9, CCT-HTD obtains different accuracies for different dimensions of extracted features tensor, different c, and different $\epsilon$, respectively. In detail, CCT-HTD obtains better results when $I_m^{\text{'}}=ceil\left(\frac{I_m}{6}\right)$ probably because larger feature dimensions tend to obtain redundant features and lower feature dimensions tend to lose critical information across domains. In addition, it can be seen that the impact of different parameters c on the classification results is not apparent. For the parameters $\epsilon$, a larger parameter $\epsilon$ loses more valuable samples, while in a smaller parameter $\epsilon$ it is difficult to remove outlier completely. It can be found that $\epsilon =0.1$ leads to better results.

The CCT-HTD can exploit the adaptive sample-weighing matrix to remove outliers to reduce the occurrence of negative transfer. To demonstrate this advantage visually, sub-dataset 1 and 2 in dataset 2 were regarded as the source domain and target domain, respectively, and three interference samples with aspect angle ranging from 90 to 135° were added into the source domain. Then, the 2D-projection of original samples and domain-adapted samples by applying the t-SNE [38] method is shown in Figure 10.

It is seen that the original samples are arranged in a more disorganized way due to the differences between different domains and differences between different sources. After applying CCT-HTD, it can be found that the data from two categories form two clusters with better separability and fewer differences between samples from the same category in the source and target domains. Observing Figure 10, it is seen that CCT-HTD can spontaneously find outliers and remove them accurately.

3.5. Evaluation of the Performance of CFM-HTD Compared with Typical Multisource Fusion Methods

The CFM-HTD can excavate the complementary features from paired multisource samples and output the class labels. To evaluate the performance of CFM-HTD, two datasets were utilized to compare CFM-HTD with typical feature extraction methods, including PCA, LLE [39], LE [40], MPCA, HTD, GTDA, TLPP, and TDLA. For vector-based feature extraction methods, i.e., PCA, LLE, and LE, since they can only process inputs characterized as vectors, the constructed multisource features tensors were vectorized to meet their input requirements. For tensor-based comparison methods, i.e., MPCA, GTDA, HTD, TLPP, and TDLA, since they can only process homogeneous tensors, samples from different sources were processed independently to obtain feature extraction results. To comprehensively evaluate the performance of the proposed CFM-HTD method, the experiment verifies the performance of different methods from the perspectives of classification and clustering. For classification performance, we used classification accuracy (ACC) to evaluate different methods. For cluster performance, it was evaluated using normalized mutual information (NMI), as calculated by:

$$NMI\left(\widehat{\mathit{y}},\mathit{y}\right)=\frac{MI\left(\widehat{\mathit{y}},\mathit{y}\right)}{\max \left(H\left(\widehat{\mathit{y}}\right),H\left(\mathit{y}\right)\right)}$$

(39)

where $\widehat{\mathit{y}}$ and $\mathit{y}$ denote the predicted class labels and the real class labels, respectively. The operator $MI\left(\cdot \right)$ and $H\left(\cdot \right)$ denote mutual information and entropy, respectively.

For the comparison method, the extracted features are classified by the SVM classifier to calculate the ACC and clustered by the KM method to calculate the NMI; for the proposed CFM-HTD, the clustering results were obtained by the KM method to calculate the NMI. Since CFM-HTD can output class labels, it can directly test ACC. To facilitate a fair comparison, when evaluating the classification accuracy, the comparison method uses half of the samples in the dataset for training and the rest samples for testing, and the CFM-HTD method uses half of the samples in the dataset as labeled samples and the rest as unlabeled samples. When calculating NMI, the KM method was performed five times, and then the best results were selected as the final NMI. To obtain the best results for different methods, all the vector-based methods set dimensions of extracted features from $\left\{10,20,\dots ,100\right\}$ corresponding to the best results, and all the tensor-based methods set dimensions of extracted features from $I_m^{\text{'}}=ceil\left(\frac{I_m}{j}\right),j\in \left\{2,3,\dots ,8\right\}$ corresponding to the best results. Utilizing three datasets, the obtained experimental results are shown in

Table 2. ACC and NMI of different multisource fusion methods using dataset 1.

	PCA	LLE	LE	MPCA	HTD	GTDA	TLPP	TDLA	CFM-HTD
NMI	0.769	0.184	0.200	0.8633	0.7981	0.8827	0.7984	0.8827	1
ACC	0.75	0.6071	0.6786	0.9286	0.8929	0.8929	0.6786	1	1

,

Table 3. ACC and NMI of different multisource fusion methods using dataset 2.

	PCA	LLE	LE	MPCA	HTD	GTDA	TLPP	TDLA	CFM-HTD
NMI	0.2159	0.1423	0.0797	0.2556	0.3234	0.2063	0.1715	0.1598	0.3403
ACC	0.7288	0.5876	0.4832	0.7232	0.7655	0.6384	0.4520	0.4746	0.7797

and

Table 4. ACC and NMI of different multisource fusion methods using dataset 3.

	PCA	LLE	LE	MPCA	HTD	GTDA	TLPP	TDLA	CFM-HTD
NMI	0.2496	0.1992	0.2166	0.2199	0.3365	0.2762	0.2596	0.3885	0.4052
ACC	0.7742	0.6452	0.6774	0.8065	0.8338	0.7419	0.7419	0.8710	0.8710

.

In general, it was found that all the methods obtain better results for dataset 1 than for dataset 2 because optical images in dataset 1 present more obvious object structure and geometry characteristic that is easy to be identified than SAR images in dataset 2. In addition, it was also found that the results of different methods using dataset 1 are better that using dataset 3 because the ship slices in dataset 3 contain more background interferences than airplane slices in dataset 1. Moreover, it is seen that PCA obtains the best results among vector-based comparison methods. The reason is that PCA, as the conventional feature extraction method, can maintain the maximum energy of objects to obtain effective results. Moreover, it is also seen that TDLA, HTD, and TDLA obtain the best results among tensor-based comparison methods for datasets 1, 2, and 3, respectively. Remarkably, it is worth noting that CFM-HTD obtains the best results among all the methods for the two datasets. This is because CFM-HTD can extract coupled information contained in heterogeneous multisource data, and its inherent classification mechanism ensures the effectiveness of cluster and classification.

Subsequently, the experiments were further conducted to compare the performance of CFM-HTD with tensor-based comparison methods under different dimensions of extracted features, as shown in Figure 11.

The horizontal coordinate j denotes the dimension of extracted features $I_m^{\text{'}}=ceil\left(\frac{I_m}{j}\right)$. From these figures, it is observed that ACC and NMI will vary as the change in dimensions of extracted features. For dataset 1 and dataset 2, the performance of the TLPP method is weaker than other methods, and the TDLA and HTD methods can achieve the second-best results in dataset 1 and dataset 2, respectively. It is observed that the proposed CFM-HTD outperforms all comparison methods under different dimensions of extracted features, which further implies the effectiveness of the proposed CFM-HTD method for feature extraction using paired multisource data.

3.6. Evaluation of the Performance of CCT-HTD Compared with Typical Domain Adaptation Methods

To evaluate the effectiveness of the proposed CCT-HTD for domain adaptation, two datasets were applied to compare the classification accuracy of CCT-HTD with typical domain adaptation-oriented feature extraction methods, including PCA, HTD, TCA, CORAL, JDA, ATL, CMMS [41], and JFSSS-HFT [42]. For three datasets, source domain samples and target domain samples are denoted as S and T, respectively. In addition, two domain adaptation tasks were built, i.e., $S\to T$ and $T\to S$, where $S\to T$ denotes samples from the source domain and target domain are regarded as training set and test set, respectively. Since dataset 3 contain optical and SAR slices that present large characteristic difference, we used the same features tensors (i.e., morphology features) to describe both the optical and SAR slices to reduce the distribution discrepancy. Except for the JFSSS-HFT and CMMS methods, all the comparison methods can only handle homogeneous data. To meet their input requirements, the bilinear interpolation technique was used to adjust the image slices in source domain to the same sizes as the image slices in target domain. In addition, since the comparison methods can only handle input represented as a vector, the constructed feature tensors are vectorized to meet their input requirements. For dataset 1, due to the high dimensionality of the extracted features tensors, the vectorization results in CORAL, ATL, CMMS, and JFSSS-HFT exceeding the storage limitation of the computer. Therefore, CORAL, ATL, CMMS, and JFSSS-HFT were performed combined with PCA methods to reduce the storage requirement. To ensure a fair comparison, the grid-search method was utilized to obtain the best results for all the methods. For TCA, JDA, and CMMS, we chose either a linear kernel or a Gaussian kernel. For all comparison methods, the optimal dimensional parameters were $\left\{10,20,\dots ,100\right\}$. For TCA, ATL, CMMS, and JFSSS-HFT, the optimal regularization parameters were $\left\{0.1,0.2,\dots ,2\right\}$. For JFSSS-HFT, optimal $w_s$ and $w_t$ were $\left\{0.05,0.1,0.2,0.3\right\}$. The PCA method, TCA method, CORAL method, and JDA method are unsupervised feature transfer methods and do not require sample labels. The ATL method, CMMS method, and JFSSS-HFT method, are supervised methods and they need labeled samples. For HTD and the proposed CCT-HTD, the optimal dimensional parameters were from $I_m^{\text{'}}=ceil\left(\frac{I_m}{j}\right),j\in \left\{2,3,\dots ,8\right\}$. In addition, since the proposed CCT-HTD is a semi-supervised feature transfer method, half labeled samples and half unlabeled samples were used together in the experiments. The obtained classification results using 1NN and support vector machine (SVM) [43] across domains are shown in

Table 5. Classification accuracies of different domain adaptation methods with 1NN and SVM using dataset 1.

Classifier	Task	PCA	HTD	TCA	CORAL	JDA	ATL	CMMS	JFSSS-HFT	CCT-HTD
1NN	$S\to T$	47.2%	52.78%	77.8%	50%	63.89%	52.78%	52.78%	83.3%	86.1%
	$T\to S$	47.7%	53.85%	49.3%	47.7%	49.2%	46.2%	52.3%	83.1%	84.62
SVM	$S\to T$	58.33%	50%	80.56%	55.56%	69.44%	55.56%	55.56%	86.1%	86.1%
	$T\to S$	49.3%	50.77%	67.7%	46.2%	55.4%	49.2%	49.2%	78.5%	83.08%

,

Table 6. Classification accuracies of different domain adaptation methods with 1NN and SVM using dataset 2.

Classifier	Task	PCA	HTD	TCA	CORAL	JDA	ATL	CMMS	JFSSS-HFT	CCT-HTD
1NN	$S\to T$	59.89%	49.15%	61.58%	58.19%	68.93%	59.89%	72.88%	66.67%	73.45%
	$T\to S$	59.89%	51.41%	59.32%	20.90%	59.32%	40.68%	68.30%	61.02%	71.19%
SVM	$S\to T$	52.54%	51.41%	62.15%	24.29%	55.37%	48.02%	80.79%	51.89%	81.92%
	$T\to S$	44.63%	48.59%	51.97%	16.38%	52.54%	42.94%	78.53%	51.97%	80.79%

and

Table 7. Classification accuracies of different domain adaptation methods with 1NN and SVM using dataset 3.

Classifier	Task	PCA	HTD	TCA	CORAL	JDA	ATL	CMMS	JFSSS-HFT	CCT-HTD
1NN	$S\to T$	38.71%	35.48%	41.94%	48.39%	32.26%	48.39%	54.84%	58.06%	61.29%
	$T\to S$	45.16%	41.94%	54.84%	32.26%	54.84%	51.61%	58.06%	51.61%	61.29%
SVM	$S\to T$	48.39%	48.39%	41.94%	29.03%	48.39%	48.39%	58.06%	61.29%	64.62%
	$T\to S$	54.84%	48.39%	54.84%	25.81%	51.61%	51.61%	51.61%	58.06%	67.74%

.

From the above tables, it can be found that the classification accuracy of dataset 1 and dataset 2 is higher than that of dataset 3 in general because the optical images and SAR images share limited information leading to difficulties in obtaining better domain adaptation results. Since the PCA and HTD do not belong to domain adaptation technologies, it is observed that the direct application of PCA and HTD methods produces poor classification accuracy for both datasets due to the large distribution discrepancy between source and target domains. After applying domain adaptation methods, the classification accuracy is changed to various results. Specifically, the CORAL method obtains poor results for different domain adaptation tasks because it only considers the second-order statistical alignment of the samples without considering the category information of the samples. For the CMMS as well as the JFSSS-HFT method, their classification accuracies are higher than the other comparison methods due to their ability to utilize the labeling information of the samples as supervised methods. For dataset 1 and dataset 3, JFSSS-HFT obtains the best results among the comparison methods because it is a heterogeneous features extraction method that avoids the interpolation of images and jointly considers the sample weighting of the sample space and the feature transformation of the feature space to ensure the validity of the transferring results. For dataset 2, the CMMS method has the best performance among the comparison methods. It is worth noting that the proposed CCT-HTD achieves the best classification results across domains for the two datasets because CCT-HTD is the unique domain adaptation method that can handle heterogeneous feature tensors. Not only that, CCT-HTD can excavate class information and be robust to the outliers, thus ensuring better classification results. It indicates that the proposed CCT-HTD outperforms typical domain adaptation methods for feature extraction of heterogeneous remote sensing data from different sources.

To further validate the robustness of CCT-HTD, dataset 1 and dataset 2 were added with interference samples respectively to further examine the domain adaptation results. Specifically, seven slices of other types of aircraft were added to the source domain of dataset 1, and nine slices of other types of tanks or trucks were added to the source domain of dataset 2. Some of the interference samples are shown in Figure 12. By transferring the source domain mixed with interference samples to the target domain, the obtained experimental results are shown in

Table 8. Classification accuracies of different domain adaptation methods by adding interference samples with 1NN and SVM using dataset 1.

Classifier	Task	PCA	HTD	TCA	CORAL	JDA	ATL	CMMS	JFSSS-HFT	CCT-HTD
1NN	$S\to T$	30.56%	47.22%	77.8%	44.4%	50%	50%	47.22%	66.67%	83.3%
	$T\to S$	47.7%	47.69%	33.85%	47.7%	44.62%	69.27%	64.62%	76.92%	84.62
SVM	$S\to T$	41.67%	50%	80.56%	41.67%	55.56%	55.56%	52.78%	72.2%	83.3%
	$T\to S$	49.3%	46.15%	67.7%	46.2%	55.4%	52.3%	52.31%	78.5%	83.08%

and

Table 9. Classification accuracies of different domain adaptation methods by adding interference samples with 1NN and SVM using dataset 2.

Classifier	Task	PCA	HTD	TCA	CORAL	JDA	ATL	CMMS	JFSSS-HFT	CCT-HTD
1NN	$S\to T$	39.25%	45.76%	59.02%	56.83%	56.83%	48.63%	65.57%	49.18%	73.45%
	$T\to S$	24.19%	45.20%	56.99%	19.35%	63.98%	27.96%	69.35%	57.53%	70.43%
SVM	$S\to T$	30.11%	46.89%	49.46%	20.90%	50.82%	44.26%	78.53%	38.79%	80.79%
	$T\to S$	25.27%	45.76%	58.60%	15.59%	52.35%	24.19%	67.74%	46.77%	79.66%

.

Comparing the results with the addition of interference samples, it is found that the results of comparison methods change significantly after adding interference samples; most of them become worse. This is because the interference samples change the distribution of the source domain data and thus affect the cross-domain classification results. In contrast, since the CCT-HTD can utilize the adaptive sample-weighing matrix to remove outliers, the CCT-HTD can obtain similar results whether the dataset is mixed with interference samples or not. This further indicates that our CCT-HTD outperforms the typical domain adaptation-oriented feature extraction methods for object classification across sources.

4. Discussion

4.1. Discussion of the Experimental Results of the Proposed Methods

From the experimental results, it is seen that the proposed CFM-HTD and CCT-HTD can obtain high recognition accuracy for multisource fusion and domain adaptation using optical multiangle images and multiangle SAR images. However, it is worth noting that the accuracy of CCT-HTD using dataset 3 is not high. The reason is probably that the optical images and SAR images share limited information, causing a difficult domain adaptation. Nevertheless, the accuracy of CCT-HTD using dataset 3 is higher than the comparison methods. Consequently, it implies the proposed CFM-HTD and CCT-HTD outperform the typical multisource fusion-oriented and domain adaptation-oriented methods for different datasets, respectively.

4.2. Discussion of the Relationship between Coupled Heterogeneous Tucker Decomposition and the Existing Methods

To express the relationship between two types of C-HTD clearly, CFM-HTD and CCT-HTD are simplified as follows by ignoring the adaptive sample-weighing matrix.

$$\begin{array}{l}\underset{{𝒢}_1,{𝒢}_2,{\mathit{U}}_l^1,{\mathit{U}}_l^2,{\mathit{U}}_{L+1}}{\min }{‖{\chi }_1-{𝒢}_1{\times }_1{\mathit{U}}_1^1{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2+{‖{\chi }_2-{𝒢}_2{\times }_1{\mathit{U}}_1^2{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}‖}_F^2-\\ c\times \left({\displaystyle \sum _m{‖{𝒢}_1^m-\frac{1}{M}{𝒢}_1{\times }_{L+1}{\mathit{e}}_M‖}_F^2}+{\displaystyle \sum _m{‖{𝒢}_2^m-\frac{1}{M}{𝒢}_2{\times }_{L+1}{\mathit{e}}_M‖}_F^2}\right)\end{array}$$

(40)

$$\begin{array}{l}\underset{𝒢,{\mathit{U}}_l^s,{\mathit{U}}_l^t}{\min }{‖{\chi }_s-𝒢{\times }_1{\mathit{U}}_1^s{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^s‖}_F^2+{‖{\chi }_t-𝒢{\times }_1{\mathit{U}}_1^t{\times }_2\dots {\times }_{L+1}{\mathit{U}}_{L+1}^t‖}_F^2-\\ c\times \left({\displaystyle \sum _m{‖{𝒢}^m-\frac{1}{M}𝒢{\times }_{L+1}{\mathit{e}}_M‖}_F^2}\right).\end{array}$$

(41)

It is observed that the CFM-HTD and CCT-HTD have a symmetric structure. For CFM-HTD, it requires that the category indicator factor matrix corresponding to different sources is identical. For CCT-HTD, it requires that the core tensor corresponding to different sources is identical.

In addition, when the input is the single-source data, the current C-HTD is degraded to HTD. When the input is the single-source data without the constraints of ${\mathit{U}}_{L+1}$, the C-HTD is degraded to standard TD. Furthermore, when the input is the single-source data, and its representation is a vector, then the C-HTD is degraded to the constrained matrix decomposition used for the cluster [44].

4.3. Discussion of the Convergence and Complexity

For the two types of C-HTD, it is found that the optimization problem is the unconstrained quadratic programming with respect to core tensor. To ensure the convexity of quadratic programming, the second-order derivative of the objective function with respect to the core tensor should be positive, i.e., $\widehat{\mathit{U}}\left(i,i\right)+\mathit{L}\left(i,i\right)>0$ for each i (see Equations (29) and (59)). Therefore, the regularization parameter c should not be overly large. When the regularization parameter c is suitable, the optimal core tensor can be expressed as the analytical expression of the other variables. In addition, since the feasible region of the optimization problem of coupled heterogeneous Tucker decompositions is bounded, the value of the objective function is bounded. Applying the proposed alternative optimization scheme will generate the monotonically non-increasing sequence. Therefore, there exists a limit, and the iteration updating may converge to the optimal solution.

To evaluate the computational complexity of the proposed CFM-HTD and CCT-HTD conveniently, let ${\epsilon }_s=0$ and assume the dimensions of used samples ${ℝ}^{I_1,I_2,\dots ,I_L}$ and the optimal core tensors ${ℝ}^{i_1,i_2,\dots ,i_L}$ (set $i_1=i_2=\dots =i_{L+1}$, $I_1=I_2=\dots =I_{L+1}$) are the same for both the CFM-HTD and CCT-HTD. In this way, both the CFM-HTD and CCT-HTD consist of three main optimization solving parts, i.e., (1) optimize the orthonormal factor matrix; (2) optimize the class-indicator factor matrix; (3) optimize the core tensor, and thus present the similar computational complexity. For convenience, we used CFM-HTD as an example to analyze the computational complexity.

When optimizing the orthonormal factor matrix, it is needed to calculate ${\mathit{G}}_1^{\left(l\right)}{\mathit{H}}_1^{\left(l\right)T}{\mathit{X}}_1^{\left(l\right)T}$. Since ${\mathit{G}}_1^{\left(l\right)}{\mathit{H}}_1^{\left(l\right)T}=Ma{t}_{\left(l\right)}\left({𝒢}_1{\displaystyle \prod _{j\ne l}{\times }_j{\mathit{U}}_j^1}\right)$, the main computational complexity produced by multiplications is $O\left({\displaystyle \sum _{k\ne l}{\left(i_k\right)}^2{I}_k{\displaystyle \prod _{j\ne k}{i}_j}}+i_l{I}_l{\displaystyle \prod _{j\ne l}{\left(I_j\right)}^2}\right)$. When optimizing the class-indicator factor matrix, the time consumption is produced by calculating Equation (21), i.e., the multiplications in ${\mathit{G}}_1^{\left(L+1\right)}{\mathit{G}}_1^{\left(L+1\right)T}$, ${\mathit{G}}_2^{\left(L+1\right)}{\mathit{G}}_2^{\left(L+1\right)T}$, ${\mathit{G}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)T}{\mathit{X}}_1^{n\left(L+1\right)T}$, and ${\mathit{G}}_2^{\left(L+1\right)}{\mathit{H}}_2^{\left(L+1\right)T}{\mathit{X}}_2^{n\left(L+1\right)T}$, the corresponding computational complexity is $O\left(2{\left(i_{L+1}\right)}^2{\displaystyle \prod _{j\ne L+1}{\left(i_j\right)}^2}+2{\displaystyle \sum _{k\ne L+1}{\left(i_k\right)}^2{I}_k{\displaystyle \prod _{j\ne k}{i}_j}}+2i_{L+1}\times I_{L+1}{\displaystyle \prod _{j\ne L+1}{\left(I_j\right)}^2}\right)$. When optimizing the core tensor, the time consumption is produced by the multiplications ${\mathit{U}}_{L+1}{\left(:,i\right)}^T{\mathit{X}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)}$ in Equation (29). Since ${\mathit{X}}_1^{\left(L+1\right)}{\mathit{H}}_1^{\left(L+1\right)}=Ma{t}_{\left(L+1\right)}\left({\chi }_1{\displaystyle \prod _{j\ne L+1}{\times }_j{\mathit{U}}_j^{1T}}\right)$, the main computational complexity is $O\left({\displaystyle \sum _{k\ne L+1}{\left(I_k\right)}^2{i}_k{\displaystyle \prod _{j\ne k}{I}_j}}+I_{L+1}{\displaystyle \prod _{j\ne L+1}{i}_j}\right)$. Therefore, for each iteration of the proposed method, the total computational complexity is nearly:

$$O(3{\displaystyle \sum _{k\ne l}{\left(i_k\right)}^2{I}_k{\displaystyle \prod _{j\ne k}{i}_j}}+3i_l{I}_l{\displaystyle \prod _{j\ne l}{\left(I_j\right)}^2}+2{\left(i_{L+1}\right)}^2{\displaystyle \prod _{j\ne L+1}{\left(i_j\right)}^2}+{\displaystyle \sum _{k\ne L+1}{\left(I_k\right)}^2{i}_k{\displaystyle \prod _{j\ne k}{I}_j}}+I_{L+1}{\displaystyle \prod _{j\ne L+1}{i}_j}).$$

(42)

5. Conclusions

To extract useful information from heterogeneous multisource remote sensing data, the coupled heterogeneous Tucker decomposition method as a unified framework is proposed for multisource fusion-oriented and domain adaptation-oriented feature extraction. It consists of two versions of sub-methods according to different coupled constraints, i.e., CFM-HTD and CCT-HTD, where the former is used to extract complementary features for multisource fusion and the latter is used to mine shared features for domain adaptation. Compared with typical TD, HTD, as well as the other multisource fusion-oriented and domain adaptation-oriented feature extraction methods that can only handle vector or homogeneous tensors as input, the CFM-HTD and CCT-HTD can accept heterogeneous tensors as input to excavate complementary or shared information from multisource remote sensing data in an associative manner. In addition, the CFM-HTD and CCT-HTD can adapt to supervised and semi-supervised situations using the class-indicator factor matrix. Moreover, in contrast to the existing domain adaptation-oriented feature extraction methods that are susceptible to outliers, the CCT-HTD can remove outliers using the adaptive sample-weighing matrix to reduce the occurrence of negative transfer.

The future work focuses on extending coupled heterogeneous Tucker decomposition to cope with remote sensing image change detection and developing the coupled heterogeneous CP decomposition method.