Object Tracking and Geo-Localization from Street Images
Abstract
:1. Introduction
- An enhanced version of the ARTS [9] dataset, ARTSv2, to serve as a benchmark for the field of object geo-localization.
- A novel object geo-localization technique that handles a large number of classes and objects existing in an arbitrary number of frames using only accessible hardware.
- An object tracking system to collapse a set of detections in a noisy, low-frame rate environment into final geo-localized object predictions.
2. Related Work
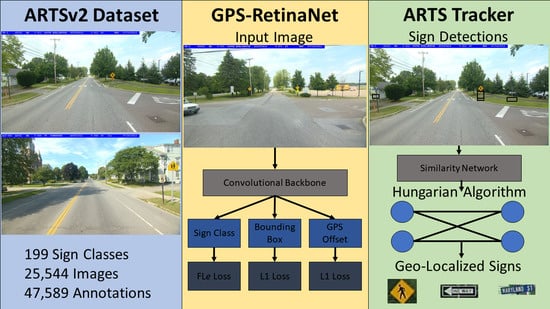
3. Datasets
3.1. Existing Datasets
3.2. ARTSv2 Dataset
3.3. Dataset Construction
3.4. Unique Characteristics
4. Materials and Methods
4.1. System Overview
4.2. GPS RetinaNet
4.3. Multi-Object Tracker
4.3.1. Similarity Network
4.3.2. Modified Hungarian Algorithm
4.3.3. Geo-Localized Sign Prediction
5. Results
5.1. Object Detector Performance
5.2. Object Detector GPS Prediction
5.3. Similarity Network
5.4. Tracker
5.5. Comparison to Other Methods
6. Discussion
6.1. Object Detector Performance
6.2. Object Detector GPS Performance
6.3. Similarity Network
6.4. Tracker
6.5. Comparison to Other Methods
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
| Tracker Performance Comparisons | |||
|---|---|---|---|
| Tracker | True Positives | False Negatives | False Positives |
| Boosting [36] | 8062 | 173 | 24,425 |
| MIL [37] | 8068 | 167 | 24,130 |
| KCF [38] | 8061 | 175 | 25,812 |
| TLD [39] | 8055 | 180 | 21,903 |
| MedianFlow [40] | 8054 | 181 | 20,834 |
| GoTurn [41] | 8049 | 186 | 22,203 |
| MOSSE [42] | 8042 | 193 | 21,422 |
| CSRT [43] | 8061 | 174 | 23,052 |
| Proposed Tracker | 6677 | 2759 | 1558 |
References
- Chaabane, M.; Gueguen, L.; Trabelsi, A.; Beveridge, R.; O’Hara, S. End-to-End Learning Improves Static Object Geo-Localization From Video. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Virtual, 5–9 January 2021; pp. 2063–2072. [Google Scholar]
- Nassar, A.S.; Lefèvre, S.; Wegner, J.D. Simultaneous multi-view instance detection with learned geometric soft-constraints. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6559–6568. [Google Scholar]
- Nassar, A.S.; D’Aronco, S.; Lefèvre, S.; Wegner, J.D. GeoGraph: Graph-Based Multi-view Object Detection with Geometric Cues End-to-End. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 488–504. [Google Scholar]
- McManus, C.; Churchill, W.; Maddern, W.; Stewart, A.D.; Newman, P. Shady dealings: Robust, long-term visual localisation using illumination invariance. In Proceedings of the Institute of Electrical and Electronics Engineers (IEEE) International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 901–906. [Google Scholar] [CrossRef]
- Suenderhauf, N.; Shirazi, S.; Jacobson, A.; Dayoub, F.; Pepperell, E.; Upcroft, B.; Milford, M. Place recognition with ConvNet landmarks: Viewpoint-robust, condition-robust, training-free. In Proceedings of the Robotics: Science and Systems XI, Rome, Italy, 13–17 July 2015; pp. 1–10. [Google Scholar]
- Krylov, V.A.; Kenny, E.; Dahyot, R. Automatic Discovery and Geotagging of Objects from Street View Imagery. Remote Sens. 2018, 10, 661. [Google Scholar] [CrossRef] [Green Version]
- Krylov, V.A.; Dahyot, R. Object geolocation using mrf based multi-sensor fusion. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 2745–2749. [Google Scholar]
- Wilson, D.; Zhang, X.; Sultani, W.; Wshah, S. Visual and Object Geo-localization: A Comprehensive Survey. arXiv 2021, arXiv:2112.15202. [Google Scholar]
- Almutairy, F.; Alshaabi, T.; Nelson, J.; Wshah, S. ARTS: Automotive Repository of Traffic Signs for the United States. IEEE Trans. Intell. Transp. Syst. 2019, 22, 457–465. [Google Scholar] [CrossRef]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; pp. 307–312. [Google Scholar]
- Fairfield, N.; Urmson, C. Traffic light mapping and detection. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5421–5426. [Google Scholar]
- Soheilian, B.; Paparoditis, N.; Vallet, B. Detection and 3D reconstruction of traffic signs from multiple view color images. ISPRS J. Photogramm. Remote Sens. 2013, 77, 1–20. [Google Scholar] [CrossRef]
- Hebbalaguppe, R.; Garg, G.; Hassan, E.; Ghosh, H.; Verma, A. Telecom Inventory management via object recognition and localisation on Google Street View Images. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 725–733. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 21–23 September 2005; Volume 1, pp. 886–893. [Google Scholar]
- Liu, C.J.; Ulicny, M.; Manzke, M.; Dahyot, R. Context Aware Object Geotagging. arXiv 2021, arXiv:2108.06302. [Google Scholar]
- Lin, T.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar] [CrossRef] [Green Version]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast R-CNN Object detection with Caffe. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.B.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. arXiv 2018, arXiv:1708.02002. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Zhu, J.; Yang, H.; Liu, N.; Kim, M.; Zhang, W.; Yang, M.H. Online multi-object tracking with dual matching attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 366–382. [Google Scholar]
- Voigtlaender, P.; Krause, M.; Osep, A.; Luiten, J.; Sekar, B.B.G.; Geiger, A.; Leibe, B. Mots: Multi-object tracking and segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7942–7951. [Google Scholar]
- Son, J.; Baek, M.; Cho, M.; Han, B. Multi-object tracking with quadruplet convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5620–5629. [Google Scholar]
- Xu, J.; Cao, Y.; Zhang, Z.; Hu, H. Spatial-temporal relation networks for multi-object tracking. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 3988–3998. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H.S. Fully-Convolutional Siamese Networks for Object Tracking. In Proceedings of the Computer Vision—ECCV 2016 Workshops, Amsterdam, The Netherlands, 11–14 October 2016; Hua, G., Jégou, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 850–865. [Google Scholar]
- Xiang, Y.; Alahi, A.; Savarese, S. Learning to Track: Online Multi-object Tracking by Decision Making. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4705–4713. [Google Scholar] [CrossRef] [Green Version]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 11621–11631. [Google Scholar]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef] [Green Version]
- Tzutalin. Tzutalin. LabelImg. Git Code. 2015. Available online: https://github.com/tzutalin/labelImg (accessed on 5 April 2022).
- Kuhn, H.W. The Hungarian Method For The Assignment Problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Lin, T.; Maire, M.; Belongie, S.J.; Bourdev, L.D.; Girshick, R.B.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. arXiv 2014, arXiv:1405.0312. [Google Scholar]
- Grabner, H.; Grabner, M.; Bischof, H. Real-Time Tracking via On-line Boosting. In Proceedings of the British Machine Vision Conference 2006, Edinburgh, UK, 4–7 September 2006; Volume 1, pp. 47–56. [Google Scholar] [CrossRef] [Green Version]
- Babenko, B.; Yang, M.H.; Belongie, S. Visual tracking with online Multiple Instance Learning. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 983–990. [Google Scholar] [CrossRef]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [Green Version]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-Learning-Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409–1422. [Google Scholar] [CrossRef] [Green Version]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Forward-Backward Error: Automatic Detection of Tracking Failures. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2756–2759. [Google Scholar] [CrossRef] [Green Version]
- Held, D.; Thrun, S.; Savarese, S. Learning to Track at 100 FPS with Deep Regression Networks. arXiv 2016, arXiv:1604.01802. [Google Scholar]
- Bolme, D.; Beveridge, J.; Draper, B.; Lui, Y. Visual object tracking using adaptive correlation filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar] [CrossRef]
- Lukežič, A.; Vojíř, T.; Čehovin Zajc, L.; Matas, J.; Kristan, M. Discriminative Correlation Filter with Channel and Spatial Reliability. Int. J. Comput. Vis. 2018, 126, 671–688. [Google Scholar] [CrossRef] [Green Version]











| Pasadena Multi-View ReID [2] | Traffic Light Geo-Localization (TLG) [1] | ARTS v1.0 [9] | ARTSv2.0 | ||
|---|---|---|---|---|---|
| Easy | Challenging | ||||
| Number of classes | 1 | 1 | 78 | 171 | 199 |
| Number of images | 6141 | 96,960 | 9647 | 19,908 | 25,544 |
| Number of annotations | 25,061 | Unknown | 16,540 | 35,970 | 47,589 |
| Side of the road | 🗸 | ||||
| Assembly | 🗸 | ||||
| Unique Object IDs | 🗸 | 🗸 | 🗸 | ||
| 5D Poses | 🗸 | ||||
| GPS | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| Color Channels | RGB | RGB | RGB | RGB | RGB |
| Image Resolution | |||||
| Publicly Available | 🗸 | 🗸 | 🗸 | 🗸 | |
| Loss Function | mAP50 | APmin | AP50% | APmax |
|---|---|---|---|---|
| RetinaNet-50 (FL) | 69.9 | 15.9 | 70.0 | 100 |
| RetinaNet-50 (FLe) | 70.1 | 17.2 | 70.1 | 100 |
| Percentile | Absolute Error |
|---|---|
| 50 | 0.0165 |
| 75 | 0.1195 |
| 90 | 0.3846 |
| 95 | 0.6106 |
| 97 | 0.7436 |
| 98 | 0.8064 |
| 99 | 0.8844 |
| End-to-End Performance | ||||
|---|---|---|---|---|
| Year Collected | 2012 | 2013 | 2014 | All |
| Noteworthy Features | Towns | Highways | Rural Segments and Small Towns | All Geographical Environments |
| True Positives | 264 | 3170 | 3179 | 6163 |
| False Negatives | 176 | 604 | 842 | 1622 |
| False Positives | 67 | 826 | 1581 | 2474 |
| Geo-Localization Performance Comparisons | |||||
|---|---|---|---|---|---|
| Tracking Method | True Positives | False Negatives | False Positives | Mean GPS Error | STD GPS Error |
| Triangularization | 6079 | 3000 | 1918 | 6.67 | 4.33 |
| MRF | 6677 | 4379 | 2156 | 6.57 | 4.98 |
| Frame of Interest | 6677 | 2759 | 1558 | 5.85 | 4.40 |
| Weighted Average | 6670 | 2751 | 1565 | 5.81 | 4.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, D.; Alshaabi, T.; Van Oort, C.; Zhang, X.; Nelson, J.; Wshah, S. Object Tracking and Geo-Localization from Street Images. Remote Sens. 2022, 14, 2575. https://doi.org/10.3390/rs14112575
Wilson D, Alshaabi T, Van Oort C, Zhang X, Nelson J, Wshah S. Object Tracking and Geo-Localization from Street Images. Remote Sensing. 2022; 14(11):2575. https://doi.org/10.3390/rs14112575
Chicago/Turabian StyleWilson, Daniel, Thayer Alshaabi, Colin Van Oort, Xiaohan Zhang, Jonathan Nelson, and Safwan Wshah. 2022. "Object Tracking and Geo-Localization from Street Images" Remote Sensing 14, no. 11: 2575. https://doi.org/10.3390/rs14112575
APA StyleWilson, D., Alshaabi, T., Van Oort, C., Zhang, X., Nelson, J., & Wshah, S. (2022). Object Tracking and Geo-Localization from Street Images. Remote Sensing, 14(11), 2575. https://doi.org/10.3390/rs14112575