Registration of Multisensor Images through a Conditional Generative Adversarial Network and a Correlation-Type Similarity Measure

Abstract

The automatic registration of multisensor remote sensing images is a highly challenging task due to the inherently different physical, statistical, and textural characteristics of the input data. Information-theoretic measures are often used to favor comparing local intensity distributions in the images. In this paper, a novel method based on the combination of a deep learning architecture and a correlation-type area-based functional is proposed for the registration of a multisensor pair of images, including an optical image and a synthetic aperture radar (SAR) image. The method makes use of a conditional generative adversarial network (cGAN) in order to address image-to-image translation across the optical and SAR data sources. Then, once the optical and SAR data are brought to a common domain, an area-based ${\ell }^2$ similarity measure is used together with the COBYLA constrained maximization algorithm for registration purposes. While correlation-type functionals are usually ineffective in the application to multisensor registration, exploiting the image-to-image translation capabilities of cGAN architectures allows moving the complexity of the comparison to the domain adaptation step, thus enabling the use of a simple ${\ell }^2$ similarity measure, favoring high computational efficiency, and opening the possibility to process a large amount of data at runtime. Experiments with multispectral and panchromatic optical data combined with SAR images suggest the effectiveness of this strategy and the capability of the proposed method to achieve more accurate registration as compared to state-of-the-art approaches.

1. Introduction

Thanks to the increasing number of Earth observation missions, there is a constantly growing availability of multisource satellite imagery. Several types of satellites, equipped with a variety of active and passive instruments, produce data with different spatial resolutions, frequencies, polarizations, etc. Therefore, in many applications, several acquisitions are usually available over the same area. However, in order to jointly exploit such acquisitions, it is usually necessary to make the related images spatially aligned. In general terms, the process of aligning different sets of image data and of referencing them into a common coordinate system is named image registration [1]. Input data for registration may be multiple photographs, data from different sensors, times, or viewpoints [2]. Normally, one image is fixed and taken as the “reference image” (or “master image”), while all the other images, named “input images” (or “slave images”), are registered to the reference image by finding the geometrical transformation that maximizes their matching, e.g., considering a given similarity measure [1]. Besides remote sensing, image registration is of paramount importance in the fields of computer vision, medical imaging, military automatic target recognition, etc. [3]. Indeed, the registration process is necessary in order to be able to compare or integrate spatial data corresponding to the same scene but obtained from different measurements.

The consolidated approaches to multisensor image registration usually involve semi-interactive procedures based on manually annotated control points. However, with the registration demand that proportionally increases with the availability of data, manual approaches are showing their limits, and they are becoming less and less feasible. Therefore, increasing attention is currently moving toward automatic methods that do not require (or, at least, minimize) human interaction, with a special focus on their scalability to the amount of input data.

In recent years, image-to-image translation methods based on deep learning have attracted considerable attention when applied to multisensor image registration tasks [4,5]. These methods are inspired by neural style transfer and aim to transform one or both images to project them onto a common domain. As a consequence, it is easier to compare their inherently different characteristics and get features useful for their registration. In particular, approaches based on generative adversarial networks (GANs), combined with feature-based marked-point extraction, proved to be efficient [6]. A GAN is composed of two neural networks trained in competition [7]. In particular, a conditional GAN (cGAN) is aimed at generating output data whose distribution matches that of a target source [7] from a non-noise input source [8].

In particular, state-of-the-art methods integrating cGANs within image registration tasks generally follow a feature-based strategy [6,9]. We recall that feature-based registration methods extract spatial features (e.g., point, linear, or curvilinear features) from the image pair to be registered and use them for achieving a spatial match [1]. After a cGAN is used to bring one image into the domain of the other, a feature-based image registration method based on the extraction and matching of points is applied [6,9].

Conversely, the method proposed here combines the use of cGAN with area-based image registration, i.e., with an approach to spatial matching that operates on the whole image area. Area-based registration is known to be more accurate and robust than feature-based solutions, at the cost of being computationally heavier, especially when information-theoretic functionals are used for matching purposes [1]. This paper adopts the area-based strategy while keeping the computational complexity to a low level at runtime. This is accomplished by moving most of the computational effort to the offline training of the cGAN and by using an ${\ell }^2$ similarity measure at runtime. In detail, the non-noise input source of the cGAN is an optical image, while the desired output consists of an image with SAR-like distribution. The obtained SAR-like image is then registered with the original SAR image using the transformation parameters obtained by optimizing the ${\ell }^2$ similarity measure via the nonlinear COBYLA algorithm [10].

The novel contribution of the proposed method consists in the development of a GAN-based image registration framework that allows the application of a fast and efficient ${\ell }^2$ similarity measure in a multisensor optical-SAR scenario. In fact, while the latter per se is usually not feasible in its direct application to multisensor imagery, its application is enabled by the domain adaptation stage performed through a cGAN, capable of handling the multisensor complexity in the offline phase and simplifying the online workload. In particular, as compared to the recent literature on multisensor optical-SAR image registration and on GAN-based models in multisource remote sensing, the proposed approach integrates a cGAN architecture with an area-based—and not feature-based—registration strategy, thus taking benefit of its capability to achieve low registration errors.

In order to experimentally validate the developed technique, three datasets with different characteristics are used: two of them consist of multispectral and SAR data at 10 m spatial resolutions, while the third consists of panchromatic and SAR imagery at 0.5 m resolution.

A preliminary version of this work was published by the authors in the conference paper [11], while a subset of the experimental results appeared in the conference paper [12]. The present article extends these works by providing a more in-depth methodological analysis and by expanding the experimental evaluation of the performances with the use of two additional datasets associated with different areas and/or sensors.

The paper is organized as follows. Section 1.1 reviews the previous related work on the registration of multisensor remote sensing images and recalls the building blocks of registration methods and image-to-image translation based on deep learning. Section 2 presents the methodological formulation of the proposed approach, as well as the algorithm used to solve the corresponding optimization problem, together with the chosen transformation model and similarity measure. The datasets used for the experimental validation are also described. Experimental results and comparisons are then presented in Section 3, together with the description of the experimental setup. The results are discussed in Section 4. Finally, conclusions are drawn in Section 5.

1.1. Previous Work

The main components of an image registration method typically include the geometric transformation used to transform the input image (see Section 1.1.1), a functional comparing the reference and input images during the registration process (see Section 1.1.2), and the strategy used to find the transformation that optimizes such a functional (see Section 1.1.3).

1.1.1. Geometric Transformations

Suppose that the input image $u(x,y)$ is defined over a coordinate system $(x,y)$, while the reference image $v(X,Y)$ is defined over a coordinate system $(X,Y)$. The goal of image registration is to find the geometric transformation $T:(X,Y)\mapsto (x,y)$ that modifies the input image so that it is defined in the same coordinate system as the reference image, i.e., so that $u\left[T\right(X,Y\left)\right]$ spatially matches $v(X,Y)$ [1]. More precisely, this definition characterizes global image registration approaches, in which a consistent geometric transformation is assumed to exist across the whole scene associated with the input and reference images.

A rather general case is represented by the affine transformations. They are identified by six parameters, which include translation over the x-axis $T_x$ ($T_x\in \mathbb{R}$), translation over the y-axis $T_y$ ($T_y\in \mathbb{R}$), rotation angle $\theta$ ($0\le \theta \le 2\pi$), scale factor on the x-axis $k_x$ ($k_x>0$), scale factor on the y-axis $k_y$ ($k_y>0$), and shear angle $\varphi$ ($0\le \varphi \le \pi$) [13]:

$$\begin{array}{c}\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& -T_x\\ 0& 1& -T_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{k}_x& 0& 0\\ 0& k_y& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos\left(\theta \right)& -sin\left(\theta \right)& 0\\ sin(\theta +\varphi )& cos(\theta +\varphi )& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right].\end{array}$$

(1)

Particular cases of affine transformations are represented by rotation-scale-translation (RST) transformations (similarity transformations), where the shear angle is zero $(\varphi =0)$, and the scale factor is the same in the two dimensions $(k_x=k_y=k)$. Rigid transformations, in turn, are a special case of similarity transformations where there is no impact on the scale factor $(k=1)$. Shift transformations are rigid transformations characterized by a simple translation of the input image $(\theta =0)$ [14]. Other transformation models comprise polynomial and non-homogeneous models. Such transformations allow more flexibility at the cost of having a higher number of parameters to tune. Further details are provided in the comparative study reported in [15].

1.1.2. Similarity Measures

Once the family of transformations is selected, a matching strategy involving a suitable functional should be considered. The matching strategies may be divided into area-based, feature-based, and hybrid approaches.

(a)

Area-based methods operate with the entire image area, usually relying on similarity and information-theoretic measures [1,16]. On the one hand, area-based methods are computationally heavier than the feature-based strategies (see point b) because of the need to compute a functional by taking into consideration the whole image or generally large image regions. On the other hand, the accuracy achievable by such techniques is generally higher than that achieved by feature-based algorithms [1].

(b)

Feature-based methods operate on spatial features extracted from the input and reference images rather than on the whole image area. They are generally faster but often less accurate than area-based methods, and the accuracy of the registration result depends on the accuracy of the feature extraction method that is being used. There exist different strategies for the extraction of informative features. In particular, feature-point registration algorithms [1] extract a set of distinctive and highly informative individual points from both images and then find the geometric transformation that matches them. Feature points are named in different ways, including control points, tie-points, and landmarks. Well-known approaches in this area are those based on scale-invariant feature transforms (SIFT) [17], speeded-up robust features (SURF) [18], maximally stable extremal regions (MSER) [19], and Harris point detectors [20]. Other features of interest may be curvilinear and could be extracted by using edge detection algorithms [1], generalized Hough transforms [21], or stochastic geometry (e.g., marked point processes, MPPs) [22].

(c)

Hybrid methods are aimed at taking advantage of both the accuracy of area-based methods and the limited computational burden of feature-based methods. An example is provided by [23], where image registration is initialized using a SIFT-based strategy, and the resulting parameters are then refined via an area-based solution. Similarly, the methods in [24,25] are based on the extraction from planetary images of ellipsoidal features representing the craters using an MPP model. The result of such feature-based registration step is then further refined using an area-based strategy that makes use of the highly accurate mutual information similarity measure. Other kinds of hybrid registration methods are reported in [26], where global intensity measures are integrated with geometric configurational constraints, and [27], where SIFT and mutual information are combined in a coarse-to-fine strategy.

With regard to area-based registration, among the possible functionals, mutual information (MI), an information-theoretic functional that characterizes the relationship between the statistical distributions of the pixel intensities—rather than comparing couples of pixel intensities per se—, is often well suited for the multisensor scenario, where the images to be registered have different statistics and acquisition geometries [28,29,30]. The main drawback is that, while MI is more robust and less sensitive to noise than correlation-based measures, it requires estimating both the joint and the marginal distributions of the two input images, which can be a computationally heavy task, especially in the case of large-scale imagery. Bivariate histograms and Parzen window estimators [31] are well-known non-parametric approaches that have been frequently used in the computation of MI functionals. Another approach worth mentioning to evaluate MI is a non-parametric estimator based on the distances of each sample to its k-th nearest neighboring sample [32].

Similarity measures based on cross-correlation criteria [33,34] are computationally cheap (thanks to the possibility of calculating them through fast Fourier transforms) but often poorly suited for a direct application to multisensor data. Indeed, the relation between images collected by significantly different sensors in the same area is hardly captured through the simple cross-correlation between the intensity values.

1.1.3. Optimization Strategies

Once a proper matching functional has been defined, an algorithm capable of optimizing the similarity measure with respect to the transformation parameters is necessary. Generally speaking, the optimizers can be broadly divided into two categories: global and local methods. The methods belonging to the former category aim at finding a global optimum of a function. Among those, there are genetic algorithms (or, more generally, evolutionary algorithms) [35], in which a population of randomly generated candidate solutions is let evolve and is simulated to anneal [36], which progressively decrease and reincrease an energy function in order to ergodically converge to a global minimum. These techniques often require a long time to converge and are computationally intensive. Furthermore, convergence to a global optimum is often not guaranteed unless quite specific conditions are satisfied [36]. Local minimizers usually consider an initial solution and then try to find a better solution by exploring the search space guided by a local gradient (or an approximation thereof). They can end up being stuck in local minima but are generally faster at converging [37].

It is worth noting that the functionals used for registration purposes are sometimes non-differentiable functions of the transformation parameters, thus requiring methods that do not need to compute gradients, Hessians, or higher-order derivatives.

1.1.4. Multisensor Image Registration

The registration of multisensor images is a challenging problem that has been addressed in the literature of the past decades. Initially, the registration was mainly performed manually by extracting and matching ground control points. Then, the increased availability of multisensor data and the growing interest in large-area surveys [38] motivated the design and development of automatic registration methods. Due to the different nature of the input data and the resulting poor effectiveness of correlation-type metrics, in the 1990s, automatic registration methods were based on the extraction and matching of contour-based information. Some examples are shown in [39], where the use of region boundaries and other strong edges as matching primitives was proposed, and in [40], where an elastic contour matching method was developed. In the same period, wavelet transforms [38], and information-theoretic measures [41] were used to match heterogeneous data sources.

Subsequently, in the field of computer vision, feature-based single-sensor image registration methods, such as the SIFT [42], were developed and started to gain popularity. Such feature-based methods were also used in the remote sensing field, and, in particular, they have been adapted and evolved for the case of multisensor registration. Examples are the improved SIFT in [43] and the SAR-SIFT technique in [44]. Both methods introduce a new definition of the extracted features in such a way that their sensitivity to the different natures of optical and radar data is reduced. More recent examples following the same philosophy are the position, scale, and orientation SIFT (PSO-SIFT) method in [45] and the optical-to-SAR SIFT (OS-SIFT) technique in [46].

In the last decade, different solutions have been proposed, ranging from multi-step methods such as the one in [47], which combines area-based MI with local geometric matching, to techniques based on novel measures such as the structural similarity in [48]. Other examples are provided by the method in [49], which combines MI with wavelets and solves the related optimization problem via simulated annealing, and the method in [50], which uses an ant-colony optimization algorithm.

Recently, with the growing interest toward deep learning solutions, image-to-image translation concepts have started to become attractive for multisensor image registration. Indeed, image-to-image translation methods [8] have started flourishing in the last decade and have gained remarkable popularity in recent years in the field of computer vision. Roughly speaking, image-to-image translation refers to the set of methods that process an input image to output a new image, which has the same shape as the input, but whose semantics may be different from the original. Indeed, this type of processing proves useful in several applications such as image segmentation [51], colorization [52], and super-resolution [53]. The philosophy is inherited from neural style transfer [54], whose aim is to join the characteristics of two images. The first one is a content image, while the second one is a style image. Then, a neural network is trained in order to generate a third image that joins the two, repainting the content image with the style of the other image. The first attempts by the authors of [55] were used to discriminate layers between those closer to the input of the network, and the subsequent ones were used in relation to what such layers normally learn. On the one hand, the first layers of the network see smaller portions of the image and are usually related to low-level features, such as edges, corners, and curves. On the other hand, thanks to pooling, the last layers are sensitive to wider contexts. The general aim is to minimize a cost function that depends on certain layers for the content and other layers for the style. Furthermore, more recent approaches make use of architecture designs based on autoencoders [7] and adversarial networks [56] to define domain adaptation models. A cGAN transforms one image onto the domain of the other by combining two separate networks, named generator and discriminator, in a competitive manner. The generator aims to simulate output data consistent with the first domain from input data drawn from the second domain. The discriminator aims to detect whether its input is truly from the first domain or has been simulated by the generator.

GAN-type networks have recently been applied in several remote sensing image analysis tasks. Focusing first on optical data, examples are provided by the applications to hyperspectral image classification [57] and to pansharpening [58,59], where panchromatic and multispectral data are processed in order to produce a synthetic image characterized by high spatial and spectral information. Then, focusing on multisensor scenarios where optical and SAR data are used jointly, GAN-based image-to-image translation has been applied, for example, for cloud removal [60] and change detection [14,61]. In the latter case, images collected by a given sensor are translated into the domain of the other sensor using dedicated loss functions that focus the translation on the unchanged portion of the scene. In the cloud removal case, image-to-image translation is intended from the SAR domain to the optical one. Conversely, in the change detection case, the processing pipelines either combine both optical-to-SAR and SAR-to-optical translations or make use of an additional latent space into which the two sources are mapped.

Focusing on the multisensor image registration task, provided that the adaptation step is successful, single-sensor registration methods can be applied to the output of the network to address the registration problem. Examples are provided in [4,62]. Both such methods combine deep architectures for image-to-image translation only with feature-based registration schemes. In [12], an experimental comparison of deep cGAN-based registration and traditional approaches is presented. Furthermore, the method proposed in [63] uses Siamese networks and contrast learning [64] to learn a representation space and then applies a cross-correlation measure to detect horizontal alignments in the images. The latent space representation by means of Siamese networks is a viable domain adaptation option for registration purposes. However, the inherent geometric and radiometric differences between images in the SAR and optical domains might possibly limit the performance of such networks [65].

2. Materials and Methods

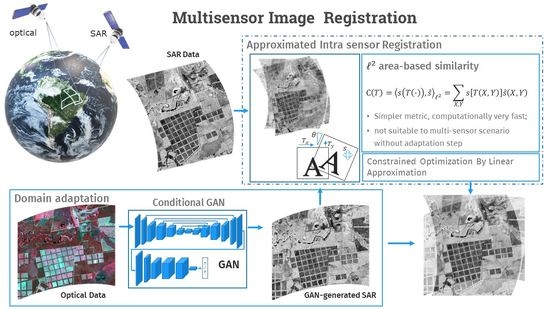
2.1. Assumptions and Overall Architecture of the Proposed Method

The key idea of the proposed method is that, leveraging on the domain adaptation capabilities of GAN architectures, the application of the aforementioned area-based techniques is favored because the optical and SAR data are brought together in a common domain in which they become more homogeneous and directly comparable. This process favors using an efficient correlation-type functional to address area-based registration, thus avoiding the significant computational burden associated with more complex information-theoretic functionals. Accordingly, the proposed method consists of two processing stages, associated with the domain adaptation (see Section 2.1.1) and area-based matching processes (see Section 2.1.3). In this way, the computational complexity of the multisensor registration problem is moved from the evaluation of the functional to the domain adaptation stage performed through the cGAN. A relevant advantage is that this high computational cost is paid offline during the training procedure of the cGAN, while it can be avoided at runtime when the trained cGAN is applied for prediction purposes. This approach also favors scalability to large datasets.

The cGAN is composed of two convolutional neural networks (CNNs), and its input samples are image patches drawn from the optical and SAR sources. The cGAN acts on the input image patches in different ways within its training and prediction phases. First, during the training phase, pairs of correctly registered optical-SAR patches are necessary to train the cGAN. They are needed to evaluate the loss function and optimize the parameters of the generator and discriminator. Accordingly, an assumption of the proposed multisensor registration approach is that correctly registered optical-SAR patches are available for this training step. Operatively, this implies that, given the optical and SAR data sources whose images we wish to register, we assume that some multisensor image data have been manually registered so that pairs of image patches have been extracted from them to train the neural model. Then, when the proposed approach is applied to register an input pair of optical-SAR images, the discriminator is discarded, and only the generator is used. In this prediction phase, obviously, no registered input pair is necessary.

In particular, in the proposed method, the generator is trained to estimate a “fake SAR” image starting from the input optical image, as shown in Figure 1. The rationale is twofold.

First, considering the dimension of the input feature space as compared to the dimension of the target space that should be estimated by the generator, this translation process is expected a priori to be more effective than in the opposite direction. Indeed, optical multispectral data typically come with a higher number of channels than SAR imagery, which includes one band in the case of single-frequency single-polarization SAR and a few channels in the cases of multi-frequency and/or polarimetric SAR. While in the specific case of panchromatic-to-SAR translation, this setting yields no specific advantage, in the general case of multispectral-to-SAR translation, it favors an easier mapping from the higher-dimensional feature space of the multispectral channels to the lower-dimensional feature space of the SAR channels than vice versa, since the information coming from several optical bands can be used to estimate a single SAR band. We also recall that experimental evidence of the increased effectiveness of translating optical to SAR rather than vice versa has already been reported in the literature [4]. Furthermore, preliminary tests, not shown here for brevity, have confirmed this finding from the literature and shown that optical-to-SAR translation through the considered cGAN architecture leads to a “fake SAR” images that resemble the true counterpart more closely than the “fake optical” generated in the opposite configuration.

Second, the use of a single-band output from the generator is convenient within the registration stage of the proposed algorithm, which makes use of a similarity functional whose input is intrinsically scalar (see Section 2.1.3). The extension of the registration stage to input multiple bands would generally require a case-specific reformulation of the similarity functional aimed at operating with input vector-valued imagery, which could generally lead to increased computation time.

In the application of the proposed method, it is also assumed that the optical and SAR images are defined on the same pixel grid. If these input images share the same spatial resolution, this assumption is naturally satisfied. Otherwise, it is assumed that the image at the finer spatial resolution has been downsampled on the pixel grid of the image at the coarser resolution as a preprocessing step. The implications of this step are twofold. First, it allows satisfying one of the requirements of the cGAN procedure, for which the input and target images are supposed to share the same pixel lattice. Second, since the input images to be registered are supported on the same pixel grid, it is straightforward to define constraints on possible scale parameters of the geometric transformation, bounding them in a neighborhood of one. This is advantageous in terms of computational time because it limits the size of the search space for the vector of transformation parameters. Furthermore, this choice allows for fixing possible reprojection errors in a neighborhood of the unitary scale parameter.

2.1.1. Conditional GAN Stage

The domain adaptation step is achieved using the pix2pix cGAN architecture in [8]. Let $\mathcal{R}$ and $\mathcal{S}$ be the optical (multispectral or panchromatic) and the SAR images to be registered, respectively. We assume that $\mathcal{R}$ and $\mathcal{S}$ have been acquired over the same ground area, and we denote $\mathit{r}$ and $\mathit{s}$ as the optical and SAR data samples, respectively. The vectors $\mathit{r}$ and $\mathit{s}$ collect the intensities of the pixels belonging to image patches associated with the same location in the images $\mathcal{R}$ and $\mathcal{S}$, respectively. The cGAN model is composed of two CNNs that formalize a mapping G (generator) from an optical patch $\mathit{r}$ to an estimated SAR patch $\widehat{\mathit{s}}$ and a mapping D (discriminator) from a candidate SAR patch to the interval $(0,1)$. The discriminator is aimed at distinguishing if the input SAR patch is coming from an actual SAR image (“true”; output of D close to 0) or has been estimated by the generator from an input optical patch (“fake”; output of D close to 1). Conversely, the generator is aimed at producing output SAR patches that are accurate enough to fool the discriminator. This adversarial behavior is formalized through the following loss function [8]:

$$\mathcal{L}(D,G)={\mathbb{E}}_{\mathit{r},\mathit{s},\mathit{z}}\left\{lnD(\mathit{r},\mathit{s})+ln[1-D(\mathit{r},\widehat{\mathit{s}})]+\lambda \left|\right|\mathit{s}-\widehat{\mathit{s}}{\left|\right|}_1\right\},$$

(2)

where:

$$\widehat{\mathit{s}}=G(\mathit{r},\mathit{z})$$

(3)

and where $\mathit{z}$ is a dropout noise [66]. Let $\widehat{\mathcal{S}}$ be the image obtained in the output of the generator when it is fed with the input optical image $\mathcal{R}$. The additional ${\ell }^1$ loss in (2) (i.e., the term $\left|\right|\mathit{s}-\widehat{\mathit{s}}{\left|\right|}_1$) favors the structural similarity between the generated image $\widehat{\mathcal{S}}$ and the target image $\mathcal{S}$. $\lambda$ is a positive coefficient weighing the adversarial and ${\ell }^1$ terms in the loss functions. The training of the cGAN is accomplished through the optimization of the loss function $\mathcal{L}$ with respect to the parameters of both networks D and G. In particular, consistently with the adversarial formulation, $\mathcal{L}$ is minimized with respect to the network parameters of G and maximized with respect to those of D. Details on the architecture, and its training can be found in [8].

It is worth noting that the proposed cGAN is applied to image patches and not to the entire input image. This is due to the fact that the pix2pix network has been designed to work with small input images (e.g., $256\times 256$ pixels).

2.1.2. Transformation Stage

In the proposed method, we focus on the RST family, which encompasses translations, rotations, and scaling. As compared to larger families of transformations (e.g., affine or polynomial), RST models often represent an effective trade-off between the generality of the transform and the dimensionality of the parameter space where the optimal transform is sought for (four parameters for RST). In any case, the focus on the RST family is not a restriction in the proposed approach, whose combination with other parametric families of geometrical transformations is straightforward.

Having the shear angle equal to zero $(\varphi =0)$ and the scale parameters equal in the two dimensions $(k_x=k_y=k)$, the transformation T in (1) becomes:

$$\begin{array}{c}\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& -T_x\\ 0& 1& -T_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}k& 0& 0\\ 0& k& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos\left(\theta \right)& -sin\left(\theta \right)& 0\\ sin\left(\theta \right)& cos\left(\theta \right)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right],\end{array}$$

(4)

where $T_x,T_y\in \mathbb{R}$, $0\le \theta \le 2\pi$, and $k>0$. Here, $(x,y)$ and $(X,Y)$ are meant as the coordinate systems of the spatial lattices of the SAR and optical images, respectively. The geometrical transformation is applied together with nearest neighbor resampling [67] to ensure that the transformed image only contains intensity values that were present in the original image.

It is worth noting that the transformations considered in the proposed approach are meant as global, i.e., they operate on the entire image or, at least, on an image patch of non-negligible size. The extension to the non-global case can be achieved by considering a series of different transformations applied to separate image patches, obtaining a piece-wise linear global transformation [68].

2.1.3. Matching Strategy

In the proposed registration method, a simple ${\ell }^2$ area-based similarity measure is selected to guide the search for the optimal geometric transformation:

$$C\left(T\right)={〈s\left[T(·)\right],\widehat{s}〉}_{{\ell }^2}=\sum _{X,Y}s\left[T(X,Y)\right]\widehat{s}(X,Y),$$

(5)

where the sum is extended over all pixel coordinates $(X,Y)$ in the lattice of the optical image. $C\left(T\right)$ measures the similarity between the output $\widehat{\mathcal{S}}$ of the generator, which is obtained from the input optical image $\mathcal{R}$ and is consequently supported on its pixel lattice $(X,Y)$, and the original SAR image $\mathcal{S}$ transformed through T. Operatively, $C\left(T\right)$ is the ${\ell }^2$ inner product between the function $\widehat{s}(·)$ and the composite function $s\left[T\right(·\left)\right]$, both defined on the pixel lattice of $\mathcal{R}$. These two functions express the pixel intensities in $\widehat{\mathcal{S}}$ and in the output of the geometric transformation of $\mathcal{S}$, respectively. This formulation implies that, in the proposed method, the optical image $\mathcal{R}$—together with the resulting estimated SAR image $\widehat{\mathcal{S}}$—is assumed as the reference image, whereas the SAR image $\mathcal{S}$ is the input image to be transformed to achieve registration.

$C\left(T\right)$ is also proportional to evaluating, in the origin, the sample cross-correlation function between the output $\widehat{\mathcal{S}}$ of the generator and the transformation of $\mathcal{S}$ through T and can be computed very efficiently. Whereas the cross-correlation functional is typically ineffective for multisensor registration, its role in the proposed method and the resulting time efficiency are made possible by the domain adaptation performed through the cGAN. The optimal transformation is searched for by maximizing $C\left(T\right)$ with respect to the transformation parameters $(T_x,T_y,\theta ,k)$. Indeed, C is generally a non-differentiable function of these parameters; hence a maximization method that does not require derivatives is necessary. Among derivative-free optimization algorithms, COBYLA (constrained optimization by linear approximation) is adopted as a usually accurate and efficient approach [10].

COBYLA addresses constrained optimization by linear approximations. It works by iteratively approximating the actual constrained optimization problem with a sequence of linear programming problems. At each iteration, the resulting linear programming problem is solved to obtain a candidate for the optimal solution. The candidate solution is evaluated using the original objective and constraint functions, yielding a new data point in the optimization space. This information is used to improve the approximate linear programming problem used for the next iteration of the algorithm. When no improvement is possible, the step size is reduced, refining the search. When the step size becomes sufficiently small, the algorithm stops [10]. In the application to $C(·)$, box constraints can easily be predefined without loss of generality: $\theta$ takes values in $[0,2\pi ]$, $T_x$ and $T_y$ can be bounded according to the sizes of $\mathcal{R}$ and $\mathcal{S}$, and the bounds on k can be defined as a function of their spatial resolutions. In particular, in the proposed method, thanks to the assumption that the input and reference images are supported on the same pixel lattice, the scale parameter k is used to account for small scale variations and bounded in the range $[0.98;1.02]$.

COBYLA includes a hyperparameter $\rho$ that indicates an initial search radius [10]. In the proposed multisensor registration method, this hyperparameter is automatically optimized through a dictionary approach. A finite dictionary $\mathcal{D}$ of increasing radius values is predefined, and COBYLA is run separately for each $\rho \in \mathcal{D}$ leading to a candidate solution $T_{\rho }^{*}$. Each one of these solutions is assessed in terms of the value $C\left(T_{\rho }^{*}\right)$ of the objective function $C(·)$ to be maximized, and the one providing the highest matching value is selected as the output transformation.

2.2. Data Sets for Experiments

The proposed approach has been experimentally validated with three multisensor datasets.

(1)

Paraguay: The dataset is composed of Sentinel-1 (S1) SAR and Sentinel-2 (S2) optical data acquired in 2018 over Amazonia. The study area is north of Pozo Colorado, Paraguay, west of the namesake river, and is mainly composed of grass, crops, forests, and waterways. S2 provides multispectral data with 13 bands in the visible, near-infrared (NIR), and short wave infrared. The spatial resolution includes 10, 20, and 60 m depending on the bands, with 10 m available for the blue, green, red, and NIR channels. The spatial resolution of S1 is 5 m in stripmap mode.

(2)

Bussac: The second dataset is made of a Pléiades panchromatic image and a COSMO-SkyMed SAR image acquired in Spotlight mode on an ascending orbit over a countryside area near Bussac-Forêt, France. The study zone is composed of woods, fields, roads, and a few buildings. The radar image is acquired in the right-looking direction and has pixel spacing of 0.5 m, while the spatial resolution is approximately 1 m. The resolution of the panchromatic image is 0.5 m. The optical image has been projected into the radar geometry using the ALOS digital elevation model for the area of Bussac-Forêt.

(3)

Brazil: The third dataset is composed again of S1 and S2 data, acquired in 2018 over the Amazon. The area is over the city of Aquidauana, in the namesake region in Brazil. The landscape is composed of the city of Acquidauana, crops, forests, and some mountainous reliefs. The data composition is the same as in the Paraguay dataset. The proposed method, trained with the S1 and S2 data of the Paraguay dataset, was applied to this further dataset for testing purposes in order to investigate the robustness of an already trained model to variations in the distribution of the input data, provided they were acquired by the same sensors.

3. Results

3.1. Preprocessing and Setup

(1)

Paraguay: The red, green, and NIR optical channels with 10 m spatial resolution were considered for experiments. The input SAR data were obtained by applying the multitemporal despeckling method in [69] to a time series of seven S1 acquisitions. According to the assumptions of the proposed approach, the optical and SAR images to be registered are supposed to share the same pixel lattice. The Paraguay dataset corresponds to optical-SAR pairs with different spatial resolutions. S1 stripmap imagery and S2 visible and NIR channels have 5 and 10 m resolutions, respectively. Therefore, as a preprocessing step, the S1 input was downsampled on the pixel lattice of the S2 image prior to the application of the proposed method. The S2 and the despeckled SAR images were manually registered to be used for training the cGAN and testing the proposed method. The training set was composed of 187 patches ($512\times 512$ pixels each) drawn from the East part of the scene. The number of training epochs was set at 250.

(2)

Bussac: The final SAR image was obtained by averaging the results of two different despeckling techniques applied to the COSMO-SkyMed image: a Wiener filter applied with a homomorphic filtering strategy (logarithmic scale) and the method in [70], which applies non-local filtering by means of wavelet shrinking. No resampling was necessary in the case of the Bussac dataset because the spatial resolution of the Pléiades panchromatic image is equal to the pixel spacing of the COSMO-SkyMed Spotlight image ($0.5$ m). The entire COSMO-SkyMed image was approximately $5500\times 5500$ pixels, and around 75% of the scene was used to train the cGAN. The Pléiades panchromatic image was manually warped to the SAR grid, so there were paired patches to be used for training. Even after this manual step, the images could still exhibit residual subpixel error. The training set was made of 101 patches ($512\times 512$ pixels each) drawn from the whole scene except for the southwest corner, which was used for testing the accuracy of the registration result. In this case, the default architecture of pix2pix, which is aimed at operating with 3-channel imagery, was modified to map from the single-channel panchromatic to the single-channel SAR domains. The number of training epochs was experimentally fixed at 200. The amount of training data was, in fact, rather limited, so it was important to minimize the risk of overfitting.

(3)

Brazil: In this case, the data are of the same kind of those in Paraguay. The same preprocessing strategy as in the case of the Paraguay dataset was adopted. Here, the S2 and the despeckled SAR images were manually registered only for testing purposes since the cGAN trained on the Paraguay dataset was considered here, without any fine-tuning or retraining.

In the cases of all the three datasets, the histograms of the related images were stretched by saturating 1% of their tails in order to simplify the adaptation operations performed by the cGAN.

3.1.1. Hyperparameter Tuning

The default architecture of pix2pix was used with the adaptation that the filter size was changed to $5\times 5$ to consider that, even if registered, the images could exhibit residual subpixel errors. The training time on a Tesla K80 GPU was about 8 hours and 3 hours for the Paraguay and Bussac datasets, respectively. The dictionary used for the optimization of the hyperparameter $\rho$ in COBYLA was $\mathcal{D}=\{20,30,40,50,60\}$. The weight parameter $\lambda$ of pix2pix was set based on the original paper [8].

3.1.2. Competing Methods

The results obtained by the proposed method were compared to those coming from state-of-the-art area-based approaches based on the MI functional. In particular, the MI between the original SAR image and the NIR band of the optical image was maximized as a function of the parameters of an RST transformation using either COBYLA or Powell’s algorithm.

COBYLA has been recalled in Section 2.1.3. The unconstrained Powell’s algorithm uses Powell’s formulation of an approximate conjugate gradient method. The objective function does not need to be differentiable, and no derivatives are required [10] (differently from the standard conjugate gradient algorithm). The method performs a sequence of line searches along a set of vectors that emulate the conjugate gradient vectors without using derivatives [71]. Each line search is accomplished through the golden section and Brent’s methods [72]. Here, Powell’s algorithm was applied both in its classical unconstrained formulation and together with barrier functions [73]. The latter option was aimed at implementing the same box constraints used with COBYLA.

3.2. Experimental Results

First, in order to quantitatively compare the different methods, an experiment with semi-simulated data was performed. For each dataset, the SAR and optical images were first registered using manual tie points. Then, four RST transformations were applied with rotations ranging from 1.4° to 2.5°, a scale factor of 1.01, and translations from 25 to 45 pixels in each dimension. The parameters $(T_x,T_y,\theta ,k)$ of these four transformations (which were numbered from 1 to 4) were $(45,40,2.5,1.01)$, $(45,40,1.8,1.01)$, $(30,-25,1.6,1.01)$, and $(-30,40,1.4,1.01)$. Given the manually registered optical and SAR images, each synthetic transformation was applied to the SAR image. Then, the proposed and the competing methods were applied to the resulting misregistered pair by initializing the optimization methods with the identity transformation $(0,0,0,1)$. In this case, a true transformation (which will be referred to as ”ground truth” transformation) existed, and the root mean-square error (RMSE) could be quantitatively evaluated [74]. The initial RMSEs, which quantify the registration error after the synthetic transformations were applied, are shown in

Table 1. RMSE in pixels for the Paraguay dataset (area1/area2) and four test transformations.

Synthetic Transformation	Initial	Powell	Mutual Information Powell with Barrier Functions	COBYLA	Proposed
1	111.02	1.24/743	0.95/1.05	2.34/0.9	0.34/0.35
2	96.38	1.06/739	0.92/0.9	2.29/3.82	0.24/0.22
3	88.92	61.7/0.93	61.8/0.98	18.4/13.5	0.22/0.42
4	34.37	35.5/1.36	39.4/1.07	1.01/4.14	0.22/0.27
avg.	82.67	24.9/371	25.7/1	6.01/5.59	0.25/0.31

,

Table 2. RMSE in pixels for the Bussac dataset and four test transformations.

Synthetic Transformation	Initial	Powell	Mutual Information Powell with Barrier Functions	COBYLA	Proposed
1	111.02	52.08	18.7	21.55	0.87
2	96.38	32.52	38.1	20.78	0.81
3	88.92	14.55	18.93	26.35	0.85
4	34.37	71.75	53.83	17.87	0.89
avg.	82.67	42.72	32.48	21.63	0.85

and

Table 3. RMSE in pixels for the Brazil dataset (area 1/ area2) and four test transformations.

Synthetic Transformation	Initial	Powell	Mutual Information Powell with Barrier Functions	COBYLA	Proposed
1	111.02	863/88.68	1.10/90	2.57/6.93	1.08/0.89
2	96.38	1.21/0.97	38.1/38.1	4.54/1.31	1.07/0.95
3	88.92	0.83/1.25	0.63/1.34	11.3/16.6	1.09/1.07
4	34.37	0.42/1.4	1.45/1.2	3.97/0.84	1.08/0.91
avg.	82.67	14.2/22.9	10.3/23.3	5.61/6.43	1.08/0.96

. The same synthetic transformations are used in the case of all datasets, so the values of these initial RMSEs are the same in all three tables.

Then, in the case of the Paraguay dataset, a further experiment involving the registration of a real pair of initially mismatched S1–S2 images was performed. In this case, the goal was to assess the proposed method in its application to a fully real dataset, although the registration performances could be assessed only qualitatively because no “ground truth transformation” was available.

3.2.1. Results from the Paraguay Dataset

On the Paraguay dataset, two test areas were drawn from the west part of the scene. Such areas were disjoint from all training patches and were approximately $1400\times 1400$ pixels each. The results of the domain adaptation step performed by the cGAN are shown in Figure 2.

The registration results in terms of RMSE obtained by the proposed and previous methods are shown in Table 1. The initial error indicated in this table is the RMSE between the optical and SAR images before the registration.

Figure 3 shows the results of the proposed method by superimposing the images before and after registration. The upper panel regards test area #1, while the lower panel shows test area #2. In the displays, the true and estimated SAR images are overlaid in a false-color composite.

As mentioned above, in addition to the aforementioned experiments with semi-simulated data, an experiment with fully real data was also conducted with the Paraguay dataset. The proposed method was applied to the registration of an additional SAR image obtained through the multitemporal despeckling of S1 acquisitions collected in a season different from that of the data used for training. This third test area, which was partially overlapping with one of the two areas used in the semi-simulated case, was also meant to test robustness since the different seasons of acquisition inherently yielded discrepancies not only in the way the data were acquired but in the ground scene itself, especially in the details of the spatial features such as the size and shape of the crops and the quantity of water within the river beds. In this experiment with fully real data, quantitative error figures could not be calculated, but registration accuracy could be evaluated visually. The results are shown in Figure 4. In this case, two displays are used. In the first one, corresponding to the top row of the figure, the true and estimated SAR images are overlaid in a false-color composite. In the second one, shown in the bottom row, the SAR image and the NIR channel of the optical image are composed of a checkerboard pattern whose squares come from the two images alternately.

3.2.2. Results on the Bussac Dataset

Regarding the Bussac dataset, a single test area was drawn from the southwest part of the scene. The area was completely disjoint from all the training patches. Its size was $2200\times 2200$ pixels, larger than the test areas of the Paraguay dataset. Considering the finer resolution of the dataset, this choice was to make sure that a significant amount of spatial features from the considered scene was included in the test region. Figure 5 shows the results of the domain adaptation performed by the cGAN.

Table 2 shows the RMSEs obtained from the Bussac dataset. The visual overlays before and after registration are shown in Figure 6.

3.2.3. Results on the Brazil Dataset

In this case, the experiment was aimed at evaluating the performance of the proposed method when trained with a given training set and applied to a separate dataset, which was acquired by the same sensors (i.e., S1 and S2) but could generally exhibit different distributions due to the distinct geographical areas. On the one hand, this configuration constitutes a challenging scenario for a supervised neural approach since the data used for prediction purposes do not generally share the same distribution as the data used to train the network. Accordingly, decreased performance can be expected in the estimation of a fake SAR image from the optical one through the cGAN. On the other hand, this experiment allows investigating the applicability of the proposed cGAN-based approach to the registration of multisensor image data collected by the same sensors of the data used for training purposes but in a significantly different ground region. The output generated through the cGAN is shown in Figure 7.

The RMSE obtained by the proposed method and the previous approaches is presented in Table 3.

Figure 8 shows the visual overlays before and after registration.

4. Discussion

4.1. Paraguay Results

In terms of visual comparison, the accuracy of the domain adaptation performed by the cGAN can be appreciated in Figure 2, where significant discrepancies between the true and fake SAR images are hard to detect even through visual analysis. This suggests the effectiveness of the considered cGAN architecture in emulating SAR data from input optical data, at least in the case of the considered dataset. It is also worth noting that, to apply the cGAN, first, each test area was split into non-overlapping patches of size $512\times 512$ pixels, then the cGAN was separately applied to each patch, and finally, the cGAN outputs obtained from the individual patches were recombined. Indeed, the accuracy of the adaptation is also confirmed by the fact that, in Figure 2, border effects between adjacent patches are barely visible in the recombined image.

Regarding the registration results in terms of RMSE, the scores obtained by the different methods in the case of the Paraguay dataset are shown in Table 1. The state-of-the-art method using Powell’s algorithm obtained results characterized by a large overall variability in the RMSE as a function of the considered synthetic transformation. For some transformations, this method achieved RMSE values around 1 pixel (down to a minimum of 0.9 pixels). However, in the cases of other transformations, the method converged to poor solutions, sometimes even characterized by higher RMSE values than before registering. The constrained version of Powell’s technique, applied to maximize MI, achieved an RMSE of around 1 pixel in the second test area for all the four considered transformations. On the contrary, its results in the first test area again exhibited a significant variability. The results obtained maximizing MI with COBYLA exhibited less variability, but the average RMSE was still of some pixels. On the contrary, the proposed method obtained stable results with subpixel error and low variability in both test areas ($\mathrm{RMSE}$ was always in the range from $0.22$ to $0.42$ pixel). These results suggest the effectiveness of integrating the cGAN with a correlation-type functional and with COBYLA as compared to the area-based approach based on the maximization of the MI.

The visual analysis of Figure 3 confirms an apparently negligible registration error. This is evident from the superposition in the false-color visualization. In particular, the accuracy of the registration can be qualitatively appreciated by looking at the matching of the spatial features that are present in both test areas, i.e., crops and rivers.

With regard to the experiment with fully real data, comparing the before and after-registration displays in Figure 4, a visual analysis points out that the developed method obtained a remarkable improvement in spatial alignment. These results not only confirm the effectiveness of the developed technique in its application to real data as well but also suggest its robustness to inherent differences in the input data. Most of the residual mismatch that can be noted around certain edges is interpreted as a minor impact of the different seasonality of the images used in the training and prediction phases and of the resulting ground changes. This is evident in the bottom panel of Figure 4, where the checkerboard allows the inherent differences to be clearly noticed.

4.2. Bussac Results

The visual comparison in Figure 5 indicates that in the case of the Bussac dataset as well, most spatial features were well represented by the domain adaptation result. Yet, this result is not as visually accurate as in the case of the Paraguay dataset. Several areas exhibit different average grey levels in the true and fake SAR images, and the spatial features and patterns are not perfectly reproduced. An example can be noticed in the darker area in the middle of the upper-right part of Figure 5, which is not correctly represented, or in the areas covered by trees whose patterns are not well reproduced by the cGAN. This is interpreted in relation to the high resolution of the input images together with the land cover of the observed area, which is primarily composed of trees. Indeed, the canopy is imaged by optical and SAR sensors through highly different physical and geometrical processes, thus making for an especially challenging scene to be reproduced through a cGAN [4].

However, notwithstanding the reduced visual accuracy of the adaptation results on the Bussac dataset, as compared to those on the Paraguay dataset, the proposed registration method obtained accurate results in the Bussac case, too. In particular, while state-of-the-art methods struggled on this dataset, the proposed method obtained subpixel RMSE in the case of all considered transformations (see Table 2). Maximizing MI with the unconstrained Powell’s method, with Powell’s method with barrier functions, and with COBYLA led to average RMSE values equal to 42.72, 32.48, and 21.63 pixels, respectively. Such values were remarkably smaller than the errors between the optical and SAR images before the registration was performed, thus suggesting that the considered previous approaches significantly reduced the spatial mismatch in the case of this challenging dataset. However, more accurate registration results were generated by the proposed approach in the case of all considered transformations.

These comments are confirmed by the false-color overlays for the Bussac dataset (see Figure 6), which show a rather evident improvement achieved by the proposed method as compared to the pair of input images before registration. Indeed, the main spatial features that were mismatched in the before-registration display are superimposed in the after-registration display well.

In the case of the Bussac dataset, accurate registration was obtained by the proposed approach even though the fake SAR images exhibited non-negligible differences from the true SAR data. In this respect, we recall that, within the proposed method, the cGAN-generated SAR image is aimed at being used within the registration step of the method itself and not at being utilized in further remote sensing applications. On the one hand, optical-to-SAR translation proves useful in other remote sensing data analysis tasks as well—most remarkably, for change detection [61,75]. On the other hand, should the cGAN-generated SAR image be used in the context of another application, a dedicated experimental validation would be necessary to evaluate the impact of the visual accuracy of the adaptation results in that framework.

4.3. Brazil Results

The application of the cGAN trained on the Paraguay dataset to the Brazil dataset provided visually rather good adaptation results. However, the reproduction of the SAR spatial field was substantially less accurate than when the cGAN was applied to the test areas of the Paraguay dataset (see Figure 7). In particular, the borders among the individual patches processed by the cGAN are visible, which points out a higher instability in the domain adaptation results. These border effects were mitigated by feeding the cGAN with partially overlapping patches. However, residual edges can be seen in Figure 7, especially on the right part. Moreover, while the main spatial features were well reproduced, the average grey level of several regions was slightly different in the true and fake SAR images. These results are consistent with the different distributions of the images involved in the training and prediction phases of the cGAN.

Nevertheless, the RMSE values obtained by the proposed method and the competing methods on the Brazil dataset (see Table 3) were in line with those obtained in the case of the Paraguay dataset. The state-of-the-art method using Powell’s algorithm obtained results characterized by an overall high variability. In the case of some initial transformations, it obtained subpixel RMSE (down to a minimum of $0.42$ pixel), but in other cases, the method failed to find an appropriate solution. While minimizing MI with COBYLA obtained more stable results again, the average RMSE was again of a few pixels. On the contrary, the proposed method again generated registration results with an RMSE around 1 pixel in the case of all considered transformations. This suggests that, despite the suboptimal image-to-image translation results, the overall developed method could still benefit significantly from the cGAN output to achieve accurate registration through the maximization of a simple ${\ell }^2$ similarity measure.

These comments are confirmed by a visual analysis of the corresponding images (see Figure 8). On the one hand, the aforementioned issues in the domain adaptation results can also be visually appreciated in the false-color overlays, in which it is possible to notice some areas that were not correctly translated; on the other hand, these overlays indicate a visually precise alignment in this case as well.

5. Conclusions

In this paper, a novel registration method for multisensor optical-SAR images has been proposed. It integrates a cGAN architecture within an area-based registration framework involving an ${\ell }^2$ similarity measure and the COBYLA nonlinear optimization algorithm.

Experimental results with three datasets, acquired from different locations and at different spatial resolutions, suggest the capability of the proposed method to achieve accurate registration. When applied to semi-simulated data, for which the true “ground truth” transformation is known, the proposed technique has generated output results characterized by root mean square errors smaller than or approximately equal to one pixel. These results suggest the effectiveness of the proposed integration of a cGAN model and of an ${\ell }^2$ similarity measure when addressing the challenging problem of multisensor optical-SAR image registration. This effectiveness is also confirmed by the visually accurate registration obtained in the application to a fully real dataset made of input multisensor images collected in different seasons.

The developed method has also proven to be robust to variations in the input distribution and to be applicable to similar yet heterogeneous cases without the need for retraining. Specifically, the method makes use of a supervised approach, i.e., it requires an input set of registered optical-SAR image patches to be used to train the cGAN. Indeed, this characteristic represents the main operational limitation of the proposed approach. However, it is worth noting that, in a dedicated experiment with Sentinel-1 and 2 images, the proposed technique, trained with multisensor data of a given area, has achieved accurate registration even when applied to multisensor images of a different geographical region. This suggests that, at least in the case of the considered datasets, the proposed approach is applicable to register images of areas unrelated to the training set, provided that the same optical-SAR image sources are involved.

In the case of all considered datasets, the proposed technique has outperformed previous area-based approaches that combine an information-theoretic functional with different nonlinear optimization algorithms. While the aforementioned state-of-the-art methods have achieved results comparable to those of the developed technique in a few cases, they also have obtained significantly larger errors in many other runs. In general, their results have exhibited a high variability as a function of the considered image transformation. This scenario suggests a trade-off between the proposed approach and these previous algorithms in terms of registration performance and training data requirements. On the one hand, these benchmark techniques do not make use of a supervised approach and, therefore, do not involve input registered optical-SAR patches for training purposes. On the other hand, the developed method yields significantly smaller errors than these previous algorithms, thus suggesting the potential of the adopted supervised image-to-image translation approach to multisensor registration.

Remarkably, the simple correlation-type functional adopted in the method, which is usually ineffective in the application of multisensor image registration due to the inherently different characteristics of the input imagery, prove effective within the proposed approach. This is due to the combination with the powerful image-to-image translation capabilities of the cGAN. The domain adaptation step performed by the cGAN allows moving the computational complexity of the registration from the computation of the matching function to the training of the network itself. In this way, the major computational cost of the proposed method is dealt with in the offline phase. Once the cGAN is trained, the runtime computational cost is low.

Among the lessons learned from the experiments, we first recall the confirmation of the potential of generative adversarial methods in the application to area-based registration of multisensor optical-SAR imagery. This could not be taken for granted in the first place, both due to the challenge of this multisensor registration task and the fact that previous attempts to use GAN-type models in this context made use of feature-based and not area-based registration. Indeed, the experimental validation conducted in the paper pointed out the small RMSE values achieved by the proposed area-based generative-adversarial approach to optical-SAR image registration. A further—more specific—lesson learned is that stretching the histograms of the related images by saturating 1% of their tails is useful for reducing the complexity of the translation process. Analogously, the search for the optimal geometrical transformation has taken benefit from the assumption that the optical and SAR images are supported on the same pixel lattice and from the use of tight constraints on the scale parameter k. These properties allow bounding the search space, thus simplifying the optimization process.

Future generalizations of the proposed approach may include the extension with cyclic GANs [76] in order to remove the need for paired patches for the training of the networks. Another aspect worth investigating is the integration of the matching functional within the loss function of the neural model itself. Furthermore, after the cGAN is trained, the proposed approach involves the application of the generator for prediction purposes and the maximization of the ${\ell }^2$ similarity measure—both processing steps being computationally efficient. This efficiency suggests combining the proposed technique with image tiling and mosaicing operations to favor scalability and applicability to large-scale areas [68].