Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar
Abstract
:1. Introduction
2. STAP Algorithm in HFSWR
2.1. Signal Model and Basic Principle of STAP in HFSWR
2.2. Performance Analysis of STAP with Main-Lobe Clutter Component
3. Sparse Representation of the Space-Time Clutter Spectrum
4. Proposed Method
4.1. Eigen-Projection Matrix Preprocessing Method
4.2. Space-Time Beam Pattern Reshaping
4.3. Algorithm
| Algorithm 1. Beam Reshaping |
|
5. Simulation Results
5.1. Simulation Data
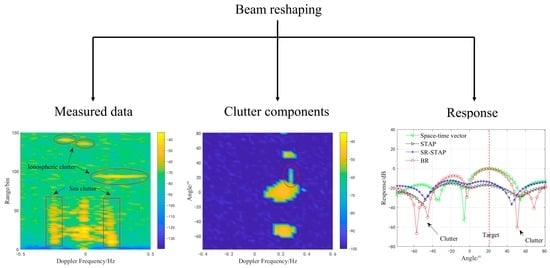
5.2. Measured Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Zhang, W.; Li, M.; Niu, J.; Wu, Q.M. Automatic detection of ship targets based on wavelet transform for HF surface wavelet radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 714–718. [Google Scholar] [CrossRef]
- Barrick, D.E. History, Present Status, and Future Directions of HF Surface-Wave Radars in the U.S. In Proceedings of the 2003 International Conference on Radar (IEEE Cat. No. 03EX695), Adelaide, Australia, 3–5 September 2003. [Google Scholar]
- Ponsford, A.; Mckerracher, R.; Ding, Z.; Moo, P.; Yee, D. Towards a cognitive radar: Canada’s third-generation high frequency surface wave radar (HFSWR) for surveillance of the 200 nautical mile exclusive economic zone. Sensors 2017, 17, 1588. [Google Scholar]
- Luo, Z.; He, Z.; Chen, X.; Lu, K. Target location and height estimation via multipath signal and 2D array for sky-wave over-the-horizon radar. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 617–631. [Google Scholar] [CrossRef]
- Chen, S.Y.; Gill, E.W.; Huang, W.M. A high-frequency surface wave radar ionospheric clutter model for mixed-path propagation with the second-order sea scatter. IEEE Trans. Antennas Propag. 2016, 64, 5373–5381. [Google Scholar] [CrossRef]
- Jiang, W.; Deng, W.B.; Shi, J.L. Characteristic Study of Ionospheric Clutter in High-Frequency over the Horizon Surface Wave Radar. In Proceedings of the IEEE Youth Conference on Information, Computing and Telecommunication, Beijing, China, 20–21 September 2009. [Google Scholar]
- David, K.B.; Leonov, S.A. Radar Technology Encyclopedia; Barton, D., Leonov, S.A., Eds.; Artech House Press: Norwood, MA, USA, 1997; Volume 3, pp. 310–311, ISBN-13 978-1580532594. [Google Scholar]
- Hua, X.; Ono, Y.; Peng, L.; Cheng, Y.; Wang, H. Target detection within nonhomogeneous clutter via total Bregman divergence-based matrix information geometry detectors. IEEE Trans. Signal Process. 2021, 69, 4326–4340. [Google Scholar] [CrossRef]
- Hua, X.; Peng, L. MIG median detectors with manifold filter. Signal Process. 2021, 188, 108176. [Google Scholar] [CrossRef]
- Hua, X.; Ono, Y.; Peng, L.; Xu, Y. Unsupervised Learning Discriminative MIG Detectors in Nonhomogeneous Clutter. IEEE Trans. Commun. 2022, 70, 4107–4120. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.; Xu, R. An ionospheric Es layer clutter model and suppression in HF surfacewave radar. Int. J. Antennas Propag. 2013, 2013, 141–169. [Google Scholar] [CrossRef]
- Brennan, L.E.; Reed, L.S. Theory of adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 1974, 9, 853–863. [Google Scholar] [CrossRef]
- Ravan, M.; Saleh, O.; Adve, R.S. KB-STAP Implementation for HFSWR; Final Report for Defense Research and Development Canada; w7714-060999/001/SV; Dept. of Electrical and Computer Engineering University of Toronto: Toronto, ON, Canada, 2008; Available online: https://www.comm.utoronto.ca/~rsadve/Publications/FinalReport.pdf (accessed on 9 July 2021).
- Adve, R.S.; Hale, T.B.; Wicks, M.C. Practical joint domain localised adaptive processing in homogeneous and nonhomogeneous environments. Part 2: Nonhomogeneous environments. IEE Proc. Radar Sonar Navig. 2000, 147, 66–74. [Google Scholar] [CrossRef] [Green Version]
- Tang, B.; Tang, J.; Peng, Y. Detection of heterogeneous samples based on loaded generalized inner product method. Digit. Signal Process. 2012, 22, 605–613. [Google Scholar] [CrossRef]
- Rabideau, D.J.; Steinhardt, A.O. Improved adaptive clutter cancellation through data-adaptive training. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 879–891. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Zhang, X.; Guo, L.; Liang, C.; Bai, Y. A STAP clutter suppression algorithm based on sparse representation for small-array HFSWR. Remote Sens. Lett. 2022, 13, 611–620. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.; Wang, Y.; Wang, X. Direct data domain STAP using sparse representation of clutter spectrum. Signal Process. 2011, 91, 2222–2236. [Google Scholar] [CrossRef] [Green Version]
- Mohimani, H.; Babaie-Zadeh, M.; Jutten, C. A fast approach for overcomplete sparse decomposition based on smoothed norm. IEEE Trans. Signal Process. 2009, 16, 624–634. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Wang, Y.; Wan, S. Research of reshaping adapted pattern under mainlobe interference conditions. Mod. Radar 2002, 24, 50–55. [Google Scholar]
- Carlson, B.D. Covariance matrix estimation errors and diagonal loading in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 397–401. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, Q. Sidelobe suppression for robust Capon beamforming with mainlobe to sidelobe power ratio maximization. IEEE Antennas Wirel. Propag. Lett. 2008, 11, 1218–1221. [Google Scholar] [CrossRef] [Green Version]







| Parameter | Value |
|---|---|
| λ | 53.5 m |
| d | 14.5 m |
| Ne | 8 |
| Np | 512 |
| tm | 20.6 s |
| Doppler Frequency (Hz) | Angle | SNR/CNR (dB) | Main/Side Lobe | |
|---|---|---|---|---|
| Target | −1.116 | 0° | 20 | |
| Clutter component 1 | −1.116 | 9° | 23 | Main lobe |
| Clutter component 2 | −1.099 | 0° | 23 | Main lobe |
| Clutter component 3 | −1.116 | −39° | 20 | Side lobe |
| Clutter component 4 | −1.116 | 30° | 23 | Side lobe |
| Clutter component 5 | −0.825 | −39° | 20 | Side lobe |
| Clutter component 6 | −0.825 | 30° | 23 | Side lobe |
| Clutter component 7 | −1.309 | −6° | 23 | Side lobe |
| Parameter | Value |
|---|---|
| λ | 53.5 m |
| d | 14.5 m |
| Ne | 8 |
| Np | 1024 |
| tm | 41.2 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, Q.; Zhang, X.; Ji, X.; Xiao, D. Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar. Remote Sens. 2022, 14, 2935. https://doi.org/10.3390/rs14122935
Li J, Yang Q, Zhang X, Ji X, Xiao D. Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar. Remote Sensing. 2022; 14(12):2935. https://doi.org/10.3390/rs14122935
Chicago/Turabian StyleLi, Jiaming, Qiang Yang, Xin Zhang, Xiaowei Ji, and Dezhu Xiao. 2022. "Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar" Remote Sensing 14, no. 12: 2935. https://doi.org/10.3390/rs14122935
APA StyleLi, J., Yang, Q., Zhang, X., Ji, X., & Xiao, D. (2022). Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar. Remote Sensing, 14(12), 2935. https://doi.org/10.3390/rs14122935