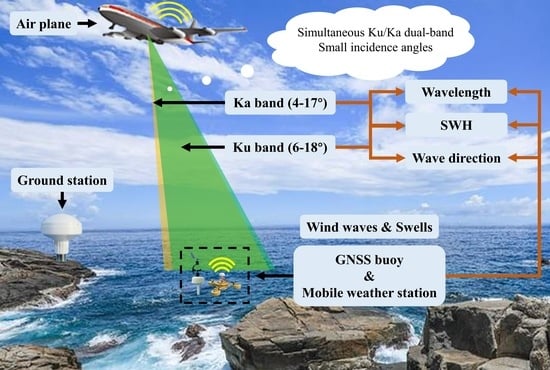
Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter
Abstract
:1. Introduction
2. Method
2.1. DInIRA Ocean Waves Inversion Methodology
2.2. The Airborne DInIRA Observation Campaign
2.3. Ocean Wave Inversion
3. Result
3.1. Ocean Wave Inversion Results
3.2. Verification Based on In situ Data
3.3. Accuracy Analysis of Ocean Wave Inversion Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OWPs | Ocean wave parameters |
| InIRA | Interferometric imaging radar altimeter |
| DInIRA | Dual-band interferometric imaging radar altimeter |
| WPD | Wave propagation direction |
| SWH | Significant wave height |
| MWW | Main wave wavelength |
| MWP | Main wave period |
| SSH | Sea surface height |
| EWD | Environmental wind direction |
| SAR | Synthetic aperture radar |
| OWS | Ocean wave spectra |
| InSAR | Interferometric SYNTHETIC APERTURE RADAR |
| DEM | Digital elevation model |
| XTI-SAR | Cross-track InSAR |
| SWOT | Surface water and ocean topography |
| FFT2 | 2D Fourier transform |
| SLC | Single look complex |
| SNR | Signal-to-noise ratio |
References
- Scharroo, R.; Bonekamp, H.; Ponsard, C.; Parisot, F.; von Engeln, A.; Tahtadjiev, M.; de Vriendt, K.; Montagner, F. Jason Continuity of Services: Continuing the Jason Altimeter Data Records as Copernicus Sentinel-6. Ocean Sci. 2016, 12, 471–479. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xu, H.; Yang, L.; Song, Q.; Ma, C. Cross-Calibrations of the HY-2B Altimeter Using Jason-3 Satellite During the Period of April 2019–September 2020. Front. Earth Sci. 2021, 9, 17. [Google Scholar] [CrossRef]
- Cai, Y.; Cheng, X.; Sun, G. A Review of Development of Radar Altimeter and Its Applications. Remote Sens. Inf. 2006, 4, 74–78. [Google Scholar]
- Macklin, J.T.; Cordey, R.A. Seasat SAR Observations of Ocean Waves. Int. J. Remote Sens. 1991, 12, 1723–1740. [Google Scholar] [CrossRef]
- Pramudya, F.S.; Pan, J.Y.; Devlin, A.T. Estimation of Significant Wave Height of Near-Range Traveling Ocean Waves Using Sentinel-1 SAR Images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 1067–1075. [Google Scholar] [CrossRef]
- Hasselmann, K.; Hasselmann, S. On the Nonlinear Mapping of An Ocean Wave Spectrum into a Synthetic Aperture Radar Image Spectrum and Its Inversion. J. Geophys. Res. Oceans. 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Engen, G.; Johnsen, H. SAR-ocean Wave Inversion Using Image Cross Spectra. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1047–1056. [Google Scholar] [CrossRef]
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Pottier, E. Measurement of Ocean Surface Slopes and Wave Spectra Using Polarimetric SAR Image Data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- Caponi, E.A.; Crawford, D.R.; Yuen, H.C.; Saffman, P.G. Modulation of Radar Backscatter from the Ocean by a Bariable Surface Current. J. Geophys. Res. 1988, 93, 12249. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lehner, S. Ocean Wave Imaging Using an Airborne Single Pass Across-track Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 38–45. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Horstmann, J.; Lehner, S.; Rosenthal, W. Sea Surface Imaging with an Across-track Inter-ferometric Synthetic Aperture Radar: The SINEWAVE Experiment. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2017–2028. [Google Scholar] [CrossRef]
- Quilfen, Y.; Chapron, B.; Bentamy, A.; Gourrion, J.; El Fouhaily, T.; Vandemark, D. Global ERS 1 and 2 and NSCAT Observations: Upwind/Crosswind and Upwind/Downwind Measurements. J. Geophys. Res.: Oceans. 1999, 104, 11459–11469. [Google Scholar] [CrossRef]
- Jackson, F.C.; Walton, W.T.; Baker, P.L. Aircraft and Satellite Measurement of Ocean Wave Directional Spectra Using Scanning-beam Microwave Radars. J. Geophys. Res.: Oceans. 1985, 90, 987–1004. [Google Scholar] [CrossRef]
- Rodriguez, E.; Pollard, B.; Martin, J. Wide-Swath Ocean Altimetry Using Radar Interferometry. IEEE Trans. Geosci. Remote Sens. 1999. Available online: http://hdl.handle.net/2014/17962 (accessed on 14 June 2022).
- Fjortoft, R.; Gaudin, J.M.; Pourthie, N.; Lalaurie, J.C.; Mallet, A.; Nouvel, J.F.; Martinot-Lagarde, J.; Oriot, H.; Bor-deries, P.; Ruiz, C.; et al. KaRIn on SWOT: Characteristics of Near-Nadir Ka-Band Interferometric SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2172–2185. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Dong, X.; Jia, Y.; Zhang, Y. Preliminary Significant Wave Height Retrieval from Interferometric Imaging Radar Altimeter Aboard the Chinese Tiangong-2 Space Laboratory. Remote Sens. 2021, 13, 2413. [Google Scholar] [CrossRef]
- Altenau, E.H.; Pavelsky, T.M.; Moller, D.; Lion, C.; Pitcher, L.H.; Allen, G.H.; Bates, P.D.; Calmant, S.; Durand, M.; Smith, L.C. AirSWOT Measurements of River Water Surface Elevation and Slope: Tanana River, AK. Geophys. Res. Lett. 2017, 44, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Tuozzolo, S.; Lind, G.; Overstreet, B.; Mangano, J.; Fonstad, M.; Hagemann, M.; Frasson, R.P.M.; Larnier, K.; Garambois, P.A.; Monnier, J.; et al. Estimating River Discharge with Swath Altimetry: A Proof of Concept Using AirSWOT Observations. Geophys. Res. Lett. 2019, 46, 1459–1466. [Google Scholar] [CrossRef]
- Pitcher, L.H.; Pavelsky, T.M.; Smith, L.C.; Moller, D.K.; Altenau, E.H.; Allen, G.H.; Lion, C.; Butman, D.; Cooley, S.W.; Fayne, J.V.; et al. AirSWOT InSAR Mapping of Surface Water Elevations and Hydraulic Gradients Across the Yukon Flats Basin, Alaska. Water Resour. Res. 2019, 55, 937–953. [Google Scholar] [CrossRef]
- Altenau, E.H.; Pavelsky, T.M.; Moller, D.; Pitcher, L.H.; Bates, P.D.; Durand, M.T.; Smith, L.C. Temporal Variations in River Water Surface Elevation and Slope Captured by AirSWOT. Remote Sens. Environ. 2019, 224, 304–316. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Chen, Z.; Jiang, Y.; Fan, L.; Zeng, G. Exploration and Validation of Wave-height Measurement Using Multifrequency HF radar. J. Atmos. Ocean. Technol. 2013, 30, 2189–2202. [Google Scholar]
- Chen, G.; Tang, J.; Zhao, C.; Wu, S.; Yu, F.; Ma, C.; Xu, Y.; Chen, W.; Zhang, Y.; Liu, J.; et al. Concept Design of the "Guanlan" Science Mission: China’s Novel Contribution to Space Oceanography. Front. Mar. Sci. 2019, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Tanelli, S.; Durden, S.L.; Im, E. Simultaneous Measurements of Ku- and Ka-band Sea Surface Cross Sections by an Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 359–363. [Google Scholar] [CrossRef]
- Hossan, A.; Jones, W.L. Ku- and Ka-Band Ocean Surface Radar Backscatter Model Functions at Low-Incidence Angles Using Full-Swath GPM DPR Data. Remote Sens. 2021, 13, 1569. [Google Scholar] [CrossRef]
- Mori, S.; Polverari, F.; Mereu, L.; Pulvirenti, L.; Montopoli, M.; Pierdicca, N.; Marzano, F.S.; IEEE. Atmospheric Precipitation Impact on Synthetic Aperture Radar Imagery: Numerical Model at X and Ka Bands. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Tonboe, R.T.; Nandan, V.; Yackel, J.; Kern, S.; Pedersen, L.T.; Stroeve, J. Simulated Ka- and Ku-band Radar Altimeter Height and Freeboard Estimation on Snow-covered Arctic Sea Ice. Cryosphere 2021, 15, 1811–1822. [Google Scholar] [CrossRef]
- Kong, W.; Chong, J.; Tan, H. Performance Analysis of Ocean Surface Topography Altimetry by Ku-Band Near-Nadir Interferometric SAR. Remote Sens. 2017, 9, 933. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.; Rao, S.; Raju, D.H. Ocean Wave Parameters Estimation Using Backpropagation Neural Networks. Mar. Struct. 2005, 18, 301–318. [Google Scholar] [CrossRef]
- Shao, W.; Li, X.; Sun, J. Ocean Wave Parameters Retrieval from TerraSAR-X Images Validated Against Buoy Measurements and Model Results. Remote Sens. 2015, 7, 12815–12828. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, A.K.; Goldstein, R.M. Crossed orbit interferometry: Theory and experimental results from SIR-B. Int. J. Remote Sens. 1988, 9, 857–872. [Google Scholar] [CrossRef]
- Lin, Q.; Vesecky, J.F. New approaches in interferometric SAR data processing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 560–567. [Google Scholar] [CrossRef]
- Stone, H.S.; Orchard, M.T.; Chang, E.C.; Martucci, S.A. A fast direct Fourier-based algorithm for subpixel registration of images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2235–2243. [Google Scholar] [CrossRef] [Green Version]
- Yague-Martinez, N.; Rossi, C.; Lachaise, M.; Rodriguez-Gonzalez, F.; Fritz, T.; Breit, H. Interferometric processing algorithms of TANDEM-X data. In Proceedings of the 30th IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 June 2010. [Google Scholar]
- Bamler, R. Interferometric stereo radargrammetry: Absolute height determination from ERS-ENVISAT interferograms. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000. [Google Scholar]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing, 2nd ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2016. [Google Scholar]
- Sun, D.; Zhang, Y.; Wang, Y.; Chen, G.; Sun, H.; Yang, L.; Bai, Y.; Yu, F.; Zhao, C. Ocean Wave Inversion Based on Airborne IRA Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 13. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Y.; Zhou, X.; Zhu, L.; Yu, F. Calibration of an Airborne Interferometric Radar Altimeter over the Qingdao Coast Sea, China. Remote Sens. 2020, 12, 1651. [Google Scholar] [CrossRef]
- Rodriguez, E.; Martin, J.M. Theory and Design of Interferometric Synthetic Aperture Radars. IEE Proc. F Radar Signal Process. 1992, 139, 147–159. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherland, 2001. [Google Scholar]
- Zebker, H.A.; Villasenor, J. Decorrelation in Interferometric Radar Echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef] [Green Version]
- Just, D.; Bamler, R. Phase Statistics of Interferograms with Applications to Synthetic Aperture Radar. Appl. Optics. 1994, 33, 4361–4368. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Madsen, S.R.N.; Moghaddam, M.; Van Zyl, J.J. Vegetation Characteristics and Underlying Topography from Interferometric Radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Krieger, G.; Fiedler, H.; Zink, N.; Hajnsek, I.; Younis, M.; Huber, S.; Bachmann, M.; Gonzalez, J.H.; Werner, M.; Moreira, A.; et al. The TanDEM-X mission: A Satellite Formation for High-resolution SAR Interferometry. In Proceedings of the 4th European Radar Conference, Munich, Germany, 10–12 October 2007. [Google Scholar]
- Bai, Y.; Wang, Y.; Zhang, Y.; Zhao, C.; Chen, G. Impact of Ocean Waves on Guanlan’s IRA Measurement Error. Remote Sens. 2020, 12, 1534. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, M.; Zhang, Y.; Wang, C.; Duan, T. An Analytical Method for Dynamic Wave-Related Errors of Interferometric SAR Ocean Altimetry under Multiple Sea States. Remote Sens. 2021, 13, 986. [Google Scholar] [CrossRef]
















| Parameters | Frequency Band | |
|---|---|---|
| Ku-Band | Ka-Band | |
| Center frequency | 15.8 GHz | 35.8 GHz |
| Baseline length | 0.6 m | 0.34 m |
| Incidence angle | 6–18° | 4–17° |
| Bandwidth | 900 MHz | |
| Sample frequency | 1.2 GHz | |
| Antenna operation mode | Single transmission and dual reception | |
| Pulse repetition frequency | 2500 Hz | |
| Flight altitude | 3.38 km | |
| Flight velocity | 68 m/s | |
| Baseline roll angle | 10° | |
| Data | EWD/° | WPD/° | |
|---|---|---|---|
| Main Swell | Main Wind Wave | ||
| Mobile weather station | Southeast | - | - |
| Ku band | - | ~105 | ~80 |
| Ka band | - | ~105 | ~80 |
| Data | SWH/m | Bias/m | MWW/m | |||
|---|---|---|---|---|---|---|
| Swell | Bias/m | Wind Waves | Bias/m | |||
| GNSS buoy | 0.69 | - | 62.83 | - | 22.44 | - |
| Ku band | 1.07 | 0.38 | 46.08 | 16.75 | 20.12 | 2.32 |
| Ka band | 0.96 | 0.27 | 59.16 | 3.67 | 23.01 | 0.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Pan, L.; Qiu, Z.; Liang, D.; Chen, G.; Yu, F.; Sun, H.; Sun, D.; Wu, W. Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter. Remote Sens. 2022, 14, 3578. https://doi.org/10.3390/rs14153578
Ma C, Pan L, Qiu Z, Liang D, Chen G, Yu F, Sun H, Sun D, Wu W. Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter. Remote Sensing. 2022; 14(15):3578. https://doi.org/10.3390/rs14153578
Chicago/Turabian StyleMa, Chunyong, Lichao Pan, Zhiwei Qiu, Da Liang, Ge Chen, Fangjie Yu, Hanwei Sun, Daozhong Sun, and Weifeng Wu. 2022. "Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter" Remote Sensing 14, no. 15: 3578. https://doi.org/10.3390/rs14153578
APA StyleMa, C., Pan, L., Qiu, Z., Liang, D., Chen, G., Yu, F., Sun, H., Sun, D., & Wu, W. (2022). Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter. Remote Sensing, 14(15), 3578. https://doi.org/10.3390/rs14153578