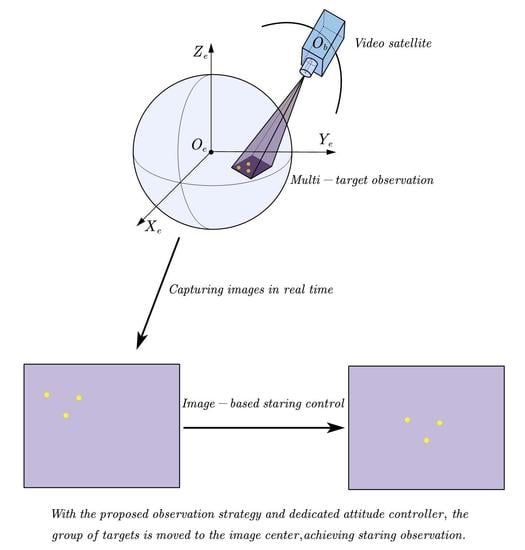
1. Introduction
Conventional remote sensing satellites tend to conduct Earth observation in a push-broom or push-frame manner, while the emerging video satellites are capable of capturing real-time continuous images. To lower the cost and accelerate the development schedule, these video satellites normally adopt the commercial-off-the-shelf (COTS) components and are designed to be miniaturized. Therefore, microsatellites (e.g., Skybox [
1], LAPAN-TUBSAT [
2], Tiantuo-2 [
3] and so on) and CubeSats (e.g., HiREV [
4] and Hera Constellation [
5]) stand out in these video-based Earth observation missions. Using a staring attitude controller, a video satellite can constantly orient the space-borne camera towards the ground targets for a period of time when the satellite flies over the region of interest (ROI). In this way, video satellites are qualified for applications like disaster relief, ground surveillance, and so on. However, there are still challenges remaining unsolved. First, the staring control for a single target has been developed using different methods, but a dedicated controller for the scenario where multiple targets are to be observed has been missing. Second, in the presence of an uncalibrated camera, previous control methods are faced with a decline in pointing accuracy. In this paper, we propose an image-based adaptive staring controller that takes advantage of image information to achieve multi-target observation.
Staring control methods have been primarily based on the prior location information of the target, which we could call a position-based method. Since the ground target is fixed on the Earth’s surface, the location of the target to be observed can be acquired according to its longitude, latitude, and height. Also, the target’s velocity in the inertial frame is computed through Earth rotation. On the basis of the location, ref. [
6] designs the desired attitude in both numerical and analytical ways and then proposes a PD-like staring controller to achieve the desired camera pointing. Ref. [
7] proposes a slide-mode controller using a similar position-based attitude formulation. Ref. [
8] generates staring control commands analytically for Earth observation satellite and compares different position-based staring control methods. It is worth noting that these staring controllers, including other applications in [
9,
10,
11,
12,
13,
14,
15,
16,
17], deal with only a single target, thus are not adequate to properly observe a group of targets when they are in the field of view (FOV) simultaneously.
Compared with a single target observation task, observation for multiple targets is more complex. If the ground targets are distributed sparsely, the camera can capture only one target in one frame. If the targets are distributed densely, they can be seen in the FOV and recorded in one frame simultaneously. For the former observation case, Cui [
18,
19] considers targets located along the sub-satellite track, and adjusts the attitude of the satellite to stare at the ground targets consecutively. The observation is divided into two phases: the stable phase when observing one target and the transition phase when switching to the next target. Two different control methods are proposed. One [
18] is a conventional PD-like controller but with variable coefficients in corresponding phases, and the other one [
19] is an optimal controller that schedules the observation strategy. Similarly, ref. [
20] studies a scheduling problem for aerial targets. Although multiple ground targets are considered in this scenario, the targets are distant from each other, hence only one target appears on the image at one time, and the multi-target observation is essentially transformed into a sequence of single-target observations. For the latter observation case, the way to solve the problem that the image contains more than one target at one time remains unclear, therefore we will propose our solution in this paper.
In practice, the placement and the structure of the camera can differ from the ideal conditions because of the vibration, thermal-induced influence, and other complex factors during the launch and in-orbit operation. Considering such an uncalibrated camera, no matter whether multiple targets are considered, the aforementioned position-based methods cannot avoid the pointing deviation because they are solely dependent on the location information of the target. Thus, an adaptive image-based staring controller is developed to overcome the drawbacks of those position-based methods.
To utilize the image information, the pixel coordinate of a target on the image should be first extracted. In fact, the state-of-art image processing techniques [
21,
22,
23,
24,
25,
26] have been constantly progressing to accomplish the target identification or tracking, and this paper attaches importance to the image-based control instead of image processing, i.e., we do not consider the image processing time. In staring imaging applications, ref. [
27] proposes an image-based control algorithm but the image is only used to designate a vector to align with a ground vector, which is essentially still a position-based method. Ref. [
28] realizes a staring controller whose attitude errors are derived from the image errors. The problem is that the camera in his method is assumed to be fully calibrated, which is quite difficult in reality. Both uncalibrated and calibrated cameras have been widely studied in robotics [
29,
30], UAVs [
31,
32] and many other engineering areas [
33,
34,
35,
36], but the dynamics considered in these works are different from those of a spacecraft, thus are not applicable to staring attitude control.
To sum up, some of the aforementioned studies are fully based on position, some only observe a single target, and some neglect the uncertainties of an uncalibrated camera. This paper deals with the situation where multiple targets appear on the image and the video satellite equipped with an uncalibrated camera is supposed to stare at these targets. First, we propose a selection strategy to designate two targets as representatives, and our controller is based on the two representatives rather than the whole set of targets. Second, we propose an image-based adaptive staring controller using parameter estimation, so that, even though the camera is uncalibrated, we can still accomplish the staring observation.
The paper is organized as follows. In
Section 2, the projection model of a pin-hole camera is established. In
Section 3, the multi-target observation problem is formulated based on the image-based kinematics. In
Section 4, the selection strategy of the targets is introduced, and then we propose the adaptive controller, including the definition and estimation of parameters.
Section 5 gives the simulation samples of the selection strategy and controller respectively. Conclusions are drawn in
Section 6.
3. Problem Formulation
This section first introduces the way to simplify the multi-target observation problem and then establishes the kinematics and dynamics of attitude motion in the form of pixel coordinates. In the end, the problem of a multi-target staring observation is formulated.
3.1. Multi-Target Observation
Assuming all the targets are contained in the FOV at the same time and hence can be detected on the image frame, we propose a strategy to observe the entirety of the targets properly. Like the example, in
Figure 4a, the rectangle denotes the image borders, inside which there are 5 target points. For single-target observation, our staring objective is to control the only target to the image center. For a multi-target case, however, if we only consider a single target, this may lead to an unexpected result. Take
Figure 4b as an example. Point 1 is moved to the image center but point 5 is lost in the FOV. And point 3 and 4 are far from the image center, which is not preferable either.
In light of this, we would prefer all the targets to be similarly distributed around the image center. One possible solution is to move the center of mass to the image center. Without loss of generality, we assume every point owns the same mass weight. Hence, for
n targets whose pixel coordinates are denoted as
,
, the center of mass is given by
The control objective is then to move to the image center. However, a new problem arises in a situation where most target points are densely distributed in a small area while a few other points are far from this area. In this situation, is almost the center of dense points, and our solution will finally place the dense points around the image center, from which the other points will be very far.
To realize the overall more balanced observation, we propose a selection strategy, which first classifies the target group into two clusters and then selects one target from each cluster, i.e., two targets in total. The center of mass will be replaced by the midpoint of these two targets as our control object. In this way, two clusters are equally important and therefore have a similar distance from the image center. The details of this strategy will be further explained later.
3.2. Attitude Kinematics and Dynamics
The satellite in our study is regarded as a rigid body. Assume
is the Euler axis from the ECI to the body frame and
is the rotation angle, then the attitude can be described by a quaternion
, which is defined as
where
is the scalar part and
is the vector part of the quaternion, and the constraint
always holds. Let
be the angular velocity of the satellite with respect to the ECI frame expressed in the body frame, and we have the attitude kinematics given by
where
is the
identity matrix. For any 3-dimensional vector
, the arithmetic operator
is defined as
The attitude dynamics of a rigid satellite are given by
where
J represents the inertia matrix of the satellite and
is the attitude control torques.
3.3. Projection Kinematics for a Single Point
Though the attitude of a satellite can be expressed in the form of a quaternion, instead of using an error quaternion like a conventional position-based method, our image-based method uses the error of the pixel coordinates to represent attitude error. Therefore, we need to figure out how the pixel coordinate varies with the angular velocity. Differentiate the depth
from Equation (
10) and we get
where
is the velocity of the ground target and
is the velocity of the satellite. Similarly, the derivative of the image coordinate is given by
For simplicity, we define the matrix
Then Equations (
16) and (
17) can be rewritten as
3.4. Projection Kinematics for Multiple Points
As we select two targets as the representatives of the entire group of targets, the kinematics of double target points should be derived. The center of mass of two targets is also their midpoint, which is
where
and
are the two points respectively. The corner mark
and
are used to represent the two selected points in the remainder of this paper. Then we have
where
Equations (
21) and (
22) are the dynamics of the midpoint of two targets. The way to select the two targets will be introduced in the next section.
3.5. Control Objective
At the initial time, a couple of ground targets are detected on the image through the space-borne camera. To acquire a better view of the entirety of the targets, we expect the center of mass of the target group to be located at the image center. In pursuit of a balanced observation, the midpoint of two targets are picked out to best represent the group’s center of mass according to our proposed selection strategy. With a proper estimation of the camera-related parameters, our objective of the proposed adaptive controller is to move to the image center, which is denoted as .
4. Controller Design
In this section, the selection strategy is firstly introduced to find the two most suitable targets, which will then be used by the controller to achieve the control objective. As the camera is uncalibrated, the elements of the projection matrix N are unknown, hence the parameters to be estimated should be defined. Due to the fact that the ground point is constantly moving along with the Earth’s rotation, it is rather tough to determine the desired angular velocity when the target projection has reached . Thus, a reference attitude trajectory will be proposed to avoid designing desired angular velocity in this section. And the adaptive staring controller will be designed based on the estimated parameters and the reference attitude.
4.1. Target-Selection Strategy Using a Clustering Method
Assuming there are targets denoted as , on the image, we propose the following strategy to select two points to best serve our multi-target observation.
Step 1: We adopt a clustering algorithm, i.e., k-means [
37], to classify all the targets into two clusters, e.g.,
and
. As a result, every point is classified as one of the two clusters and has the least distance from the center of mass of its corresponding cluster. Denote
and
as the center of mass of
and
respectively, then for any
, we have
For any
, we have
Step 2: We walk through all the target pairs consisting of two targets from the two clusters respectively. The target pair, of which the center of mass is closest to the center of mass of all the targets, is selected. Denote the selected targets as
and
, and they satisfy
Step 1 is to guarantee the balance of observation emphasis between two clusters, and step 2 is to find two proper targets whose midpoint resembles the center of mass of the entire target group most. Based on two selected targets, the following adaptive controller is designed to achieve the staring observation for multiple targets.
4.2. Parameter Definition
Due to the uncertainties of the uncalibrated camera, we have to properly define the camera parameters so that we can linearize and then estimate these parameters online. The parameter linearization is the basis of the parameter estimation and therefore we can formulate the adaptive controller using these estimated parameters. According to Equations (
10) and (
20), we have
Each element of the projection matrix
N appearing in the above equation is coupled with another element, i.e., they appear in the form of a product of two elements. We define these coupling products as the parameters
to be estimated. More specifically, after Equation (
27) is expanded, we can find that
consists of the products of
times every element of
N, every element of
times every element of
and every element of
times every element of
. Hence
contains 42 parameters. As we can infer, the number of the parameters defined will fast increase when dealing with the center of mass of over two targets. In other words, the parameter estimation process will be more complex and computationally demanding. Therefore, our target-selection strategy is also able to reduce the computational burden.
The estimated values of the parameters are denoted as , and the head mark is used to represent the estimated variables in the remainder of this paper.
4.3. Reference Attitude Trajectory
A PD-like controller requires the convergence of both the image error
and the angular velocity error
. But the time-varying desired angular velocity
is hard to directly design. To avoid using
, we propose the reference attitude. In this way, the attitude of the satellite is controlled to track the reference attitude instead. Define a reference trajectory of the midpoint as
:
The reference angular velocity trajectory
is defined as
where the pseudo inverse matrix
of
is defined as
and reflect the tracking error between the current attitude and the reference attitude. Worth noting that, the convergence of infers the convergence of , which, according to its definition, is mathematically obvious and hence no proof is listed here.
4.4. Parameter Estimation
The estimation error is defined as
. According to Equation (
27), an estimated projection error
used to measure the performance of the parameter estimation is given by
The matrix
does not contain any camera parameters. Due to the proper definition of parameters,
is linear with respect to
, which enables us to estimate the parameters. Accordingly, we propose an updating law for the parameters
:
where the regressor matrix
is given by
and
are the diagonal positive coefficient matrices, and
does not contain any camera parameters. The updating law (
32) contains two main parts. The first part will be utilized in the stability proof, and the second is about the negative gradient of
, which updates the parameters in a direction that
is reducing.
4.5. Adaptive Staring Controller
The adaptive staring controller is given by
where
is the attitude control torque,
and
are the diagonal positive coefficient matrices. Define two non-negative function
Then we have the Lyapunov function
. Differentiate
:
We rewrite
and
:
The
part in Equation (
36) can then be rewritten as
Substitute Equations (
38)–(
40) into (
36) and (
37), and the following inequality is obtained
We can conclude that
,
and
are all bounded, which leads to the control torque
also being bounded. According to the dynamics Equation (
15),
is bounded. Considering the expression of
and
, they are bounded, too. Therefore, we have the boundedness of
. According to Barbalat’s Lemma, the following convergence is obtained
which suggests that
Hence the stability of the proposed adaptive staring controller is proved. The midpoint of two ground targets’ projections on the image plane is moved to the image center under the effect of our controller.
6. Conclusions
In light of the lack of a staring control method for a multi-target observation scenario, especially for an uncalibrated camera of a miniaturized video satellite, we propose an image-based adaptive staring controller. First, a selection strategy based on a clustering method is proposed and two targets as representatives are picked out of the entirety of the targets, which realizes a more balanced overall observation and also reduces the computational complexity. Second, the unknown camera parameters are estimated according to the self-updating law. As a result, the estimated projection error decreases. Third, the image-based adaptive staring controller for multiple targets is established using the estimated parameters. The simulations demonstrate the effectiveness of our proposed method. In the test case, though the camera is uncalibrated, our controller accomplishes the staring observation for a group of targets on the image.
In this paper, the motion of ground targets is predictable due to Earth’s rotation. For targets with unpredictable motion, a dedicated staring controller remains to be developed in the future.