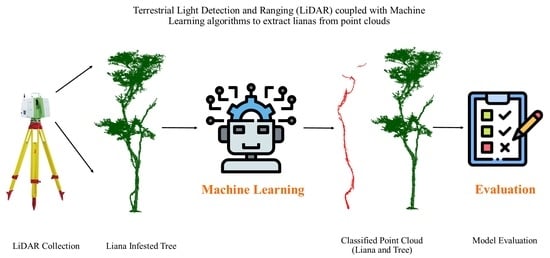
Extraction of Liana Stems Using Geometric Features from Terrestrial Laser Scanning Point Clouds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Data Processing
2.2.1. Predictor Variables
2.2.2. Data Labelling
2.2.3. Optimum Radius for Near-Neighbor Search
2.2.4. Classification
2.2.5. Performance Assessment
2.3. Intercomparison with the Existing Method
3. Results
3.1. Geometric Features Analysis
3.2. Model Performance
3.3. Intercomparison
4. Discussion
4.1. Geometric Feature Analysis
4.2. Liana-Tree Classification
4.3. Intercomparison with the Literature Method
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ingwell, L.L.; Joseph Wright, S.; Becklund, K.K.; Hubbell, S.P.; Schnitzer, S.A. The Impact of Lianas on 10 Years of Tree Growth and Mortality on Barro Colorado Island, Panama. J. Ecol. 2010, 98, 879–887. [Google Scholar] [CrossRef]
- Letcher, S.G.; Chazdon, R.L. Lianas and Self-Supporting Plants during Tropical Forest Succession. For. Ecol. Manag. 2009, 257, 2150–2156. [Google Scholar] [CrossRef]
- Durán, S.M.; Gianoli, E. Carbon Stocks in Tropical Forests Decrease with Liana Density. Biol. Lett. 2013, 9, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Ronderos, M.E.; Bohrer, G.; Sanchez-Azofeifa, A.; Powers, J.S.; Schnitzer, S.A. Contribution of Lianas to Plant Area Index and Canopy Structure in a Panamanian Forest. Ecology 2016, 97, 3271–3277. [Google Scholar] [CrossRef]
- Schnitzer, S.A. A Mechanistic Explanation for Global Patterns of Liana Abundance and Distribution. Am. Nat. 2005, 166, 262–276. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, G.A.; Castro-Esau, K. Canopy Observations on the Hyperspectral Properties of a Community of Tropical Dry Forest Lianas and Their Host Trees. Int. J. Remote Sens. 2006, 27, 2101–2109. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; Estrada-Villegas, S.; Wright, S.J. The Response of Lianas to 20 Yr of Nutrient Addition in a Panamanian Forest. Ecology 2020, 101, e03190. [Google Scholar] [CrossRef]
- Wright, S.J. Tropical Forests in a Changing Environment. Trends Ecol. Evol. 2005, 20, 553–560. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, G.A.; Guzmán-Quesada, J.A.; Vega-Araya, M.; Campos-Vargas, C.; Durán, S.M.; D’Souza, N.; Gianoli, T.; Portillo-Quintero, C.; Sharp, I. Can Terrestrial Laser Scanners (TLSs) and Hemispherical Photographs Predict Tropical Dry Forest Succession with Liana Abundance? Biogeosciences 2017, 14, 977–988. [Google Scholar] [CrossRef]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S.; et al. Estimation of Above-Ground Biomass of Large Tropical Trees with Terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; Bongers, F. Increasing Liana Abundance and Biomass in Tropical Forests: Emerging Patterns and Putative Mechanisms. Ecol. Lett. 2011, 14, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Schnitzer, S.A.; Bongers, F. The Ecology of Lianas and Their Role in Forests. Trends Ecol. Evol. 2002, 17, 223–230. [Google Scholar] [CrossRef]
- Gentry, A.H. The Distribution and Evolution of Climbing Plants. In The Biology of Vines; Cambridge University Press: Cambridge, UK, 1992; pp. 3–50. [Google Scholar]
- Schnitzer, S.A. Testing Ecological Theory with Lianas. New Phytol. 2018, 220, 366–380. [Google Scholar] [CrossRef] [PubMed]
- Dewalt, S.J.; Schnitzer, S.A.; Denslow, J.S. Density and Diversity of Lianas along a Chronosequence in a Central Panamanian Lowland Forest. J. Trop. Ecol. 2000, 16, 1–19. [Google Scholar] [CrossRef]
- Moorthy, S.M.; Bao, Y.; Calders, K.; Schnitzer, S.A.; Verbeeck, H. Semi-Automatic Extraction of Liana Stems from Terrestrial LiDAR Point Clouds of Tropical Rainforests. ISPRS J. Photogramm. Remote Sens. 2019, 154, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Moorthy, S.M.; Calders, K.; di Porcia e Brugnera, M.; Schnitzer, S.; Verbeeck, H. Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure. Remote Sens. 2018, 10, 810. [Google Scholar] [CrossRef]
- Londré, R.A.; Schnitzer, S.A. The Distribution of Lianas and Their Change in Abundance in Temperate Forests over the Past 45 Years. Ecology 2006, 87, 2973–2978. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive Estimates of Above-Ground Biomass Using Terrestrial Laser Scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Bao, Y.; Moorthy, S.; Verbeeck, H. Towards Extraction of Lianas from Terrestrial Lidar Scans of Tropical Forests. Int. Geosci. Remote Sens. Symp. 2018, 2018, 7544–7547. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.L.; Fournier, R.A.; Verstraete, M.M. On Seeing the Wood from the Leaves and the Role of Voxel Size in Determining Leaf Area Distribution of Forests with Terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A.; Côté, J.F.; Verstraete, M.M. Estimating Leaf Area Distribution in Savanna Trees from Terrestrial LiDAR Measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Tao, S.; Guo, Q.; Xu, S.; Su, Y.; Li, Y.; Wu, F. A Geometric Method for Wood-Leaf Separation Using Terrestrial and Simulated Lidar Data. Photogramm. Eng. Remote Sens. 2015, 81, 767–776. [Google Scholar] [CrossRef]
- Moorthy, S.M.; Calders, K.; Vicari, M.B.; Verbeeck, H. Improved Supervised Learning-Based Approach for Leaf and Wood Classification from LiDAR Point Clouds of Forests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3057–3070. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and Wood Classification Framework for Terrestrial LiDAR Point Clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Niemann, K.O.; Liu, J.; Shi, Y.; Wang, T. Foliar and Woody Materials Discriminated Using Terrestrial LiDAR in a Mixed Natural Forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 43–50. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, G.; Eitel, J.U.H.; Moskal, L.M.; He, W.; Huang, H. Improved Salient Feature-Based Approach for Automatically Separating Photosynthetic and Nonphotosynthetic Components Within Terrestrial Lidar Point Cloud Data of Forest Canopies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 679–696. [Google Scholar] [CrossRef]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3D lidar point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-5/W12, 97–102. [Google Scholar] [CrossRef]
- Thomas, H.; Goulette, F.; Deschaud, J.-E.; Marcotegui, B.; LeGall, Y. Semantic Classification of 3D Point Clouds with Multiscale Spherical Neighborhoods. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; IEEE: Piscataway, NJ, USA; pp. 390–398. [Google Scholar]
- Belton, D.; Moncrieff, S.; Chapman, J. Processing Tree Point Clouds Using Gaussian Mixture Models. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 43–48. [Google Scholar] [CrossRef]
- Koenig, K.; Höfle, B.; Hämmerle, M.; Jarmer, T.; Siegmann, B.; Lilienthal, H. Comparative Classification Analysis of Post-Harvest Growth Detection from Terrestrial LiDAR Point Clouds in Precision Agriculture. ISPRS J. Photogramm. Remote Sens. 2015, 104, 112–125. [Google Scholar] [CrossRef]
- Wang, D.; Brunner, J.; Ma, Z.; Lu, H.; Hollaus, M.; Pang, Y.; Pfeifer, N. Separating Tree Photosynthetic and Non-Photosynthetic Components from Point Cloud Data Using Dynamic Segment Merging. Forests 2018, 9, 252. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, G.A.; Kalácska, M.; do Espírito-Santo, M.M.; Fernandes, G.W.; Schnitzer, S. Tropical Dry Forest Succession and the Contribution of Lianas to Wood Area Index (WAI). For. Ecol. Manag. 2009, 258, 941–948. [Google Scholar] [CrossRef]
- Guzmán, Q.J.A.; Rivard, B.; Sánchez-Azofeifa, G.A. Discrimination of Liana and Tree Leaves from a Neotropical Dry Forest Using Visible-near Infrared and Longwave Infrared Reflectance Spectra. Remote Sens. Environ. 2018, 219, 135–144. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D. Assessing Mangrove Above-Ground Biomass and Structure Using Terrestrial Laser Scanning: A Case Study in the Everglades National Park. Wetlands 2014, 34, 955–968. [Google Scholar] [CrossRef]
- Taheriazad, L.; Moghadas, H.; Sanchez-Azofeifa, A. Calculation of Leaf Area Index in a Canadian Boreal Forest Using Adaptive Voxelization and Terrestrial LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101923. [Google Scholar] [CrossRef]
- Côté, J.F.; Fournier, R.A.; Frazer, G.W.; Olaf Niemann, K. A Fine-Scale Architectural Model of Trees to Enhance LiDAR-Derived Measurements of Forest Canopy Structure. Agric. For. Meteorol. 2012, 166, 72–85. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual Tree Biomass Estimation Using Terrestrial Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; DeWalt, S.J.; Chave, J. Censusing and Measuring Lianas: A Quantitative Comparison of the Common Methods. Biotropica 2006, 38, 581–591. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D Structure and Occlusion in Dense Tropical and Temperate Forests Using Close-Range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Weinmann, M.; Urban, S.; Hinz, S.; Jutzi, B.; Mallet, C. Distinctive 2D and 3D Features for Automated Large-Scale Scene Analysis in Urban Areas. Comput. Graph. 2015, 49, 47–57. [Google Scholar] [CrossRef]
- Wang, D.; Hollaus, M.; Pfeifer, N. Feasibility of Machine Learning Methods for Separating Wood and Leaf Points from Terrestrial Laser Scanning Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 157–164. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, G.; Eitel, J.U.H.; Magney, T.S.; Moskal, L.M. Determining Woody-to-Total Area Ratio Using Terrestrial Laser Scanning (TLS). Agric. For. Meteorol. 2016, 228, 217–228. [Google Scholar] [CrossRef]
- Calvo-Rodriguez, S.; Kiese, R.; Sánchez-Azofeifa, G.A. Seasonality and Budgets of Soil Greenhouse Gas Emissions From a Tropical Dry Forest Successional Gradient in Costa Rica. J. Geophys. Res. Biogeosci. 2020, 125, e2020JG005647. [Google Scholar] [CrossRef]
- Burt, A.; Disney, M.; Calders, K. Extracting Individual Trees from Lidar Point Clouds Using Treeseg. Methods Ecol. Evol. 2019, 10, 438–445. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Project 2021. Available online: http://www.R-project.org/ (accessed on 18 July 2022).
- Rhys, H.I. Machine Learning with R, the Tidyverse, and Mlr; Manning: Shelter Island, NY, USA, 2020; ISBN 9781617296574. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; ACM: New York, NY, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Lakicevic, M.; Povak, N.; Reynolds, K.M. Introduction to R for Terrestrial Ecology; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-27602-7. [Google Scholar]
- Tao, S.; Wu, F.; Guo, Q.; Wang, Y.; Li, W.; Xue, B.; Hu, X.; Li, P.; Tian, D.; Li, C.; et al. Segmenting Tree Crowns from Terrestrial and Mobile LiDAR Data by Exploring Ecological Theories. ISPRS J. Photogramm. Remote Sens. 2015, 110, 66–76. [Google Scholar] [CrossRef]
- Ferrara, R.; Virdis, S.G.P.; Ventura, A.; Ghisu, T.; Duce, P.; Pellizzaro, G. An Automated Approach for Wood-Leaf Separation from Terrestrial LIDAR Point Clouds Using the Density Based Clustering Algorithm DBSCAN. Agric. For. Meteorol. 2018, 262, 434–444. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]







| Tree ID | Tree Stem | DBH (cm) | Height (m) | Liana Infestation Levels | Liana Points Proportion | Number of Total Points |
|---|---|---|---|---|---|---|
| Tree 1 | 1 | 54.10 | 16.49 | Low | 1% | 405,262 |
| Tree 2 | 1 | 30.70 | 14.51 | Low | 4% | 121,954 |
| Tree 3 | 1 | 28.90/31.20/38.40 * | 16.57 | High | 9% | 382,599 |
| Tree 4 | 1 | 55 | 17.10 | High | 15% | 622,967 |
| Tree 5 | 1 | 20.50 | 13.96 | Intermediate | 37% | 87,346 |
| No. | Feature | Description |
|---|---|---|
| 1 | Omnivariance | 3√) |
| 2 | Anisotropy | |
| 3 | Planarity | |
| 4 | Linearity | |
| 5 | Sphericity | |
| 6 | Verticality |
| Feature | Tree ID | |||||
|---|---|---|---|---|---|---|
| Tree 1 | Tree 2 | Tree 3 | Tree 4 | Tree 5 | Independent | |
| Omnivariance | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Anisotropy | 1.00 | 0.86 | 0.98 | 0.50 | 0.45 | 0.37 |
| Planarity | 0.13 | 0.99 | 0.22 | 0.16 | 0.87 | 0.29 |
| Linearity | 0.18 | 0.91 | 1.00 | 0.40 | 0.21 | 0.33 |
| Sphericity | 1.00 | 0.73 | 1.00 | 0.51 | 0.21 | 0.37 |
| Verticality | 1.00 | 0.68 | 0.24 | 1.00 | 0.70 | 0.45 |
| Tree ID | Random Forest | XGBoosting | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Precision | Recall | F1 Score | Accuracy | Aa | Precision | Recall | F1 Score | Accuracy | Aa | |
| Tree 1 | 0.05 | 0.44 | 0.09 | 0.9 | 0.09 | 0.12 | 0.47 | 0.19 | 0.95 | 0.51 |
| Tree 2 | 0.2 | 0.72 | 0.31 | 0.88 | 0.35 | 0.29 | 0.77 | 0.42 | 0.9 | 0.86 |
| Tree 3 | 0.32 | 0.37 | 0.34 | 0.82 | 0.21 | 0.3 | 0.44 | 0.36 | 0.85 | 0.5 |
| Tree 4 | 0.68 | 0.74 | 0.71 | 0.91 | 0.73 | 0.7 | 0.8 | 0.75 | 0.91 | 0.86 |
| Tree 5 | 0.67 | 0.52 | 0.59 | 0.73 | 0.69 | 0.65 | 0.82 | 0.73 | 0.77 | 0.89 |
| Ave | 0.38 | 0.56 | 0.41 | 0.85 | 0.41 | 0.41 | 0.66 | 0.49 | 0.88 | 0.72 |
| Sd | 0.28 | 0.17 | 0.24 | 0.07 | 0.29 | 0.25 | 0.19 | 0.24 | 0.07 | 0.2 |
| Tree ID | Without Postprocessing | Postprocessing | ||||||
|---|---|---|---|---|---|---|---|---|
| Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | Accuracy | |
| Tree 1 | 0.05 | 0.24 | 0.08 | 0.92 | 0.27 | 0.40 | 0.32 | 0.98 |
| Tree 2 | 0.10 | 0.06 | 0.08 | 0.94 | 0.12 | 0.46 | 0.19 | 0.85 |
| Tree 3 | 0.11 | 0.22 | 0.14 | 0.76 | 0.38 | 0.66 | 0.48 | 0.87 |
| Tree 4 | 0.64 | 0.37 | 0.47 | 0.87 | 0.76 | 0.76 | 0.76 | 0.92 |
| Tree 5 | 0.73 | 0.08 | 0.16 | 0.65 | 0.85 | 0.52 | 0.64 | 0.79 |
| Ave | 0.33 | 0.19 | 0.19 | 0.83 | 0.48 | 0.56 | 0.48 | 0.88 |
| Sd | 0.33 | 0.13 | 0.16 | 0.12 | 0.32 | 0.15 | 0.23 | 0.07 |
| Methods | Model Recall |
|---|---|
| Random Forest | 0.88 |
| Postprocessing | 0.87 |
| XGBoosting | 0.82 |
| Without postprocessing | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Sánchez-Azofeifa, G.A. Extraction of Liana Stems Using Geometric Features from Terrestrial Laser Scanning Point Clouds. Remote Sens. 2022, 14, 4039. https://doi.org/10.3390/rs14164039
Han T, Sánchez-Azofeifa GA. Extraction of Liana Stems Using Geometric Features from Terrestrial Laser Scanning Point Clouds. Remote Sensing. 2022; 14(16):4039. https://doi.org/10.3390/rs14164039
Chicago/Turabian StyleHan, Tao, and Gerardo Arturo Sánchez-Azofeifa. 2022. "Extraction of Liana Stems Using Geometric Features from Terrestrial Laser Scanning Point Clouds" Remote Sensing 14, no. 16: 4039. https://doi.org/10.3390/rs14164039
APA StyleHan, T., & Sánchez-Azofeifa, G. A. (2022). Extraction of Liana Stems Using Geometric Features from Terrestrial Laser Scanning Point Clouds. Remote Sensing, 14(16), 4039. https://doi.org/10.3390/rs14164039