An Improved Coastal Marine Gravity Field Based on the Mean Sea Surface Height Constraint Factor Method
Abstract
:1. Introduction
2. Materials and Methods
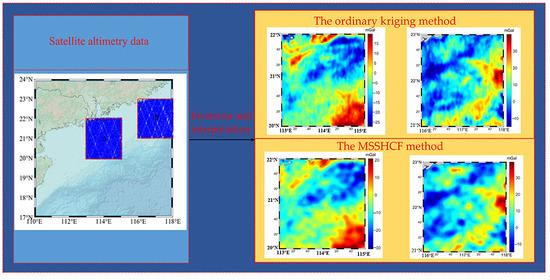
2.1. The Mean Sea Surface Height Constraints Factor (MSSHCF) Method
2.2. Data Preparation and Pre-Processing
2.3. Dynamic Sea Surface Topography, Mean Sea Surface and Reference Gravity Field Model
2.4. The Gravity Data Source for Comparative Verification
3. Results
4. Discussion
4.1. Verification from Coastal Gravity Field Models
4.2. Effect of Sea Depth on Coastal Gravity Field
4.3. Verification against NGDC Shipboard Gravity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Forsberg, R.; Olesen, A.V. Airborne Gravity Field Determination. In Sciences of Geodesy–I; Xu, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 83–104. [Google Scholar]
- Claessens, S.J. Evaluation of gravity and altimetry data in Australian coastal regions. In Geodesy for Planet Earth; Kenyon, S., Pacino, C., Marti, U., Eds.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2012; Volume 136, pp. 435–442. [Google Scholar]
- Barzaghi, R.; Borghi, A.; Keller, K.; Forsberg, R.; Giori, I.; Loretti, I.; Olesen, A.V.; Stenseng, L. Airborne gravity tests in the Italian area to improve the geoid model of Italy. Geophys. Pros. 2009, 57, 625–632. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.V.; Alshamsi, A.; Gidskehaug, A.; Ses, S.; Kadir, M.; Peter, B. Airborne gravimetry survey for the marine area of the United Arab Emirates. Mar. Geod. 2012, 35, 221–232. [Google Scholar] [CrossRef]
- Wu, Y.; Abulaitijiang, A.; Featherstone, W.E.; McCubbine, J.C.; Andersen, O.B. Coastal gravity field refinement by combining airborne and ground-based data. J. Geod. 2019, 93, 2569–2584. [Google Scholar] [CrossRef]
- Lu, B.; Barthelmes, F.; Li, M.; Förste, C.; Ince, E.S.; Petrovic, S.; Flechtner, F.; Schwabe, J.; Luo, Z.; Zhong, B.; et al. Shipborne gravimetry in the Baltic Sea: Data processing strategies, crucial findings and preliminary geoid determination tests. J. Geod. 2019, 93, 1059–1071. [Google Scholar] [CrossRef]
- Rapp, R.H. Gravity Anomalies and Sea Surface Heights Derived from a Combined GEOS 3/Seasat Altimeter Data Set. J. Geophys. Res. 1986, 91, 4867–4876. [Google Scholar] [CrossRef]
- Sandwell, D.; McAdoo, C. Marine gravity of the Southern Ocean and Antartic margin from Geosat. J. Geophys. Res. 1988, 93, 10389–10396. [Google Scholar] [CrossRef]
- Sandwell, D. Antarctic marine gravity field from high-density satellite altimetry. Geophys. J. Int. 1992, 109, 437–448. [Google Scholar]
- Hwang, C.; Parsons, B. An Optimal Procedure for Deriving Marine Gravity from Multi-Satellite Altimetry. Geophys. J. R. Astron. Soc. 1996, 125, 705–718. [Google Scholar] [CrossRef] [Green Version]
- Hwang, C.; Kao, E.; Barry, P. Global derivation of marine gravity anomalies from Marinesat, Geosat, ERS-1 and TOPEX/POSEIDON altimeter data. Geophys. J. Int. 1998, 134, 449–459. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.B.; Knudsen, P. Global Marine Gravity Field from the ERS-1 and Geosat Geodetic Mission Altimetry. J. Geophys. Res. 1998, 103, 8129–8137. [Google Scholar] [CrossRef]
- Garcia, E.S.; Sandwell, D.; Smith, H.F. Retracking CryoSat-2, Envisat and Jason-1 radar altimetry waveforms for improved gravity field recovery. Geophys. J. Int. 2014, 196, 1402–1422. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Liu, X.; Guo, J.; Zhu, C.; Yuan, J.; Gao, J.; Gao, Y.; Ji, B. Performance of Jason-2/GM altimeter in deriving marine gravity with the waveform derivative retracking method: A case study in the South China Marine. Arab. J. Geosci. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Guo, J.; Hwang, C.; Deng, X. Editorial: Application of Satellite Altimetry in Marine Geodesy and Geophysics. Front. Earth Sci. 2022, 10, 910562. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Garcia, E.S.; Soofi, K.; Wessel, P. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1. Lead. Edge 2013, 32, 892–899. [Google Scholar] [CrossRef] [Green Version]
- Che, D.; Li, H.; Zhang, S.; Ma, B. Calculation of Deflection of Vertical and Gravity Anomalies Over the South China Marine Derived from ICESat-2 Data. Front. Earth Sci. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.; Deng, X.; Hsu, H.-Y.; Liu, Y. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data. J. Geod. 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P.; Berry, P. The DNSC08GRA global marine gravity field from double retracked satellite altimetry. J. Geod. 2010, 84, 191–199. [Google Scholar] [CrossRef]
- Passaro, M.; Kildegaard, R.; Andersen, O.B.; Boergens, E.; Calafat, F.M.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous marine retracker for satellite altimetry to marine ice leads, coastal and inland waters. Remote Sens. Environ. 2018, 211, 456–471. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Guo, J.; Gao, J.; Liu, X.; Hwang, C.; Yu, S.; Yuan, J.; Ji, B.; Guan, B. Marine gravity determined from multi-satellite GM/ERM altimeter data over the South China Marine: SCSGA V1.0. J. Geod. 2020, 94, 50. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. The DTU17 global marine gravity field: First validation results. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Sandwell, D.; Smith, H.F. Global marine gravity from retracked Geosat and ERS-1 altimetry: Ridge segmentation versus spreading rate. J. Geophys. Res. 2009, 114, B01411. [Google Scholar] [CrossRef] [Green Version]
- Tseng, K.H.; Shum, C.K.; Yi, Y.; Emery, W.J.; Kuo, C.Y.; Lee, H.; Wang, H. The Improved Retrieval of Coastal Marine Surface Heights by Retracking Modified Radar Altimetry Waveforms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 991–1001. [Google Scholar] [CrossRef]
- Wen, H.; Jin, T.; Zhu, G.; Cheng, P. Principle and Application of Satellite Altimetry; Surveying and Mapping Press: Beijing, China, 2017; pp. 1–199. [Google Scholar]
- Nicolas, F.; Frédéric, M.; Michel, K. 3-Processing Geophysical Maps. Magn. Electron. 2018, 129–148. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, K.; Jiang, M.; Wang, J. Preliminary marine gravity field from HY-2A/GM altimeter data. Acta Oceanol. Sin. 2020, 39, 127–134. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, M.; Han, X.; Zheng, Z.; Zhai, H. Remarinerch on the applicability of Kriging method in regional gravity field interpolation. Eng. Survey Map. 2018, 27, 1–6. [Google Scholar]
- Li, S.; An, Z. Application of Kriging Model in Gravity Data Interpolation. Bull. Surv. Map. 2013, 10, 63–66. [Google Scholar]
- Kamguia, J.; Tabod, C.T.; Tadjou, J.M.; Manguelle, E.; Nouayou, R.; Kande, L.H. Accurate gravity anomaly interpolation: A case-study in Cameroon, Central Africa. Int. J. Earth Sci. 2007, 2, 108–116. [Google Scholar]
- Xu, Y.; Fang, Z.; Cao, W.; Huang, S.; Hao, T. Gravity anomaly reconstruction based on nonequispaced Fourier transform. Geophysics 2019, 84, G83–G92. [Google Scholar] [CrossRef]
- Zhang, W.; Zheng, W.; Li, Z.; Li, K.; Zhang, H. Improving the Reconstruction Accuracy of Marine Gravity Anomaly Encrypted Reference Map Using the New Mean Marine Surface 3-D Correction Method. IEEE Access 2020, 8, 214756–214774. [Google Scholar] [CrossRef]
- Deng, Y.; Gu, S. Spatial distribution characteristics of multipath error based on Kriging interpolation method. Sci. Survey Map. 2018, 43, 17–23. [Google Scholar]
- Mitchell, R.; Porth, C.B.; Porth, L.; Milton, B.; Katerina, R. Improving agricultural microinsurance by applying universal kriging and generalised additive models for interpolation of mean daily temperature. Geneva Pap. Risk Insur. Issues Pract. 2019, 44, 446–480. [Google Scholar]
- Ruehaak, W. 3-D interpolation of subsurface temperature data with measurement error using kriging. Environ. Earth Sci. 2015, 73, 1893–1900. [Google Scholar] [CrossRef]
- Nicolas, H. Defining mean sea level in military simulations with DTED. In Proceedings of the 2009 Spring Simulation Multiconference, SpringSim 2009, San Diego, CA, USA, 22–27 March 2009; Volume 115, pp. 1–3. [Google Scholar]
- Huang, L.; Zhang, H.; Xu, P.; Geng, J.; Wang, C.; Liu, J. Kriging with Unknown Variance Components for Regional Ionospheric Reconstruction. Sensors 2017, 17, 468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, C. Inverse Vening Meinesz formula and deflection geoid formula: Application to prediction of gravity and geoid over the South China Sea. J. Geod. 1998, 72, 304–312. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P.; Stenseng, L. A New DTU18 MSS Mean Sea Surface–Improvement from SAR Altimetry. In Proceedings of the 25 Years of Progress in Radar Altimetry Symposium, Ponta Delgada, Portugal, 24–29 September 2018. [Google Scholar]
- Pavlis, N.; Holmes, S.; Kenyon, S.; Factor, J. The development and evaluation of the Earth Gravitational Model 2008(EGM2008). J. Geophys. Res. 2012, 117, B04406. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Bao, L.; Wang, Y. Accuracy Evaluation of Altimeter-Derived Gravity Field Models in Offshore and Coastal Regions of China. Front. Earth Sci. 2021, 9, 722019. [Google Scholar] [CrossRef]












| Correction | Modification Model or Method |
|---|---|
| Reprocessed method | ALES |
| Dry troposphere correction | European Center for Medium Range Weather Forecasting |
| Wet troposphere correction | European Center for Medium Range Weather Forecasting |
| Ionospheric correction | CNES |
| Marine state bias | CNES |
| Derived barometer height correction | European Center for Medium Range Weather Forecasting |
| High frequency fluctuations of the sea surface topography | LEGOS/CLS/CNES |
| Marine tide | LEGOS/CNES |
| Load tide | GOT4.10 |
| Pole tide | Aviso |
| Region | Method | Model | Max | Min | Mean | Std |
|---|---|---|---|---|---|---|
| A | The ordinary kriging interpolation method VS | SS | 28.32 | −20.2 | −0.83 | 3.25 |
| DTU | 9.68 | −7.15 | −0.45 | 2.01 | ||
| DR | 43.24 | −33.74 | −1.27 | 9.3 | ||
| EGM2008 | 9.25 | −5.58 | −0.35 | 1.79 | ||
| SS | 28.61 | −19.36 | −0.66 | 2.78 | ||
| The MSSHCF method VS | DTU | 8.34 | −5.65 | 0.28 | 1.48 | |
| DR | 36.13 | −33.87 | −1.09 | 8.78 | ||
| EGM2008 | 7.88 | −6.37 | −0.18 | 1.29 | ||
| SS | 15.53 | −13.48 | 0.383 | 3.86 | ||
| B | The ordinary kriging interpolation method VS | DTU | 12.73 | −12.43 | −0.41 | 2.44 |
| DR | 61.04 | −41.21 | 0.8 | 9.9 | ||
| EGM2008 | 10.29 | −12.45 | 0.28 | 1.9 | ||
| SS | 14.58 | −11.44 | 0.3 | 3.5 | ||
| The MSSHCF method VS | DTU | 9.5 | −6.41 | 0.33 | 2.04 | |
| DR | 58.74 | −34.45 | 0.72 | 9.44 | ||
| EGM2008 | 7.79 | −5.83 | 0.2 | 1.44 |
| Distance/km | Model Comparison Results | Max | Min | Mean | Std |
|---|---|---|---|---|---|
| The ordinary kriging | 4.07 | −9.02 | −1.52 | 2.59 | |
| The MSSHCF VS DTU17 | 3.72 | −7.51 | −1.03 | 1.92 | |
| 0~20 | The ordinary kriging | 3.8 | −8.06 | −2.03 | 2.46 |
| The MSSHCF VS EGM2008 | 4.55 | −7.88 | −1.53 | 1.99 | |
| The ordinary kriging | 15.84 | −33.89 | −13.93 | 9.97 | |
| The MSSHCF VS DR | 13.98 | −33.57 | −13.44 | 9.47 | |
| The ordinary kriging | 18.9 | −26.38 | −0.19 | 6.45 | |
| The MSSHCF VS SS V28 | 18.22 | −26.25 | 0.3 | 5.71 | |
| The ordinary kriging | 6.3 | −5.64 | 0.9 | 2.13 | |
| The MSSHCF VS DTU17 | 4.09 | −4.92 | 0.57 | 1.58 | |
| 20~50 | The ordinary kriging | 4.77 | −7.34 | 0.58 | 1.83 |
| The MSSHCF VS EGM2008 | 3.53 | −4.96 | 0.31 | 1.19 | |
| The ordinary kriging | 23.4 | −31.36 | 0.8 | 8.9 | |
| The MSSHCF VS DR | 21.51 | −28.28 | 0.53 | 8.25 | |
| The ordinary kriging | 11.95 | −9.29 | 1.39 | 3.96 | |
| The MSSHCF VS SS V28 | 11.04 | −8.57 | 1.07 | 3.47 | |
| The ordinary kriging | 7.12 | −2.3 | 1.7 | 1.66 | |
| The MSSHCF VS DTU17 | 4.47 | −2.07 | 1.07 | 1.16 | |
| 50~100 | The ordinary kriging | 5.57 | −1.48 | 1.69 | 1.46 |
| The MSSHCF VS EGM2008 | 5.23 | −0.95 | 1.04 | 1.04 | |
| The ordinary kriging | 33.72 | −10.7 | 8.38 | 7.6 | |
| The MSSHCF VS DR | 33.87 | −9.86 | 7.72 | 7.14 | |
| The ordinary kriging | 8.32 | −4.14 | 1.79 | 2.42 | |
| The MSSHCF VS SS V28 | 6.6 | −4.14 | 1.17 | 1.93 | |
| The ordinary kriging | 5.12 | −5.26 | −0.08 | 1.56 | |
| The MSSHCF VS DTU17 | 3.53 | −3.45 | −0.07 | 1.16 | |
| 100~200 | The ordinary kriging | 3.0128 | −4.1208 | −0.1792 | 1.28 |
| The MSSHCF VS EGM2008 | 2.7119 | −2.9765 | −0.1255 | 0.9 | |
| The ordinary kriging | 29.24 | −16.08 | −0.31 | 6.53 | |
| The MSSHCF VS DR | 29.07 | −14.3 | −0.26 | 6.14 | |
| The ordinary kriging | 7.82 | −8.29 | 0.17 | 2.37 | |
| The MSSHCF VS SS V28 | 7.38 | −6.68 | 0.18 | 2.01 |
| Distance/km | Model Comparison Results | Max | Min | Mean | Std |
|---|---|---|---|---|---|
| The ordinary kriging | 12.53 | −5.2 | 0.39 | 4.16 | |
| The MSSHCF VS DTU17 | 7.81 | −5.36 | 0.36 | 3.62 | |
| 0~20 | The ordinary kriging | 12.1 | −6.03 | 0.32 | 4.57 |
| The MSSHCF VS EGM2008 | 5.17 | −4.34 | −0.07 | 2.49 | |
| The ordinary kriging | 38.81 | −29.58 | −1.98 | 17.11 | |
| The MSSHCF VS DR | 31.87 | −29.31 | −2.37 | 15.15 | |
| The ordinary kriging | 14.61 | −9.35 | 3.07 | 6.02 | |
| The MSSHCF VS SS V28 | 14.11 | −7.4 | 2.95 | 5.33 | |
| The ordinary kriging | 5.93 | −12.31 | −1.78 | 3.9 | |
| The MSSHCF VS DTU17 | 8.29 | −9.29 | −1.25 | 3 | |
| 20~50 | The ordinary kriging | 12.4 | −10.17 | −1.59 | 3.95 |
| The MSSHCF VS EGM2008 | 5.52 | −7.79 | −1.25 | 2.5 | |
| The ordinary kriging | 41.16 | −61.04 | −10.16 | 18.31 | |
| The MSSHCF VS DR | 34.45 | −58.74 | −9.82 | 16.98 | |
| The ordinary kriging | 11.76 | −15.39 | −2.82 | 5.01 | |
| The MSSHCF VS SS V28 | 6.99 | −16.43 | −3.01 | 4.67 | |
| The ordinary kriging | 5.58 | −8.8 | −0.29 | 2.19 | |
| The MSSHCF VS DTU17 | 4.54 | −6.86 | −0.3 | 1.96 | |
| 50~100 | The ordinary kriging | 3.6 | −6.87 | 0.1 | 1.52 |
| The MSSHCF VS EGM2008 | 2.54 | −4.93 | 0.08 | 1.24 | |
| The ordinary kriging | 21.34 | −32.71 | 1.81 | 8.02 | |
| The MSSHCF VS DR | 20.83 | −30.77 | 1.8 | 7.73 | |
| The ordinary kriging | 7.92 | −10.22 | −0.62 | 3.52 | |
| The MSSHCF VS SS V28 | 7.06 | −9.77 | −0.64 | 3.3 | |
| The ordinary kriging | 5.12 | −5.83 | −0.27 | 1.82 | |
| The MSSHCF VS DTU17 | 4.7 | −5.63 | −0.24 | 1.65 | |
| 100~200 | The ordinary kriging | 2.61 | −2.01 | −0.26 | 1.04 |
| The MSSHCF VS EGM2008 | 2.53 | −2.4 | −0.23 | 0.87 | |
| The ordinary kriging | 13.45 | −10.24 | −0.8 | 4.99 | |
| The MSSHCF VS DR | 13.57 | −10.02 | −0.78 | 4.81 | |
| The ordinary kriging | 10.38 | −7.33 | 0.69 | 2.97 | |
| The MSSHCF VS SS V28 | 10.48 | −6.99 | 0.71 | 2.82 |
| Sea Depth | Model Comparison Results | Max | Min | Mean | Std |
|---|---|---|---|---|---|
| The ordinary kriging VS SS V28 | 20.31 | −28.61 | 1.04 | 3.41 | |
| The MSSHCF VS SS V28 | 19.36 | −28.59 | 0.8 | 2.95 | |
| 0~100 | The ordinary kriging | 5.58 | −9.25 | 0.43 | 1.9 |
| The MSSHCF VS EGM2008 | 6.37 | −7.88 | 0.21 | 1.38 | |
| The ordinary kriging | 33.74 | −43.24 | 1.33 | 9.92 | |
| The MSSHCF VS DR | 33.87 | −36.13 | 1.11 | 9.37 | |
| The ordinary kriging VS DTU17 | 7.38 | −9.2 | 0.57 | 2.11 | |
| The MSSHCF VS DTU17 | 5.65 | −8.34 | 0.33 | 1.56 | |
| The ordinary kriging VS SS V28 | 7.82 | −9.26 | 0.36 | 2.48 | |
| The MSSHCF VS SS V28 | 7.77 | −7.65 | 0.31 | 2.09 | |
| 100~200 | The ordinary kriging | 3.01 | −4.12 | 0.1 | 1.4 |
| The MSSHCF VS EGM2008 | 3.2 | −3.41 | 0.08 | 1 | |
| The ordinary kriging | 16.85 | −16.12 | 1.29 | 7 | |
| The MSSHCF VS DR | 16.9 | −15.23 | 1.26 | 6.56 | |
| The ordinary kriging VS DTU17 | 4.37 | −5.54 | 0.18 | 1.6 | |
| The MSSHCF VS DTU17 | 3.65 | −3.7 | 0.13 | 1.18 | |
| The ordinary kriging VS SS V28 | 6.46 | −5.37 | −0.48 | 2.18 | |
| The MSSHCF VS SS V28 | 6.01 | −5.21 | −0.54 | 1.97 | |
| 200~500 | The ordinary kriging | 2.78 | −1.3 | 0.22 | 0.67 |
| The MSSHCF VS EGM2008 | 1.87 | −0.65 | 0.19 | 0.47 | |
| The ordinary kriging | 16.14 | −9.25 | 1.23 | 4.1 | |
| The MSSHCF VS DR | 14.84 | −8.5 | 1.2 | 3.88 | |
| The ordinary kriging VS DTU17 | 3.79 | −3.49 | 0.01 | 1.2 | |
| The MSSHCF VS DTU17 | 2.37 | −3.06 | −0.05 | 0.98 | |
| The ordinary kriging VS SS V28 | −0.49 | −2.5 | −1.38 | 0.58 | |
| 500~1000 | The MSSHCF VS SS V28 | −0.03 | −2.23 | −1.17 | 0.64 |
| The ordinary kriging | −0.12 | −0.69 | −0.42 | 0.18 | |
| The MSSHCF VS EGM2008 | −0.07 | −0.46 | −0.21 | 0.11 | |
| The ordinary kriging | −1.54 | −3.05 | −2.3 | 0.36 | |
| The MSSHCF VS DR | −1.49 | −2.57 | −2.1 | 0.32 | |
| The ordinary kriging VS DTU17 | −0.63 | −2.98 | −1.67 | 0.69 | |
| The MSSHCF VS DTU17 | −0.51 | −2.75 | −1.45 | 0.71 |
| Sea Depth | Model Comparison Results | Max | Min | Mean | Std |
|---|---|---|---|---|---|
| The ordinary kriging VS DTU17 | 12.73 | −12.43 | −1.03 | 2.63 | |
| The MSSHCF VS DTU17 | 8.29 | −12.31 | −0.43 | 1.23 | |
| 0~100 m | The ordinary kriging | 12.44 | −10.29 | −0.77 | 2.27 |
| The MSSHCF VS EGM2008 | 5.83 | −7.79 | −0.57 | 1.67 | |
| The ordinary kriging | 41.21 | −61.04 | −3.41 | 11.92 | |
| The MSSHCF VS DR | 34.45 | −58.74 | −3.21 | 11.34 | |
| The ordinary kriging VS SS V28 | 13.48 | −15.53 | −1.08 | 4.14 | |
| The MSSHCF VS SS V28 | 16.43 | −10.48 | −0.47 | 3 | |
| The ordinary kriging VS DTU17 | 5.24 | −4.18 | −0.69 | 1.55 | |
| The MSSHCF VS DTU17 | 3.8 | −3.94 | −0.23 | 1.18 | |
| 100~200 m | The ordinary kriging | 3.82 | −1.98 | −0.75 | 0.82 |
| The MSSHCF VS EGM2008 | 2.53 | −2.24 | −0.59 | 0.72 | |
| The ordinary kriging | 13.16 | −10.67 | −2.95 | 4.19 | |
| The MSSHCF VS DR | 13.46 | −10.98 | −2.8 | 4.09 | |
| The ordinary kriging VS SS V28 | 7.13 | −10.27 | −0.56 | 2.58 | |
| The MSSHCF VS SS V28 | 6.99 | −9.64 | −0.09 | 2.15 | |
| The ordinary kriging VS DTU17 | 5.96 | −5.83 | 0.37 | 2.01 | |
| The MSSHCF VS DTU17 | 5.29 | −4.75 | 0.17 | 1.6 | |
| 200~500 m | The ordinary kriging | 2.66 | −2.45 | 0.39 | 1.07 |
| The MSSHCF VS EGM2008 | 2.81 | −2.17 | 0.34 | 0.93 | |
| The ordinary kriging | 14.13 | −17.5 | 2.83 | 5.4 | |
| The MSSHCF VS DR | 14.86 | −18.02 | 2.78 | 5.25 | |
| The ordinary kriging VS SS V28 | 9.92 | −11.89 | 0.14 | 3.43 | |
| The MSSHCF VS SS V28 | 9.77 | −11.45 | −0.06 | 3.03 | |
| The ordinary kriging VS DTU17 | 5.54 | −3.1 | 1.22 | 1.76 | |
| The MSSHCF VS DTU17 | 4.13 | −5.12 | 0.45 | 1.37 | |
| 500~1000 m | The ordinary kriging | 2.62 | −1.97 | 0.91 | 0.93 |
| The MSSHCF VS EGM2008 | 2.88 | −1.96 | 0.69 | 0.77 | |
| The ordinary kriging | 14.33 | −6.61 | 4.97 | 4.39 | |
| The MSSHCF VS DR | 14.27 | −6.38 | 4.75 | 4.22 | |
| The ordinary kriging VS SS V28 | 12.27 | −5.32 | 2.53 | 2.82 | |
| The MSSHCF VS SS V28 | 10.14 | −5.24 | 1.76 | 2.41 |
| Area | Source of Results | Max | Min | Mean | Std | |
|---|---|---|---|---|---|---|
| A | The MSSHCF method | VS shipborne gravity | 13.69 | −15.94 | −4.50 | 5.39 |
| The ordinary kriging | 14.16 | −18.57 | −4.35 | 5.52 | ||
| SS V28 | 15.74 | −19.74 | −5.19 | 5.61 | ||
| DR | 30.74 | −33.74 | −5.84 | 9.98 | ||
| EGM2008 | 12.99 | −12.85 | −4.71 | 5.47 | ||
| DTU17 | 14.97 | −14.65 | −4.92 | 5.36 | ||
| B | The MSSHCF method | VS shipborne gravity | 14.15 | −15.90 | −1.07 | 5.99 |
| The ordinary kriging | 17.80 | −16.35 | −1.05 | 6.32 | ||
| SS V28 | 17.55 | −17.11 | −1.20 | 5.91 | ||
| DR | 27.66 | −17.42 | −0.51 | 6.82 | ||
| EGM2008 | 13.00 | −12.99 | −1.12 | 5.84 | ||
| DTU 17 | 15.12 | −17.36 | −1.32 | 5.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Yan, J.; Li, F. An Improved Coastal Marine Gravity Field Based on the Mean Sea Surface Height Constraint Factor Method. Remote Sens. 2022, 14, 4125. https://doi.org/10.3390/rs14164125
Zhang W, Yan J, Li F. An Improved Coastal Marine Gravity Field Based on the Mean Sea Surface Height Constraint Factor Method. Remote Sensing. 2022; 14(16):4125. https://doi.org/10.3390/rs14164125
Chicago/Turabian StyleZhang, Wensong, Jianguo Yan, and Fei Li. 2022. "An Improved Coastal Marine Gravity Field Based on the Mean Sea Surface Height Constraint Factor Method" Remote Sensing 14, no. 16: 4125. https://doi.org/10.3390/rs14164125
APA StyleZhang, W., Yan, J., & Li, F. (2022). An Improved Coastal Marine Gravity Field Based on the Mean Sea Surface Height Constraint Factor Method. Remote Sensing, 14(16), 4125. https://doi.org/10.3390/rs14164125