An MT-InSAR Data Partition Strategy for Sentinel-1A/B TOPS Data
Abstract
:1. Introduction
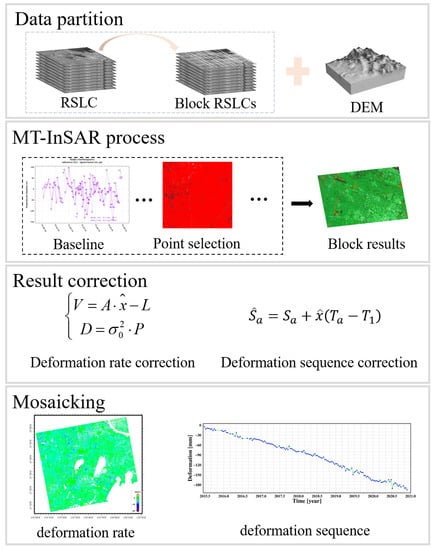
2. The Block MT-InSAR Data Processing Strategy
2.1. Data Partition and Block Processing
2.2. Results Correction Based on Least Square Estimation
2.3. Result Mosaicking
3. Experiment and Data Processing
3.1. Study Area and Datasets
3.2. Data Processing
4. Result Analysis
4.1. Precision of the Deformation Rate
4.2. Precision of the Deformation Sequence
4.3. Time and Memory Consumption
5. Discussion
5.1. Space Consistency Correction
5.2. Effects of Overlap Rate on Result Precision and Time Consumption
5.3. Implications of Data Partition Strategy for MT-InSAR
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Study Area | Parameters | Acquisition Date (YYYY/MM/DD) | ||||
|---|---|---|---|---|---|---|
| Changzhou | Direction | Ascending | 2018/01/10 | 2018/01/22 | 2018/02/03 | 2018/02/15 |
| Path | T69 | 2018/02/27 | 2018/03/11 | 2018/03/23 | 2018/04/04 | |
| Heading | −12.79° | 2018/04/16 | 2018/04/28 | 2018/05/10 | 2018/05/22 | |
| Incidence | 36.65° | 2018/06/03 | 2018/06/15 | 2018/06/27 | 2018/07/09 | |
| Pixel Spacing (Rg × Az) | 2.33 × 13.98 | 2018/07/21 | 2018/08/02 | 2018/08/14 | 2018/09/07 | |
| 2018/09/19 | 2018/10/01 | 2018/10/13 | 2018/10/25 | |||
| Number of images | 110 | 2018/11/06 | 2018/11/18 | 2018/12/12 | 2018/12/24 | |
| 2019/01/05 | 2019/01/17 | 2019/02/10 | 2019/02/16 | |||
| 2019/02/22 | 2019/03/06 | 2019/03/18 | 2019/03/30 | |||
| 2019/04/05 | 2019/04/11 | 2019/04/23 | 2019/04/29 | |||
| 2019/05/05 | 2019/05/11 | 2019/05/17 | 2019/05/23 | |||
| 2019/05/29 | 2019/06/04 | 2019/06/10 | 2019/06/16 | |||
| 2019/06/22 | 2019/06/28 | 2019/07/04 | 2019/07/10 | |||
| 2019/07/16 | 2019/07/22 | 2019/07/28 | 2019/08/03 | |||
| 2019/08/09 | 2019/08/15 | 2019/08/21 | 2019/08/27 | |||
| 2019/09/02 | 2019/09/08 | 2019/09/20 | 2019/09/26 | |||
| 2019/10/02 | 2019/10/08 | 2019/10/14 | 2019/10/20 | |||
| 2019/10/26 | 2019/11/01 | 2019/11/07 | 2019/11/19 | |||
| 2019/11/25 | 2019/12/01 | 2019/12/07 | 2019/12/13 | |||
| 2019/12/19 | 2019/12/25 | 2019/12/31 | 2020/01/12 | |||
| 2020/01/24 | 2020/02/05 | 2020/02/17 | 2020/02/29 | |||
| 2020/03/12 | 2020/03/24 | 2020/04/05 | 2020/04/17 | |||
| 2020/04/29 | 2020/05/11 | 2020/05/23 | 2020/06/04 | |||
| 2020/06/16 | 2020/06/28 | 2020/07/10 | 2020/07/22 | |||
| 2020/07/28 | 2020/08/03 | 2020/08/15 | 2020/08/27 | |||
| 2020/09/08 | 2020/09/20 | 2020/10/02 | 2020/10/14 | |||
| 2020/10/26 | 2020/11/07 | 2020/11/19 | 2020/12/01 | |||
| 2020/12/13 | 2020/12/25 | |||||
| Qijiang | Direction | Ascending | 2018/01/09 | 2018/01/21 | 2018/02/02 | 2018/02/14 |
| Path | T55 | 2018/02/26 | 2018/03/10 | 2018/03/22 | 2018/04/03 | |
| Heading | −12.65° | 2018/04/15 | 2018/04/27 | 2018/05/09 | 2018/05/21 | |
| Incidence | 43.64° | 2018/06/02 | 2018/06/14 | 2018/06/26 | 2018/07/08 | |
| Pixel Spacing (Rg × Az) | 2.33 × 13.96 | 2018/07/20 | 2018/08/01 | 2018/08/25 | 2018/09/06 | |
| 2018/09/18 | 2018/09/30 | 2018/10/12 | 2018/10/24 | |||
| Number of images | 114 | 2018/11/05 | 2018/11/29 | 2018/12/11 | 2018/12/23 | |
| 2019/01/04 | 2019/01/16 | 2019/01/28 | 2019/02/09 | |||
| 2019/02/21 | 2019/03/05 | 2019/03/17 | 2019/03/29 | |||
| 2019/04/10 | 2019/04/22 | 2019/05/04 | 2019/05/16 | |||
| 2019/05/28 | 2019/06/09 | 2019/07/03 | 2019/07/15 | |||
| 2019/07/27 | 2019/08/08 | 2019/08/20 | 2019/09/01 | |||
| 2019/09/13 | 2019/09/25 | 2019/10/07 | 2019/10/19 | |||
| 2019/10/31 | 2019/11/12 | 2019/11/24 | 2019/12/06 | |||
| 2019/12/18 | 2019/12/30 | 2020/01/11 | 2020/01/23 | |||
| 2020/02/04 | 2020/02/16 | 2020/02/28 | 2020/03/11 | |||
| 2020/03/23 | 2020/04/04 | 2020/04/16 | 2020/04/28 | |||
| 2020/05/22 | 2020/06/03 | 2020/06/15 | 2020/06/27 | |||
| 2020/07/09 | 2020/07/21 | 2020/08/02 | 2020/08/14 | |||
| 2020/09/07 | 2020/09/19 | 2020/10/01 | 2020/10/13 | |||
| 2020/10/25 | 2020/11/06 | 2020/11/18 | 2020/11/30 | |||
| 2020/12/12 | 2020/12/24 | 2021/01/05 | 2021/01/17 | |||
| 2021/01/29 | 2021/02/10 | 2021/02/22 | 2021/03/06 | |||
| 2021/03/18 | 2021/03/30 | 2021/04/11 | 2021/04/23 | |||
| 2021/05/29 | 2021/06/10 | 2021/06/22 | 2021/07/16 | |||
| 2021/07/28 | 2021/08/09 | 2021/08/21 | 2021/09/02 | |||
| 2021/09/14 | 2021/09/26 | 2021/10/08 | 2021/10/20 | |||
| 2021/11/01 | 2021/11/13 | 2021/11/25 | 2021/12/07 | |||
| 2021/12/19 | 2021/12/31 | |||||


References
- Ng, A.H.-M.; Ge, L.; Li, X.; Zhang, K. Monitoring ground deformation in Beijing, China with persistent scatterer SAR interferometry. J. Geod. 2011, 86, 375–392. [Google Scholar] [CrossRef]
- Wang, H.; Wright, T.J.; Yu, Y.; Lin, H.; Jiang, L.; Li, C.; Qiu, G. InSAR reveals coastal subsidence in the Pearl River Delta, China. Geophys. J. Int. 2012, 191, 1119–1128. [Google Scholar] [CrossRef]
- Feng, G.; Li, Z.; Shan, X.; Xu, B.; Du, Y. Source parameters of the 2014 Mw 6.1 South Napa earthquake estimated from the Sentinel 1A, COSMO-SkyMed and GPS data. Tectonophysics 2015, 655, 139–146. [Google Scholar] [CrossRef]
- Chaussard, E.; Johnson, C.W.; Fattahi, H.; Bürgmann, R. Potential and limits of InSAR to characterize interseismic deformation independently of GPS data: Application to the southern San Andreas Fault system. Geochem. Geophys. Geosystems 2016, 17, 1214–1229. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Tang, M.; Liao, M.; Xu, Q.; Gong, J.; Ao, M. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: A case study of Jiaju landslide in Danba, China. Remote Sens. Environ. 2018, 205, 180–198. [Google Scholar] [CrossRef]
- Xiong, Z.; Feng, G.; Feng, Z.; Miao, L.; Wang, Y.; Yang, D.; Luo, S. Pre- and post-failure spatial-temporal deformation pattern of the Baige landslide retrieved from multiple radar and optical satellite images. Eng. Geol. 2020, 279, 105580. [Google Scholar] [CrossRef]
- Novellino, A.; Cesarano, M.; Cappelletti, P.; di Martire, D.; di Napoli, M.; Ramondini, M.; Sowter, A.; Calcaterra, D. Slow-moving landslide risk assessment combining Machine Learning and InSAR techniques. CATENA 2021, 203, 105317. [Google Scholar] [CrossRef]
- Meng, Q.; Confuorto, P.; Peng, Y.; Raspini, F.; Bianchini, S.; Han, S.; Liu, H.; Casagli, N. Regional Recognition and Classification of Active Loess Landslides Using Two-Dimensional Deformation Derived from Sentinel-1 Interferometric Radar Data. Remote Sens. 2020, 12, 1541. [Google Scholar] [CrossRef]
- Miele, P.; Di Napoli, M.; Novellino, A.; Calcaterra, D.; Mallorqui, J.J.; Di Martire, D. SAR data and field surveys combination to update rainfall-induced shallow landslide inventory. Remote Sens. Appl. Soc. Environ. 2022, 26, 100755. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Preusse, A.; Hu, J.; Feng, G.; Papst, M. High-Resolution Three-Dimensional Displacement Retrieval of Mining Areas From a Single SAR Amplitude Pair Using the SPIKE Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3782–3793. [Google Scholar] [CrossRef]
- Ghasemloo, N.; Matkan, A.A.; Alimohammadi, A.; Aghighi, H.; Mirbagheri, B. Estimating the Agricultural Farm Soil Moisture Using Spectral Indices of Landsat 8, and Sentinel-1, and Artificial Neural Networks. J. Geov. Spat. Anal. 2022, 6, 19. [Google Scholar] [CrossRef]
- Kellogg, K.; Hoffman, P.; Standley, S.; Shaffer, S.; Rosen, P.; Edelstein, W.; Dunn, C.; Baker, C.; Barela, P.; Shen, Y.; et al. NASA-ISRO Synthetic Aperture Radar (NISAR) Mission. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–21. [Google Scholar] [CrossRef]
- Fan, W.; Pan, G.; Wang, L. Development and Application of a Networked Automatic Deformation Monitoring System. J. Geovisualization Spat. Anal. 2020, 4, 11. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Wang, C.; Tang, Y.; Zhang, H.; You, H.; Zhang, W.; Duan, W.; Wang, J.; Dong, L.; Zhang, B. First mapping of China surface movement using supercomputing interferometric SAR technique. Sci. Bull. 2021, 66, 1608–1610. [Google Scholar] [CrossRef]
- De Luca, C.; Cuccu, R.; Elefante, S.; Zinno, I.; Manunta, M.; Casola, V.; Rivolta, G.; Lanari, R.; Casu, F. An On-Demand Web Tool for the Unsupervised Retrieval of Earth’s Surface Deformation from SAR Data: The P-SBAS Service within the ESA G-POD Environment. Remote Sens. 2015, 7, 15630–15650. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 11. [Google Scholar] [CrossRef]
- Zhang, K.; Ge, L.; Hu, Z.; Ng, A.H.-M.; Li, X.; Rizos, C. Phase Unwrapping for Very Large Interferometric Data Sets. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4048–4061. [Google Scholar] [CrossRef]
- Yu, H.; Xing, M.; Bao, Z. A Fast Phase Unwrapping Method for Large-Scale Interferograms. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4240–4248. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, T.; Xing, X.; Peng, W.; Chen, L. BM3D Denoising for a Cluster-Analysis-Based Multibaseline InSAR Phase-Unwrapping Method. Remote Sens. 2022, 14, 1836. [Google Scholar] [CrossRef]
- Du, Y.; Fu, H.; Liu, L.; Feng, G.; Peng, X.; Wen, D. Orbit error removal in InSAR/MTInSAR with a patch-based polynomial model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102438. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, L.; Ding, X.; Lu, Z.; Li, X. Toward Mitigating Stratified Tropospheric Delays in Multitemporal InSAR: A Quadtree Aided Joint Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 291–303. [Google Scholar] [CrossRef]
- Shi, M.; Peng, J.; Chen, X.; Zheng, Y.; Yang, H.; Su, Y.; Wang, G.; Wang, W. An Improved Method for InSAR Atmospheric Phase Correction in Mountainous Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10509–10519. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N.; Shau, R.; Rodriguez-Gonzalez, F. Improving the reference network in wide-area Persistent Scatterer Interferometry for non-urban areas. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1448–1451. [Google Scholar] [CrossRef]
- Xue, F.; Lv, X.; Dou, F.; Yun, Y. A Review of Time-Series Interferometric SAR Techniques: A Tutorial for Surface Deformation Analysis. IEEE Geosci. Remote Sens. Mag. 2020, 8, 22–42. [Google Scholar] [CrossRef]
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the IGARSS 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 4367, pp. 4362–4364. [Google Scholar] [CrossRef]
- Li, T.; Liu, G.; Lin, H.; Jia, H.; Zhang, R.; Yu, B.; Luo, Q. A Hierarchical Multi-Temporal InSAR Method for Increasing the Spatial Density of Deformation Measurements. Remote Sens. 2014, 6, 3349–3368. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, 16. [Google Scholar] [CrossRef]
- Hou, J.; Xu, B.; Li, Z.; Zhu, Y.; Feng, G. Block PS-InSAR ground deformation estimation for large-scale areas based on network adjustment. J. Geod. 2021, 95, 111. [Google Scholar] [CrossRef]
- Ge, D. Research on Key Technologies for Regional Ground Subsidence InSAR Monitoring. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2013. [Google Scholar]
- Liu, H.; Yu, J.; Zhao, Z.; Jezek, K.C. Calibrating and mosaicking surface velocity measurements from interferometric SAR data with a simultaneous least-squares adjustment approach. Int. J. Remote Sens. 2007, 28, 1217–1230. [Google Scholar] [CrossRef]
- Hu, J. Theory and Methodology of InSAR Three-Dimensional Deformation Estimation Based on Modern Measurement Leveling. Ph.D. Thesis, Central South University, Changsha, China, 2013. [Google Scholar]
- Kalia, A.C.; Frei, M.; Lege, T. A Copernicus downstream-service for the nationwide monitoring of surface displacements in Germany. Remote Sens. Environ. 2017, 202, 234–249. [Google Scholar] [CrossRef]
- Murray, K.D.; Lohman, R.B.; Bekaert, D.P.S. Cluster-Based Empirical Tropospheric Corrections Applied to InSAR Time Series Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2204–2212. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating. Earth-Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, G.; Li, Z.; Luo, S.; Wang, H.; Xiong, Z.; Zhu, J.; Hu, J. A Strategy for Variable-Scale InSAR Deformation Monitoring in a Wide Area: A Case Study in the Turpan–Hami Basin, China. Remote Sens. 2022, 14, 3832. [Google Scholar] [CrossRef]
- Luo, S.; Feng, G.; Xiong, Z.; Wang, H.; Zhao, Y.; Li, K.; Deng, K.; Wang, Y. An Improved Method for Automatic Identification and Assessment of Potential Geohazards Based on MT-InSAR Measurements. Remote Sens. 2021, 13, 3490. [Google Scholar] [CrossRef]
- Zhong, Y.; Dong, S.; Hu, H. Monitoring and Analysis of Ground Settlement in Changzhou City Based on Time-Series InSAR Technology. Geol. J. China Univ. 2019, 25, 131–143. [Google Scholar]
- Wang, J.; Wei, Z.; Liu, W.; Zhong, S.; Zhang, G. Functional zoning of land consolidation in mountainous and hilly areas based on “Production-ecological” perspective: A case study of Qijiang District, Chongqing. Areal Res. Dev. 2018, 37, 155–159. [Google Scholar]
- Williams, S.; Bock, Y.; Fang, P. Integrated satellite interferometry: Tropospheric noise, GPS estimates and implications for interferometric synthetic aperture radar products. J. Geophys. Res. Solid Earth 1998, 103, 27051–27067. [Google Scholar] [CrossRef]








| Study Area | Direction | Path | Heading | Incidence | Pixel Spacing (Rg × Az) | Num of Images |
|---|---|---|---|---|---|---|
| Changzhou | Ascending | T69 | −12.79° | 36.65° | 2.33 × 13.98 m | 110 |
| Qijiang | T55 | −12.65° | 43.64° | 2.33 × 13.96 m | 115 |
| Study Area | Strategy | Area | Number of Points | Std /(mm/yr) | Mean /(mm/yr) | Difference /(mm/yr) | Precision Improvement |
|---|---|---|---|---|---|---|---|
| Changzhou | Partition | A | 564,867 | 3.4 | 4.0 | 0.2 | 5% |
| B | 589,430 | 4.1 | |||||
| C | 593,479 | 4.6 | |||||
| Traditional | A | 561,071 | 3.7 | 4.2 | |||
| B | 582,648 | 4.2 | |||||
| C | 591,199 | 4.6 | |||||
| Qijiang | Partition | D | 992,679 | 3.2 | 3.3 | 0.6 | 15% |
| E | 916,098 | 3.1 | |||||
| F | 922,811 | 3.6 | |||||
| Traditional | D | 986,163 | 3.8 | 3.9 | |||
| E | 897,871 | 3.9 | |||||
| F | 923,017 | 4.0 |
| Changzhou | Qijiang | |||
|---|---|---|---|---|
| Traditional | Partition | Traditional | Partition | |
| Original size (pixels) | 29,739 × 6892 | 29,739 × 6892 | 28,104 × 7648 | 28,104 × 7648 |
| Partition strategy | \ | 6 × 5 ~30% overlap | \ | 6 × 5 ~25% overlap |
| Size of block (pixels) | \ | 7147 × 1373 | \ | 6374 × 1574 |
| Platform | CPU: AMD Ryzen 9 5900X 12-Core/RAM:64 G | |||
| Multi-look | 5:1 | |||
| Average number of points in a block | \ | 2,941,200 | \ | 2,493,200 |
| Total number of points | 50,941,512 | 51,178,814 | 51,620,120 | 51,883,633 |
| Memory Usage | 27.2 G | 1.3 G | 27.9 G | 1.3 G |
| Time of partition | \ | ~1 h | \ | ~1 h |
| Time of InSAR processing | ~20 h | ~1.2 h | ~20 h | ~1.2 h |
| Time of correction | \ | ~0.1 h | \ | ~0.1 h |
| Total time | ~20 h | ~8.7 h | ~20 h | ~8.7 h |
| Overlap Ratio | Total Overlap | Block Size (Amount) | Precision /(mm/yr) | Time of Each Block | Total Time | |
|---|---|---|---|---|---|---|
| Traditional | 0% | 29,739 × 6892 (1) | A | 3.7 | 20 h | 20 h |
| B | 4.2 | |||||
| C | 4.6 | |||||
| 10% | 36% | 7000 × 1500 (20) 4539 × 1500 (5) | A1 | 3.5 | 1.2 h 0.8 h | 6.7 h |
| B1 | 4.2 | |||||
| C1 | 4.6 | |||||
| 20% | 64% | 7000 × 1500 (25) 7000 × 892 (5) | A2 | 3.5 | 1.2 h 0.7 h | 7.8 h |
| B2 | 4.1 | |||||
| C2 | 4.6 | |||||
| 30% | 84% | 7000 × 1500 (30) 5239 × 1500 (6) | A3 | 3.4 | 1.2 h 0.9 h | 10.1 h |
| B3 | 4.1 | |||||
| C3 | 4.6 | |||||
| 40% | 96% | 7000 × 1500 (42) 4539 × 1500 (7) | A4 | 3.3 | 1.2 h 0.8 h | 12.7 h |
| B4 | 4.0 | |||||
| C4 | 4.5 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Feng, G.; Feng, Z.; Wang, Y.; Wang, X.; Luo, S.; Zhao, Y.; Lu, H. An MT-InSAR Data Partition Strategy for Sentinel-1A/B TOPS Data. Remote Sens. 2022, 14, 4562. https://doi.org/10.3390/rs14184562
Wang Y, Feng G, Feng Z, Wang Y, Wang X, Luo S, Zhao Y, Lu H. An MT-InSAR Data Partition Strategy for Sentinel-1A/B TOPS Data. Remote Sensing. 2022; 14(18):4562. https://doi.org/10.3390/rs14184562
Chicago/Turabian StyleWang, Yuexin, Guangcai Feng, Zhixiong Feng, Yuedong Wang, Xiuhua Wang, Shuran Luo, Yinggang Zhao, and Hao Lu. 2022. "An MT-InSAR Data Partition Strategy for Sentinel-1A/B TOPS Data" Remote Sensing 14, no. 18: 4562. https://doi.org/10.3390/rs14184562
APA StyleWang, Y., Feng, G., Feng, Z., Wang, Y., Wang, X., Luo, S., Zhao, Y., & Lu, H. (2022). An MT-InSAR Data Partition Strategy for Sentinel-1A/B TOPS Data. Remote Sensing, 14(18), 4562. https://doi.org/10.3390/rs14184562