Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer
Abstract
:1. Introduction
2. Methods
2.1. Representation and Preprocessing of PolSAR Image
2.2. Typical CNN-Based Method and Dilated Convolution
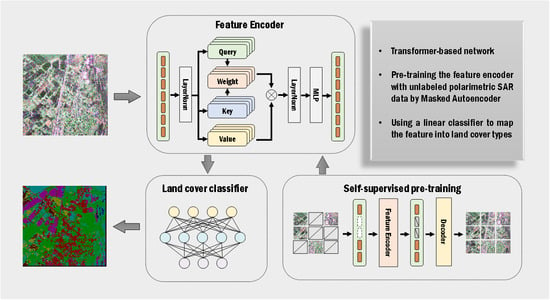
2.3. The Proposed Land Cover Classification Method
2.3.1. Feature Embedding
2.3.2. Feature Encoder
2.3.3. Land Cover Classifier
2.4. Pre-Training Method
3. Results
3.1. Data Description
3.2. Pre-Training Settings and Results
3.3. Land Cover Classification Experiments
3.3.1. Comparison Experiments
3.3.2. Ablation Experiments
4. Discussion
4.1. Influence of Receptive Field
4.2. Potential Overfitting Problem
4.3. Expected Performance on Complicated Classification Tasks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kong, J.; Swartz, A.; Yueh, H.; Novak, L.; Shin, R. Identification of terrain cover using the optimum polarimetric classifier. J. Electromagn. Waves Appl. 1988, 2, 171–194. [Google Scholar]
- Lim, H.; Swartz, A.; Yueh, H.; Kong, J.A.; Shin, R.; Van Zyl, J. Classification of earth terrain using polarimetric synthetic aperture radar images. J. Geophys. Res. Solid Earth 1989, 94, 7049–7057. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Lee, J.; Schuler, D.; Lang, R.; Ranson, K. K-distribution for multi-look processed polarimetric SAR imagery. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 4, pp. 2179–2181. [Google Scholar]
- Freitas, C.C.; Frery, A.C.; Correia, A.H. The polarimetric G distribution for SAR data analysis. Environmetrics Off. J. Int. Environmetrics Soc. 2005, 16, 13–31. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Zhang, P.; Wu, Y.; Jia, L.; An, L. The WGΓ distribution for multilook polarimetric SAR data and its application. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2056–2060. [Google Scholar] [CrossRef]
- Gao, W.; Yang, J.; Ma, W. Land cover classification for polarimetric SAR images based on mixture models. Remote Sens. 2014, 6, 3770–3790. [Google Scholar] [CrossRef]
- Wu, Y.; Ji, K.; Yu, W.; Su, Y. Region-based classification of polarimetric SAR images using Wishart MRF. IEEE Geosci. Remote Sens. Lett. 2008, 5, 668–672. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Zhang, P.; Wu, Y.; Tan, X.; An, L. Mixture WG-Γ-MRF Model for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 905–920. [Google Scholar] [CrossRef]
- Yin, J.; Liu, X.; Yang, J.; Chu, C.Y.; Chang, Y.L. PolSAR image classification based on statistical distribution and MRF. Remote Sens. 2020, 12, 1027. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Lardeux, C.; Frison, P.L.; Tison, C.; Souyris, J.C.; Stoll, B.; Fruneau, B.; Rudant, J.P. Support Vector Machine for Multifrequency SAR Polarimetric Data Classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4143–4152. [Google Scholar] [CrossRef]
- Masjedi, A.; Zoej, M.J.V.; Maghsoudi, Y. Classification of polarimetric SAR images based on modeling contextual information and using texture features. IEEE Trans. Geosci. Remote Sens. 2015, 54, 932–943. [Google Scholar] [CrossRef]
- Song, W.; Wu, Y.; Guo, P. Composite kernel and hybrid discriminative random field model based on feature fusion for PolSAR image classification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1069–1073. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L.; Zou, B. PolSAR Image Classification with Lightweight 3D Convolutional Networks. Remote Sens. 2020, 12, 396. [Google Scholar] [CrossRef]
- Chen, S.W.; Tao, C.S. PolSAR image classification using polarimetric-feature-driven deep convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 627–631. [Google Scholar] [CrossRef]
- Yang, C.; Hou, B.; Ren, B.; Hu, Y.; Jiao, L. CNN-based polarimetric decomposition feature selection for PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8796–8812. [Google Scholar] [CrossRef]
- Xie, W.; Ma, G.; Zhao, F.; Liu, H.; Zhang, L. PolSAR image classification via a novel semi-supervised recurrent complex-valued convolution neural network. Neurocomputing 2020, 388, 255–268. [Google Scholar] [CrossRef]
- Liu, F.; Jiao, L.; Tang, X. Task-Oriented GAN for PolSAR Image Classification and Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2707–2719. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Z.; Zhang, T.; Guo, W.; Luo, Y. Transferable SAR Image Classification Crossing Different Satellites Under Open Set Condition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Ramachandran, P.; Parmar, N.; Vaswani, A.; Bello, I.; Levskaya, A.; Shlens, J. Stand-alone self-attention in vision models. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Wang, H.; Zhu, Y.; Green, B.; Adam, H.; Yuille, A.; Chen, L.C. Axial-deeplab: Stand-alone axial-attention for panoptic segmentation. In Proceedings of the European Conference on Computer Vision 2020, Online, 23–28 August 2020; 2020; pp. 108–126. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision 2020, Online, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Online, 26 April–1 May 2020. [Google Scholar]
- Mahajan, D.; Girshick, R.; Ramanathan, V.; He, K.; Paluri, M.; Li, Y.; Bharambe, A.; Van Der Maaten, L. Exploring the limits of weakly supervised pretraining. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 181–196. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the International Conference on Machine Learning, Online, 13–15 September 2021; pp. 10347–10357. [Google Scholar]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 7262–7272. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Goyal, P.; Mahajan, D.; Gupta, A.; Misra, I. Scaling and benchmarking self-supervised visual representation learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6391–6400. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning 2020, Online, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Chen, X.; Fan, H.; Girshick, R.; He, K. Improved baselines with momentum contrastive learning. arXiv 2020, arXiv:2003.04297. [Google Scholar]
- Chen, X.; Xie, S.; He, K. An empirical study of training self-supervised vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 9640–9649. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21 June 2022; pp. 16000–16009. [Google Scholar]
- Devlin, J.; Chang, M.W.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the NAACL-HLT 2019, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Dong, H.; Zhang, L.; Zou, B. Exploring Vision Transformers for Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, F.; Jiao, L.; Guo, Y.; Liang, X.; Li, L.; Yang, S.; Qian, X. Polarimetric multipath convolutional neural network for PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2017. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Bridging nonlinearities and stochastic regularizers with gaussian error linear units. arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Zhang, L.; Zhang, S.; Zou, B.; Dong, H. Unsupervised Deep Representation Learning and Few-Shot Classification of PolSAR Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, L.; Jiao, L.; Ma, W.; Duan, Y.; Zhang, D. PolSAR image classification based on multi-scale stacked sparse autoencoder. Neurocomputing 2019, 351, 167–179. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Vancouver, BC, Canada, 2019; pp. 8024–8035. [Google Scholar]
- Dongling, X.; Chang, L. PolSAR Terrain Classification Based on Fine-tuned Dilated Group-cross Convolution Neural Network. J. Radars 2019, 8, 479–489. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations; 2018. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]















| Time Consumption (s) | The Required Numbers of Foward Propagations | Computation Costs in a Single Propagation (FLOP) | Computation Costs for the Whole Image (FLOP) | |
|---|---|---|---|---|
| Silding-window-based CNN | 28.55 | 6.25 M | 0.35 M | 2.19 T |
| The proposed method | 10.43 | 196 | 12.76 G | 2.50 T |
| Method | CNN [19] | CV-CNN [20] | 3D-CNN [21] | SViT [43] | WMM [7] | SVM [14] | The Proposed Method |
|---|---|---|---|---|---|---|---|
| Potato | 93.61 | 93.03 | 87.37 | 94.68 | 80.13 | 71.01 | 98.02 |
| Beet | 76.77 | 73.51 | 53.26 | 88.84 | 20.73 | 20.95 | 98.45 |
| Wheat | 95.89 | 95.32 | 91.60 | 97.44 | 88.74 | 88.89 | 99.40 |
| Barley | 94.33 | 95.00 | 90.93 | 98.10 | 54.73 | 35.52 | 99.19 |
| Beans | 95.90 | 96.02 | 81.23 | 99.67 | 67.71 | 40.30 | 99.92 |
| Flax | 92.98 | 94.30 | 88.25 | 99.23 | 51.37 | 33.73 | 99.93 |
| Peas | 94.63 | 92.71 | 84.26 | 98.67 | 75.50 | 75.59 | 100.00 |
| Rapeseed | 98.17 | 98.49 | 97.98 | 99.15 | 95.28 | 99.33 | 99.26 |
| Building | 87.26 | 91.73 | 87.71 | 95.58 | 74.85 | 88.17 | 99.88 |
| Maize | 90.22 | 87.40 | 72.67 | 97.74 | 52.77 | 54.36 | 100.00 |
| Grass | 82.33 | 81.63 | 61.19 | 92.77 | 9.53 | 32.19 | 97.93 |
| Fruit | 90.40 | 93.93 | 90.50 | 96.94 | 86.92 | 87.23 | 99.33 |
| Lucerne | 95.24 | 95.12 | 87.63 | 99.68 | 78.93 | 23.79 | 100.00 |
| Oats | 99.63 | 99.89 | 98.98 | 99.95 | 89.08 | 77.68 | 100.00 |
| Onions | 96.01 | 96.83 | 80.63 | 99.76 | 36.65 | 44.55 | 100.00 |
| Roads | 74.09 | 76.14 | 64.09 | 82.21 | 32.40 | 29.95 | 92.24 |
| Kappa | 0.8863 | 0.8861 | 0.8022 | 0.9373 | 0.5948 | 0.5455 | 0.9789 |
| OA | 90.00 | 89.97 | 82.44 | 94.52 | 63.08 | 58.26 | 98.16 |
| Method | CNN [19] | CV-CNN [20] | 3D-CNN [21] | SViT [43] | WMM [7] | SVM [14] | The Proposed Method |
|---|---|---|---|---|---|---|---|
| Potato | 96.60 | 96.71 | 93.37 | 97.28 | 96.65 | 97.91 | 99.19 |
| Beet | 91.41 | 92.37 | 79.14 | 95.32 | 36.32 | 57.08 | 97.27 |
| Wheat | 96.28 | 96.68 | 93.23 | 97.62 | 85.13 | 94.71 | 99.71 |
| Barley | 97.55 | 97.83 | 95.39 | 98.34 | 84.32 | 52.90 | 99.55 |
| Beans | 99.51 | 99.14 | 92.27 | 99.79 | 97.42 | 97.86 | 100.00 |
| Flax | 99.33 | 99.74 | 99.50 | 99.99 | 93.63 | 98.20 | 100.00 |
| Peas | 98.50 | 98.73 | 90.78 | 99.59 | 75.29 | 78.07 | 99.97 |
| Rapeseed | 99.54 | 99.68 | 99.38 | 99.70 | 92.42 | 99.64 | 99.94 |
| Building | 89.43 | 92.83 | 87.32 | 95.97 | 31.25 | 67.63 | 98.71 |
| Maize | 97.78 | 97.95 | 91.90 | 99.50 | 45.45 | 75.38 | 100.00 |
| Grass | 92.41 | 93.17 | 85.51 | 95.12 | 29.64 | 67.52 | 97.49 |
| Fruit | 96.71 | 98.38 | 97.28 | 99.03 | 96.54 | 91.69 | 99.79 |
| Lucerne | 99.76 | 99.85 | 98.67 | 99.93 | 92.25 | 94.36 | 100.00 |
| Oats | 100.00 | 99.97 | 99.90 | 99.99 | 99.90 | 99.98 | 100.00 |
| Onions | 99.09 | 98.96 | 93.78 | 99.85 | 77.63 | 36.86 | 100.00 |
| Roads | 80.37 | 83.34 | 70.95 | 86.93 | 26.23 | 24.35 | 93.29 |
| Kappa | 0.9366 | 0.9451 | 0.8878 | 0.9594 | 0.6969 | 0.7158 | 0.9831 |
| OA | 94.46 | 95.20 | 90.12 | 96.46 | 72.76 | 74.41 | 98.52 |
| Method | CNN [19] | CV-CNN [20] | 3D-CNN [21] | SViT [43] | WMM [7] | SVM [14] | The Proposed Method |
|---|---|---|---|---|---|---|---|
| Potato | 92.74 | 95.52 | 93.16 | 96.58 | 83.71 | 95.24 | 99.27 |
| Beet | 74.92 | 81.31 | 69.77 | 89.94 | 2.00 | 30.58 | 98.41 |
| Wheat | 87.34 | 90.89 | 88.86 | 93.19 | 85.19 | 32.94 | 99.64 |
| Barley | 86.74 | 90.91 | 89.10 | 95.48 | 52.19 | 55.98 | 99.55 |
| Beans | 99.80 | 99.96 | 99.70 | 99.95 | 99.92 | 100.00 | 100.00 |
| Flax | 99.62 | 99.79 | 99.66 | 99.90 | 90.57 | 99.30 | 100.00 |
| Peas | 95.78 | 97.58 | 90.88 | 99.52 | 85.85 | 65.81 | 100.00 |
| Rapeseed | 99.87 | 99.86 | 99.62 | 99.69 | 100.00 | 99.70 | 99.99 |
| Building | 83.82 | 88.04 | 82.07 | 95.27 | 26.78 | 49.19 | 97.07 |
| Maize | 87.87 | 90.98 | 83.86 | 97.16 | 44.64 | 29.53 | 100.00 |
| Grass | 90.76 | 92.92 | 89.51 | 95.91 | 41.17 | 56.01 | 99.04 |
| Fruit | 82.71 | 91.18 | 87.81 | 97.60 | 32.24 | 47.35 | 99.81 |
| Lucerne | 86.12 | 94.39 | 89.91 | 99.11 | 53.72 | 25.24 | 100.00 |
| Oats | 99.46 | 99.91 | 99.96 | 99.99 | 98.82 | 96.13 | 100.00 |
| Onions | 99.61 | 99.58 | 99.28 | 99.98 | 58.62 | 89.53 | 100.00 |
| Roads | 75.62 | 80.02 | 70.60 | 83.27 | 20.35 | 12.56 | 92.36 |
| Kappa | 0.8541 | 0.8947 | 0.8514 | 0.9309 | 0.5584 | 0.5053 | 0.9839 |
| OA | 87.08 | 90.73 | 86.85 | 93.94 | 59.59 | 53.92 | 98.60 |
| Method | CNN [19] | CV-CNN [20] | 3D-CNN [21] | SViT [43] | CNN-Dilated | CV-CNN-Dilated | 3D-CNN-Dilated | SViT-Larger | The Proposed Method | |
|---|---|---|---|---|---|---|---|---|---|---|
| L | Buildings | 42.73 | 46.58 | 45.37 | 54.58 | 84.90 | 81.02 | 75.02 | 83.84 | 95.25 |
| Crops | 47.55 | 56.17 | 58.31 | 61.30 | 78.55 | 78.45 | 80.55 | 78.23 | 95.39 | |
| Moss | 20.81 | 20.70 | 17.06 | 26.12 | 60.83 | 60.59 | 45.24 | 60.55 | 87.70 | |
| Roads | 49.09 | 53.23 | 53.51 | 56.67 | 73.47 | 70.18 | 68.18 | 71.26 | 91.29 | |
| Trees | 64.20 | 73.64 | 76.30 | 76.54 | 89.37 | 90.99 | 89.91 | 87.59 | 96.85 | |
| Water | 76.41 | 79.63 | 79.09 | 79.68 | 87.15 | 85.56 | 83.05 | 83.98 | 95.50 | |
| Kappa | 0.5017 | 0.5619 | 0.5673 | 0.5932 | 0.7698 | 0.7670 | 0.7321 | 0.7492 | 0.9296 | |
| OA | 58.44 | 64.13 | 64.65 | 66.93 | 82.05 | 81.81 | 78.94 | 80.31 | 94.71 | |
| C | Buildings | 52.72 | 57.49 | 51.84 | 69.94 | 89.96 | 86.90 | 80.21 | 90.53 | 97.44 |
| Crops | 38.68 | 43.59 | 43.90 | 54.36 | 84.03 | 85.46 | 82.13 | 84.61 | 96.86 | |
| Moss | 36.63 | 39.32 | 37.77 | 44.52 | 73.44 | 70.59 | 55.57 | 71.43 | 94.12 | |
| Roads | 49.81 | 54.39 | 59.61 | 61.56 | 81.50 | 77.43 | 75.77 | 82.78 | 94.72 | |
| Trees | 44.55 | 58.25 | 62.92 | 60.91 | 85.26 | 85.65 | 79.40 | 82.18 | 97.30 | |
| Water | 75.06 | 77.26 | 78.06 | 80.53 | 94.34 | 93.09 | 84.10 | 91.29 | 97.99 | |
| Kappa | 0.4463 | 0.5089 | 0.5241 | 0.5639 | 0.8241 | 0.8179 | 0.7254 | 0.7993 | 0.9592 | |
| OA | 52.83 | 58.94 | 60.43 | 64.07 | 86.47 | 85.97 | 78.30 | 84.44 | 96.96 | |
| Ka | Buildings | 57.95 | 66.84 | 65.04 | 74.00 | 91.31 | 88.75 | 84.14 | 92.19 | 97.89 |
| Crops | 42.48 | 49.47 | 45.42 | 63.75 | 87.47 | 86.28 | 74.53 | 84.40 | 97.14 | |
| Moss | 43.73 | 53.76 | 57.66 | 61.41 | 78.22 | 76.52 | 63.67 | 77.88 | 94.60 | |
| Roads | 44.76 | 52.81 | 47.91 | 60.12 | 86.34 | 83.71 | 72.70 | 84.63 | 95.71 | |
| Trees | 53.46 | 59.59 | 58.44 | 66.55 | 87.47 | 83.41 | 75.05 | 86.83 | 97.24 | |
| Water | 74.76 | 77.50 | 76.22 | 79.59 | 93.59 | 92.56 | 84.10 | 89.89 | 98.70 | |
| Kappa | 0.4888 | 0.5499 | 0.5373 | 0.6268 | 0.8475 | 0.8221 | 0.7049 | 0.8205 | 0.9642 | |
| OA | 56.94 | 62.68 | 61.47 | 69.65 | 88.32 | 86.27 | 76.52 | 86.13 | 97.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Xing, C.; Yin, J.; Yang, J. Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sens. 2022, 14, 4656. https://doi.org/10.3390/rs14184656
Wang H, Xing C, Yin J, Yang J. Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sensing. 2022; 14(18):4656. https://doi.org/10.3390/rs14184656
Chicago/Turabian StyleWang, Hongmiao, Cheng Xing, Junjun Yin, and Jian Yang. 2022. "Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer" Remote Sensing 14, no. 18: 4656. https://doi.org/10.3390/rs14184656
APA StyleWang, H., Xing, C., Yin, J., & Yang, J. (2022). Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sensing, 14(18), 4656. https://doi.org/10.3390/rs14184656