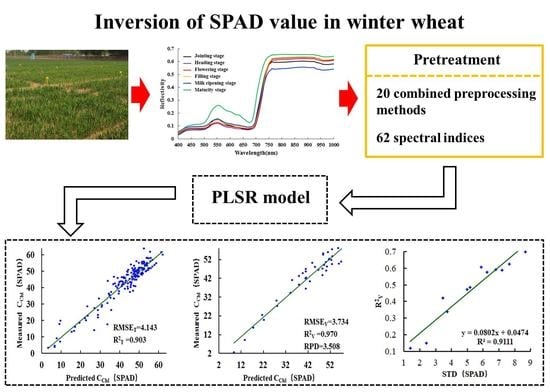
Winter Wheat SPAD Value Inversion Based on Multiple Pretreatment Methods

Abstract

SPAD value was measured by a portable chlorophyll instrument, which can reflect the relative chlorophyll content of vegetation well. Chlorophyll is an important organic chemical substance in plants that acquires and transmits energy during photosynthesis. The continuous spectral curve of winter wheat can be obtained rapidly in a specific band range by using hyperspectral remote sensing technology to estimate the SPAD value of winter wheat, which is of great significance to the growth monitoring and yield estimation research of winter wheat. In this study, with winter wheat as the research object, the spectral data and corresponding SPAD value in different growth stages were used as the data source, 20 kinds of data preprocessing spectra and sensitive spectral indices set the data as model input values, the partial least square regression (PLSR) model was established to estimate the SPAD value, and the model estimation results of different model input values at different growth stages were compared in detail. The results showed that the set of sensitive spectral indices selected in this study as input values can effectively improve the accuracy and stability of the PLSR model. In addition, the effects of 20 spectral data pretreatment methods on the estimation results of the SPAD value were compared and analyzed in different growth stages. It was found that the spectral data pretreated by the combination of wavelet packet denoising, first-order derivative transformation and principal component analysis can improve the accuracy and stability of PLSR model, and it is suitable for all growth stages. The results also showed that the estimation model is highly sensitive to the standard deviation of the SPAD value (STD_chl) in sample sets. When the standard deviation is greater than 5.5 SPAD, the larger the STD_chl is, the higher the model estimation accuracy is, and the more stable the model is. At this time, the model estimation accuracy is higher (R²_V is greater than 0.5, ratio of performance to deviation is greater than 1.4), which can meet the estimation requirements of the SPAD value.

1. Introduction

Chlorophyll is the main pigment in plants that aids in photosynthesis and plays a great role in the acquisition and transmission of energy in plants [1,2]. As an important index to evaluate the healthy growth of vegetation, it is important to obtain the chlorophyll content quickly and nondestructively [3,4]. A portable chlorophyll instrument is used to measure a relative chlorophyll content, which has real-time, rapid, and non-destructive advantages [5].

At present, hyperspectral remote sensing technology has been widely studied and applied in agriculture, including spectral feature analysis of crop leaves or canopy, monitoring and inversion of some physiological and biochemical parameters in crops, crop identification and classification, pest monitoring, etc. [6,7,8]. This technology can quickly obtain the continuous spectral curve of crops, and its small difference can reflect different characteristics such as crop growth. The visible range band (400–780 nm) of the spectrum is the strong absorption band of pigment [9]. The change of visible spectrum waveform is closely related to the content of chlorophyll in leaves. Jin et al. analyzed the spectrum of rice leaves and the corresponding chlorophyll content and found that the sensitive bands related to the chlorophyll content of rice leaves were 450–686 and 750–780 nm [10]. Lu et al. analyzed the correlation between the spectrum of cherry leaves and chlorophyll content after making various changes [11]. Using stepwise linear regression analysis, it was found that the variable log(1/R741) was highly correlated with the chlorophyll of cherry leaves. Zhang et al. conducted a variety of typical changes in the original winter wheat spectrum and found that the spectral change data based on the second derivative R′′ can accurately estimate the chlorophyll content under low temperature stress [12]. In the range of red light, the research of red edge parameters is also the focus of many researchers. Bonham Carter et al. defined the red edge position as the wavelength value corresponding to the first-order differential maximum in the red band and then analyzed its relationship with leaf chlorophyll content in detail [13]. Yang Jie et al. compared the reflectance of any two bands in the spectrum of rice leaves from 350 to 2500 nm and calculated its normalization index [14]. They proposed that the band ratio SR(R724, R709) and normalization index ND(R780, R709) are the two spectral indices most closely related to the chlorophyll content of rice leaves, and the determination coefficients are above 0.9. To extract sensitive bands, Wang et al. employed the elastic net approach to minimize the dimensionality of hyperspectral data and then retrieved the chlorophyll content of winter wheat [15]. Qiu et al. applied the SPAD value and spectral techniques to study the change of nitrogen during rape growth [16].

Because the spectral data obtained by the instrument has a certain noise, most researchers will preprocess the spectral data in the estimation of chlorophyll content of winter wheat [10,11,12,13,14]. However, single or two or three kinds of preprocessed spectral data or some spectral indices are generally used as a model input to estimate winter wheat chlorophyll content, and different preprocessing methods are used in different studies [11,12,14]. Few studies compare the effects of these common preprocessing or spectral indices on the results of a winter wheat leaf green content estimation model. Therefore, it is necessary to select some common preprocessed spectral data and select some spectral indices with high correlation with chlorophyll content as input values, and compare and analyze the model accuracy under various input values. In addition, for the remote sensing monitoring of winter wheat chlorophyll content, most researchers perform research based on the sample data of a certain growth period [17], which lacks universality for all growth periods. Therefore, it is necessary to consider the whole growth period of winter wheat and find a chlorophyll estimation model suitable for the whole growth period.

Therefore, this study will collect the spectral data of Winter Wheat in multiple growth stages (from jointing stage to maturity stage), take different combinations of preprocessed spectral data and spectral indices data [18] as input values, respectively, and model to estimate the SPAD value. In addition, PLSR [19,20] will be used to compare and analyze the estimation results of different models and explore the influencing factors of model accuracy and stability. It has certain application value for estimating the SPAD value in different growth stages and provides a theoretical basis and data preprocessing reference for estimating the chlorophyll content of vegetation from spaceborne hyperspectral satellite images.

2. Experiments and Methods

2.1. Study Area

The study area is located in the international agricultural high tech Industrial Park of Chinese Academy of Agricultural Sciences in Langfang City, Hebei Province. The geographical coordinates are 116°35′34″E–116°35′36″E and 39°35′50″N–39°35′53″N (Figure 1). The average annual temperature is 13.9 °C, and the average annual precipitation is 393.4 mm, belonging to the warm temperate continental monsoon climate. The total area of the test area is 1200 m² (20 m wide and 60 m long). The soil texture is mainly loamy, and the soil types are mainly brown soil, moisture soil and cinnamon soil, with a unit weight of 1.5 g/cm³. The winter wheat variety selected in the experiment is Jingdong 12, and the fertilization level is consistent with the field fertilization level in this area (pure nitrogen (N) 256.5 kg·hm⁻², phosphorus pentoxide (P₂O₅) 240 kg·hm⁻², all input at one time during sowing).

2.2. Spectral and SPAD Value Data Acquisition

The data used in the study mainly include the spectral data of winter wheat leaves at various growth stages and the corresponding SPAD value.

The spectral data of winter wheat leaves were measured by portable ground object spectrometer ASD FieldSpec4. The wavelength range of the spectrometer is 350–2500 nm, the spectral sampling interval is 1.4 nm (350–1000 nm), 2 nm (1001–2500 nm) and the spectral resolution is 3 nm (700 nm), 8 nm (1400, 2100 nm). The spectra of winter wheat leaves were measured from 10:30 to 13:30 Beijing time when the weather was sunny, cloudless or light cumulus, windless or wind speed lower than 1 m/s. Before measurement, the optical fiber probe is vertically aligned with the standard reference plate (whiteboard) for calibration. The winter wheat spectrum measurement is re-calibrated with the whiteboard every 15 min to prevent the influence caused by the drift of the sensor response system and the change of the solar incidence angle [21]. During the measurement, the measurer was dressed in dark color, facing the vertical direction of the sun (perpendicular to the main plane direction), holding a pistol, and the optical fiber probe was vertically pointing downward at the no shadow in the front leaf of the top leaf of winter wheat. The spectral measurement position of winter wheat was selected at the place with less stem veins and more mesophyll. The vertical distance between the optical fiber probe and the blade is 1 cm. The spectral curves of each leaf sample are measured repeatedly, and 5 spectral curves are collected, and the average value of the 5 spectral curves is taken as the final spectral reflectance of the sample. The spectrum of green vegetation is mainly affected by pigment content in the range of 400–900 nm, and it will show obvious peak and valley characteristics, which is a representative band range distinguished from non-green vegetation [22]. The study only makes correlation analysis on the spectral data in the range of 400–900 nm. The SPAD value was measured by portable chlorophyll meter SPAD-502 and replaced by a SPAD value. After the leaf spectrum is measured, a portable chlorophyll meter is used to evenly measure five values at the spectral measurement points immediately and the average value is calculated as the SPAD value sample. Each growth stage was randomly sampled in the experimental area.

Spectral data and SPAD data were collected at the jointing stage, heading stage, flowering stage, grain filling stage, milk ripening stage and mature stage. The data of the whole growth period include the data of six single-growth periods. The set aside method is used to divide the training set and the verification set, in which 4/5 of the samples are used for training, and the remaining 1/5 are reserved for verification. In order to make the types of samples in the training set and the verification set as balanced as possible, the samples in each growth period are sorted from small to large according to the SPAD value, and then, one sample from every four is taken into the verification set according to the approximate ratio of 4:1 between the training set and the verification set, and the remaining samples are put into the training set. The data set size and SPAD value information of each growth period are shown in

Table 1. The introduction of winter wheat sample sets on each growth stages.

Growth Stages	Data Collection Data	Sample Set	Number of Samples	SPAD Value
				Maximum	Minimum	Average	Standard Deviation
Jointing stage	26 April 2019	Training set	132	55.5	25.2	43.645	5.632
		Validation set	32	56.8	35.5	46.350	5.481
		Total sample set	164	56.8	25.2	44.173	5.722
Heading stage	9 May 2019	Training set	156	67.2	45.9	54.341	3.511
		Validation set	44	68.9	49.7	55.823	3.652
		Total sample set	200	68.9	45.9	54.667	3.604
Flowering stage	13 May 2019	Training set	78	60.7	46.4	53.304	2.652
		Validation set	20	65.1	51.7	56.585	3.196
		Total sample set	98	65.1	46.4	53.973	3.087
Filling stage	22 May 2019	Training set	156	70.1	46.6	55.112	3.187
		Validation set	39	61.4	43.8	54.754	3.133
		Total sample set	195	70.1	43.8	55.041	3.180
Milk ripening stage	28 May 2019	Training set	156	65.3	27.0	50.796	6.558
		Validation set	44	62	17.3	49.584	8.125
		Total sample set	200	65.3	17.3	50.529	6.969
Maturity stage	31 May 2019	Training set	156	63.6	3.2	43.013	12.580
		Validation set	39	58	2.5	42.236	13.099
		Total sample set	195	63.6	2.5	42.857	12.722
Whole growth stage		Training set	842	76.8	17.3	51.702	6.432
		Validation set	210	63.6	2.5	43.578	12.592
		Total sample set	1052	76.8	2.5	50.079	8.694

.

2.3. Spectral Index Collection

Affected by pigments, plant leaves have strong absorption characteristics in visible light band, especially in red band, and strong reflection characteristics in near-infrared band, which is the physical basis of remote sensing monitoring of green plants [23]. Through the reflectivity value of each band of visible light and near infrared, different vegetation indices can be obtained by different combinations of derivative values. 62 spectral indices related to the inversion of plant chlorophyll content in the published literature were collected and sorted out (

Table 2. Spectral indices used to estimate the vegetation physiological and ecological parameters.

Number	Spectral Indices	Formula	Reference	Number	Spectral Indices	Formula	Reference
V1	NDVI	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{670}}{{{\displaystyle R}}_{800}+{{\displaystyle R}}_{670}}$	[24]	V2	CI	$\frac{{{\displaystyle R}}_{750}}{\left({{\displaystyle R}}_{700}-{{\displaystyle R}}_{710}\right)-1}$	[25]
V3	GI	$\frac{{{\displaystyle R}}_{554}}{{{\displaystyle R}}_{677}}$	[26]	V4	SIPI (680)	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{455}}{{{\displaystyle R}}_{800}{{\displaystyle -R}}_{680}}$	[27]
V5	VI(700)	$\frac{{{\displaystyle R}}_{700}-{{\displaystyle R}}_{670}}{{{\displaystyle R}}_{700}+{{\displaystyle R}}_{670}}$	[28]	V6	RDVI	$\frac{\left({{\displaystyle R}}_{800}-{{\displaystyle R}}_{670}\right)}{\sqrt{\left({{\displaystyle R}}_{800}+{{\displaystyle R}}_{670}\right)}}$	[29]
V7	SR	$\frac{{{\displaystyle R}}_{800}}{{{\displaystyle R}}_{680}}$	[30]	V8	SR2	$\frac{{{\displaystyle R}}_{700}}{{{\displaystyle R}}_{670}}$	[31]
V9	MNDVI8	$\frac{\left({{\displaystyle R}}_{755}-{{\displaystyle R}}_{730}\right)}{\left({{\displaystyle R}}_{755}+{{\displaystyle R}}_{730}\right)}$	[32]	V10	DPI	$\frac{{{\displaystyle D}}_{688}\ast {{\displaystyle D}}_{710}}{{{{\displaystyle D}}_{697}}^2}$	[33]
V11	D2-C	$\frac{{{\displaystyle D}}_{705}}{{{\displaystyle D}}_{722}}$	[33]	V12	D1-CF	$\frac{{{\displaystyle D}}_{730}}{{{\displaystyle D}}_{706}}$	[33]
V13	NDVI2-LS,Ca	$\frac{{{\displaystyle R}}_{750}-{{\displaystyle R}}_{705}}{{{\displaystyle R}}_{750}+{{\displaystyle R}}_{705}}$	[34]	V14	Gitelson-LS,CTotal	$\frac{1}{{{\displaystyle R}}_{700}}$	[35]
V15	Datt4-LS,C	$\frac{{{\displaystyle R}}_{754}}{{{\displaystyle R}}_{704}}$	[36]	V16	Datt1-LS,Cb	$\frac{{{\displaystyle R}}_{672}}{{{\displaystyle R}}_{550}}$	[37]
V17	SIPI	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{445}}{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{680}}$	[27]	V18	SR5	$\frac{{{\displaystyle R}}_{752}}{{{\displaystyle R}}_{690}}$	[38]
V19	SR3-LS,S	$\frac{{{\displaystyle R}}_{440}}{{{\displaystyle R}}_{690}}$	[39]	V20	Vogelmann-LS,C	$\frac{{{\displaystyle R}}_{740}}{{{\displaystyle R}}_{720}}$	[40]
V21	Boochs1	${{\displaystyle D}}_{703}$	[41]	V22	Boochs2	${{\displaystyle D}}_{720}$	[41]
V23	SOFDR (625–795)	${\displaystyle {\sum }_{625}^{795}D}$	[42]	V24	CI	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{550}}{{{\displaystyle R}}_{800}}$	[43]
V25	MSR	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{445}}{{{\displaystyle R}}_{680}-{{\displaystyle R}}_{445}}$	[44]	V26	REP	$Max\left({{\displaystyle D}}_{680}{{\displaystyle ,D}}_{760}\right)$	[45]
V27	BGI	$\frac{{{\displaystyle R}}_{450}}{{{\displaystyle R}}_{550}}$	[46]	V28	SIPI (705)	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{455}}{{{\displaystyle R}}_{800}+{{\displaystyle R}}_{705}}$	[47]
V29	ZM	$\frac{{{\displaystyle R}}_{750}}{{{\displaystyle R}}_{710}}$	[46]	V30	Datt-LS,C	$\frac{{{\displaystyle R}}_{850}-{{\displaystyle R}}_{710}}{{{\displaystyle R}}_{850}-{{\displaystyle R}}_{680}}$	[36]
V31	SR6	$\frac{{{\displaystyle R}}_{750}}{{{\displaystyle R}}_{550}}$	[38]	V32	MNDVI1	$\frac{{{\displaystyle R}}_{755}-{{\displaystyle R}}_{745}}{{{\displaystyle R}}_{755}+{{\displaystyle R}}_{745}}$	[32]
V33	D690_red	${{\displaystyle D}}_{690}$	[47]	V34	NDVI3	$\frac{{{\displaystyle R}}_{682}-{{\displaystyle R}}_{553}}{{{\displaystyle R}}_{682}+{{\displaystyle R}}_{553}}$	[48]
V35	Maccioni-LS,C	$\frac{{{\displaystyle R}}_{780}-{{\displaystyle R}}_{710}}{{{\displaystyle R}}_{780}-{{\displaystyle R}}_{680}}$	[49]	V36	MTCI	$\frac{{{\displaystyle R}}_{754}-{{\displaystyle R}}_{709}}{{{\displaystyle R}}_{709}-{{\displaystyle R}}_{681}}$	[50]
V37	NPCI	$\frac{{{\displaystyle R}}_{680}-{{\displaystyle R}}_{430}}{{{\displaystyle R}}_{680}+{{\displaystyle R}}_{430}}$	[27]	V38	GNDVI-Ca	$\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{550}}{{{\displaystyle R}}_{800}+{{\displaystyle R}}_{550}}$	[51]
V39	Datt3-LS,C	$\frac{{{\displaystyle R}}_{850}}{{{\displaystyle R}}_{710}}$	[36]	V40	Datt5-LS,Ca,total	$\frac{{{\displaystyle R}}_{672}}{{{\displaystyle R}}_{550}\ast {{\displaystyle R}}_{708}}$	[36]
V41	Datt2-LS	$\frac{{{\displaystyle R}}_{860}}{{{\displaystyle R}}_{550}\ast {{\displaystyle R}}_{708}}$	[37]	V42	SR4	$\frac{{{\displaystyle R}}_{750}}{{{\displaystyle R}}_{700}}$	[38]
V43	SR1-LS,Ca	$\frac{{{\displaystyle R}}_{675}}{{{\displaystyle R}}_{700}}$	[52]	V44	SRPI	$\frac{{{\displaystyle R}}_{430}}{{{\displaystyle R}}_{680}}$	[27]
V45	Vogelmann2-LS,C	$\frac{{{\displaystyle R}}_{715}}{{{\displaystyle R}}_{705}}$	[40]	V46	Vogelmann3-LS,C	$\frac{{{\displaystyle R}}_{734}-{{\displaystyle R}}_{747}}{{{\displaystyle R}}_{715}+{{\displaystyle R}}_{726}}$	[40]
V47	SOFDR (680–780)	${\displaystyle {\sum }_{680}^{780}D}$	[45]	V48	Carter-I	$\frac{{{\displaystyle R}}_{695}}{{{\displaystyle R}}_{760}}$	[53]
V49	DVI	${{\displaystyle R}}_{800}-{{\displaystyle R}}_{670}$	[30]	V50	PSSRC	$\frac{{{\displaystyle R}}_{800}}{{{\displaystyle R}}_{680}}+\frac{{{\displaystyle R}}_{800}}{{{\displaystyle R}}_{635}}$	[54]
V51	Gitelson-RG	$\frac{{{\displaystyle R}}_{800}}{{{\displaystyle R}}_{550}}-1$	[55]	V52	BI	${{\displaystyle R}}_{800}{{\displaystyle +R}}_{670}+\frac{{{\displaystyle R}}_{550}}{\sqrt{3}}$	[43]
V53	TCARI	$3\ast \left(\left({{\displaystyle R}}_{700}-{{\displaystyle R}}_{670}\right)-0.2\ast \left({{\displaystyle R}}_{700}-{{\displaystyle R}}_{550}\right)\ast \left(\frac{{{\displaystyle R}}_{700}}{{{\displaystyle R}}_{670}}\right)\right)$					[56]
V54	MCARI1	$1.2\ast \left[2.5\ast \left({{\displaystyle R}}_{800}-{{\displaystyle R}}_{670}\right)-1.3\ast \left({{\displaystyle R}}_{800}-{{\displaystyle R}}_{550}\right)\right]$					[57]
V55	MCARI	$\frac{\left[\left({{\displaystyle R}}_{700}-{{\displaystyle R}}_{670}\right)-0.2\ast \left({{\displaystyle R}}_{700}-{{\displaystyle R}}_{550}\right)\right]}{\left(\raisebox{1ex}{${{\displaystyle R}}_{700}$}\!\left/ \!\raisebox{-1ex}{${{\displaystyle R}}_{670}$}\right.\right)}$					[58]
V56	TVI	$0.5\ast \left[120\ast \left({{\displaystyle R}}_{750}-{{\displaystyle R}}_{550}\right)-200\ast \left({{\displaystyle R}}_{670}-{{\displaystyle R}}_{550}\right)\right]$					[59]
V57	MCARI2	$\frac{1.5\ast \left[2.5\ast \left({{\displaystyle R}}_{800}-{{\displaystyle R}}_{670}\right)\right]-1.3\ast \left({{\displaystyle R}}_{800}-{{\displaystyle R}}_{550}\right)}{\sqrt{\left(2\ast {{\displaystyle R}}_{800}+1\right)-\left(6\ast {{\displaystyle R}}_{800}-5\ast \sqrt{{{\displaystyle R}}_{670}}\right)-0.5}}$					[57]
V58	EVI	$2.5\ast \left(\frac{{{\displaystyle R}}_{800}-{{\displaystyle R}}_{670}}{{{\displaystyle R}}_{800}-\left(6\ast {{\displaystyle R}}_{670}\right)-\left(7.5\ast {{\displaystyle R}}_{475}\right)+1}\right)$					[60]
V59	TCARI2-Wu	$3\ast \left(\left({{\displaystyle R}}_{750}-{{\displaystyle R}}_{705}\right)-0.2\ast \left({{\displaystyle R}}_{750}-{{\displaystyle R}}_{550}\right)\ast \left(\frac{{{\displaystyle R}}_{750}}{{{\displaystyle R}}_{705}}\right)\right)$					[61]
V60	DD	$\left({{\displaystyle R}}_{749}-{{\displaystyle R}}_{720}\right)-\left({{\displaystyle R}}_{701}-{{\displaystyle R}}_{672}\right)$					[62]
V61	MND (705)	$\frac{\left({{\displaystyle R}}_{750}-{{\displaystyle R}}_{705}\right)}{\left({{\displaystyle R}}_{750}+{{\displaystyle R}}_{705}-2{{\displaystyle R}}_{445}\right)}$					[44]
V62	MNDVI	$\frac{\left({{\displaystyle R}}_{800}-{{\displaystyle R}}_{680}\right)}{({{\displaystyle R}}_{800}+{{\displaystyle R}}_{680}-2{{\displaystyle R}}_{445})}$					[36]

). By analyzing the correlation between these spectral indices and the SPAD value, the sensitive spectral indices set will be selected to predict the SPAD value of winter wheat.

2.4. Spectral Preprocessing Methods

Denoising, data form transformation and dimension reduction single preprocessing were applied to the original winter wheat spectral data in turn (

Table 3. Combination pretreatment.

Preprocessing	Name
Denoising	ND, WPD
Data form transformation	R, R’, (1/R)’, 1/R, log(R)
dimension reduction	NDR, PCADR

). Two different denoising approaches are no denoising (ND) and wavelet packet denoising (WPD) [63,64,65]. Five different mathematical forms of transformation are the original spectral reflectance data R, reciprocal 1/R, log(R), first derivative R’ and reciprocal first derivative (1/R)’ [66]. Two different dimensionality reduction approaches are no dimension reduction (NDR) and principle component analysis dimension reduction (PCADR) [67,68,69,70].

Denoising, data form transformation, and dimension reduction single preprocessing are combined to form a total of 20 combined preprocessing methods. The model’s input value is various combinations of preprocessed spectral data, and the model estimation is established by PLSR.

2.5. Partial Least Squares Regression

The link between vegetation spectrum and vegetation chlorophyll concentration can be studied using partial least squares regression (PLSR). This method can estimate the dependent variable through the linear combination of independent variables [71]. It is a multiple independent variables to multiple dependent variables linear regression modeling technique. When the sample size is small and there are multiple correlations between variables, the PLSR method has more advantages than the traditional regression model [71]. Due to the possible strong correlation between independent variables, it is easy to lead to overfitting of the problem when solving the linear regression problem of multiple independent variables to multiple dependent variables. However, the PLSR technique will identify several linear independent new variables to substitute the previous independent variables, allowing the diversity between independent variables to be maximized and the overfitting problem to be alleviated.

In this paper, the preprocessed spectral data and the sensitive vegetation indices with high correlation with winter wheat chlorophyll are used as the input values of the model, and the PLSR method is used to estimate and analyze the SPAD value of winter wheat.

2.6. Model Performance Evaluation Indices

The root mean square error of the training set (RMSE_T), the root mean square error of the validation set (RMSE_V), the determination coefficient of the training set R²_T, the determination coefficient of the verification set R²_V, and the ratio of performance to deviation (RPD) were all used to carefully consider the model’s effectiveness in the research.

The determination coefficient R² is the second power of the correlation coefficient R. The calculation formula of the correlation coefficient R is shown in Formula (1).

$${{\displaystyle R}}_i=\frac{\mathrm{cov}\left(x,y\right)}{\sqrt{D\left(x\right)}\sqrt{D\left(y\right)}}=\frac{{\displaystyle \sum _{n=1}^N\left(x_{ni}-\overline{x_i}\right)\left(y_n-\overline{y}\right)}}{\sqrt{{\displaystyle \sum _{n=1}^N{\left(x_{ni}-\overline{x_i}\right)}^2{\displaystyle \sum _{n=1}^N{\left(y_n-\overline{y}\right)}^2}}}}$$

(1)

In Formula (1), the R_i is the correlation coefficient between the winter wheat leaf spectral reflectance in band i and the winter wheat leaf SPAD value, N is the total number of samples, x_ni is the spectral reflectance of winter wheat leaves in band i of the nth sample, $\overline{x_i}$ is the average spectral reflectance of winter wheat leaves in band i of all samples, y_n is the SPAD value of winter wheat leaves in the nth sample, and $\overline{y}$ is the average SPAD value of winter wheat leaves in all samples. The value of determination coefficient is equal to R².

The calculation formula of root mean square error (RMSE) is shown in Formula (2).

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{n=1}^N{\left(y_{nt}-y_{np}\right)}^2}}{N}}$$

(2)

In Formula (2), RMSE is root mean square error, N is the total number of samples, y_nt is the measured value of winter wheat leaf SPAD value, y_np is the estimated value of winter wheat leaf SPAD value.

The calculation formula of RPD is shown in Formula (3).

RPD = SD/RMSE_V

(3)

In Formula (3), RPD is the ratio of performance to deviation, SD is the standard deviation of SPAD value of winter wheat leaves in the validation set.

Generally speaking, the higher the value of the R², the higher the correlation between the predicted value and the real value. The RMSE value should be as low as possible. The stronger the model’s stability, the closer the RMSE_T and RMSE_V are. RPD can be categorized into three categories: The model is useful for accurately predicting the SPAD value of winter wheat when RPD is equal to or greater than 2.0. The model’s reliability can be enhanced by fine-tuning when the RPD is below 2.0. The model is unstable when RPD is equal or falls below 1.4 [72].

3. Result

3.1. Sensitive Spectral Indices Screening

By analyzing the correlation between these spectral indices and SPAD value, the sensitive spectral indices set was selected to predict the SPAD value of winter wheat.

Figure 2 shows the changes of 62 spectral indices and correlation coefficient of leaf SPAD value in jointing, heading, flowering, filling, milk maturity, maturity and whole growth stage of winter wheat. Each vertical line in the figure corresponds to a spectral index. The seven points on the vertical line represent six single growth periods and whole growth periods. The length of the vertical line is the maximum and minimum difference between spectral index and correlation coefficient of chlorophyll concentration in six single growth periods and whole growth periods. The association between each spectral index and SPAD value is more or less affected by different growth periods, as seen in the figure. The association between spectral index V11 and chlorophyll concentration at heading stage is −0.11594, but the association between spectral index V11 and leaf SPAD value at maturity stage is as high as −0.919, which fluctuates greatly. We found that the vertical line length corresponding to each spectral index ranges from 0.1 to 1.1. The sensitive spectral indices selected by comprehensive consideration can reflect the differences of different growth periods, and it is applicable to all growth periods. It is based on the spectral indices corresponding to the maximum value of positive correlation coefficient and the minimum value of negative correlation coefficient between each growth period and SPAD value, to screen the sensitive spectral indices.

Table 4. Sensitive spectral indices.

Growth Stages	Highest Positive Correlation Spectral Indices	Highest Positive Correlation Coefficient	Lowest Negative Correlation Spectral Indices	Lowest Negative Correlation Coefficient
Jointing stage	V7	0.795	V26	−0.742
Heading stage	V24	0.415	V42	−0.400
Flowering stage	V25	0.553	V35	−0.521
Filling stage	V27	0.413	V35	−0.380
Milk ripening stage	V49	0.720	V26	−0.717
Maturity stage	V13	0.919	V8	−0.919
Whole growth stage	V50	0.830	V8	−0.799

lists the spectral indices and correlation coefficients corresponding to the maximum positive correlation coefficient and the minimum negative correlation coefficient of the SPAD value in different growth periods. The maximum positive and negative correlation coefficients at jointing, milk maturity, maturity and whole growth stages are higher, above ±0.7, but the maximum positive and negative correlation coefficients at heading and filling are slightly smaller, basically below ±0.5. According to Table 3, 11 spectral indices V7, V8, V13, V24, V25, V26, V27, V35, V42, V49 and V50 are finally selected as sensitive spectral indices. The bands involved in these sensitive spectral indices are basically in the range of 670–755 nm, which are concentrated near the red edge, and some spectral indices also involve the 550 nm green peak band. This shows that the SPAD value has a great correlation with the red edge information and green peak information. The hyperspectral differences of winter wheat leaves at various growth stages are also mainly reflected in the vicinity around the green peak and red edge.

3.2. Estimation of SPAD Value Based on Sensitive Spectral Indices Set

The value range of each sensitive spectral index is quite different. In the first place, the normalized spectral indices are employed as the input value of the PLSR model to complete the subsequent SPAD value estimation.

Table 5. Estimation results of chlorophyll concentration in various growth stages with spectral indices set as input value.

Growth Stages	RMSET (SPAD)	RMSEV (SPAD)	RPD	R2T	R2V
Jointing stage	3.204	3.473	1.578	0.687	0.706
Heading stage	2.906	3.894	0.938	0.319	0.010
Flowering stage	2.215	3.609	0.885	0.310	0.002
Filling stage	2.646	3.214	0.975	0.315	0.063
Milk ripening stage	4.422	5.136	1.582	0.552	0.634
Maturity stage	4.517	3.624	3.615	0.882	0.974
Whole growth stage	3.894	6.399	1.956	0.634	0.792

shows the estimated findings of PLSR chlorophyll concentration for each growth period. Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 demonstrate a scatter diagram of the estimation results of the SPAD value in various growth phases, in which figure (a) is the estimation results of training set and figure (b) is the estimation results of the validation set. The results showed that the estimation results of the heading stage, flowering stage and filling stage were poor, with RPD value less than 1.4 and R²_V value less than 0.1. The estimation results of the jointing stage and milk ripening stage were better, RPD value was greater than 1.5 and R²_V value was greater than 0.6. The estimation results of the mature stage and whole growth stage are the best, RPD value is basically above 2, and especially in the mature stage, the R²_V value was up to 0.974.

3.3. Estimation of SPAD Value Based on Different Pretreatment Approaches

There are great differences between the estimated results of the preprocessed spectral data model in different growth stages.

Table 6. The optimal estimation results under the data preprocessing of each growth stages.

Growth Stages	Pretreatment Method	RMSET (SPAD)	RMSEV (SPAD)	RPD	R2T	R2V	R2V Growth Value	RPD Growth Value
Jointing	WPD-(1/R)’-PCADR	3.377	3.453	1.587	0.650	0.734	0.318	0.578
Heading	WPD-1/R-PCADR	2.616	3.532	1.034	0.450	0.180	0.178	0.405
Flowering	WPD-(1/R)’-PCADR	0.545	3.948	0.809	0.983	0.092	0.071	0.220
Filling	ND-(1/R)’-PCADR	2.777	2.616	1.198	0.244	0.340	0.330	0.225
Milk ripening	WPD-(1/R)’-PCADR	4.881	6.266	1.297	0.452	0.512	0.005	0.101
Maturity	WPD-R’-PCADR	4.143	3.734	3.508	0.903	0.970	0.109	1.170
Whole growth	WPD-R’-PCADR	2.844	6.107	2.062	0.806	0.785	0.044	0.180

lists the best model’s estimation findings under 20 kinds of combined pretreatments in different growth periods. Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 are scatter plots of the estimation results of the preprocessing optimal model in six single growth stages, as well as the entire growth stage. R²_V growth value and RDP growth value in Table 6 refer to the growth values of R²_V and RDP, respectively, compared with the model estimation results of the original spectral data.

Table 6 and Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 demonstrate that the chlorophyll estimation results of the optimal model in different growth periods are basically obtained by preprocessing WPD-R’-PCADR or WPD-(1/R)-PCADR, and the R²_V value can be up to 0.970, indicating that the combination of WPD denoising, PCA dimensionality reduction and first derivative mathematical form transformation can well increase the PLSR SPAD value estimate model’s accuracy. This is because the first derivative transformation can highlight useful information, denoising can decrease the noise in the original spectral information, and dimensionality reduction can better select useful information and avoid overfitting in model training due to data redundancy. In addition, the chart also shows that the RPD value in the maturity stage and the whole growth stage is greater than 2, and the model R²_V value is above 0.75; especially in the mature stage, the R²_V value was up to 0.97, which can be a good estimate of the SPAD value of winter wheat. The RPD value of jointing stage is greater than 1.4, which can also better estimate the SPAD value of winter wheat. However, the estimation results of the SPAD value in the heading stage, flowering stage, filling stage and milk maturity stage were extremely poor, R²_V was less than 0.4, and the corresponding RPD value was less than 1.4.

3.4. Comparison of SPAD Value Estimation Results of Different Model Inputs

Taking the sensitive spectral indices or the preprocessed spectral data as the model input value, the estimation results have some similarities, which are mainly reflected in different growth periods.

Firstly, the estimation accuracy of the mature stage and whole growth stage is very high, RPD value is greater than 2, and R²_V can be up to 0.97 in the mature stage. The estimation accuracy of the jointing stage and milk maturity stage is relatively high, RPD value is basically greater than 1.4, and the accuracy R²_V value is also greater than 0.5. The model’s accuracy in predicting the stages of heading, flowering, and filling are relatively poor, R²_V value is less than 0.4, and the estimation results are obviously underfitted (Table 5 and Table 6). The estimation accuracy of different growth periods varies widely, and one of the influencing factors is the original sample set. The number of samples collected in every growth period is similar; however, the STD_chl in the sample set is substantially different (Table 1). From the turning green to jointing and then to the heading stage, the temperature increases continuously, the winter wheat leaves grow continuously, and the top leaf size also increases continuously. During this period, the chlorophyll content increases sharply. From filling to the mature stage, the grain in the wheat ear takes shape, its reproductive growth is dominant, and the vegetative organs such as leaves gradually stop growing and begin to wither and fall off. Coupled with the damage of high temperature to leaf cells, the chlorophyll content in the leaves decreases significantly. Therefore, the sample’s SPAD value measured in these two periods has a large range, and the STD_chl in the sample set is also large. The standard deviation of the SPAD value in the sample set at the jointing stage, milk maturity stage, maturity stage and whole growth stage is greater than 5.5. From heading stage to filling stage, the number and size of leaves basically did not change, and the chlorophyll content increased slowly. Therefore, the range of SPAD value in the sample set measured during the growth period is small, and the STD_chl in the sample set is also small. The standard deviation of the SPAD value in the heading, flowering and filling stage is less than 4.

Secondly, using preprocessed spectral data or sensitive spectral indices set as the model input value can significantly boost the precision and stability of the PLSR-based SPAD value estimating model, and when the STD_chl of all samples in the model sample set is greater than 5.5 (Table 1, Table 5 and Table 6), the estimation accuracy is higher (the estimation accuracy is greater than 0.5), and the model is stable (RPD is greater than 1.4). Moreover, when STD_chl in the sample set is greater than 5.5, the larger the SPAD value in the sample set, the more accurate the model’s estimation. Most important of all, the STD_chl in the sample set and the estimation accuracy of the model from high to low are the mature stage, whole growth stage, jointing stage and milk mature stage. It can be seen that the SPAD value estimation model based on PLSR is particularly responsive to the input sample set’s STD_chl in addition to the high requirements for the spectral input value of the model (appropriate spectral data preprocessing or appropriate spectral indices set). In addition, there are great differences in the estimation results of single growth period data. If only the data of a single growth period are used to build a model to estimate the SPAD value, the universality of the estimation results is too weak. It is suggested to collect the data of mixed growth period (such as the whole growth period in this paper) for relevant estimation research, and the stability of the model is stronger.

The estimation results of input values of different models also have some differences. When the STD_chl in the input value sample set is greater than 6, taking the sensitive spectral indices as the input value is more accurate than taking the preprocessed spectral data. The calculation formula of spectral indices involves the mathematical form transformation of spectral data. Taking spectral indices as the model’s input value also has a certain function of data compression and dimensionality reduction. Therefore, the spectral indices set selected in this study can significantly aid in improving the model’s accuracy and reliability.

3.5. Estimation of SPAD Value with Different Chlorophyll Standard Deviations

For the sake of further confirming the estimation model’s sensitivity to the STD_chl in the input sample set, we estimated the SPAD value in different standard deviation sample sets. Within this investigation, the SPAD value in all samples ranges from 2.5 to 76.8. Taking 5 as the gradient and making statistics in the range of 0 to 80 (Figure 17), it is found that the SPAD value of most samples is concentrated in the range of 40 to 60. Based on the principle that the sample set has as many standard deviations (STD) of different SPAD values as possible, the sample set with different SPAD value ranges is set. The range of SPAD value in the sample set ranges from 5 to 80. The spectral data of each sample set pretreated by WPD-(1/R)-PCADR are used as the input value of the model, and the model estimation accuracy of different SPAD value ranges was analyzed using the PLSR SPAD value estimation model (

Table 7. The estimation results of different SPAD value ranges.

SPAD Value Range	STD (SPAD)	RMSET (SPAD)	RMSEV (SPAD)	RPD	R2T	R2V
50–55	1.393	1.299	1.305	1.065	0.133	0.121
50–60	2.424	2.159	2.265	1.083	0.203	0.151
45–60	3.462	2.641	2.653	1.301	0.420	0.422
45–65	3.748	3.018	3.070	1.223	0.352	0.338
40–65	4.981	3.271	3.657	1.362	0.57	0.472
40–80	5.173	3.644	3.699	1.378	0.509	0.485
35–80	5.878	3.664	3.694	1.578	0.614	0.607
30–80	6.242	4.096	4.065	1.523	0.573	0.576
25–80	6.803	4.469	4.365	1.544	0.572	0.592
15–55	7.197	4.500	4.565	1.534	0.616	0.589
15–80	7.664	3.689	4.748	1.603	0.771	0.626
00–80	8.680	4.161	4.841	1.774	0.773	0.697

).

The research shows that when the SPAD value range in the sample set is small (50~55, 50~60), the standard deviation of the sample set is also small, and the corresponding model R²_V value is also poor (R²_V is less than 0.2). As the range of SPAD values in the sample set gradually increases, the standard deviation also increases, and the corresponding model estimation accuracy (R²_V) basically shows a gradually increasing trend, and the more stable the model estimation result is (RPD). Figure 18 shows the variation law of RPD with the STD_chl in the sample set, and Figure 19 shows the variation law of R²_V with the STD_chl in the sample set. It can be seen from the two figures that the STD_chl in the sample set is highly correlated with the PLSR SPAD value estimation model’s accuracy and reliability. When the STD_chl in the sample set is larger than 5.5, RPD is greater than 1.4 and R²_V is higher than 0.5, the model is stable, and its accuracy is high. At this time, the PLSR model could be used to predict the SPAD value with high accuracy.

4. Discussion

4.1. Pretreatment Methods

In this study, common spectral preprocessing methods were compared, and it was found that using both sensitive spectral indices and preprocessed spectral data as model input values could increase the model’s estimation accuracy and reliability to some extent. This also illustrates the importance of spectral data preprocessing. In particular, it can be seen from Table 6 that, no matter in which growth stages, the model inversion accuracy was highest when the pretreatment method was WPD-R’-PCADR or WPD-(1/R)’-PCADR. When WPD and PCADR are used combined, the benefits of the derivative technique become clear. The derivative approach, according to Oldham et al. and Li et al., is not only a useful tool for studying spectral data, but it also aids in the resolution of multicollinearity issues [73,74]. As a result, it can be utilized to improve the analysis’s sensitivity. It also aids in the reduction of noise to some extent. The first derivative (FD) provides the reflectance spectrum’s slope, whereas the second derivative (SD) provides the reflectance spectrum’s slope change [74]. Although SD allows more absorption peaks to be separated, it also introduces noise and may lead to errors. Through SD and FD changes, the spectrum is severely deformed and leads to sharp peaks. For the pretreatment of spectral data, the fractional derivative can reduce the range of spectral variation to a certain extent and retain the form properties of the original spectrum as far as possible, which is more useful than the integer derivative (FD, SD). Fractional derivatives can really be utilized to include further valuable data coming from remote sensing by extending the order to non-integers, which could also add more details to the spectrum than integer derivatives. Only FD was employed to measure SPAD values in this research. Other higher-order integer and fractional derivatives will be used to preprocess spectral data in the future.

4.2. Influence of Sample Set on Model Accuracy

The results of this paper show that (Figure 18 and Figure 19) the STD_chl in the model input sample set is highly sensitive to the accuracy of the PLSR model in evaluating the SPAD value. This has to do with the characteristics of the PLSR method itself. PLSR is a machine learning algorithm, which has high requirements for the model input sample set. It needs the number of samples to be as large and diverse as possible. When the sample set is too small or the data range is too monotonous, it is easy to lead to the phenomenon of underfitting and overfitting, and the generalization ability of the model is weak. In this study, the STD_chl in the sample set is too small, which is the performance of poor sample diversity. The SPAD values in the heading stage, flowering stage and milk ripening stage are relatively concentrated due to their own physiological characteristics. The standard deviation of the SPAD value in the corresponding sample set is less than 4, and the accuracy of the corresponding model is also low. However, there are not enough data to prove whether the accuracy tends to be stable when the standard deviation is large to a certain value. More growth period data need to be collected for further verification.

Table 7 reveals that when the STD_chl in the sample set is greater than 5.5, the larger the STD_chl in the sample set, the higher the estimation accuracy of the model. Due to the small number of samples collected from the research, whether the threshold of 5.5 can be applied to other scenes needs to be further verified. In addition, based on the biological characteristics of winter wheat itself, the content of chlorophyll in leaves has a certain range. The STD_chl in the sample set we collected will always reach an upper limit. At this time, the relationship between the STD_chl and the accuracy of the model also needs to be further explored and verified. In following research, we will conduct deeper exploration, research and verification on the relationship between the sample set and model accuracy.

4.3. Universality of Data

Taking winter wheat as the research object and taking the hyperspectral data and corresponding SPAD value in different growth periods as the data source, this paper establishes a model by using the PLSR method to estimate the SPAD value and analyzes the estimation results in detail. The research has achieved some results, but the scope of the study area is small. When the variety of winter wheat changes or the growing environment changes, the research results need to be further analyzed and verified. In addition, it is relatively difficult to obtain data at the leaf scale of winter wheat, because it is susceptible to weather (when there are clouds and winds, etc.), and data collectors need certain professional experience. At present, in the quantitative remote sensing’s field, combining ground non-imaging spectral data with UAV imaging spectral data and satellite image multi-spectral data to realize multi-level and multi-scale crop growth monitoring is an unavoidable tendency. Wang et al. combined ground hyperspectral data with GF1 satellite multispectral images to achieve an inversion of chlorophyll concentration geographic variation in the winter wheat canopy [75]. In the subsequent study, we attempted to expand the research scope and conduct satellite-scale estimation of the winter wheat SPAD value, so as to analyze and find efficient and high-precision estimation methods for winter wheat chlorophyll that are suitable for more conditions.

5. Conclusions

Depending on the spectral data and SPAD value in various growth stages, taking the sensitive spectral indices and preprocessed spectral data as the model input values, the model was constructed by the PLSR method to estimate the SPAD value, and the estimated results were compared and analyzed in detail. The main conclusions are as follows:

(1)

The 11 spectral indices (V13, V15, V16, V17, V25, V39, V41, V42, V43, V47 and V57) selected in this paper can be used as the input values of the model, which could boost the model’s precision and reliability while calculating the SPAD value.

(2)

Compared with the original spectral data and preprocessed spectral data as the model’s input value, especially spectral data preprocessed by WPD-(1/R)-PCADR or WPD-R’-PCADR, it can increase the accuracy of the SPAD value estimation model and enhance the model’s stability.

(3)

When the STD_chl in the sample set is less than 4, the estimation results of the SPAD value are prone to underfitting; when the STD_chl in the sample set is greater than 5.5, the greater the STD_chl in the sample set, the higher the model’s estimating accuracy. In this case, the advantage of using sensitive spectral indices and preprocessing spectral dataset as model input values to increase the estimation model’s precision and stability is obvious. In addition, when the STD_chl in the sample set was greater than 6, the model with the sensitive spectral indices as the model input had a greater estimation accuracy than the model with the pretreatment spectral dataset.

(4)

When using the spectral data and corresponding SPAD value data of a single growth period as the data source, the estimation results were not representative when using the PLSR method to predict the SPAD value, and the universality of data related to other growth periods was poor. Modeling using data from the whole growth period can improve the universality ability and stability of the model. It is recommended that spectral data for the whole fertility period be used as the data source and that the STD_chl corresponding to the data source should be as large as possible (standard deviation of SPAD values > 5.5).