Gravity Wave Parameters and Their Seasonal Variations Study near 120°E China Based on Na LIDAR Observations
Abstract
:1. Introduction
2. Method
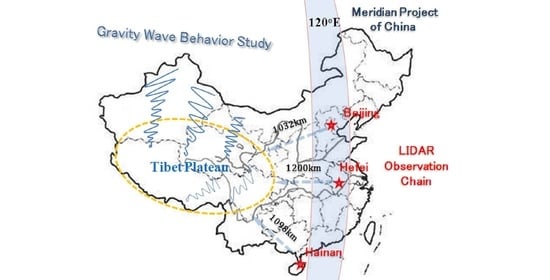
2.1. Instrumentations
2.2. Data and Analysis Method
3. Results
3.1. Study of Atmospheric Density Perturbations’ Vertical Wave Number Spectra
3.2. Study of Atmospheric Density Perturbations’ Temporal Frequency Spectra
3.3. GW Activity along the 120°E in China and Their Seasonal Variation Behaviors
3.3.1. Analyze GW Activity along 120°E in China and Their Seasonal Variation Studies
3.3.2. Analysis of GW Activity in Beijing and Hefei and Their Seasonal Variation Studies
3.3.3. Analysis of the Seasonal Variation of Gravity Wave Activity in Hainan
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alexander, M.; Pfister, L. Gravity wave momentum flux in the lower stratosphere over convection. Geophys. Res. Lett. 1995, 22, 2029–2032. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Gardner, C.S.; Voelz, D.Z. Lidar studies of the nighttime sodium layer over Urbana, Illinois, 2. Gravity waves. J. Geophys. Res. 1987, 92, 4673–4693. [Google Scholar] [CrossRef]
- Yang, G.; Clemesha, B.; Batista, P.; Simonich, D. Improvement in the technique to extract gravity wave parameters from lidar data. J. Geophys. Res. 2008, 113, D19111. [Google Scholar] [CrossRef]
- Yang, G.; Clemesha, B.; Batista, P.; Simonich, D. Lidar study of the characteristics of gravity waves in the mesopause region at a southern low-latitude location. J. Atmos. Sol. Terr. Phys. 2008, 70, 991–1011. [Google Scholar] [CrossRef]
- She, C.Y.; Yu, J.R.; Huang, J.W.; Nagasawa, C.; Gardner, C.S. Na temperature lidar measurements of gravity wave perturbations of wind, density and temperature in the mesopause region. Geophys. Res. Lett. 2012, 18, 1329–1331. [Google Scholar] [CrossRef]
- Yang, G.; Clemesha, B.; Batista, P.; Simonich, D. Gravity wave parameters and their seasonal variations derived from Na lidar observations at 23°S. J. Geophys. Res. 2006, 111, D21107. [Google Scholar] [CrossRef]
- Senft, D.C.; Gardner, C.S. Seasonal variability of gravity wave activity and spectra in the mesopause region at Urbana. J. Geophys. Res. 1991, 96, 17229–17264. [Google Scholar] [CrossRef]
- Xu, G.; Wan, W.; She, C.; Du, L. The relationship between ionospheric total electron content (TEC) over Ease Asia and the tropospheric circulation around the Qinghai-Tibet Plateau obtained with a partial correlation method. Adv. Space Res. 2008, 42, 219–223. [Google Scholar] [CrossRef]
- Wan, W.; Yuan, H.; Ning, B.; Liang, J.; Ding, F. Traveling ionospheric disturbances associated with the tropospheric vortexes around Qinghai-Tibet Plateau. Geophys. Res. Lett. 1998, 25, 3775–3778. [Google Scholar] [CrossRef]
- Wang, C. New Chains of Space Weather Monitoring Stations in China. Space Weather 2010, 8, S08001. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Peng, Z. Solar wind impacts on growth phase duration and substorm intensity: A statistical approach. J. Geophys. Res. 2013, 118, 4270–4278. [Google Scholar] [CrossRef]
- Sun, T.R.; Wang, C.; Wang, Y. Different Bz response regions in the nightside magnetosphere after the arrival of an interplanetary shock: Multipoint observations compared with MHD simulations. J. Geophys. Res. 2012, 117, A05227. [Google Scholar]
- Batista, P.P.; Clemesha, B.R.; Batista, I.S.; Simonich, D.M. Characteristics of the sporadic sodium layers observed at 23°S. J. Geophys. Res. 1989, 94, 15349–15358. [Google Scholar] [CrossRef]
- Gong, S.; Yang, G.; Dou, X.; Xu, J.; Chen, C.; Gong, S. Statistical study of atmospheric gravity waves in the mesopause region observed by a lidar chain in eastern china. J. Geophys. Res. Atmos. 2015, 120, 7619–7634. [Google Scholar] [CrossRef]
- Long, R.R. Some aspects of the flow of stratified fluids, III, Continuous density gradients. Tellus 1955, 7, 341–357. [Google Scholar] [CrossRef]
- Sato, K. Small-scale wind disturbances observed by the MU radar during the passage of typhoon Kelly. J. Atmos. Sci. 1993, 50, 518–537. [Google Scholar] [CrossRef]
- Sato, K. A statistical study of the structure, saturation and sources of inertio-gravity waves in the lower stratosphere observed with the MU radar. J. Atmos. Terr. Phys. 1994, 56, 755–774. [Google Scholar] [CrossRef]
- Zhang, S.D.; Yi, F. Latitudinal and seasonal variations of inertial gravity wave activity in the lower atmosphere over central China. J. Geophys. Res. 2007, 112, D05109. [Google Scholar] [CrossRef]
- Gong, S.H.; Yang, G.T.; Xu, J.Y.; Wang, J.H.; Guan, S.; Gong, W.; Fu, J. Statistical characteristics of atmospheric gravity wave in the mesopause region observed with a sodium lidar at Beijing, China. J. Atmos. Sol. Terr. Phys. 2013, 97, 143–151. [Google Scholar] [CrossRef]
- Lee, D.Y.; Ahn, J.B.; Yoo, J.H. Climate dynamics Enhancement of seasonal prediction of East Asian summer rainfall related to western tropical Pacific convection. Clim. Dyn. 2015, 45, 1025–1042. [Google Scholar] [CrossRef] [Green Version]
- Huang, R.; Sun, F. Impacts of the tropical western Pacific on the East Asia summer monsoon. J. Meteorol. Soc. Jpn. 1992, 70, 243–256. [Google Scholar] [CrossRef]
- Huang, G. An index measuring the interannual variation of the East Asian summer monsoon—The EAP index. Adv. Atmos. Sci. 2004, 21, 41–52. [Google Scholar] [CrossRef]
- Lee, S.S.; Lee, J.Y.; Ha, K.J.; Wang, B.; Schemm, J. Deficiencies and possibilities for long-lead coupled climate prediction of the western North Pacific-East Asian summer monsoon. Clim. Dyn. 2011, 36, 1173–1188. [Google Scholar] [CrossRef]
- Li, C.; Lu, R.; Dong, B. Predictability of the western North Pacific summer climate demonstrated by the coupled models of ensembles. Clim. Dyn. 2012, 39, 329–346. [Google Scholar] [CrossRef]
- Alexander, M.J.; Gille, J.; Cavanaugh, C.; Coffey, M.; Craig, C.; Eden, T.; Francis, G.; Halvorson, C.; Hannigan, J.; Khosravi, R.; et al. Global estimates of gravity wave momentum flux from High Resolution Dynamics Limb Sounder observations. J. Geophys. Res. 2008, 113, D15S18. [Google Scholar]
- Wright, C.J.; Gille, J.C. HIRDLS observations of gravity wave momentum fluxes over the monsoon regions. J. Geophys. Res. 2011, 116, D12103. [Google Scholar] [CrossRef]
- Li, Q.; Xu, J.; Liu, X.; Yuan, W.; Chen, J. Characteristics of mesospheric gravity waves over the southeastern Tibetan Plateau region. J. Geophys. Res. 2016, 121, 9204–9221. [Google Scholar] [CrossRef]
- Beatty, T.J.; Hostetler, C.A.; Gardner, C.S. Lidar observations of gravity wave and their spectra near the mesopause and stratopause at Arecibo. J. Atoms. Sci. 1992, 49, 477–496. [Google Scholar] [CrossRef]
- Collins, R.L.; Nomura, A.; Gardner, C.S. Gravity waves in the upper mesosphere over Antarctica: Lidar observations at the South Pole and Syowa. Geophys. Res. Lett. 1994, 99, 5475–5485. [Google Scholar] [CrossRef]
- Dewan, E.M.; Good, R.E. Saturation and the ‘‘universal spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res. 1986, 91, 2742–2748. [Google Scholar] [CrossRef]
- Dewan, E.M. The saturated-cascade model for atmospheric gravity wave spectra and the wavelength-period (W-P) relations. Geophys. Res. Lett. 1994, 21, 817–820. [Google Scholar] [CrossRef]
- Hines, C.O. The saturation of gravity waves in the middle atmo-sphere, part22. Development of Doppler-spread theory. J. Atmos. Sci. 1991, 48, 1360–1379. [Google Scholar]
- Tsuda, T.; Inoue, T.; Fritts, D.C.; Vanzandt, T.E.; Kato, S.; Sato, T.; Fukao, S. MST radar observations of a saturated gravity wave spectrum. J. Atmos. Sci. 1989, 46, 2440–2447. [Google Scholar] [CrossRef]








| Transmitter | Nd: YAG Laser | DYE Laser |
|---|---|---|
| Wavelength | 532 nm | 589 nm |
| Pulse energy | 400 mJ | 40 mJ |
| Repetition rate | 30 Hz | 30 Hz |
| Pulse width | 10 ns | 10 ns |
| Beam divergence | <0.5 mrad | <0.5 mrad |
| Receiver | ||
| Telescope aperture | 1 m | |
| Field of view | 1 mrad | |
| Bandwidth | 1.0 nm | |
| Data acquisition | ||
| MCS-pci count rate | 150 MHz | |
| Bin width | 640 ns |
| Hainan | Beijing | Hefei | |
|---|---|---|---|
| Distance to wave source (km) | 1098 | 1132 | 1200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, X.; Yang, G.; Batista, P.P.; Wang, J.; Andrioli, V.F.; Cheng, X.; Jiao, J.; Du, L.; Zhang, T.; Yang, H.; et al. Gravity Wave Parameters and Their Seasonal Variations Study near 120°E China Based on Na LIDAR Observations. Remote Sens. 2022, 14, 4798. https://doi.org/10.3390/rs14194798
Zou X, Yang G, Batista PP, Wang J, Andrioli VF, Cheng X, Jiao J, Du L, Zhang T, Yang H, et al. Gravity Wave Parameters and Their Seasonal Variations Study near 120°E China Based on Na LIDAR Observations. Remote Sensing. 2022; 14(19):4798. https://doi.org/10.3390/rs14194798
Chicago/Turabian StyleZou, Xu, Guotao Yang, Paulo Prado Batista, Jihong Wang, Vania F. Andrioli, Xuewu Cheng, Jing Jiao, Lifang Du, Tiemin Zhang, Hong Yang, and et al. 2022. "Gravity Wave Parameters and Their Seasonal Variations Study near 120°E China Based on Na LIDAR Observations" Remote Sensing 14, no. 19: 4798. https://doi.org/10.3390/rs14194798
APA StyleZou, X., Yang, G., Batista, P. P., Wang, J., Andrioli, V. F., Cheng, X., Jiao, J., Du, L., Zhang, T., Yang, H., Wang, Z., & Xia, Y. (2022). Gravity Wave Parameters and Their Seasonal Variations Study near 120°E China Based on Na LIDAR Observations. Remote Sensing, 14(19), 4798. https://doi.org/10.3390/rs14194798