Evaluation of Arctic Sea Ice Drift Products Based on FY-3, HY-2, AMSR2, and SSMIS Radiometer Data
Abstract
:1. Introduction
2. Data
2.1. Satellite Data
2.1.1. SSMIS Data
2.1.2. AMSR2 Data
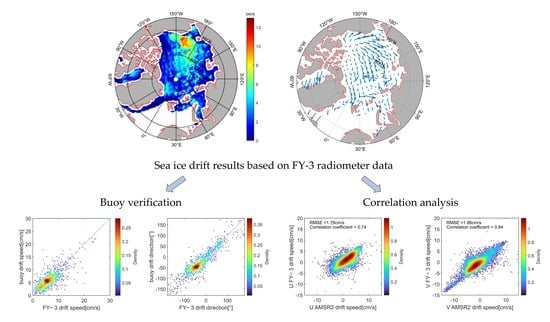
2.1.3. FY-3 Data
2.1.4. HY-2 Data
2.2. Auxiliary Data
2.3. Buoy Data
3. Methods
3.1. Gridding Brightness Temperature Data
3.2. Retrieval of Sea Ice Drift
3.2.1. Gauss Laplace Filter
3.2.2. Making a Mask
3.2.3. Continuous Maximum Cross-Correlation Matching
3.2.4. Quality Control
3.2.5. Polarization Fusion
3.3. Evaluation Indicators
4. Results
4.1. Accuracy of Satellite Products
4.1.1. Effect of Time Interval on the Accuracy of Sea Ice Drift Retrievals
4.1.2. Effect of Frequency on the Accuracy of Sea Ice Drift Retrievals
4.1.3. Drift Speed Error Distribution
4.2. Correlation between Retrieved Drift Speeds
5. Discussion
6. Conclusions
- High-accuracy ice drift products can be obtained from FY-3 and HY-2 radiometer bright temperature data. Comparing ice drift vectors retrieved from IABP buoy data and 37 GHz satellite data in a 6-day time interval, we found that the errors in the FY-3 (RMSEs in the drift speed and direction relative to buoy data: 0.77 cm/s and 6.49°; REs in the drift speed and direction relative to buoy data: 4.38% and 9.23%) and HY-2 (RMSEs in the drift speed and direction: 1.40 cm/s and 7.31°; REs in the drift speed and direction: 5.78% and 6.44%) products were slightly higher than those in the SSMIS (RMSEs in the drift speed and direction: 0.52 cm/s and 5.56°; REs in the drift speed and direction: 2.37% and 8.50%) and AMSR2 (RMSEs in the drift speed and direction: 0.51 cm/s and 5.36°; REs in the drift speed and direction: 2.42% and 8.32%) products. In general, the accuracies of the HY-2 and FY-3 products were slightly lower than those of the SSMIS and AMSR2 products, but the differences were small and met the international requirements for ice drift products.
- There is a close agreement between the sea ice drift vectors retrieved from the four sets of satellite data. Between the FY-3, SSMIS, and AMSR2 products, correlation coefficients and RMSEs were higher at 37 GHz (correlation coefficients: 0.76–0.86; RMSEs: 1.58–2.28 cm/s) than at 89 GHz (correlation coefficients: 0.58–0.84; RMSEs: 1.78–2.46 cm/s). In general, the correlation between FY-3, SSMIS, and AMSR2 products was high, while the correlation between HY-2 and the other products was low. Discrete point values in regions of low drift speeds impacted retrieval results.
- There was consistency between the spatial distributions of drift speeds retrieved from the four sets of radiometer data. Differences between products were negatively correlated with sea ice concentrations; large differences were associated with low sea ice concentrations. The retrieved sea ice drift speed was high in northern Alaska and extremely low in the northern Canadian Archipelago. There were spatial differences in the speed and direction of the different products; the largest differences were concentrated at the ice edge and between eastern Iceland and western Russia; this reflects the influence of the sea ice concentration on the spatial distribution of ice drift. Differences in the drift speeds were large in areas with low ice concentrations and small in areas with high ice concentrations. Retrievals of sea ice drift can be used in the formulation of local marine protection measures.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, M.; Yan, R.; Zhang, J.; Xu, Y.; Chen, P.; Shi, L.; Wang, J.; Zhong, S.; Zhang, X. Arctic Sea Ice Classification Based on CFOSAT SWIM Data at Multiple Small Incidence Angles. Remote Sens. 2022, 14, 91. [Google Scholar] [CrossRef]
- Liu, M.; Dai, Y.; Zhang, J.; Zhang, X.; Meng, J. Analysis of sea-ice condition in the Bohai Sea based on multi-source remote sensing data in the 2009–2010 winter. Dragon 3mid Term Results 2014, 724, 92. [Google Scholar]
- Zhang, F.; Pang, X.; Lei, R.; Zhai, M.; Zhao, X.; Cai, Q. Arctic sea ice motion change and response to atmospheric forcing between 1979 and 2019. Int. J. Climatol. 2022, 42, 1854–1876. [Google Scholar] [CrossRef]
- Spreen, G.; Kwok, R.; Menemenlis, D. Trends in Arctic sea ice drift and role of wind forcing: 1992–2009. Geophys. Res. Lett. 2011, 38, 19. [Google Scholar] [CrossRef] [Green Version]
- Ji, Q. Spatial and Temporal Variation of Arctic Sea Ice Thickness Based on Satellite Altimetry. Ph.D. Thesis, Wuhan University, Wuhan, China, 2015. [Google Scholar]
- Amstrup, S.C.; DeWeaver, E.T.; Douglas, D.; Marcot, B.G.; Durner, G.M.; Bitz, C.; Bailey, D.A. Greenhouse gas mitigation can reduce sea-ice loss and increase polar bear persistence. Nature 2010, 468, 955–958. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, H. Analysis of global sea ice simulation with BCC_CSM model and its error causes. In Proceedings of the 32nd Annual Meeting of Chinese Meteorological Society, Tianjin, China, 14 October 2015; p. 170. [Google Scholar]
- Qiu, B.; Li, C.; Guan, C. Effects of Arctic sea ice drift on multi-year ice distribution. Bull. Oceanol. Limnol. Sin. 2019, 3, 11. [Google Scholar]
- Denis, D.; Vladimir, V.; Eduard, K. Sea Ice Drift Tracking From Sequential SAR Images Using Accelerated-KAZE Features). IEEE Trans. Geosci. Remote Sens. 2017, 55, 5174–5184. [Google Scholar]
- Ye, Y.; Mohammed, S.; Georg, H.; Gunnar, S. Improving Multiyear Sea Ice Concentration Estimates with Sea Ice Drift. Remote Sens. 2016, 8, 397. [Google Scholar] [CrossRef] [Green Version]
- Ron, K. Sea ice concentration estimates from satellite passive microwave radiometry and openings from SAR ice motion. Geophys. Res. Lett. 2002, 29, 9. [Google Scholar]
- Jiménez, C.; Tenerelli, J.; Prigent, C.; Kilic, L.; Lavergne, T.; Skarpalezos, S.; Høyer, J.; Reul, N.; Donlon, C. Ocean and Sea Ice Retrievals From an End-To-End Simulation of the Copernicus Imaging Microwave Radiometer (CIMR) 1.4–36.5 GHz Measurements. J. Geophys. Res. Ocean. 2021, 126, 12. [Google Scholar] [CrossRef]
- Ming, Z.; Junkai, W.; Xiaoqi, L.; Xi, Z.; Jing, L.; Genwang, L.; Ting, Z. Detection of sea ice drift based on different polarization data. Laser Optoelectron. Prog. 2019, 56, 6. [Google Scholar]
- Zhang, M.; An, J.; Zhang, J.; Yu, D.; Wang, J.; Lv, X. Application of Feature Tracking and Pattern Matching Algorithm in Sea ice Drift Detection. Laser Optoelectron. Prog. 2019, 56, 7. [Google Scholar]
- Xu, J.; Zhang, X.; Wang, K. Sea ice drift monitoring method based on bilateral function global motion model. Spacecr. Eng. 2019, 28, 6. [Google Scholar]
- Hong, S.H.; Kim, J.H.; Park, J.W.; Won, J.S. Detection and Speed Measurement of Brash Ice in the Arctic Ocean by TerraSAR-X Quad-pol SAR. J. Coast. Res. 2019, 90, 1. [Google Scholar] [CrossRef]
- Wang, Y. Non-Homologous Sea ice SAR Image Registration Based on Significant Gray Difference; Dalian Maritime University: Dalian, China, 2020. [Google Scholar]
- Zhang, X.; Zhu, Y.; Zhang, J.; Meng, J.; Li, X.; Li, X. An Algorithm for Sea Ice Drift Retrieval Based on Trend of Ice Drift Constraints from Sentinel-1 SAR Data. J. Coast. Res. 2020, 102, 113–126. [Google Scholar] [CrossRef]
- Zhang, M.; An, J.; Zhang, J.; Yu, D.; Wang, J.; Lv, X. Enhanced Delaunay Triangulation Sea Ice Tracking Algorithm with Combining Feature Tracking and Pattern Matching. Remote Sens. 2020, 12, 581. [Google Scholar] [CrossRef] [Green Version]
- Dierking, W.; Stern, H.; Hutchings, J.K. Estimating statistical errors in retrievals of ice speed and deformation parameters from satellite images and buoy arrays. Cryosphere 2020, 14, 2999–3016. [Google Scholar] [CrossRef]
- Shokr, M.E.; Wang, Z.; Liu, T. Sea ice drift and arch evolution in the Robeson Channel using the daily coverage of Sentinel-1 SAR data for the 2016–2017 freezing season. Cryosphere 2020, 14, 3611–3627. [Google Scholar] [CrossRef]
- Barbat, M.M.; Rackow, T.; Wesche, C.; Hellmer, H.H.; Mata, M.M. Automated iceberg tracking with a machine learning approach applied to SAR imagery: A Weddell sea case study. ISPRS J. Photogramm. Remote Sens. 2021, 172, 189–206. [Google Scholar] [CrossRef]
- Xu, L.; Wong, W. A KPCA texture feature model for efficient segmentation of RADARSAT-2 SAR sea ice imagery. Int. J. Remote Sens. 2014, 35, 5053–5072. [Google Scholar] [CrossRef]
- Agnew, T.A.; Le, H.; Hirose, T. Estimation of large-scale sea-ice motion from SSM/I 85.5 GHz imagery. Ann. Glaciol. 1997, 25, 305–311. [Google Scholar] [CrossRef] [Green Version]
- Ninnis, R.M.; Emery, W.J.; Collins, M.J. Automated extraction of pack ice motion from advanced very high resolution radiometer imagery. J. Geophys. Res. Ocean. 1986, 91, 10725–10734. [Google Scholar] [CrossRef]
- Kwok, R.; Schweiger, A.; Rothrock, D.A.; Pang, S.; Kottmeier, C. Sea ice motion from satellite passive microwave imagery assessed with ERS SAR and buoy motions. J. Geophys. Res. Ocean. 1998, 103, 8191–8214. [Google Scholar] [CrossRef]
- Lavergne, T.; Eastwood, S.; Teffah, Z.; Schyberg, H.; Breivik, L.-A. Sea ice motion from low-resolution satellite sensors: An alternative method and its validation in the Arctic. J. Geophys. Res.Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Lavergne, T.; Piñol Solé, M.; Down, E.; Donlon, C. Towards a swath-to-swath sea-ice drift product for the Copernicus Imaging Microwave Radiometer mission. Cryosphere 2021, 15, 3681–3698. [Google Scholar] [CrossRef]
- Xian, Y.; Petrou, Z.I.; Tian, Y.; Meier, W.N. Super-Resolved Fine-Scale Sea Ice Motion Tracking. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5427–5439. [Google Scholar] [CrossRef]
- Rozman, P.; Hölemann, J.A.; Krumpen, T.; Gerdes, R.; Köberle, C.; Lavergne, T.; Girard-Ardhuin, F. Validating satellite derived and modelled sea-ice drift in the Laptev Sea with in situ measurements from the winter of 2007/2008. Polar Res. 2010, 30, 157–171. [Google Scholar] [CrossRef]
- Hwang, B. Inter-comparison of satellite sea ice motion with drifting buoy data. Int. J. Remote Sens. 2013, 34, 8741–8763. [Google Scholar] [CrossRef]
- Johansson, A.M.; Berg, A. Agreement and Complementarity of Sea Ice Drift Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 9, 369–380. [Google Scholar] [CrossRef]
- Sumata, H.; Lavergne, T.; Girard-Ardhuin, F.; Kimura, N.; Tschudi, M.A.; Kauker, F.; Gerdes, R. An intercomparison of Arctic ice drift products to deduce uncertainty estimates. J. Geophys. Res. C Ocean. JGR 2014, 119, 4887–4921. [Google Scholar] [CrossRef] [Green Version]
- Lei, R.; Hoppmann, M.; Cheng, B.; Zuo, G.; Gui, D.; Cai, Q.; Belter, H.J.; Yang, W. Seasonal changes in sea ice kinematics and deformation in the Pacific Sector of the Arctic Ocean in 2018/19. Cryosphere 2021, 15, 1321–1341. [Google Scholar] [CrossRef]
- Haller, M.; Brümmer, B.; Müller, G. Atmosphere–ice forcing in the transpolar drift stream: Results from the DAMOCLES ice-buoy campaigns 2007–2009. Cryosphere 2014, 8, 275–288. [Google Scholar] [CrossRef] [Green Version]
- Ito, K.; Xiong, K. Gaussian filter for nonlinear filtering problems. IEEE Conf. Decis. Control/IEEE 2002, 45, 910–927. [Google Scholar]
- Shi, L.; Drews, E.P.; Skinner, L. Static dielectric constant and infrared (below 1000 cm(−1)) spectrum for ice Ih: The effects of proton disorder and polarizability. Abstr. Pap. Am. Chem. Soc. 2013, 246, 1155. [Google Scholar]
- Meier, W.N.; Dai, M. High-resolution sea-ice motions from AMSR-E imagery. Ann. Glaciol. 2006, 44, 352–356. [Google Scholar] [CrossRef]















| Data Source | Coordinate System | Swath Width | Frequencies | Spatial Resolution | Polarization Mode |
|---|---|---|---|---|---|
| SSMIS | Hughes 1980 | 3000 km | 37 GHz/ 91 GHz | 25 km × 25 km/ 12.5 km × 12.5 km | H/V |
| AMSR2 | Hughes 1980 | 1450 km | 37 GHz/ 89 GHz | 25 km × 25 km/ 12.5 km × 12.5 km | H/V |
| FY-3 | WGS84 | 1400 km | 36.5 GHz/ 89 GHz | 18 km × 30 km/ 9 km × 15 km | H/V |
| HY-2 | WGS84 | 1600 km | 37 GHz | 20 km × 35 km | H/V |
| Data | HY-2 | FY-3 | SSMIS | AMSR2 | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | S (cm/s) | D (°) | S (cm/s) | D (°) | S (cm/s) | D (°) | S (cm/s) | D (°) |
| 3 d | 2.85 | 8.12 | 1.34 | 7.98 | 0.92 | 6.83 | 0.73 | 6.49 |
| 6 d | 1.40 | 7.31 | 0.77 | 6.49 | 0.52 | 5.56 | 0.51 | 5.36 |
| 14 d | 0.56 | 6.70 | 0.45 | 6.03 | 0.33 | 4.45 | 0.32 | 4.48 |
| Data | HY-2 | FY-3 | SSMIS | AMSR2 | ||||
|---|---|---|---|---|---|---|---|---|
| RE (%) | S | D | S | D | S | D | S | D |
| 3 d | 10.41 | 7.52 | 7.21 | 7.80 | 4.00 | 10.83 | 3.70 | 5.30 |
| 6 d | 5.78 | 6.44 | 4.38 | 9.23 | 2.37 | 8.50 | 2.42 | 8.32 |
| 14 d | 3.83 | 15.45 | 3.05 | 9.70 | 2.28 | 9.14 | 2.22 | 7.27 |
| Data | FY-3 | SSMIS | AMSR2 | |||
|---|---|---|---|---|---|---|
| RMSE | S (cm/s) | D (°) | S (cm/s) | D (°) | S (cm/s) | D (°) |
| 37 GHz (January to February) | 1.46 | 7.76 | 0.79 | 7.05 | 0.72 | 7.05 |
| 37 GHz (March to April) | 1.30 | 8.06 | 1.04 | 6.55 | 0.74 | 6.31 |
| 89 GHz (January to February) | 0.88 | 7.89 | 0.87 | 7.29 | 0.77 | 6.89 |
| 89 GHz (March to April) | 1.12 | 7.29 | 0.89 | 7.16 | 1.20 | 7.17 |
| Data | FY-3 | SSMIS | AMSR2 | |||
|---|---|---|---|---|---|---|
| RMSE | S (cm/s) | D (°) | S (cm/s) | D (°) | S (cm/s) | D (°) |
| 37 GHz (January to February) | 0.75 | 6.68 | 0.59 | 6.29 | 0.49 | 5.88 |
| 37 GHz (March to April) | 0.77 | 6.42 | 0.51 | 5.56 | 0.51 | 5.36 |
| 89 GHz (January to February) | 0.58 | 5.99 | 0.51 | 6.92 | 0.50 | 6.03 |
| 89 GHz (March to April) | 0.70 | 7.13 | 0.49 | 5.85 | 0.53 | 6.14 |
| Data | FY-3 | SSMIS | AMSR2 | |||
|---|---|---|---|---|---|---|
| RMSE | S (cm/s) | D (°) | S (cm/s) | D (°) | S (cm/s) | D (°) |
| 37 GHz (January to February) | 0.39 | 5.29 | 0.29 | 4.01 | 0.26 | 3.74 |
| 37 GHz (March to April) | 0.47 | 6.36 | 0.38 | 4.84 | 0.38 | 4.66 |
| 89 GHz (January to February) | 0.36 | 4.49 | 0.32 | 3.96 | 0.30 | 3.71 |
| 89 GHz (March to April) | 0.44 | 6.44 | 0.42 | 5.38 | 0.41 | 6.24 |
| Data | FY-3 | SSMIS | AMSR2 | |||
|---|---|---|---|---|---|---|
| RE (%) | S | D | S | D | S | D |
| 37 GHz (January to February) | 7.50 | 9.25 | 4.04 | 7.69 | 3.95 | 6.02 |
| 37 GHz (March to April) | 6.84 | 6.39 | 4.05 | 15.14 | 3.50 | 4.54 |
| 89 GHz (January to February) | 3.73 | 6.99 | 4.27 | 6.80 | 3.39 | 6.09 |
| 89 GHz (March to April) | 21.41 | 5.72 | 17.42 | 15.62 | 19.83 | 5.90 |
| Data | FY-3 | SSMIS | AMSR2 | |||
|---|---|---|---|---|---|---|
| RE (%) | S | D | S | D | S | D |
| 37 GHz (January to February) | 4.72 | 10.29 | 2.11 | 11.16 | 1.95 | 10.93 |
| 37 GHz (March to April) | 4.20 | 7.49 | 2.83 | 5.57 | 3.08 | 5.17 |
| 89 GHz (January to February) | 2.55 | 11.33 | 2.40 | 9.09 | 2.16 | 7.68 |
| 89 GHz (March to April) | 3.97 | 11.01 | 3.24 | 9.20 | 3.27 | 4.85 |
| Data | FY-3 | SSMIS | AMSR2 | |||
|---|---|---|---|---|---|---|
| RE (%) | S | D | S | D | S | D |
| 37 GHz (January to February) | 2.13 | 12.88 | 1.47 | 16.40 | 1.40 | 7.91 |
| 37 GHz (March to April) | 4.12 | 3.76 | 3.29 | 3.33 | 3.24 | 3.83 |
| 89 GHz (January to February) | 1.82 | 17.18 | 1.62 | 9.65 | 1.52 | 10.90 |
| 89 GHz (March to April) | 3.39 | 12.37 | 3.59 | 12.12 | 3.04 | 9.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Zhang, X.; Shi, L.; Bao, M.; Liu, G.; Cao, C.; Zhang, J. Evaluation of Arctic Sea Ice Drift Products Based on FY-3, HY-2, AMSR2, and SSMIS Radiometer Data. Remote Sens. 2022, 14, 5161. https://doi.org/10.3390/rs14205161
Fang H, Zhang X, Shi L, Bao M, Liu G, Cao C, Zhang J. Evaluation of Arctic Sea Ice Drift Products Based on FY-3, HY-2, AMSR2, and SSMIS Radiometer Data. Remote Sensing. 2022; 14(20):5161. https://doi.org/10.3390/rs14205161
Chicago/Turabian StyleFang, Hailan, Xi Zhang, Lijian Shi, Meng Bao, Genwang Liu, Chenghui Cao, and Jie Zhang. 2022. "Evaluation of Arctic Sea Ice Drift Products Based on FY-3, HY-2, AMSR2, and SSMIS Radiometer Data" Remote Sensing 14, no. 20: 5161. https://doi.org/10.3390/rs14205161
APA StyleFang, H., Zhang, X., Shi, L., Bao, M., Liu, G., Cao, C., & Zhang, J. (2022). Evaluation of Arctic Sea Ice Drift Products Based on FY-3, HY-2, AMSR2, and SSMIS Radiometer Data. Remote Sensing, 14(20), 5161. https://doi.org/10.3390/rs14205161