Energy-Based Adversarial Example Detection for SAR Images

Abstract

Adversarial examples (AEs) bring increasing concern on the security of deep-learning-based synthetic aperture radar (SAR) target recognition systems. SAR AEs with perturbation constrained to the vicinity of the target have been recently in the spotlight due to the physical realization prospects. However, current adversarial detection methods generally suffer severe performance degradation against SAR AEs with region-constrained perturbation. To solve this problem, we treated SAR AEs as low-probability samples incompatible with the clean dataset. With the help of energy-based models, we captured an inherent energy gap between SAR AEs and clean samples that is robust to the changes of the perturbation region. Inspired by this discovery, we propose an energy-based adversarial detector, which requires no modification to a pretrained model. To better distinguish the clean samples and AEs, energy regularization was adopted to fine-tune the pretrained model. Experiments demonstrated that the proposed method significantly boosts the detection performance against SAR AEs with region-constrained perturbation.

1. Introduction

Deep neural networks (DNNs) have achieved remarkable performance on synthetic aperture radar (SAR) target recognition [1]. However, adversarial attacks [2] have drawn wide public concern on the security of applicable DNN models. By adding imperceptible perturbation to a clean image, the so-called adversarial example (AE) can fool a pretrained DNN model into outputting any predictions specified by the attacker. Classic adversarial attacks [3,4,5,6] have become benchmarks to measure the robustness of neural networks. The latest research has proven that optical attacks maintain high performance when attacking DNN-based SAR image recognition models [7,8,9,10].

To meet the challenges posed by adversarial attacks, researchers have paid attention to adversarial defense. Current defenses can be decomposed to construct robust models and detect malicious inputs, i.e., adversarial detection. The first aims to improve the adversarial robustness of DNN models and correctly identify the real label of AEs [11,12,13]. The second only determines whether the test samples are AEs, such as the local intrinsic dimensionality detector (LID) [14] and Mahalanobis detector (MD) [15] in optics and the soft threshold detector (STD) [16] for remote sensing images. Adversarial detection endows DNN models with the ability to perceive the on-going adversarial attacks and has received more attention on SAR image recognition in adversarial situations.

Different from optical images, each pixel in a SAR image represents the scattering energy of electromagnetic waves reflected from the imaging area. For the physical realization, global perturbation AEs require changing the scattering characteristics of the entire imaging region, which is a rather costly task. A feasible idea is to restrict the perturbation to a certain region, and the corresponding research has recently been carried out. The current discussion focuses on generating adversarial perturbations near the target [17] and correlating the adversarial perturbation with electromagnetic signals [18] to reduce the physical realization difficulty of SAR AEs. Although no mature physical AE implementation method has been proposed yet, it is necessary to explore the security threat of region-constrained SAR AEs. From a defensive standpoint, we found that current detection methods expose performance degradation against SAR AEs with regional constraints. Designing defense methods robust to region-constrained adversarial perturbation is an ongoing challenge.

In this paper, we considered AEs to be low-probability samples that are incompatible with the clean dataset. Through energy-based models [19,20,21], we converted the probability criterion to an energy criterion, where a sample with higher energy corresponds to a stronger adversarial degree. Further, we found that there is an inherent energy gap between the distributions of clean samples and AEs on a pre-trained model, even when regional constraints are imposed on AEs. Based on this discovery, we propose the energy-based detector (ED) and the fine-tuned energy-based detector (FED) to solve the problem of detecting region-constrained SAR AEs. The contribution of this paper can be summarized as follows:

• We designed a novel energy feature space for SAR adversarial detection, where the adversarial degree of a sample is positively related to its energy.
• We propose an energy-based detector (ED), which requires no modification to the pretrained model. Compared with another unmodified detector, STD, the proposed method showed superior performance.
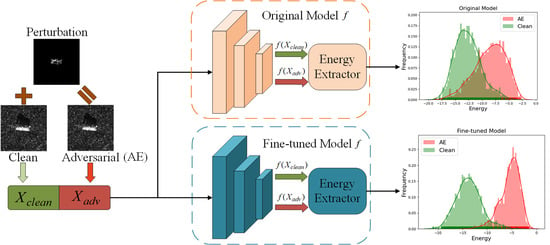
• On the basis of ED, we propose to fine-tune the pre-trained model with a hinge energy loss item to further optimize the output energy surface. Compared with the LID and MD, the proposed fine-tuned energy-based detector (FED) was experimentally demonstrated to boost the detection performance against SAR AEs, especially for those with regional constraints.

The rest of this paper is organized as follows. In Section 2, we briefly introduce the adversarial attack and adversarial detection methods used in this paper. In Section 2.3, we explore generating SAR AEs with region-constrained perturbation and analyze the weakness of current adversarial detection methods. In Section 3, we propose our energy-based detector (ED) and fine-tuned energy-based detector (FED). In Section 4, we provide the details of the experiment. Finally, the discussion and conclusion are summarized in Section 5.

2. Preliminaries

2.1. Adversarial Attack

Adversarial attacks can be divided into targeted attacks and untargeted attacks. The prediction of a targeted AE in the model is specified by the attacker, while the prediction of an untargeted AE is any category other than its true label. In practical applications, defenders cannot know which category the upcoming attack will target. When evaluating the performance of adversarial detection, generating untargeted AEs is a common process to ensure that the defense covers each category. Since this paper is on the defensive side, we introduced adversarial attacks in an untargeted manner.

Given a sample x with a ground truth label y, an discriminative model f estimates the category of x by calculating the conditional probability of the sample x on the category y:

$$p\left(y\right|x)=\frac{e^{f_y\left(x\right)}}{{\displaystyle \sum _i}{e}^{f_i\left(x\right)}}$$

(1)

where $f_i\left(x\right)$ represents the i-th component of the model’s output $f\left(x\right)$. The essence of adversarial attack is to increase a model’s cross-entropy loss by adding an l-norm constrained perturbation $\eta$ on a clean image x:

$$\begin{array}{cc}\hfill & \underset{\eta }{max}-\sum _{i}q\left(i\right)·logp\left(i\right|x+\eta )\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{∥\eta ∥}_l<\epsilon \hfill \end{array}$$

(2)

where $q\left(i\right)$ represents the ground truth probability of label i and $p\left(i\right|x+\eta )$ represents the conditional probability of $x+\eta$ on label i. For one-hot-encoded labels, Equation (2) can be simplified to:

$$\begin{array}{cc}\hfill & \underset{\eta }{max}-logp\left(y\right|x+\eta )\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{∥\eta ∥}_l<\epsilon \hfill \end{array}$$

(3)

That is, the AE fools DNN classifiers by reducing the conditional probability of sample $x+\eta$ on the ground truth label y.

The core of the adversarial attack is to design a suitable perturbation function $\eta (·)$:

• FGSM: The fast gradient sign method (FGSM) [3] normalizes the gradients of the input with respect to the loss of model f to the smallest pixel depth as a perturbation unit:

  $${\eta }_{FGSM}\left(x\right)=sign\left({\nabla }_{x}Loss(f\left(x\right),y)\right)$$

  (4)
• BIM: The basic iterative method (BIM) [4] optimizes the FGSM attack as an iterative version:

  $${\eta }_{BIM}\left(x_{i+1}\right)=sign\left({\nabla }_{x_i}Loss(f\left(x_i\right),y)\right)$$

  (5)
• DeepFool: Moosavi-Dezfooli et al. [5] added iterative perturbations until the AE crosses a linearly assumed decision boundary, and the perturbation in each iteration is calculated as

  $${\eta }_{DeepFool}\left(x_{i+1}\right)=\underset{k}{min}\frac{f_y\left(x_i\right)-f_k\left(x_i\right)}{{\nabla }_y{f}_y\left(x_i\right)-{\nabla }_{k}f\left(x_i\right)}$$

  (6)
• CW: To avoid clamping AEs between $(0,1)$ in every iteration, Carlini and Wagner [6] introduced a new variable w to express the AE as $\frac{1}{2}(tanh\left(w\right)+1)$, which maps the value of the AE smoothly lying between $(0,1)$. The perturbation is expressed as:

  $${\eta }_{CW}\left(x\right)=\frac{1}{2}(tanh\left(w\right)+1)-x$$

  (7)

2.2. Adversarial Detection

Adversarial detection is essentially a binary classification problem where clean samples are treated as positives and AEs are negatives. Given a test sample x, the detector D judges its adversarial property according to a well-designed metric function M and a threshold $\alpha$:

$$D\left(x\right)=\left\{\begin{array}{c}\mathrm{adversarial},\\ \mathrm{clean},\end{array}\right.\begin{array}{c}M\left(x\right)\ge \alpha ,\\ M\left(x\right)<\alpha .\end{array}$$

(8)

The core of adversarial detection is to find a suitable metric function M:

• Local intrinsic dimensionality detector (LID): Ma et al. [14] supposed that the AEs lie in the high-dimensional region of the feature manifold and, therefore, own higher local intrinsic dimensionality (LID) values compared with clean samples. Given a test sample x, the LID method randomly picks k samples in the training set and calculates the LID value of sample x as follows:

  $$M_{LID}\left(x\right)=-{(\frac{1}{k}\sum _{i=1}^{k}log\frac{r_i\left(x\right)}{r_k\left(x\right)})}^{-1}$$

  (9)

  where $r_i\left(x\right)$ represents the featurewise Euclidean distance from sample x to its i-th nearest neighbor.
• Mahalanobis detector (MD): Lee et al. [15] adopted the featurewise Mahalanobis distance to measure the adversarial degree of a test sample x under the assumption that clean samples obey the class conditional Gaussian distribution in the feature space, while the AEs do not. With the feature vector before the classification layer of sample x defined as $V\left(x\right)$, the metric function of the MD method is calculated as

  $$M_{MD}\left(x\right)=\left(V\left(x\right)-{\mu }_k\right){\sum }^{-1}{\left(V\left(x\right)-{\mu }_k\right)}^T$$

  (10)

  where ${\mu }_k$ is the mean feature vector of the predicted label k of x on the training set and ∑ is the feature covariance matrix.
• Soft threshold detector (STD): Li et al. [16] found that there are differences in classification confidence between clean samples and AEs, and a lower confidence corresponds to a higher adversarial degree. Based on this finding, the authors recreated a new dataset consisting only of classification confidence and binarized labels and trained a logistic regression classifier to obtain the best confidence threshold $\alpha$ for each class. The metric function M of the STD method can be expressed as

  $$M_{STD}=-p(argmaxf\left(x\right)|x)$$

  (11)

The LID [14] and MD [15] require disassemble the model to extract the intermediate layer features, so they are usually considered as modified methods, while the STD [16] only checks the output of the model, which is an efficient unmodified method.

2.3. Problem of Detecting SAR AEs under Regional Constraint

The regional constraint of the perturbation has attracted wide attention when generating SAR AEs. Different from the physical implementation method of optical AEs, such as directly pasting adversarial patches [22,23,24], SAR images reflect the energy distribution of the scattered points formed by the electromagnetic echo of the target after being processed by the Fourier transform. Although there is yet no physical implementation method for SAR AEs, a feasible idea is to constrain the adversarial attack to a specific region to reduce the difficulty of coupling the perturbation with signals. How to defend against SAR AEs with the region constraint is a practical problem that needs to be studied urgently. In this paper, we explored the influence of four different regional constraint functions, as shown in Figure 1. Under the regional constraint, the objective function of the adversarial attack in Equation (3) will be different:

$$\begin{array}{cc}\hfill & \underset{\eta }{max}-logp\left(y\right|x+R\odot \eta )\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{∥R\odot \eta ∥}_p<\epsilon \hfill \end{array}$$

(12)

where the constraint term R can be understood as a mask with the specified pixels of 1 and others of 0 and works by taking the Hadamard product ⊙ with the original perturbation $\eta$. The open SAR dataset MSTAR [25] and its publicly accessible segmentation annotation SARbake [26] were used as an auxiliary to design the region constraint mask R.

Taking the FGSM AE as an example, we discuss the impact of regional constraints on three classical adversarial detection methods [14,15,16], as shown in Figure 2:

• Impact on the LID and MD: The LID and MD implement detection by examining the intermediate features of the test samples. However, as the regional constraint became tightened, the detection performance of the LID and MD showed a significant drop, with the AUROC dropping by nearly 20% in the worst case. This reveals that SAR AEs under the regional constraint not only expose smaller visual observability, but also have less difference in intermediate features from clean samples.
• Impact on the STD: The STD method detects AEs by checking the output confidence. It can be seen that the regional constraint had relatively less impact on the output layer of the model. However, since the STD method is still based on the conditional confidence $p\left(y\right|x)$, it did not perform as well as the LID and MD, despite its computational efficiency.

3. Proposed Method

As discussed in Section 2.3, the regional constraints bring severe performance degradation to the detection methods based on intermediate features [14,15]. Although the output confidence-based method [16] is less affected by the regional constraint, it yet has limited performance due to checking the conditional probability $p\left(y\right|x)$. We hope to find a method combining both high performance and robustness to regional constraints. Different from the conditional probabilities $p\left(y\right|x)$ at the output level, we believe that $p\left(x\right)$ is a more reasonable choice to measure the adversarial degree of a test sample.

3.1. Interpretability of $p\left(x\right)$

As shown in Equation (3), the essence of an adversarial attack is to reduce the conditional probability $p\left(y\right|x)$ (confidence) of a clean sample as the true class, so that the model misjudges the corresponding AE as the wrong class. However, researchers [3,6] have shown that AEs also have high confidence (nearly 100%) in the wrong category, which results in the inability of conditional-probability-based criteria to distinguish high-confidence AEs.

Given a training set consisting of clean samples $\varsigma =\left\{(x,y)|x\in {\mathbb{R}}^{w\times h},y\in \mathbb{R}\right\}$, the marginal distribution $p\left(x\right)$ is usually thought of as the probability of x being sampled in the training set $\varsigma$. By decomposing $p\left(x\right)$ into the sum of joint distributions $p(x,i)$ on a k-classification model, we provide a new perspective on $p\left(x\right)$:

$$p\left(x\right)=\sum _i^{K}p(x,i)$$

(13)

The joint distribution $p(x,i)$ measures the probability that sample x and label i occur at the same time or how much sample x is compatible with label i. Then, $p\left(x\right)$ can be interpreted as the compatibility of x with the entire training set $\varsigma$. It is well known that AEs and clean samples are visually similar $x_{adv}\approx x$, but their predicted labels in a DNN model are quite different $y_{adv}\ne y$. Hence, our core idea is that AEs are incompatible with the clean training set $\varsigma$, indicating a low $p\left(x\right)$.

3.2. Energy-Based Detector on Pretrained Model

It is intractable to calculate $p\left(x\right)$ through the sum of the joint distribution by Equation (13) on a discriminative model. Energy-based models [19,20,21] offer a new approach to this problem. LeCun et al. [19] pointed out that any probability density $p\left(x\right)$ for $x\in \mathbb{R}$ can be expressed in the form of an free energy function:

$$p\left(x\right)=\frac{e^{-E\left(x\right)}}{\underset{x}{\int }{e}^{-E\left(x\right)}dx}=\frac{e^{-E\left(x\right)}}{Z},$$

(14)

where $E\left(·\right)$ is the free energy function, which maps a sample x to a scalar value. The constant $Z=\underset{x}{\int }{e}^{-E\left(x\right)}dx$ is known as the partition function, which normalizes the probability between 0 and 1. After taking the logarithm of both sides of Equation (14), we can find that $logp\left(x\right)$ is linearly aligned with $E\left(x\right)$:

$$logp\left(x\right)=-E\left(x\right)-logZ$$

(15)

where a larger $p\left(x\right)$ corresponds to a smaller $E\left(x\right)$. Hence, the problem of solving $p\left(x\right)$ can be transformed into solving $E\left(x\right)$. Will et al. [20] revealed that one can reinterpret a standard discriminative classifier of $p\left(y\right|x)$ as an energy-based model for the joint distribution $p(x,y)$:

$$p(x,y)=\frac{e^{f_y\left(x\right)}}{Z}$$

(16)

where $f_y$ is the y-th component of the model’s output $f\left(x\right)$ and Z is the constant partition function. According to the Bayes rule and Equation (1):

$$p(x,y)=p\left(x\right)·p\left(y\right|x)=\frac{e^{-E\left(x\right)}}{Z}·\frac{e^{f_y\left(x\right)}}{{\displaystyle \sum _{i=0}^K}{e}^{f_i\left(x\right)}}$$

(17)

where K is the total number of categories. By connecting Equations (16) and (17), we obtain the explicit expression for $E\left(x\right)$:

$$E\left(x\right)=-log\sum _{i=0}^K{e}^{f_i\left(x\right)}$$

(18)

where the energy $E\left(x\right)$ is defined by the model’s output $f\left(x\right)$. For clean samples, the logarithm of its probability $p\left(x\right)$ is larger, corresponding to lower energy $E\left(x\right)$, while AEs have a smaller $p\left(x\right)$, corresponding to a higher $E\left(x\right)$.

To confirm our assumption, we visualize the energy distribution of clean samples and AEs on the test set, as shown in Figure 3. It can be observed that there is an “energy gap” between the energy distributions of clean samples and AEs even when the regional constraint is imposed on AEs. The high-energy AEs and low-energy clean samples naturally belong to two different distributions. By setting an appropriate decision threshold $\alpha$, it is feasible to achieve the distinction between AEs and clean samples. Hence, we trained a logistic regression model on a small validation set ${\varsigma }_{val}$, where clean samples and the corresponding AEs are labeled as positives and negatives, respectively. Then, the energy value corresponding to a 95% true positive rate is set as the threshold $\alpha$. We provide the pseudocode for training our energy detector (ED) in Algorithm 1.

Algorithm 1: Energy-based adversarial detector (ED).

3.3. Energy-Based Detector on Fine-Tuned Model

Although there is an inherent energy difference between AEs and clean samples on a pretrained model, we hope to increase this “energy gap”. Hence, we define a new objective function to fine-tune a pretrained model:

$$\underset{\theta }{min}{\mathrm{L}}_{CE}+\lambda L_{EG}$$

(19)

The former item ${\mathrm{L}}_{CE}$ is the simplified cross-entropy loss derived from Equations (2) and (3), which keeps the classification accuracy of the model for clean samples:

$$L_{CE}=-logp\left(y\right|x)$$

(20)

The latter item $L_{EG}$ is the energy loss, which enlarges the energy gap between the clean samples and AEs, and $\lambda$ is the regularization coefficient. We used the hinge function to define the energy loss:

$$L_{EG}=max(0,E\left(x_{clean}\right)-E_{LB})+max(0,E_{UB}-E\left(x_{adv}\right))$$

(21)

where $E_{LB}$ and $E_{UB}$ are the lower bound and upper bound of energy, respectively. This loss function is designed to penalize clean samples with an energy higher than the lower bound and AEs with an energy lower than the upper bound, so that an optimized energy surface can be obtained. The mean energy of clean samples and their corresponding AEs is calculated, respectively, in the validation set ${\varsigma }_{val}$ as the lower bound $E_{LB}$ and upper bound $E_{UB}$:

$$\begin{array}{cc}\hfill & E_{LB}=\frac{1}{N}\sum _{i=0}^{N}E\left(x_{clean}\right)\hfill \\ \hfill & E_{UB}=\frac{1}{N}\sum _{i=0}^{N}E\left(x_{adv}\right)\hfill \\ \hfill & x\in {\varsigma }_{val}\hfill \\ \hfill \end{array}$$

(22)

We verified the effectiveness of the proposed fine-tuning method on the same test set in Section 3.2. The flowchart of the FED detector and visualization of energy distributions are shown in Figure 4. It can be observed that, after fine-tuning by Equation (19), the energy gap between AEs and clean samples are significantly enlarged. The details of acquiring our fine-tuned energy detector are provided in Algorithm 2.

Algorithm 2: Fine-tuned energy-based detector (FED).

4. Results

In order to facilitate the reader’s understanding, we first introduce the overall experimental context. In Section 4.1, we describe the dataset details. In Section 4.3, we illustrate the training details of the original models and the parameters of the AEs. In Section 4.3, we introduce the evaluation metrics used in this paper. In Section 4.4, we explore the robustness of current attack methods towards regional constraints under a similar perturbation scale. In Section 4.5, we verify the detection performance of the proposed ED and FED methods against four classic AEs with three different regional constraints on three networks. In Section 4.6, we analyze the sensitivity of the parameter $\lambda$ and the convergence of the objective function Equation (19). In Section 4.7, we visualize the criteria distributions of different detection methods. In Section 4.8, we explore the detection performance of the proposed method against AEs with variable perturbation scales. In Section 4.9, we explore the robustness of the proposed method against adaptive attacks.

4.1. Dataset

We conducted our experiment on the most commonly used SAR dataset, the Moving and Stationary Target Acquisition and Recognition (MSTAR) dataset [25], which was funded by the Defense Advanced Research Projects Agency (DARPA) and the Air Force Research Laboratory (AFRL). MSTAR contains ten types of military targets at different azimuth and elevation angles, and each image is formed with one-channel amplitude information and a size of 128 × 128. In the original dataset, images with a depression angle of 17${}^{\circ }$ are used for training and images with depression angle of 15${}^{\circ }$ are used for testing. The optical and corresponding SAR images are shown in Figure 5.

4.2. Experiment Setups

We trained ResNet34 [27], VGG16 [28], and DenseNet121 [29] as the original models with the Adam optimizer. For FGSM and BIM, the perturbation scale was set as ${∥\eta ∥}_{\infty }=8/255$ and ${∥\eta ∥}_{\infty }=4\times 2/255$, respectively. For DeepFool and CW, we used the $L_2$-norm attack with the maximum number of iterations set as 30. The learning rate of w in CW and the overshoot in DeepFool were 0.01. We used the LID [14], MD [15], and STD [16] to detect the successful AEs whose predictions on the models were inconsistent with their true labels. Similar to the LID and MD, we added Gaussian noisy samples with the same perturbation scale as AEs to the test set to approximate the real application scenario. One-fifth of the test set was divided as the validation set. We used the Adam optimizer with a learning rate of ${10}^{-6}$ to fine-tune the energy surface of the pretrained model for 30 epochs. The energy regularization term $\lambda$ was set as 0.1.

4.3. Evaluation Metric

• ASR: We used the attack success rate (ASR) to measure the attack performance of the methods [2,4,5,6]:

  $$ASR=\frac{n_{success}}{n_{totol}}\times 100\%$$

  (23)

  where $n_{totol}$ and $n_{success}$ represent the number of generated AEs and the number of successful AEs, respectively.
• AUROC: The AUROC measures the area under the receiver operating characteristic curve, which takes a value between 0.5 and 1. The AUROC reflects the maximum potential of the detection methods.
• TNR@95%TPR: Since normal samples are in the majority and AEs are in the minority in practical applications, the detection rate against AEs (TNR) should be improved under the premise of maintaining the detection rate of normal samples (TPR), as shown in

  Table 1. Illustration of evaluation metric for detection.

  Adversarial: 0		Ground Truth
  Clean & Noisy: 1		1	0
  Prediction	1	True Positive (TP)	False Positive (FP)
  	0	False Negative (FN)	True Negative (TN)
  Indicator		$\mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}\times 100\%$	$\mathrm{TNR}=\frac{\mathrm{TN}}{\mathrm{FP}+\mathrm{TN}}\times 100\%$

  . Hence, we chose the true negative rate (TNR) at a 95 % true positive rate (TPR) to measure the performance of the detection methods.

4.4. Influence of Regional Constraint on Attack Performance

Firstly, we investigated the influence of the regional constraint on the attack performance. As shown in

Table 2. Influence of regional constraint on attack performance (ASR(%)).

Constraint		Global	R1	R2	R3
ResNet34	FGSM	96.0	65.9	28.2	3.0
	BIM	97.3	83.6	39.1	3.4
	CW	100	100	97.0	51.9
	DeepFool	98.9	73.1	56.29	9.6
DenseNet121	FGSM	93.1	97.2	70.0	20.6
	BIM	100	100	95.3	30.8
	CW	99.9	99.9	99.8	87.7
	DeepFool	99.9	95.9	55.4	4.4
VGG16	FGSM	97.8	71.4	35.2	4.8
	BIM	99.1	84.0	46.6	5.9
	CW	100	100	96.6	31.6
	DeepFool	96.3	64.7	33.1	0.7

Note: AEs with an ASR less than 10% are bolded.

, among four classic attacks, the regional constraint of the adversarial perturbation led to a general decrease of the ASR for SAR AEs, especially for the DeepFool [5] attack. This phenomenon may be related to the weakening of the perturbation strength that the regional constraint brings. The decreasing perturbation area caused less gradient rise and ultimately resulted in the decreasing of the ASR. Still, it is worth noting that the CW [6] attack maintained a considerable ASR even for R3 with a high constraint level, which shows promising prospects for designing practical SAR AEs.

4.5. Detection Performance

In this section, we evaluated the detection performance of the proposed method (ED and FED) against SAR AEs with the regional constraint. The proposed ED method requires no change to the original model, which is an unmodified method like the STD [16], while our FED method fine-tunes the parameters of the original model, which is a modified method like the LID [14] and MD [15]. To rule out the randomness, we did not detect AEs with an ASR less than 10%, because there was too little image to fine-tune the model.

As shown in

Table 3. Comparison of the AUROC against SAR AEs between the proposed methods and classic methods (%).

Attack Setup			Unmodified		Modified
Network	Attack	Region	STD	ED	LID	MD	FED
DenseNet121	FGSM	Global	73.2	74.6	98.3	99.5	99.6
		R1	69.7	70.2	91.1	88.8	98.8
		R2	76.4	78.3	79.7	74.3	96.8
		R3	89.6	91.9	64.3	53.1	96.7
	BIM	Global	89.6	73.0	99.3	99.4	98.9
		R1	93.1	82.5	99.8	99.2	97.3
		R2	55.7	64.7	96.8	94.9	98.2
		R3	52.6	72.3	82.2	88.3	89.6
	CW	Global	74.7	63.8	99.9	99.9	99.9
		R1	62.3	70.4	98.4	99.2	99.5
		R2	66.5	80.6	95.9	97.9	98.6
		R3	69.0	81.6	89.1	90.9	98.2
	DeepFool	Global	95.2	97.5	78.1	91.3	97.7
		R1	94.5	96.6	62.8	67.6	99.7
		R2	92.7	95.4	76.8	97.5	98.5
		R3	/	/	/	/	/
ResNet34	FGSM	Global	60.5	82.7	94.5	95.5	97.5
		R1	65.5	86.8	91.5	89.7	97.5
		R2	67.3	87.2	81.3	87.8	95.8
		R3	/	/	/	/	/
	BIM	Global	60.2	60.8	96.2	93.8	95.3
		R1	82.2	62.9	98.3	81.7	93.8
		R2	66.0	87.5	84.1	87.3	96.6
		R3	/	/	/	/	/
	CW	Global	66.3	62.1	98.0	95.9	96.8
		R1	60.5	78.4	96.3	88.7	97.8
		R2	65.5	87.1	93.4	91.8	98.3
		R3	68.4	87.8	86.6	90.6	98.1
	DeepFool	Global	60.0	97.6	81.8	98.2	98.8
		R1	65.4	98.3	78.1	98.5	98.8
		R2	62.2	98.2	74.2	98.5	98.7
		R3	/	/	/	/	/
VGG16	FGSM	Global	58.1	59.2	83.7	91.5	96.7
		R1	63.6	65.9	92.1	79.4	95.2
		R2	64.2	63.5	78.6	70.7	89.9
		R3	/	/	/	/	/
	BIM	Global	56.5	57.6	89.8	74.0	95.3
		R1	60.2	55.8	94.2	77.4	95.0
		R2	65.5	62.6	84.7	72.9	93.6
		R3	/	/	/	/	/
	CW	Global	65.2	78.9	99.7	99.5	99.9
		R1	60.0	61.9	97.4	84.1	97.0
		R2	70.9	71.5	92.8	87.3	97.3
		R3	68.3	71.7	80.0	76.1	90.9
	DeepFool	Global	86.8	88.4	53.9	63.8	97.3
		R1	71.1	86.0	69.4	75.6	96.4
		R2	76.4	82.2	67.5	75.0	93.4
		R3	/	/	/	/	/

Note: The best results are bolded.

and

Table 4. Comparison of the TNR@95%TPR against SAR AEs between the proposed methods and classic methods (%).

Attack Setup			Unmodified		Modified
Network	Attack	Region	STD	ED	LID	MD	FED
DenseNet121	FGSM	Global	37.4	45.7	95.7	99.6	98.9
		R1	23.0	37.9	53.0	31.5	94.6
		R2	26.2	42.9	16.4	3.2	85.4
		R3	39.1	61.8	4.1	0.35	80.6
	BIM	Global	74.2	46.1	98.1	98.4	96.4
		R1	84.1	63.3	99.6	97.2	91.7
		R2	29.3	16.1	86.4	77.6	93.5
		R3	8.1	15.3	37.8	33.6	56.3
	CW	Global	61.1	48.4	99.5	99.6	99.6
		R1	18.7	30.5	92.3	98.6	98.8
		R2	34.1	51.3	79.8	90.4	94.2
		R3	33.5	48.4	66.8	77.2	91.7
	DeepFool	Global	69.1	85.8	36.1	19.2	88.7
		R1	57.2	77.8	5.2	0.2	99.7
		R2	50.3	63.0	26.2	91.6	96.9
		R3	/	/	/	/	/
ResNet34	FGSM	Global	30.0	50.3	89.1	85.5	89.3
		R1	24.1	48.0	80.6	80.7	88.4
		R2	19.6	44.6	61.8	51.9	78.5
		R3	/	/	/	/	/
	BIM	Global	44.8	22.3	83.8	63.0	76.5
		R1	65.8	25.0	93.0	44.6	73.4
		R2	11.9	35.2	42.5	39.0	79.4
		R3	/	/	/	/	/
	CW	Global	40.7	18.9	90.2	72.7	85.9
		R1	14.0	32.5	80.4	64.6	90.9
		R2	11.5	51.6	69.8	72.4	92.8
		R3	16.3	43.6	51.8	51.2	90.5
	DeepFool	Global	62.5	96.3	59.8	94.7	98.9
		R1	65.4	95.4	49.7	94.9	98.6
		R2	62.2	95.0	46.3	96.3	97.3
		R3	/	/	/	/	/
VGG16	FGSM	Global	12.6	25.4	53.4	73.1	86.1
		R1	18.7	22.0	66.7	27.6	78.4
		R2	19.4	15.2	34.9	17.0	55.8
		R3	/	/	/	/	/
	BIM	Global	12.1	13.7	62.2	42.2	76.5
		R1	9.7	6.7	77.0	26.8	72.4
		R2	10.0	11.1	41.8	17.6	67.0
		R3	/	/	/	/	/
	CW	Global	10.3	49.5	99.8	100	100
		R1	9.9	19.8	85.9	49.3	86.6
		R2	10.7	14.4	68.6	57.2	88.1
		R3	12.0	19.1	44.6	17.0	53.4
	DeepFool	Global	37.9	41.8	40.4	45.3	85.5
		R1	25.1	29.7	21.4	24.8	82.4
		R2	21.3	25.7	20.0	22.3	63.1
		R3	/	/	/	/	/

Note: The best results are bolded.

, the proposed energy-based detector (ED) and fine-tuned energy-based detector (FED) achieved the highest score on the TNR@95%TPR and the AUROC among four classic adversarial attacks with four regional constraints on three models in most cases.

For unmodified detection, the proposed ED exhibited stronger performance than the STD [16], bringing average improvements by 10% on the TNR and AUROC. Different from the STD, which checks the conditional probability $p\left(y\right|x)$, our energy detector (ED) checks the energy $E\left(x\right)$ of a test sample, which is linearly aligned with $logp\left(x\right)$ and is more robust to adversarial attacks.

For modified detection, the proposed FED outperformed the LID [14] and MD [15] in most cases, especially for AEs with strong regional constraints, such as $R_2$ and $R_3$. Our FED method significantly boosted the detection performance against SAR AEs with region-constrained perturbation and achieved comparable performance against SAR AEs with global perturbation. The superiority of the proposed method was attributed to the inherent energy gap between AEs and natural samples.

Among four classic attacks, the proposed ED and FED had stable performance on FGSM [2], CW [6], and DeepFool [5] for both modified and unmodified detections. However, for the iterative BIM [4] attack, the ED and FED only performed effective detection against AEs with strong regional constraints (e.g., $R_2$ and $R_3$). This may be due to the reason that the BIM attack updates the perturbation direction iteratively and the corresponding AEs are more in line with the training set distribution.

As shown in

Table 5. Structure details of DenseNet121, ResNet34, and VGG16.

Network	DenseNet121	ResNet34	VGG16
Parameter	6.96M	21.29M	134.3M
Layer	121	34	16

, among the three DNN networks, all methods showed good applicability on DenseNet121 [29], while their performance was generally weaker on VGG16 [28]. Since DenseNet121 owns the deepest network layers and least network parameters, while VGG16 is exactly the opposite, we conjectured that the detection performance was positively correlated with the number of network layers and negatively correlated with the amount of network parameters.

4.6. Sensitivity Analysis

Parameter $\lambda$ characterizes the weight of regular term $L_{EG}$ in Equation (19). We explored the influence of parameter $\lambda$ on the detection performance against FGSM AEs and the classification accuracy for clean samples. Parameter $\lambda$ takes a value from 0 to 1, and the step size is 0.02 in $(0,0.2)$ and 0.05 in $(0.2,1)$. As shown in Figure 6a, as $\lambda$ increased, the TNR at a 95% TPR became stable on DenseNet121 and obtained a gradually decreasing range of fluctuation on ResNet34. For VGG16, the TNR experienced a decline in interval $(0.1,0.12)$ before convergence, which may be due to randomness in the generalization process. As shown in Figure 6b, the classification accuracy of all three models remained stable for different $\lambda$, which benefited from the cross-entropy term in Equation (19).

Objective function Equation (19) aims to enlarge the energy gap between AEs and clean samples while ensuring the accuracy on clean samples. As shown in Figure 6c, the fine-tuned loss on all three networks achieved convergence after 30 epochs, demonstrating the validity of the proposed fine-tuned method.

4.7. Visualization of Energy Distribution

In order to better verify the effectiveness of the ED and energy FED, we extracted the energy distribution of clean samples and the corresponding AEs with regional constraints on DenseNet121 [29], as shown in Figure 7. The AEs were generated on the test set by the FGSM method, and the energy of every sample was recorded in the form of a density distribution map. It can be observed that there was an inherent energy gap lying between clean samples and AEs; that was because the AEs did not belong to the natural training set and corresponded to a low probability (high energy). Furthermore, as the regional constraints became tightened, the distribution of the Mahalanobis distance and local intrinsic dimensionality of the AEs and clean samples became confused, while the energy distribution was more robust to the changes of the perturbation region.

4.8. Detection against AEs with Variable Perturbation Scales

In Section 4.4, the ASR of globally perturbed AEs was close to 100%, while there were only a few AEs having ASRs that exceeded the 10% detection threshold under the R3 constraint. Therefore, we studied the effect of reducing the global perturbation scale and increasing the R3 constraint perturbation scale. Specifically, for the convenience of controlling the perturbation scale, FGSM AEs were generated for testing. We reduced the global perturbation scale to 1/2 and 1/4 of the original scale, while under the R3 constraint, we doubled and quadrupled the original scale, respectively. We calculated the ASR of these AEs with variable perturbation scales, shown in

Table 6. ASR of AEs with variable perturbation scale (%).

	Attack	Global ($\mathit{ϵ}/4$)	Global ($\mathit{ϵ}/2$)	R3 ($\mathit{ϵ}\times 2$)	R3 ($\mathit{ϵ}\times 4$)
Network	DenseNet121	39.2	87.4	49.3	69.4
	ResNet34	12.6	43.6	28.1	60.9
	VGG16	68.5	92.4	55.9	68.4

and measured the detection performance, shown in

Table 7. Comparison of performance against AEs with various perturbation scales (AUROC%).

Attack Setup		Unmodified		Modified
Network	Region	STD	ED	LID	MD	FED
DenseNet121	Global ($ϵ/4$)	75.6	83.9	90.3	95.5	97.4
	Global ($ϵ/2$)	78.2	85.1	97.1	99.0	98.4
	R3 ($ϵ\times 2$)	70.2	80.0	81.5	87.4	97.4
	R3 ($ϵ\times 4$)	70.9	78.7	78.7	74.8	97.3
ResNet34	Global ($ϵ/4$)	53.6	74.2	74.3	79.5	88.4
	Global ($ϵ/2$)	68.4	84.7	87.8	92.1	96.4
	R3 ($ϵ\times 2$)	73.7	87.1	80.7	87.9	93.8
	R3 ($ϵ\times 4$)	76.2	88.4	87.3	89.6	97.5
VGG16	Global ($ϵ/4$)	65.4	63.7	87.1	76.8	94.1
	Global ($ϵ/2$)	54.0	54.7	94.7	83.9	94.3
	R3 ($ϵ\times 2$)	68.5	55.5	83.6	81.6	93.9
	R3 ($ϵ\times 4$)	67.0	55.2	85.7	86.3	94.0

Note: The best results are bolded.

.

As shown in Table 7, the proposed ED and FED methods showed stable performance for different scales of AEs on DenseNet121. On ResNet34, the performance of all detection methods exposed degradation as the perturbation scale decreased, indicating that AEs with a small perturbation scale had less difference with clean samples in both the feature space and the output space. On VGG16, our ED method showed relatively weak performance, while the FED method achieved high performance again after fine-tuning, which exhibited the plasticity of the model’s energy surface.

4.9. Robustness to Adaptive Attacks

An adaptive attack assumes that the attacker knows the specific strategy of the defender and modifies the original attack objective according to the defense objective. Usually, the attack successful rate (ASR) of an adaptive attack will decrease compared with the original attack under the same experimental settings. The more ASR falls, the harder the defense is to break. In this section, we assumed that the attacker knows that the victim model adopts an energy-based defense strategy (Equation (19)) and adds an energy regular term to the attack objective of FGSM (Equation (4)) and BIM (Equation (5)), that is

$${\eta }_{FGSM\_adp}\left(x\right)=sign\left({\nabla }_x\left[Loss\left(f\right(x),y)-\lambda ·E\left(x\right)\right]\right)$$

(24)

$${\eta }_{BIM\_adp}\left(x_{i+1}\right)=sign\left({\nabla }_x\left[Loss(f\left(x_i\right),y)-\lambda ·E\left(x\right)\right]\right)$$

(25)

The value of the weight parameter $\lambda$ was taken as 0.1, which is the same as that in Section 4.2.

As shown in

Table 8. Comparison of ASR between original attacks and adaptive attacks (%).

Attack		FGSM		BIM
		Original	Adaptive	Original	Adaptive
Network	DenseNet121	93.1	2.52	100	3.76
	ResNet34	96.0	2.40	97.3	2.44
	VGG16	97.8	8.52	99.1	8.66

Note: A lower ASR of adaptive attack indicates the greater robustness of defense.

, compared with their original versions, the ASR of adaptive AEs was greatly reduced (less than the detection threshold of 10%), which shows that the proposed method has a preliminary ability to resist adaptive attacks.

5. Discussion

Over the past few years, research on SAR adversarial attacks [8,9,30,31] mainly transferred the methods in optics without considering the special properties of SAR images. Adversarial perturbation added to the clean samples remains a high threat to the DNN classifier after being captured by the cameras [4], while the perturbation of SAR images is required to be coupled into the electromagnetic signals. Research on physically achievable SAR adversarial examples (AEs) has recently emerged, and current discussions focus on generating perturbations within a defined target region [17] and correlating digital perturbations with physical electromagnetic signals [18]. Aiming at the current hotspot of SAR adversarial attacks, we explored the security threats brought by region-constrained SAR AEs.

Through experiments, we found that current adversarial detection methods [14,15,16] degrade severely when solving the detection problem of region-constrained SAR AEs. In this paper, SAR AEs were regarded as unnatural low-probability samples, which expose higher energy than clean samples. By rejecting the high-energy inputs, the proposed ED and FED methods achieved more robust detection performance against SAR AEs with region-constrained perturbation. In addition, we also found that there was an inherent energy gap between the distributions of AEs and clean samples. From a thermodynamic point of view, high energy indicates a state of disorder. Hence, the essence of our methods is to reject high-entropy input and accept low-entropy input.

Meanwhile, we also found that the proposed method had relatively weak detection against BIM AEs and also suffered degradation against small-perturbation SAR AEs on the VGG16 network. In future work, we will improve our method on the generalization towards multiple AEs and the robustness towards perturbation scales.

6. Conclusions

In conclusion, this paper proposed an energy-based detector (ED) and a fine-tuned energy-based detector (FED) to solve the problem of detecting SAR AEs with region-constrained perturbation. Compared with the optical defense methods, the proposed methods significantly boosted the detection performance against SAR AEs, especially for those with regional constraints. Our research provides a foundational work for the future defense against physical SAR AEs.