Assessing Through-Water Structure-from-Motion Photogrammetry in Gravel-Bed Rivers under Controlled Conditions
Abstract
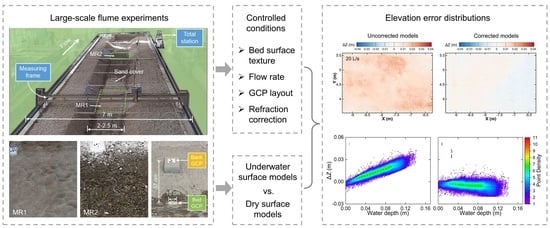
:1. Introduction
2. Methods
2.1. Flume Equipment
2.2. Experimental Design
2.3. Data Acquisition
2.4. Data Processing
3. Results
3.1. Error Statistics
3.2. Error Distributions
3.2.1. MR1
3.2.2. MR2
3.3. Error Variation with Water Depth
4. Discussions
4.1. Influence of Bed Texture
4.2. Influence of Flow Rate
4.3. Influence of GCP Layout and Refraction Correction
4.4. Limitations
- No GCPs were embedded into the bed surface in the downstream monitored reach, which made a direct comparison between the through-water SfM models using the bed GCPs for different bed textures impossible. A possible solution for future research is to first install the GCPs in the gravel bed surface, and then to release flows to the channel until the bed reaches equilibrium.
- Fine sediment transport occurred during the experiments. Since the surveyed reaches only took a small portion of the entire channel, there remained an accessible sediment supply from the upstream uncemented bed to the surveyed areas. As the influence of fine sediment transport is significant to the performance of through-water SfM, the fines should also be carefully controlled in the subsequent experiments on through-water SfM.
- The tested range of flow rate was limited. Although the smallest ratio between channel width and water depth reached 12.5 and 16.7 in MR1 and MR2, respectively, which were comparable or even smaller than previous field tests in gravel-bed rivers [5,34,38,57], the absolute water depths were smaller than most of the field investigations. If more efficient methods are available to keep all the bed materials static at higher flows in future, through-water SfM photogrammetry could be tested in large flumes, such as ours, under flow conditions fully comparable to those in the field.
- Since the camera angle could not be adjusted in our experiments, only nadir images were captured without any oblique imagery. The incorporation of oblique images into nadir-only image blocks has been reported to increase the precision and accuracy of SfM photogrammetry in dry areas [54,58]. Camera calibration [59] was not conducted in the SfM workflow in this study either, as it was difficult to strictly control the parameters in this procedure by the close-sourced algorithm in Metashape. Tests on the effects of oblique images and camera calibration on through-water SfM photogrammetry are still needed to further optimize this technique.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Workflow | Processing | Setting | |
|---|---|---|---|
| SfM | Add photos | Photo quality | >0.5 |
| Align images | Accuracy | Highest | |
| Generic preselection | Yes | ||
| Key point limit | 40,000 | ||
| Tie point limit | 4000 | ||
| Adaptive camera model fitting | No | ||
| Point colors | 3 bands, unit 16 | ||
| Georeference to GCPs | Projections | >10 | |
| Error (pix) | <0.5 | ||
| Build dense cloud | Quality | High | |
| Depth filtering | Mild | ||
| Calculate point colors | Yes | ||
| Build DEM | Source data | Dense cloud | |
| Interpolation | Disabled | ||
| Point classes | All | ||
| Build Orthomosaic | Resolution (m) | 0.00064 | |
| Blending mode | Mosaic | ||
| Surface | DEM | ||
| Hole filling | Yes | ||
| Refine seamlines | No | ||
| Refraction correction | Rasterize | Grid size | 0.005 m |
| Grid value | Minimum elevation | ||
| Export | Cloud | ||
| C2M Distance | Max distance | Disabled | |
| Signed distances | Yes | ||
| Filter submerged area | C2M Distance (m) | ≤0 | |
| pyBathySfM | Refractive Index | 1.333 | |
| Sensor length (mm) | 22.3 | ||
| Sensor width (mm) | 14.9 |
| Sub-Reach | Q (L/s) | Total Grid Number | Removed Point Number | Removed Point Number/Total Grid Number |
|---|---|---|---|---|
| Upstream | 20 | 278,940 | 16 | 0.006% |
| 40 | 284,277 | 5 | 0.002% | |
| 60 | 285,885 | 620 | 0.217% | |
| 100 | 287,456 | 6562 | 2.283% | |
| 120 | 287,929 | 26,063 | 9.052% | |
| Downstream | 20 | 251,850 | 8 | 0.003% |
| 40 | 255,440 | 184 | 0.072% | |
| 60 | 255,440 | 257 | 0.101% | |
| 100 | 255,440 | 3009 | 1.178% | |
| 120 | 255,440 | 3895 | 1.525% |






References
- Aberle, J.; Nikora, V. Statistical Properties of Armored Gravel Bed Surfaces. Water Resour. Res. 2006, 42, W11414. [Google Scholar] [CrossRef]
- Bailly, J.-S.; Coarer, Y.L.; Languille, P.; Stigermark, C.-J.; Allouis, T. Geostatistical Estimations of Bathymetric LiDAR Errors on Rivers. Earth Surf. Proc. Landf. 2010, 35, 1199–1210. [Google Scholar] [CrossRef]
- Mao, L.; Cooper, J.R.; Frostick, L.E. Grain Size and Topographical Differences between Static and Mobile Armour Layers. Earth Surf. Proc. Landf. 2011, 36, 1321–1334. [Google Scholar] [CrossRef]
- Brenna, A.; Surian, N.; Mao, L. Response of A Gravel—Bed River to Dam Closure: Insights from Sediment Transport Processes and Channel Morphodynamics. Earth Surf. Proc. Landf. 2020, 45, 756–770. [Google Scholar] [CrossRef]
- Helm, C.; Hassan, M.A.; Reid, D. Characterization of Morphological Units in a Small, Forested Stream Using Close-Range Remotely Piloted Aircraft Imagery. Earth Surf. Dynam. 2020, 8, 913–929. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Buffington, J.M. Channel-Reach Morphology in Mountain Drainage Basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]
- Hassan, M.A.; Church, M. Experiments on Surface Structure and Partial Sediment Transport on a Gravel Bed. Water Resour. Res. 2000, 36, 1885–1895. [Google Scholar] [CrossRef]
- Strom, K.; Papanicolaou, A.N.; Evangelopoulos, N.; Odeh, M. Microforms in Gravel Bed Rivers: Formation, Disintegration, and Effects on Bedload Transport. J. Hydraul. Eng. 2004, 130, 554–567. [Google Scholar] [CrossRef]
- Curran, J.C.; Tan, L. Effect of Bed Sand Content on the Turbulent Flows Associated with Clusters on an Armored Gravel Bed Surface. J. Hydraul. Eng. 2014, 140, 137–148. [Google Scholar] [CrossRef]
- Hassan, M.A.; Saletti, M.; Zhang, C.; Ferrer-Boix, C.; Johnson, J.P.L.; Müller, T.; Flotow, C. Co-Evolution of Coarse Grain Structuring and Bed Roughness in Response to Episodic Sediment Supply in an Experimental Aggrading Channel. Earth Surf. Proc. Landf. 2020, 45, 948–961. [Google Scholar] [CrossRef]
- Hassan, M.A.; Saletti, M.; Johnson, J.P.L.; Ferrer-Boix, C.; Venditti, J.G.; Church, M. Experimental Insights into the Threshold of Motion in Alluvial Channels: Sediment Supply and Streambed State. J. Geophys. Res.-Earth 2020, 125, e2020JF005736. [Google Scholar] [CrossRef]
- Wohl, E.; Lane, S.N.; Wilcox, A.C. The Science and Practice of River Restoration. Water Resour. Res. 2015, 51, 5974–5997. [Google Scholar] [CrossRef] [Green Version]
- Wohl, E. Connectivity in Rivers. Prog. Phys. Geog. 2017, 41, 345–362. [Google Scholar] [CrossRef]
- Muhlfeld, C.C.; Dauwalter, D.C.; Kovach, R.P.; Kershner, J.L.; Williams, J.E.; Epifanio, J. Trout in Hot Water: A Call for Global Action. Science 2018, 360, 866–867. [Google Scholar] [CrossRef]
- Wang, J.; Hassan, M.A.; Saletti, M.; Chen, X.; Fu, X.; Zhou, H.; Yang, X. On How Episodic Sediment Supply Influences the Evolution of Channel Morphology, Bedload Transport and Channel Stability in an Experimental Step-Pool Channel. Water Resour. Res. 2021, 57, e2020WR029133. [Google Scholar] [CrossRef]
- Sandoval, J.; Mignot, E.; Mao, L.; Pastén, P.; Bolster, D.; Escauriaza, C. Field and Numerical Investigation of Transport Mechanisms in a Surface Storage Zone. J. Geophys. Res.-Earth 2019, 124, 938–959. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; DiBiase, R.A.; McCarroll, N.; Liu, X. Quantifying Flow Resistance in Mountain Streams Using Computational Fluid Dynamics Modeling over Structure-from-Motion Photogrammetry-Derived Microtopography. Earth Surf. Proc. Landf. 2019, 44, 1973–1987. [Google Scholar] [CrossRef]
- Chen, Y.; Bao, J.; Fang, Y.; Perkins, W.A.; Ren, H.; Song, X.; Duan, Z.; Hou, Z.; He, X.; Scheibe, T.D. Modeling of Streamflow in a 30 Km Long Reach Spanning 5 Years Using OpenFOAM 5.x. Geosci. Model Dev. 2022, 15, 2917–2947. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Hassan, M.A.; Xu, M.; He, P. Hybrid Modeling on 3D Hydraulic Features of a Step-Pool Unit. Earth Surf. Dynam. 2022. preprint. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-Based Surface Reconstruction in Geomorphometry—Merits, Limits and Developments. Earth Surf. Dynam. 2016, 4, 359–389. [Google Scholar] [CrossRef] [Green Version]
- Leduc, P.; Peirce, S.; Ashmore, P. Short Communication: Challenges and Applications of Structure-from-Motion Photogrammetry in a Physical Model of a Braided River. Earth Surf. Dynam. 2019, 7, 97–106. [Google Scholar] [CrossRef] [Green Version]
- Tmušić, G.; Manfreda, S.; Aasen, H.; James, M.R.; Gonçalves, G.; Ben-Dor, E.; Brook, A.; Polinova, M.; Arranz, J.J.; Mészáros, J.; et al. Current Practices in UAS-Based Environmental Monitoring. Remote Sens. 2020, 12, 1001. [Google Scholar] [CrossRef] [Green Version]
- Javernick, L.; Brasington, J.; Caruso, B. Modeling the Topography of Shallow Braided Rivers Using Structure-from-Motion Photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Morgan, J.A.; Brogan, D.J.; Nelson, P.A. Application of Structure-from-Motion Photogrammetry in Laboratory Flumes. Geomorphology 2017, 276, 125–143. [Google Scholar] [CrossRef] [Green Version]
- Verma, A.K.; Bourke, M.C. A Method Based on Structure-from-Motion Photogrammetry to Generate Sub-Millimetre-Resolution Digital Elevation Models for Investigating Rock Breakdown Features. Earth Surf. Dynam. 2019, 7, 45–66. [Google Scholar] [CrossRef] [Green Version]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- James, M.R.; Chandler, J.H.; Eltner, A.; Fraser, C.; Miller, P.E.; Mills, J.P.; Noble, T.; Robson, S.; Lane, S.N. Guidelines on the Use of Structure-from-Motion Photogrammetry in Geomorphic Research. Earth Surf. Proc. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Cucchiaro, S.; Cavalli, M.; Vericat, D.; Crema, S.; Llena, M.; Beinat, A.; Marchi, L.; Cazorzi, F. Monitoring Topographic Changes through 4D-Structure-from-Motion Photogrammetry: Application to a Debris-Flow Channel. Environ. Earth Sci. 2018, 77, 632. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, M.; Hassan, M.A.; Chartrand, S.M.; Wang, Z. Experimental Study on the Stability and Failure of Individual Step-Pool. Geomorphology 2018, 311, 51–62. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, M.; Hassan, M.A.; Chartrand, S.M.; Wang, Z.; Ma, Z. Experiment on Morphological and Hydraulic Adjustments of Step-Pool Unit to Flow Increase. Earth Surf. Proc. Landf. 2019, 45, 280–294. [Google Scholar] [CrossRef]
- Ravazzolo, D.; Spreitzer, G.; Friedrich, H.; Tunnicliffe, J. Flume Experiments on the Geomorphic Effects of Large Wood in Gravel-Bed Rivers. In Proceedings of the River Flow 2020, International Conference on Fluvial Hydraulics 2020, Online, 6–17 July 2020; CRC Press: Boca Raton, FL, USA, 2020; pp. 1609–1615. [Google Scholar]
- Piton, G.; Recking, A.; Coz, J.L.; Bellot, H.; Hauet, A.; Jodeau, M. Reconstructing Depth-Averaged Open-Channel Flows Using Image Velocimetry and Photogrammetry. Water Resour. Res. 2018, 54, 4164–4179. [Google Scholar] [CrossRef]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying Submerged Fluvial Topography Using Hyperspatial Resolution UAS Imagery and Structure from Motion Photogrammetry. Earth Surf. Proc. Landf. 2014, 40, 47–64. [Google Scholar] [CrossRef] [Green Version]
- van Scheltinga, R.C.T.; Coco, G.; Kleinhans, M.G.; Friedrich, H. Observations of Dune Interactions from DEMs Using Through-Water Structure from Motion. Geomorphology 2020, 359, 107126. [Google Scholar] [CrossRef]
- David, C.G.; Kohl, N.; Casella, E.; Rovere, A.; Ballesteros, P.; Schlurmann, T. Structure-from-Motion on Shallow Reefs and Beaches: Potential and Limitations of Consumer-Grade Drones to Reconstruct Topography and Bathymetry. Coral Reefs 2021, 40, 835–851. [Google Scholar] [CrossRef]
- Lane, S.N.; Widdison, P.E.; Thomas, R.E.; Ashworth, P.J.; Best, J.L.; Lunt, I.A.; Smith, G.H.S.; Simpson, C.J. Quantification of Braided River Channel Change Using Archival Digital Image Analysis. Earth Surf. Proc. Landf. 2010, 35, 971–985. [Google Scholar] [CrossRef]
- Dietrich, J.T. Bathymetric Structure-from-Motion: Extracting Shallow Stream Bathymetry from Multi-View Stereo Photogrammetry. Earth Surf. Proc. Landf. 2016, 42, 355–364. [Google Scholar] [CrossRef]
- Shintani, C.; Fonstad, M.A. Comparing Remote-Sensing Techniques Collecting Bathymetric Data from a Gravel-Bed River. Int. J. Remote Sens. 2017, 38, 2883–2902. [Google Scholar] [CrossRef]
- Wilson, R.; Harrison, S.; Reynolds, J.; Hubbard, A.; Glasser, N.F.; Wündrich, O.; Anacona, P.I.; Mao, L.; Shannon, S. The 2015 Chileno Valley Glacial Lake Outburst Flood, Patagonia. Geomorphology 2019, 332, 51–65. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Karantzalos, K.; Georgopoulos, A.; Skarlatos, D. Correcting Image Refraction: Towards Accurate Aerial Image-Based Bathymetry Mapping in Shallow Waters. Remote Sens. 2020, 12, 322. [Google Scholar] [CrossRef]
- Georgopoulos, A.; Agrafiotis, P. Documentation of a Submerged Monument Using Improved Two Media Techniques. In Proceedings of the 2012 IEEE 18th International Conference on Virtual Systems and Multimedia, Milan, Italy, 2–5 September 2012. [Google Scholar]
- Skarlatos, D.; Agrafiotis, P. A Novel Iterative Water Refraction Correction Algorithm for Use in Structure from Motion Photogrammetric Pipeline. J. Mar. Sci. Eng. 2018, 6, 77. [Google Scholar] [CrossRef] [Green Version]
- Mandlburger, G. Through-Water Dense Image Matching for Shallow Water Bathymetry. Photogramm. Eng. Remote Sens. 2019, 85, 445–455. [Google Scholar] [CrossRef]
- Dietrich, W.E.; Kirchner, J.W.; Ikeda, H.; Iseya, F. Sediment Supply and the Development of the Coarse Surface Layer in Gravel-Bedded Rivers. Nature 1989, 340, 215–217. [Google Scholar] [CrossRef]
- Weichert, R.B.; Bezzola, G.R.; Minor, H.-E. Bed Morphology and Generation of Step-Pool Channels. Earth Surf. Proc. Landf. 2008, 33, 1678–1692. [Google Scholar] [CrossRef]
- Roy, A.G.; Buffin-Blanger, T.; Lamarre, H.; Kirkbride, A.D. Size, Shape and Dynamics of Large-Scale Turbulent Flow Structures in a Gravel-Bed River. J. Fluid Mech. 2004, 500, 1–27. [Google Scholar] [CrossRef] [Green Version]
- James, M.R.; Robson, S.; dOleire-Oltmanns, S.; Niethammer, U. Optimising UAV Topographic Surveys Processed with Structure-from-Motion: Ground Control Quality, Quantity and Bundle Adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; di Cella, U.M.; Roncella, R.; Santise, M. Quality Assessment of DSMs Produced from UAV Flights Georeferenced with On-Board RTK Positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef] [Green Version]
- Manfreda, S.; Dvorak, P.; Mullerova, J.; Herban, S.; Vuono, P.; Justel, J.A.; Perks, M. Assessing the Accuracy of Digital Surface Models Derived from Optical Imagery Acquired with Unmanned Aerial Systems. Drones 2019, 3, 15. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y. Study of the Resistance Structure of Gravel Bed in Wide Shallow Channel. Master’s Thesis, Tsinghua University, Beijing, China, 2015. (In Chinese with English abstract). [Google Scholar]
- Detert, M.; Weitbrecht, V. Automatic Object Detection to Analyze the Geometry of Gravel Grains—A Free Stand-Alone Tool. In Proceedings of the River Flow 2012, International Conference on Fluvial Hydraulics 2012, San José, CA, USA, 5–7 September 2012; CRC Press: Boca Raton, FL, USA, 2012; pp. 595–600. [Google Scholar]
- Huang, K.; Zhang, C.; Xu, M.; Lin, Y. Application study on the automated grain sizing based on BASEGRAIN software. J. Sediment Res. 2020, 45, 44–51, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- James, M.R.; Antoniazza, G.; Robson, S.; Lane, S.N. Mitigating Systematic Error in Topographic Models for Geomorphic Change Detection: Accuracy, Precision and Considerations beyond off-Nadir Imagery. Earth Surf. Proc. Landf. 2020, 45, 2251–2271. [Google Scholar] [CrossRef]
- Dietrich, J.T. Py\_sfm\_depth Homepage. Available online: https://www.geojames.github.io/py_sfm_depth (accessed on 3 June 2020).
- Wang, H.; Zhong, Q.; Wang, X.; Li, D. Quantitative Characterization of Streaky Structures in Open-Channel Flows. J. Hydraul. Eng. 2017, 143, 04017040. [Google Scholar] [CrossRef]
- Detert, M.; Johnson, E.D.; Weitbrecht, V. Proof-of-Concept for Low-Cost and Non-Contact Synoptic Airborne River Flow Measurements. Int. J. Remote Sens. 2017, 38, 2780–2807. [Google Scholar] [CrossRef]
- Nesbit, P.; Hugenholtz, C. Enhancing UAV–SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
- Shortis, M. Camera Calibration Techniques for Accurate Measurement Underwater. In 3D Recording and Interpretation for Maritime Archaeology; Coastal Research Library, McCarthy, J., Benjamin, J., Winton, T., van Duivenvoorde, W., Eds.; Springer: Cham, Switzerland, 2019; Volume 31, pp. 11–28. [Google Scholar]











| Reach | Bed Texture | Cement | Analyzed Length (cm) | Analyzed Width (cm) | Grid No. | Bed GCP | Bank GCP | ||
|---|---|---|---|---|---|---|---|---|---|
| No. | Mean Height (cm) | No. | Mean Height (cm) | ||||||
| MR1 | Fine sand | Bed and bank | 360 | 200 | 288,000 | 6 | 0 | 6 | 37 |
| MR2 | Gravel | Bank | 310 | 206 | 255,440 | 4 | 7 | 4 | 42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Sun, A.; Hassan, M.A.; Qin, C. Assessing Through-Water Structure-from-Motion Photogrammetry in Gravel-Bed Rivers under Controlled Conditions. Remote Sens. 2022, 14, 5351. https://doi.org/10.3390/rs14215351
Zhang C, Sun A, Hassan MA, Qin C. Assessing Through-Water Structure-from-Motion Photogrammetry in Gravel-Bed Rivers under Controlled Conditions. Remote Sensing. 2022; 14(21):5351. https://doi.org/10.3390/rs14215351
Chicago/Turabian StyleZhang, Chendi, Ao’ran Sun, Marwan A. Hassan, and Chao Qin. 2022. "Assessing Through-Water Structure-from-Motion Photogrammetry in Gravel-Bed Rivers under Controlled Conditions" Remote Sensing 14, no. 21: 5351. https://doi.org/10.3390/rs14215351
APA StyleZhang, C., Sun, A., Hassan, M. A., & Qin, C. (2022). Assessing Through-Water Structure-from-Motion Photogrammetry in Gravel-Bed Rivers under Controlled Conditions. Remote Sensing, 14(21), 5351. https://doi.org/10.3390/rs14215351