BDS and Galileo: Global Ionosphere Modeling and the Comparison to GPS and GLONASS
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data
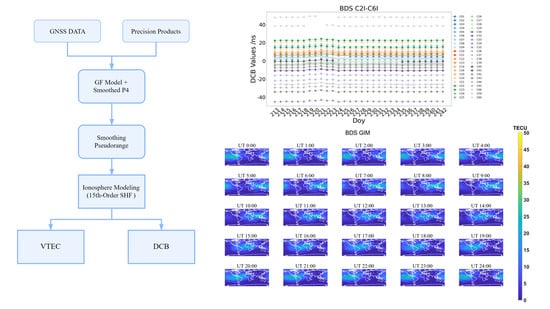
2.2. Ionospheric TEC Modeling and DCB Estimation
2.3. Evaluation Methodology
3. Results and Analysis
3.1. IPP Distribution
3.2. Validation of Ionosphere Estimation Algorithm
3.2.1. Accuracy of Ionosphere Model in Quiet Day
3.2.2. Accuracy of Ionosphere Model in Active Day
3.2.3. Analysis of Ionospheric Outliers
3.3. Validation of DCB Estimation Algorithm
3.3.1. Accuracy of GPS and GLONASS DCB
3.3.2. Accuracy of Galileo DCB
3.3.3. Accuracy of BDS DCB
3.3.4. Accuracy of Other Frequency DCB Type
4. Discussion
5. Conclusions
- The IPPs of GPS and GLONASS are abundant and globally distributed. With the construction and development of Galileo and BDS, Galileo and BDS IPPs cover the global continents. However, Galileo and BDS IPPs are less than that of GPS and GLONASS, which is mainly due to the limited number of stations.
- GPS and GLONASS ionospheric models with greater accuracy, followed by Galileo. Although BDS is limited by the number of stations and has the lowest number of IPPs of the four systems, the ionospheric model built still performs well.
- The orbit characteristics of the BDS GEO satellite make its IPPs a point above the earth. When IPPs are abundant, it does not play an obvious role in ionosphere modeling.
- Some grid points will be negative in the ionospheric modeling results, which will be assigned as 0 in this manuscript, and the number and proportion at the latitude will be counted. The 0-value region is mainly distributed in the middle and high latitude regions of the southern hemisphere. The 0-value area of BDS is larger than that of the other systems.
- GPS, GLONASS, Galileo, BDS MEO and IGSO satellite DCB show better stability, while the BDS GEO satellite has low stability due to poor data quality. Comparing the estimated satellite DCB with other institutions, the DCB estimated in this manuscript has good consistency. The average biases of the four systems are basically within 0.25 ns, 0.25 ns, 0.2 ns and 0.42 ns, and the STD is basically within 0.25 ns. The consistency of DCB of the BDS-3 satellite is better than that of the BDS-2 satellite. Other DCB types of these systems show stability and consistency with other institutions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haddad, R.; Kovach, K.; Slattery, R. GPS modernization and beyond/2020 IEEE/ION Position, Location and Navigation Symposium (PLANS). IEEE 2020, 399–406. Available online: https://ieeexplore.ieee.org/abstract/document/9110167 (accessed on 12 October 2022).
- Thomas, M.L. Evolution of GPS systems architecture and its impacts. Commun. IIMA 2010, 10, 3. [Google Scholar]
- Fontana, R.; Latterman, D. GPS Modernization and the Future. In Proceedings of the IAIN World Congress and the 56th Annual Meeting of The Institute of Navigation (2000), San Diego, CA, USA, 26–28 June 2000; pp. 222–231. [Google Scholar]
- Thoelert, S.; Steigenberger, P.; Montenbruck, O. Signal analysis of the first GPS III satellite. GPS Solut. 2019, 23, 92. [Google Scholar] [CrossRef]
- Paziewski, J. Recent advances and perspectives for positioning and applications with smartphone GNSS observations. Meas. Sci. Technol. 2020, 31, 091001. [Google Scholar] [CrossRef]
- Priyanka, C.; Ratnam, D.V.; Sai, K.S.G. A Review on design of low noise amplifiers for global navigational satellite system. AIMS Electron. Electr. Eng. 2021, 5, 206–229. [Google Scholar] [CrossRef]
- Julien, O.; Priya, L.; Issler, J.L. Estimating the ionospheric delay using GPS/Galileo signals in the E5 band. Inside GNSS 2015, 10, 55–64. [Google Scholar]
- Li, M.; Yuan, Y. Estimation and Analysis of BDS2 and BDS3 Differential Code Biases and Global Ionospheric Maps Using BDS Observations. Remote Sens 2021, 13, 370. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, L.; Li, J.; Yang, Y.; Zhang, T.; Mao, Y.; Sun, B.; Ren, X. Featured services and performance of BDS-3. Sci. Bull. 2021, 66, 2135–2143. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.U.; Wang, J.L. Electron density profiles derived from ground-based GPS observations. J. Navig. 2006, 59, 395–401. [Google Scholar] [CrossRef] [Green Version]
- Isioye, O.A.; Combrinck, L.; Botai, J.O.; Munghemezulu, C. The potential for observing African weather with GNSS remote sensing. Adv. Meteorol. 2015, 2015, 723071. [Google Scholar] [CrossRef] [Green Version]
- Hegarty, C.J.; Chatre, E. Evolution of the global navigation satellite system (gnss). Proc. IEEE 2008, 96, 1902–1917. [Google Scholar] [CrossRef]
- Wang, H.; Hou, Y.; Dang, Y.; Bei, J.; Zhang, Y.; Wang, J.; Cheng, Y.; Gu, S. Long-term time-varying characteristics of UPD products generated by a global and regional network and their interoperable application in PPP. Adv. Space Res. 2021, 67, 883–901. [Google Scholar] [CrossRef]
- Wang, H.; Dang, Y.; Hou, Y.; Bei, J.; Wang, J.; Bai, G.; Cheng, Y.; Zhang, S. Rapid and precise solution of the whole network of thousands of stations in China based on PPP network solution by UPD fixed technology. Acta Geod. Cart. 2020, 49, 278–291. [Google Scholar]
- Ma, H.; Zhao, Q.; Verhagen, S. Assessing the performance of multi-GNSS PPP-RTK in the local area. Remote Sens. 2020, 12, 3343. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Lu, X. Interactive multiple-model vertical vibration detection of structures based on high-frequency GNSS observations. GPS Solut. 2022, 26, 1–19. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Chen, R. Displacement detection based on Bayesian inference from GNSS kinematic positioning for deformation monitoring. Mech. Syst. Signal. Pract. 2022, 167, 108570. [Google Scholar] [CrossRef]
- Xu, X.; Li, M.; Li, W.; Liu, J. Performance Analysis of Beidou-2/Beidou-3e Combined Solution with Emphasis on Precise Orbit Determination and Precise Point Positioning. Sensors 2018, 18, 135. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Wang, X.; Liu, J.; Zhao, Q. Characteristics of BD3 Global Service Satellites: POD, Open Service Signal and Atomic Clock Performance. Remote Sens. 2019, 11, 1559. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.; Psychas, D.; Xing, X. Influence of the inhomogeneous troposphere on GNSS positioning and integer ambiguity resolution. Adv. Space Res. 2021, 67, 1914–1928. [Google Scholar] [CrossRef]
- Ma, H.; Verhagen, S. Precise point positioning on the reliable detection of tropospheric model errors. Sensors 2020, 20, 1634. [Google Scholar] [CrossRef] [Green Version]
- Psychas, D.; Bruno, J.; Massarweh, L. Towards sub-meter positioning using Android raw GNSS measurements. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3917–3931. [Google Scholar]
- Ma, H.; Verhagen, S.; Psychas, D.; Monico, J.F.G.; Marques, H.A. Flight-test evaluation of integer ambiguity resolution enabled PPP. J. Surv. Eng. 2021, 147, 04021013. [Google Scholar] [CrossRef]
- Seok, H.W.; Ansari, K.; Panachai, C. Individual performance of multi-GNSS signals in the determination of STEC over Thailand with the applicability of Klobuchar model. Adv. Space Res. 2022, 69, 1301–1318. [Google Scholar] [CrossRef]
- Wilson, B.D.; Mannucci, A.J. Instrumental biases in ionospheric measurements derived from GPS data. In Proceedings of the ION GPS 1993 (Institute of Navigation), Salt Lake City, UT, USA, 22–24 September 1993; pp. 1343–1351. [Google Scholar]
- Davis, J.L.; Cosmo, M.L.; Elgered, G. Using the Global Positioning System to study the atmosphere of the Earth: Overview and prospects. GPS Trends Precise Terr. Airborne Spaceborne Appl. 1996, 233–242. Available online: https://linkspringer.53yu.com/chapter/10.1007/978-3-642-80133-4_37 (accessed on 12 October 2022).
- Komjathy, A.; Yang, Y.M.; Meng, X. Review and perspectives: Understanding natural-hazards-generated ionospheric perturbations using GPS measurements and coupled modeling. Radio Sci. 2016, 51, 951–961. [Google Scholar] [CrossRef]
- Panda, S.K.; Haralambous, H.; Moses, M. Ionospheric and plasmaspheric electron contents from space-time collocated digisonde, COSMIC, and GPS observations and model assessments. Acta Astronaut. 2021, 179, 619–635. [Google Scholar] [CrossRef]
- Marković, M. Determination of total electron content in the ionosphere using GPS technology. Geonauka 2014, 2, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wang, C.; Wang, J.X. Global characteristics of the second-order ionospheric delay error using inversion of electron density profiles from COSMIC occultation data. Sci. China Phys. Mech. 2014, 57, 365–374. [Google Scholar] [CrossRef]
- Brunini, C.; Azpilicueta, F. GPS slant total electron content accuracy using the single layer model under different geomagnetic regions and ionospheric conditions. J. Geod. 2010, 84, 293–304. [Google Scholar] [CrossRef]
- Wang, X.L.; Wan, Q.T.; Ma, G.Y. The influence of ionospheric thin shell height on TEC retrieval from GPS observation. Res. Astron. Astrophys. 2016, 16, 016. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, Z.; Zhang, H. Comparison and Consistency Research of Regional Ionospheric TEC Models Based on GPS Measurements. Geomat. Inf. Ence Wuhan Univ. 2008, 33, 479–483. [Google Scholar]
- Zhang, H.; Han, W.; Huang, L. Modeling global ionospheric delay with IGS ground-based GNSS observations. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 1186–1189. [Google Scholar]
- Shagimuratov, I.I.; Chernyak, Y.V.; Zakharenkova, I.E. Use of GLONASS for studying the ionosphere. Russ. J. Phys. Chem. B+ 2015, 9, 770–777. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Mylnikova, A.A.; Polyakova, A.S. Estimating the total electron content absolute value from the GPS/GLONASS data. Results Phys. 2015, 5, 32–33. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xie, W.; Ren, X. Influence of the GLONASS inter-frequency bias on differential code bias estimation and ionospheric modeling. GPS Solut. 2017, 21, 1355–1367. [Google Scholar] [CrossRef]
- Xue, J.; Song, S.; Liao, X. Estimating and assessing Galileo navigation system satellite and receiver differential code biases using the ionospheric parameter and differential code bias joint estimation approach with multi-GNSS observations. Radio Sci. 2016, 51, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Bidaine, B.; Warnant, R. Ionosphere modeling for Galileo single frequency users: Illustration of the combination of the NeQuick model and GNSS data ingestion. Adv. Space Res. 2011, 47, 312–322. [Google Scholar] [CrossRef] [Green Version]
- Hernández-Pajares, M.; Lyu, H.; Garcia-Fernandez, M. A new way of improving global ionospheric maps by ionospheric tomography: Consistent combination of multi-GNSS and multi-space geodetic dual-frequency measurements gathered from vessel-, LEO-and ground-based receivers. J. Geod. 2020, 94, 1–16. [Google Scholar] [CrossRef]
- Zhang, M. Establishment of European Regional Ionosphere Model Based on Spherical Harmonic Functions. J. World Archit. 2021, 5, 5–9. [Google Scholar] [CrossRef]
- Le, A.Q. Impact of Galileo on global ionosphere map estimation. J. Navig. 2006, 59, 281–292. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhang, B.; Yuan, Y. Single-frequency precise point positioning (PPP) for retrieving ionospheric TEC from BDS B1 data. GPS Solut 2019, 23, 1–11. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X. Multi-GNSS contributions to differential code biases determination and regional ionospheric modeling in China. Adv. Space Res. 2020, 65, 221–234. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, X.; Xie, W. Global ionospheric modeling using multi-GNSS: BeiDou, Galileo, GLONASS and GPS. Sci. Rep. 2016, 6, 33499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, R.; Jin, S.; Feng, G. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2. User Manual, Astronomical Institute; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Z.; Yang, Z. A Refined Metric for Multi-GNSS Constellation Availability Assessment in Polar Regions. Adv. Space Res. 2020, 4, 33. [Google Scholar] [CrossRef]


























| Area | GPS | GLONASS | Galileo | BDS | BDS (MEO + IGSO) |
|---|---|---|---|---|---|
| NH | 0.05 | 1.32 | 6.78 | 40.36 | 42.22 |
| NM | 0.01 | 1.08 | 8.38 | 49.83 | 45.06 |
| NL | 0.10 | 0.13 | 0.17 | 5.08 | 4.67 |
| SL | 0.04 | 0.12 | 3.42 | 22.8 | 30.24 |
| SM | 82.97 | 114.31 | 156.99 | 328.87 | 406.42 |
| SH | 233.93 | 217.96 | 346.6 | 691.72 | 680.57 |
| Area | GPS | GLONASS | Galileo | BDS | BDS (MEO + IGSO) |
|---|---|---|---|---|---|
| NH | 0.66 | 1.33 | 2.69 | 59.96 | 59.86 |
| NM | 0.47 | 1.62 | 2.78 | 51.02 | 52.65 |
| NL | 0.04 | 0.11 | 0.13 | 3.22 | 2.70 |
| SL | 0.01 | 0.00 | 0.24 | 10.49 | 13.89 |
| SM | 15.23 | 14.81 | 17.67 | 113.58 | 139.07 |
| SH | 12.23 | 11.54 | 21.94 | 187.99 | 169.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, H.; Dang, Y.; Ma, H.; Xu, C.; Yang, Q.; Ren, Y.; Fang, S. BDS and Galileo: Global Ionosphere Modeling and the Comparison to GPS and GLONASS. Remote Sens. 2022, 14, 5479. https://doi.org/10.3390/rs14215479
Wang Y, Wang H, Dang Y, Ma H, Xu C, Yang Q, Ren Y, Fang S. BDS and Galileo: Global Ionosphere Modeling and the Comparison to GPS and GLONASS. Remote Sensing. 2022; 14(21):5479. https://doi.org/10.3390/rs14215479
Chicago/Turabian StyleWang, Yafeng, Hu Wang, Yamin Dang, Hongyang Ma, Changhui Xu, Qiang Yang, Yingying Ren, and Shushan Fang. 2022. "BDS and Galileo: Global Ionosphere Modeling and the Comparison to GPS and GLONASS" Remote Sensing 14, no. 21: 5479. https://doi.org/10.3390/rs14215479
APA StyleWang, Y., Wang, H., Dang, Y., Ma, H., Xu, C., Yang, Q., Ren, Y., & Fang, S. (2022). BDS and Galileo: Global Ionosphere Modeling and the Comparison to GPS and GLONASS. Remote Sensing, 14(21), 5479. https://doi.org/10.3390/rs14215479