Analysis and Correction of the Rolling Shutter Effect for a Star Tracker Based on Particle Swarm Optimization
Abstract
:1. Introduction
2. Materials and Methods
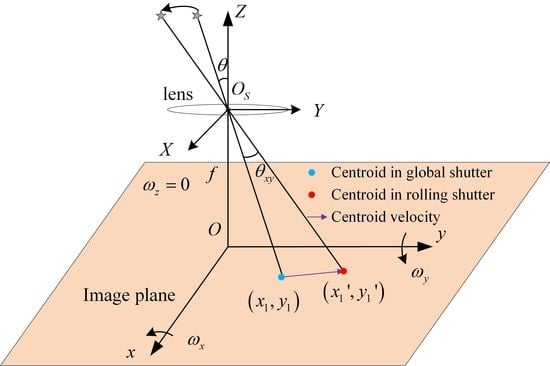
2.1. Velocity Model
2.2. Installation Mode Design
2.3. Installation Mode Particle Swarm Optimization
| Algorithm 1 Standard PSO pseudocode |
| 1: Algorithm input: particle number , the maximum number of iterations N, inertia angular velocity |
| 2: Algorithm output: optimal angular velocity , the loss function |
| 3: Randomly generate velocity solutions |
| 4: g = 0 |
| 5: while g < N do |
| 6: for i = 1 to do |
| 7: |
| 8: |
| 9: end for |
| 10: computer fitness function value |
| 11: |
| 12: Find the best solution in all the particles in the iteration |
| 13: if |
| 14: |
| 15: else |
| 16: |
| 17: n = n + 1 |
| 18: end |
3. Results
3.1. Simulation of Star Centroid Velocity with Collinear Installation
3.2. Simulation Experiment
3.2.1. Convergence Simulation
3.2.2. Robustness of the Algorithm under Different Angular Velocities and Different Position Noise
3.3. Field Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.D.; Du, L.; Li, Y.C.; Lyu, G.X.; Chen, B. Attitude and Size Estimation of Satellite Targets Based on ISAR Image Interpretation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5109015. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chen, C.Y.; Wang, G.Y.; Wei, X.G. Parameters Estimation of Nutational Satellite Based on Sun Sensor. IEEE Trans. Instrum. Meas. 2022, 71, 7000508. [Google Scholar] [CrossRef]
- Kouyama, T.; Kanemura, A.; Kato, S.; Imamoglu, N.; Fukuhara, T.; Nakamura, R. Satellite Attitude Determination and Map Projection Based on Robust Image Matching. Remote Sens. 2017, 9, 90. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.M.; Chen, R.T.; Weng, J. A super-fast optimal attitude matrix in attitude determination. Meas. Sci. Technol. 2021, 32, 095012. [Google Scholar] [CrossRef]
- Ding, J.; Dai, D.; Tan, W.; Wang, X.; Qin, S. Implementation of a real-time star centroid extraction algorithm with high speed and superior denoising ability. Appl. Opt. 2022, 61, 3115–3122. [Google Scholar] [CrossRef] [PubMed]
- Ni, Y.M.; Wang, X.S.; Dai, D.K.; Tan, W.F.; Qin, S.Q. Adaptive section non-uniformity correction method of short-wave infrared star images for a star tracker. Appl. Opt. 2022, 61, 6992–6999. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wang, M.; Zhu, Y.; Long, X.X. Low frequency error analysis and calibration for multiple star sensors system of GaoFen7 satellite. Geo-Spat. Inf. Sci. 2022. [Google Scholar] [CrossRef]
- McKee, P.; Nguyen, H.; Kudenov, M.W.; Christian, J.A. StarNAV with a wide field-of-view optical sensor. Acta Astronaut. 2022, 197, 220–234. [Google Scholar] [CrossRef]
- Hancock, B.R.; Stirbl, R.C.; Cunningham, T.J.; Pain, B.; Wrigley, C.J.; Ringold, P.G. CMOS active pixel sensor specific performance effects on star tracker/imager position accuracy. In Proceedings of the Conference on Functional Integration of Opto-Electro-Mechanical Devices and Systems, San Jose, CA, USA, 24–25 January 2001; pp. 43–53. [Google Scholar]
- Liang, C.K.; Chang, L.W.; Chen, H.H. Analysis and compensation of rolling shutter effect. IEEE Trans. Image Process. 2008, 17, 1323–1330. [Google Scholar] [CrossRef] [Green Version]
- He, Z.-Y.; Wei, P. New method for 2D velocity measurement based on electronic rolling shutter. In Proceedings of the International Conference on Photoelectronic Detection and Imaging, Beijing, China, 9–12 September 2007. [Google Scholar]
- Rengarajan, V.; Balaji, Y.; Rajagopalan, A.N.; Ieee. Unrolling the Shutter: CNN to Correct Motion Distortions. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2345–2353.
- Wei, M.S.; Xing, F.; You, Z. An implementation method based on ERS imaging mode for sun sensor with 1 kHz update rate and 1″ precision level. Opt. Express 2013, 21, 32524–32533. [Google Scholar] [CrossRef]
- Zhang, B.-Y.; Kong, D.-Z.; Liu, J.-G.; Wu, X.-X.; Dong, D.-Y. Compensation of star image motion for a CMOS image sensor with a rolling shutter. Chin. Opt. 2020, 13, 1276–1284. [Google Scholar] [CrossRef]
- Enright, J.; Dzamba, T. Rolling Shutter Compensation for Star Trackers. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- He, L.; Zhao, R.; Ma, Y.; Hou, Y.; Zhu, Z.; Zeng, S. Navigation Stars Correction Method of Rolling Shutter Exposure Star Tracker Based on Time Domain Constraint. Acta Photonica Sin. 2021, 50, 128. [Google Scholar] [CrossRef]
- He, L.; Ma, Y.; Zhao, R.; Hou, Y.; Zhu, Z. High Update Rate Attitude Measurement Method of Star Sensors Based on Star Point Correction of Rolling Shutter Exposure. Sensors 2021, 21, 5724. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H. Single-Frame Rolling Shutter Corrector for Star Trackers. J. Spacecr. Rocket. 2019, 56, 292–297. [Google Scholar] [CrossRef]
- Schiattarella, V.; Spiller, D.; Curti, F. Star identification robust to angular rates and false objects with rolling shutter compensation. Acta Astronaut. 2020, 166, 243–259. [Google Scholar] [CrossRef]
- Li, Y.; Wei, X.; Li, J.; Wang, G. Error Correction of Rolling Shutter Effect for Star Sensor Based on Angular Distance Invariance Using Single Frame Star Image. IEEE Trans. Instrum. Meas. 2022, 71, 7003213. [Google Scholar] [CrossRef]
- Boussaid, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y.H. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Wang, X.; Tan, W.; Dai, D.; Qin, S. Error coupling analysis of the laboratory calibration method for a star tracker. Appl. Opt. 2021, 60, 2372–2379. [Google Scholar] [CrossRef]
- Zhang, C.F.; Niu, Y.X.; Zhang, H.; Lu, J.Z. Optimized star sensors laboratory calibration method using a regularization neural network. Appl. Opt. 2018, 57, 1067–1074. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Niu, Y.; Lu, J.; Zhang, C.; Yang, Y. On-orbit calibration for star sensors without priori information. Opt. Express 2017, 25, 18393–18409. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Yang, X.; Xu, T.; Fu, Z.; Chang, L.; Yang, C.; Jin, G. An End-to-End Identification Algorithm for Smearing Star Image. Remote Sens. 2021, 13, 4541. [Google Scholar] [CrossRef]
- Song, J.N.; Zhang, Z.X.; Iwasaki, A.; Wang, J.H.; Sun, J.; Sun, Y. An Augmented H-infinity Filter for Satellite Jitter Estimation Based on ASTER/SWIR and Blurred Star Images. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2637–2646. [Google Scholar] [CrossRef]
- Wang, F.; Xi, R.; Yue, C.; Li, H.; Cao, X. Conceptual rotational mode design for optical conical scanning imaging small satellites. Sci. China Technol. Sci. 2020, 63, 1383–1395. [Google Scholar] [CrossRef]
- Fang, J.C.; Ning, X.L. Installation Direction Analysis of Star Sensors by Hybrid Condition Number. IEEE Trans. Instrum. Meas. 2009, 58, 3576–3582. [Google Scholar] [CrossRef]
- Han, J.L.; Yang, X.B.; Yue, W.; Xu, T.T.; Wang, S.E.; Chang, L.; Yang, C.L. Image Motion of Remote Sensing Camera with Wide Field of View Over the Antarctic and Arctic. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3475–3484. [Google Scholar] [CrossRef]
- Xu, T.; Yang, X.; Wang, S.; Han, J.; Chang, L.; Yue, W. Imaging Velocity Fields Analysis of Space Camera for Dynamic Circular Scanning. IEEE Access 2020, 8, 191574–191585. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, X. Study on Enlarging the Searching Scope of Staring Area and Tracking Imaging of Dynamic Targets by Optical Satellites. IEEE Sens. J. 2021, 21, 5349–5358. [Google Scholar] [CrossRef]
- Li, D.; Xu, J.; Zhu, B.; He, H. A calibration method of DVL in integrated navigation system based on particle swarm optimization. Measurement 2022, 187, 110325. [Google Scholar] [CrossRef]
- Majumder, C.G.; Siva, M.S.; Kumar, A.; Philip, N.K.; Ieee. Control Algorithms for Improved High Pointing accuracy and Rate Stability in Agile Imaging Spacecrafts. In Proceedings of the 3rd Indian Control Conference (ICC), Indian Inst Technol Guwahati Campus, Guwahati, India, 4–6 January 2017; pp. 93–98. [Google Scholar]
- Li, Y.; Wei, X.; Li, J.; Wang, G. Imaging modeling and error analysis of the star sensor under rolling shutter exposure mode. Opt. Express 2021, 29, 15478–15496. [Google Scholar] [CrossRef] [PubMed]














| Parameter | Value |
|---|---|
| Focal length | 42 mm |
| Field of view | |
| Resolution | |
| Pixel length | 5.5 μm |
| Exposure time | 100 ms |
| Star magnitude limit | 5.2 Mv |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Yang, X.; Wu, M.; Yan, A.; Du, J.; Gao, S.; Tang, X. Analysis and Correction of the Rolling Shutter Effect for a Star Tracker Based on Particle Swarm Optimization. Remote Sens. 2022, 14, 5772. https://doi.org/10.3390/rs14225772
Fu Z, Yang X, Wu M, Yan A, Du J, Gao S, Tang X. Analysis and Correction of the Rolling Shutter Effect for a Star Tracker Based on Particle Swarm Optimization. Remote Sensing. 2022; 14(22):5772. https://doi.org/10.3390/rs14225772
Chicago/Turabian StyleFu, Zongqiang, Xiubin Yang, Mo Wu, Andong Yan, Jiamin Du, Suining Gao, and Xingyu Tang. 2022. "Analysis and Correction of the Rolling Shutter Effect for a Star Tracker Based on Particle Swarm Optimization" Remote Sensing 14, no. 22: 5772. https://doi.org/10.3390/rs14225772
APA StyleFu, Z., Yang, X., Wu, M., Yan, A., Du, J., Gao, S., & Tang, X. (2022). Analysis and Correction of the Rolling Shutter Effect for a Star Tracker Based on Particle Swarm Optimization. Remote Sensing, 14(22), 5772. https://doi.org/10.3390/rs14225772