Implementing Sentinel-2 Data and Machine Learning to Detect Plant Stress in Olive Groves

Abstract

Olives are an essential crop for Greece and constitute a major economic and agricultural factor. Diseases, pests, and environmental conditions are all factors that can deteriorate the health status of olive crops by causing plant stress. Researchers can utilize remote sensing to assist their actions in detecting these sources of stress and act accordingly. In this experiment, Sentinel-2 data were used to create vegetation indices for commercial olive fields in Halkidiki, Northern Greece. Twelve machine learning algorithms were tested to determine which type would be the most efficient to detect plant stress in olive trees. In parallel, a test was conducted by testing 26 thresholds to determine how setting different thresholds for stress incidence affects model performance and which threshold constitutes the best choice for more accurate classification. The results show that among all tested classification algorithms, the quadratic discriminant analysis provided the best performance of 0.99. The stress incidence threshold used in the current case to generate the best-performing model was 6%, but the results suggest that setting customized thresholds relevant to specific cases would provide optimal results. The best-performing model was used in a one-vs.-rest multiclass classification task to determine the source of the stress between four possible classes: “healthy”, “verticillium”, “spilocaea”, and “unidentified”. The multiclass model was more accurate in detection for the “healthy” class (0.99); the “verticillium” and “unidentified” classes were less accurate (0.76); and “spilocaea” had the lowest score (0.72). Findings from this research can be used by experts as a service to enhance their decision-making and support the application of efficient strategies in the field of precision crop protection.

1. Introduction

The olive (Olea europaea L.) is one of the most important crops in the Mediterranean Basin, representing 95% of global production. Olive-growing has been traditionally localized in the Mediterranean Basin for thousands of years. According to the International Olive Council (IOC, http://www.internationaloliveoil.org/, accessed on 21 June 2022), there is more than 11 million ha of olive trees in more than 47 countries. The majority of this surface (97.9%) is localized in the Mediterranean countries, with Greece being the third-largest producer after Spain and Italy. However, new intensive orchards have been planted in the Mediterranean and in new regions (e.g., Australia, North and South America) over the last 20 years. This expansion and intensification of olive growing, as along with the perception of olive oil and table olives as healthy foods, has greatly increased both the production and demand of these products [1].

According to Eurostat (2016) (https://ec.europa.eu/eurostat/databrowser/view/ef_lpc_olive/default/table?lang=en, accessed on 21 June 2022), olive trees are the most widely grown trees in Greece, covering an area of 700.000 ha. Almost 124.000 ha is occupied by agroforestry systems, where different crops or pasture are planted in the understory of olive trees [2]. All regions with a mild Mediterranean climate are home to olive trees, which can be found growing alone or in orchards [3]. In the conventional systems, almost all olive trees come from grafted wild species. The primary outputs of olive trees are edible olives and olive oil, while minor goods include firewood and animal feed. In Greece, olive cultivation has been combined with grazing animals such as sheep, cattle, goats, pigs, chickens, or even honeybees. Olive trees have also been co-cultivated with cereals such as wheat, corn, or alfalfa, with grape vines or vegetable crops such as potatoes, melons, and onions, or with beans and fava beans, and in many cases with wild herbaceous vegetation, some of which is edible [2]. All agricultural units face environmental adversities during their biological cycle in the form of pests, diseases, and climate conditions such as extreme temperature and precipitation. These adversities are often expressed as plant stress. Grace and Levitt [4] proposed that plants are subjected to many forms of environmental stress. Some stress sources are abiotic physicochemical stressors, such as drought, cold, heat, or high salinity, while others are biotic, such as herbivory, disease, and allelopathy. The authors noted that the common feature of stress is the formation of reactive oxygen species at the cellular and molecular levels, which are strong oxidants that can cause significant damage to membrane systems and plant DNA. Often, the term “plant stress” is used in a broad sense, and so it is useful to define better it as a concept. Lichtenthaler [5] recognized this need and provided insight into the matter by defining plant stress as “Any unfavorable condition or substance that affects or blocks a plant’s metabolism, growth, or development. Vegetation stress can be induced by various natural and anthropogenic stress factors”.

More specifically, plant diseases have constantly been a significant concern for horticulture, since they strongly and adversely affect the production and quality of products. The impacts of biotic crop stresses, such as diseases and pests, fluctuate from minor side effects to extreme losses of whole yields, which bring about major expenses for agricultural businesses and intensely affect the agricultural economy. Evasion of these significant disasters can be accomplished via various strategies focusing on timely identification of stress factors. It has to be said that it is difficult for growers to apply these strategies, as a significant number of them are inaccessible and regularly require explicit domain knowledge, and they are often costly and resource-intensive. The absence of reliable, dedicated, and far-reaching services restricts growers’ actions in being proactive in their efforts towards the containment of epidemics, as ground-level detection is hard to apply continuously and consistently. With respect to defining stress, it was deemed important to try to define the procedure that is followed when a classification model has to determine if and when the experimental target—for example, a plant or a field—is suffering from a stress factor (e.g., disease) or not. This was also researched by Zhang et al. [6], who evaluated the effectiveness of a disease incidence strategy in enhancing disease detection algorithms. More specifically, in their study, Zhang et al. investigated the effects on the sensitivity of disease detection algorithms when setting different thresholds for separate regions. Their results indicated that compared to applying the same algorithm and threshold to the whole region, setting an optimal threshold in each region according to the level of disease incidence (i.e., high, middle, and low) enhanced the sensitivity.

A way to frequently and efficiently monitor crop health in large areas is by using remote sensors such as satellites, airplanes, and UAVs. Satellites provide the widest possible coverage at the lowest relative cost, as they provide a multitude of data at various wavelengths beyond the visible, over large regions. Remote sensing also supports methodologies that can assess crop health via the utilized sensors—sometimes even more accurately than experts in the field. In recent years, Sentinel-2 data have gained the attention of the remote sensing community for cropland mapping due to their high spatial (10 m), temporal (5 days), and spectral (13 bands) resolution, free and open access, and availability for cloud computing (Google Earth Engine, GEE) [7]. For example, Sentinel-2-derived data have been successfully used to detect and discriminate between different coffee leaf rust infection levels caused by Hemileia vastatrix [8]. Sentinel-2 data and vegetation indices have also been used to quantify the severity of hail damage to crops [9]. In a brief review, Yang [10] provided an overview of remote sensing and precision agriculture technologies that have been used for the detection and management of crop diseases. The instruments discussed in the review were airborne or satellite-mounted multispectral sensors and variable-rate technology used for detecting and mapping fungal diseases. The authors of [11] compared the efficiency of fungicide applications based on different application strategies in terms of product, dose, and timing selection in cereal crops in Australia and New Zealand. In their work, they addressed the advantages, disadvantages, and efficiency of fungicide application based on plant development stage or disease threshold. The onset of disease in wheat crops, along with the disease threshold to determine fungicide sprayings, was deemed to be an important factor concerning the efficiency of fungicide spraying. In [12], disease incidence thresholds were used to determine whether chemical control would be applied to coffee plants. The threshold for disease incidence was calculated by dividing the number of leaves with coffee leaf rust symptoms (i.e., lesions) by the total number of leaves of each plant. This result was then multiplied by 100 to provide a % range. For their experiment, they selected a 5% disease incidence threshold for chemical control. The authors of [6] tested the effects of different alert thresholds on the performance of detection algorithms for disease outbreaks. It was found that selecting different, parameterized thresholds instead of fixed alert thresholds for each region and incidence category improved the aberration detection performance of the tested algorithms.

The usefulness of the utilization of optical sensors to accurately detect plant diseases was recognized by Kuska and Mahlein in their study [13], although they recognized that there are challenges to the practicality of applications in the field, and that the development of sophisticated data analysis methods is required.

The need to solve problems in applying such techniques for more effective plant disease protection is also recognized. In the research carried out by Yuan et al. [14], the capacity of satellite information to monitor pests and diseases was also shown. Worldview 2 and Landsat 8 data were used to compute vegetation indices and environmental features. Immitzer et al. [15] utilized preliminary Sentinel-2 data and a variety of analysis approaches to map vegetation in order to produce land cover maps. Part of their research used Sentinel-2 data to differentiate crop types and seven deciduous and coniferous tree species for forest management. Their results suggest that many of their analysis methods achieved high accuracy. In a study by Ruan et al. [16], Sentinel-2 reflectance data and vegetation indices were used to develop a multi-temporal wheat stripe rust prediction model. The model’s results suggest that early disease prevention is achievable. Dhau et al. [17] used 10 m Sentinel-2 data and vegetation indices in 2021 to successfully detect and map maize streak virus.

Vegetation indices are combinations of the surface reflectance of two or more wavelengths. They can be correlated with a specific property of vegetation and highlight it—a procedure that can simplify detection of the correlated property, i.e., damage levels in crops [18]. In a study by Isip et al. [19], vegetation indices derived from Sentinel-2 data were evaluated for their ability to detect twister disease—caused by the fungus Gibberella moniliformis—on onions. Hornero et al. [20] used Sentinel-2 data to calculate spectral indices able to provide spatiotemporal indications for tracing and mapping Xylella fastidiosa damage on olives. Navrozidis et al. [21] also used vegetation indices derived from Landsat 8, as a wide cover, and Pleiades-1A, as a very-high-resolution satellite, for Stemphylium purple spot detection purposes on asparagus plants. PlanetScope high-resolution satellite data were used to detect sudden death syndrome in soybeans [22]; in their analysis, the authors employed spectral bands, the normalized difference vegetation index (NDVI), and crop rotation data to build a random forest model.

Machine learning utilizes satellite data efficiently, supports big data analytics, and provides crop health assessment models. Using remote sensing data, machine learning classification algorithms such as SVM, ANNs, LDA, and RF can be utilized to detect plant diseases proactively. Binary, multiclass, multi-label, and hierarchical classification tasks are common in machine learning. Plant stress detection can be binary to discriminate between healthy and stressed plants or multiclass to identify disease classes [23]. In their study, Koklu and Ozkan [24] investigated the ability to differentiate between dry bean seed varieties using a computer vision system. Their aim included using images from a high-resolution camera and testing various machine learning classifiers in order to find the best-performing model. They achieved high performances in the testing of all classifiers, with SVM performing the best. Another multiclass study was carried out by Pirotti et al. [25], where nine machine learning algorithms were tested for accuracy and training speed in the classification of land cover classes, using Sentinel-2 data. Chakhar et al. [26] used data from Landsat 8 and Sentinel-2 and tested the robustness of 22 nonparametric classification algorithms for classifying irrigated crops.

Based on the presented literature for detecting biotic and abiotic plant stresses in olive fields, it can be noted that there is no available tool able to provide information on stress assessments for large areas at low cost and with sufficient accuracy. Additionally, because of the plethora of available approaches for machine learning classification models, their performance was investigated for tasks concerning plant stress detection. Finally, the methodology that is being proposed in this work can support the reduction in user/observer bias in classification tasks by encouraging customization of incidence thresholds for the labelling process, thereby highlighting the best-performing classification algorithms in machine learning tasks.

The aim of this work was to develop a methodology for detecting stress incidence in olive orchards utilizing Sentinel-2 data and machine learning. The specific objectives were (i) to identify the best-performing classifier, (ii) to select the optimal threshold for characterizing plant stress (disease incidence thresholds), and (ii) to identify the source of the stress.

2. Materials and Methods

2.1. Test Area

The prefecture of Halkidiki is located in Northern Greece (Figure 1) and is an active agricultural zone, with a large amount of the agricultural land used for olive cultivation. Varieties cultivated in Halkidiki include the region’s namesake “Halkidikis”, but also “Amfissis”, “Kalamon”, and other local varieties such as “Galano”, “Metagitsi”, and “Agioritiki” used to produce green and black olives or virgin olive oil. One of the most commonly used varieties of olive in the region is the “Halkidikis” variety, which produces a very high-quality final product but is also one of the varieties most heavily affected by biotic and abiotic stresses—and especially water stress.

The main crops in the area incorporate monocultures of cereals and olive orchards. There are also scattered agroforestry systems composed of olive trees intercropped with cereals and grasses, as cover crops, with the trees’ density ranging from 20 to 60 trees/ha [2]. The mean annual temperature of the area is 16.5 °C and the mean annual precipitation is 598 mm. In order to achieve high yields, the majority of growers irrigate their fields, mostly using private groundwater pumps, resulting in favorable growth conditions for soil-borne fungal pathogens, such as Verticillium dahliae, as well as airborne pathogens, such as Spilocaea oleaginea. The disease caused by V. dahliae is called Verticillium wilt, with symptoms that greatly resemble extreme water stress conditions in olive trees, and is claiming increasing numbers of fields each year. The most important part of the biological cycle of olive trees, with respect to their optimal development, is between April and June in Northern Greece. Sampling for this experiment took place during these months in the years 2019 and 2020. The disease caused by S. oleaginea is commonly known as peacock’s eye internationally, and locally as Cycloconium.

2.2. Sampling Procedure

In order to reach the set objectives, two types of data were necessary: ground-truth data from olive orchards, and Sentinel-2 data for the noted samples.

The samples collected for ground truthing and later used for this analysis were polygons inside the borders of olive orchards in Halkidiki (Figure 2).

The term polygons, referring to the samples, is used interchangeably with the term sampling units throughout this text, each representing a single sample. Each sample’s location was selected in representative parts of the orchard to which it belonged; based on the distances between each individual tree in the orchards, the mean was 18 olive trees in a sample, while based on the mean radius of trees’ vegetation there was a mean 195 m² of olive tree vegetation per sample. In total, 222 samples were collected.

Sampling units contain information associated with biotic- and abiotic-stress-related assessments carried out by visual inspection and laboratory analysis of samples with ongoing symptoms. That is, each sample, in addition to the polygon and its geographical information, also includes assessments that were recorded in the form of percentages of symptoms observed in the total olive tree vegetation surface present in each sampling unit. Accompanying the assessments is a list of factors that may affect reflectance data from the sampling units. These include ground cover vegetation, tree biomass, and irrigation of the crop, as well as the variety of the assessed trees. Vegetation present in the ground is always included in the reflectance value of each pixel and accounts for all reflectance corresponding to the sampling unit that is not attributed to tree foliage.

Symptom percentages were attributed to three possible classes:

• Verticillium dahliae;
• Spilocaea oleaginea;
• Unidentified stress factors.

The values recorded were used to characterize healthy trees and the percentages of V. dahliae, S. oleaginea, and unidentified stress factor (USF) symptoms in the samples. USFs were used to denote all other non-classified surveyed symptoms attributed to diseases, pests, or abiotic-stress-related damage.

2.3. Creation of Stress Incidence Thresholds

Symptom percentages were summed to compute the “total stress” present in each sampling unit, the distribution of which is presented in Figure 3. This “total stress” value can be used, at the agricultural expert’s discretion, to determine the minimum plant stress percentage necessary to characterize a sample as stressed or healthy, without specifically attributing the source of plant stress to one of the classes. This minimum value is referred to as the “stress incidence threshold” or “threshold” in this manuscript and is used to create binary labels for each sample of “stressed” (1) or “not stressed” (0). For example, when setting a hypothetical threshold at 10%, all samples with a “total stress” value of 10% and above would be labelled as “stressed”, while samples with a “total stress” value below 10% would be labelled “not stressed”, resulting in a 10% label set.

Figure 3 displays the stress intensity from 0 to 100% for the samples recorded during the years 2019 and 2020 for the period May–July. Each bar represents a 10% class range for stress incidence. Most samples were attributed to the 0–10% class, which comprised 32.4% of the dataset, followed by the classes 10–20% and 20–30%. The size of the rest of the classes steadily decreases down to the smallest class of 90–100%, which accounted for the lowest number of samples.

In the above context, it can be said that setting a stress incidence threshold to classify a sample is subjective. To provide a less expert-related and unbiased answer to the issue of stress detection, 26 stress incidence thresholds—ranging from 5% up to 30%—were tested. To perform this test, 26 separate labelled sets were generated: one for each threshold. The procedure of applying a random search, as explained below in Section 2.9 “Classification algorithms”, was applied to each labelled set to find the threshold that could provide the best-performing model.

Thresholds lower than 5% and higher than 30% were excluded from the optimal thresholds for model selection, as they do not provide insight into the matter of stress detection. This is because these thresholds provide oversensitive and imprecise models (thresholds lower than 5%) that rely on symptoms that are non-existent or on unspecific models (higher than 30%) that require such a strong presence of damage in the crop to be able to detect it that it is not practical to use remote sensing or there are no practices to be applied to remedy the tree. This test can help identify the best-performing classification model for detecting apparent stress in olive orchards for each tested threshold, and it can also be used to display the differences in model performance per threshold tested.

2.4. Assignment of Stress Source

The stress incidence threshold found to provide the best-performing model among all tested labelled sets was also used for the purpose of completing the objective of identifying the source of detected stress in each sample. This was achieved by creating a field containing labels (“verticillium”, “spilocaea”, or “unidentified”) for stressed samples depending on the highest contributing stress class recorded, or “healthy” for unstressed samples.

2.5. Geographical and Satellite Data

SW Maps—a mobile mapping and GIS app—was used to store the geographical information of the collected samples in shapefile format so that they could later be accessed and processed. (https://play.google.com/store/apps/details?id=np.com.softwel.swmaps&hl=en&gl=US, accessed on 13 August 2020).

Sentinel-2 data were utilized in this study in the form of ready-to-use, bottom-of-atmosphere products (Level 2A) of 4 bands, with a maximum spatial resolution of 10 m for blue, green, red, and near-infrared. The satellite images collected complement the sampling period that took place between May and July in the years 2019 and 2020 (29 May 2019, 8 June 2019, 3 July 2019, 3 May 2020, 13 May 2020, 12 July 2020 and 17 July 2020).

Sentinel-2 data were accessed by using Sentinel Hub’s Feature Info Service (FIS, now “Statistical API”). This service from Sentinel Hub (https://www.sentinel-hub.com/explore/eobrowser/, accessed on 3 August 2020) was used to perform elementary statistical computations on the data used for the test area. This step facilitated access to specific pixels, rather than entire images, thereby making data processing more effective.

The final dataset acquired and used for analysis was a .csv file containing the sample ID, coordinates, image dates, and reflectance values (of atmospherically corrected Sentinel-2 product L2A) of the four 10 m Sentinel-2 bands mentioned above, along with the mean values of the vegetation indices computed using FIS, via pixels inside or covering the sample’s perimeter.

2.6. Data Analysis Tools

Python 3 with Jupyter Lab was used for all analysis steps, as it provides a convenient interface for data exploration, visualization, and model building. As an open-source software platform, Project Jupyter aims to facilitate interactive data science and scientific computing across all programming languages. Microsoft’s Power BI was used to generate and enhance visualization of the results.

2.7. Index Computations

All disease symptoms are attributed to anatomical and physiological deteriorations which, as a result, have a reflectance that is different from the typical reflectance of a healthy plant. Additionally, these deteriorations are often correlated with fluctuations in the concentrations of chlorophyll and carotenoids in plant tissues. Chlorophyll and carotenoid concentrations can be more easily correlated in specific spectral regions such as green, red, red-edge, and near-infrared. For this reason, 10 vegetation indices were used. In the current experiment, vegetation indices were calculated by incorporating the relevant spectral regions from Sentinel-2′s data (

Table 1. List of created vegetation indices calculated and used as training features.

Vegetation Index		Index Formula	Reference
NDVI	Normalized difference vegetation index	(NIR − RED)/(NIR + RED)	[27]
RDVI	Renormalized difference vegetation index	(NIR − RED)/sqrt(NIR + RED)	[28]
GNDVI	Green normalized difference vegetation index	(NIR − GREEN)/(NIR + GREEN)	[29]
SAVI	Soil-adjusted vegetation index	(NIR − RED)/(NIR + RED + 0.5) × (1.0 + 0.5)	[30]
EVI	Enhanced vegetation index	2.5 × ((NIR − RED)/(NIR + (6 × RED) − (7.5 × BLUE) + 1))	[31]
TVI	Transformed vegetation index	sqrt(((NIR − RED)/(NIR + RED)) + 0.5)	[32]
ARI1	Anthocyanin reflectance index 1	(1/GREEN) − (1/NIR)	[33]
ARI2	Anthocyanin reflectance index 2	NIR × ((1/GREEN) − (1/NIR))	[34]
CRI1	Carotenoid reflectance index 1	(1/BLUE) − (1/GREEN)	[33]
CRI2	Carotenoid reflectance index 2	(1/BLUE) − (1/NIR)	[33]

).

2.8. Data Cleaning and Data Augmentation—Oversampling

To remove outliers from the collected dataset and improve model performance in general, the interquartile range (IQR) data cleaning method was applied as shown on Equation (1). IQR is a good statistic for summarizing a non-Gaussian distribution sample of data by calculating the difference between the 75th and the 25th percentiles of the data.

IQR was used to identify outliers in the initial generated dataset containing spectral data, vegetation indices, and all features documented during sampling. This was achieved by defining limits on the sample values, i.e., a factor k of the IQR below the 25th percentile (Equation (2)) and above the 75th percentile (Equation (3)). A common value for the factor k is 1.5. A factor k of 3 or more can be used to identify values that are extreme outliers or “far-outs” when described in the context of box-and-whisker plots, but this was not relevant for our analysis.

IQR = Q3 − Q1.

(1)

Lower bound = (Q1 − 1.5 × IQR),

(2)

Upper bound = (Q3 + 1.5 × IQR),

(3)

With the binary grouping of the samples into the categories “Healthy” and “Stressed”, it is unavoidable—depending on the stress incidence threshold selected—to have one of the two classes under-represented in the resulting dataset. This derived “imbalanced dataset” is a common occurrence in classification objectives. When machine learning techniques are used to train a model, the minority class is often ignored, and the resulting model has a poor performance in classifying it. In order to address this issue, the minority class samples were oversampled. This was achieved by using the synthetic minority oversampling technique (SMOTE) [35] to synthesize data. SMOTE utilizes a k-nearest neighbor algorithm to create plausible new synthetic examples from a class that were relatively close in feature space to existing examples. SMOTE data augmentation was applied to each labelled set in both classes (“stressed” and “healthy”) to reach a maximum number of 200, which was derived by applying different incidence thresholds (5–30%) in order to create comparable datasets for every threshold.

2.9. Classification Algorithms

To find the best-performing classification model, a series of models were trained and evaluated, mainly utilizing the Python libraries pandas and scikit-learn. Models were trained for all different classification algorithms, hyperparameters, and threshold levels, retaining 33% of the data as a validation set. The algorithms tested belong to eight major machine learning categories for classification, as seen below:

• Ensemble modelling:
  • Random forest;
  • Gradient boosting machines;
• Artificial neural Networks:
  • Multilayer perceptron;
• Kernel methods:
  • Support-vector machines;
• Decision trees:
  • Decision trees;
  • Adaptive boosting;
• Discriminant analysis:
  • Linear discriminant analysis;
  • Quadratic discriminant analysis;
• Regression analysis:
  • Logistic regression;
• Bayesian networks:
  • Naïve Bayes Gaussian;
  • Naïve Bayes multinomial;
• Instance-based methods:
  • k-Nearest neighbors.

To identify the optimal model, a “randomized search” (RandomizedSearchCV) multiclass classification method was used, applying 10-fold cross-validation. The randomized search implemented a search over the grid of parameters displayed in

Table 2. List of classification algorithms utilized in the randomized search, along with the related hyperparameters.

Classification Algorithm	Tested Parameters	Min–Max Ranges of Tested Parameters
SVM	Gamma	Scale, auto, 0.001–10.0
	C	0.001–100.0
	Kernel	Rbf, sigmoid, linear
Random forest	N_estimators	100–500
	Criterion	Gini, entropy
	Min_samples_split	2–8
Decision tree	Criterion	Gini, entropy
	Splitter	Best, random
	Min_samples_split	2–10
Ada_boost	N_estimators	20–150
	Learning rate	0.01–2.0
Gradient boosting	Learning rate	0.01–2.0
	N_estimators	20–150
	Criterion	Friedman_mse, mse
Logistic regression	C	0.001, 100.0
	Max_iter	50–500
Naive Bayes Gaussian	Var_smoothing	0.000000001–0.1
Naïve Bayes multinomial	Alpha	0.001–1000.
	Fit_prior	True, False
k-Nearest neighbors	N_neighbors	1–20
	P	1–5
	Weights	Uniform, distance
	Algorithm	Auto, ball_tree, kd_tree, brute
	N_jobs	(−2)–1
MLP	Hidden layer sizes	50–150
	Activation	Identity, logistic, tanh, relu
	Solver	Lbfgs, sgd, adam
	Alpha	0.001–0.1
	Learning rate	Constant, invscaling, adaptive
	Max_iter	400–1000
Linear discriminant	Solver	Lsqr, eigen
	Shrinkage	None, auto, 0.01–1
	Store covariance	True, false
Quadratic discriminant	Reg param	0.0–0.5
	Store covariance	True, False
	tol	0.001

, where each setting was sampled from a distribution over the associated parameter values. The highest number of iterations for the randomized search was 100, during which the method searched for a better-performing model. The algorithm stopped this search earlier if no better-performing models were found for a selected number of consecutive iterations.

The testing procedure used leads to identification of the best-performing model, with respect to hyperparameter tuning, for each tested classifier and each stress incidence threshold. The different classification algorithms, along with the accompanying hyperparameters that were trained and evaluated, can be seen in the following table (Table 2).

This testing procedure resulted in 312 models, of which the best-performing model for each of the 12 classifiers for each incidence threshold was selected based on the AUROC score. The evaluation metrics that were used—and are presented in the next section to provide information about the performance of the tested models across all classification algorithms and stress incidence thresholds—were confusion matrix, accuracy, precision, sensitivity (recall, or true positive rate), specificity, false positive rate, F1-score, and area under the ROC curve (AUROC).

Confusion matrices were used to define the individual metrics mentioned above to help interpret the quality of the model outputs. The overall accuracy is given by the proportion of correctly classified samples, which explains the ability of the trained model to classify healthy and stressed samples correctly. Precision, in our case, describes the percentage of “stressed” classifications that were assigned correctly. Sensitivity describes the percentage of correctly classified stressed samples; it showcases how sensitive the classifier is in detecting positive instances. This is also referred to as the true positive rate, or recall. Specificity describes the percentage of correctly classified healthy samples.

F1-score provides information by producing a single metric combining the precision and recall of a classifier by calculating their harmonic mean. While this is suitable for comparing performances between multiple classifiers, it is often used in cases with imbalanced datasets. In the current case, since the data were oversampled, priority was given to the AUROC metric to evaluate performance.

The receiver operating characteristic (ROC) curve is a graphical representation of the performance of a classifier over all possible thresholds, indicating the diagnostic ability of the model. In an AUROC graph, the false positive rate and true positive rate are plotted on the x- and y-axes, respectively. The area-under-the-curve values range from 0.5 to 1 for a totally inaccurate or an ideal model, respectively. To avoid confusion, the threshold related to the AUROC score refers to the internal classifier threshold that the algorithm uses to determine how to classify a sample, and this is not to be confused with the stress incidence thresholds mentioned in the rest of the manuscript. To assess the performance of every trained model and, most importantly, its ability to equally differentiate between healthy/negative (0) and stressed/positive (1) samples, the area under the receiver operating characteristic curve (ROC curve—AUROC) was the key performance metric computed to evaluate the overall model performance for identifying stress incidence in the test set.

3. Results and Discussion

3.1. Classification Model Performance Comparison

The average performance for each tested classification algorithm is displayed in Figure 4. Across all eight tested classifier categories, the average performance ranged from 0.52 to 0.75. The best average performance was achieved by the nearest neighbors category, with an AUROC value of 0.75, closely followed by the performance of ensemble modelling, with an AUROC of 0.74. The performance of nearest neighbors was 44% better than the worst-performing category, i.e., the Bayesian networks. When each classifier was examined separately, across 12 tested classifiers, the average performance ranged from 0.51 to 0.76. Gradient boosting and random forest provided the same highest average performance for all thresholds, with 0.76, followed by k-nearest neighbors with 0.75 and multilayer perceptron with 0.74. The performance of gradient boosting and random forest was 48% higher than the lowest average of the naive Bayes Gaussian algorithm, with a performance of 54%. Figure 4 also displays the average sensitivity and specificity for each classifier and threshold. For sensitivity, at 0.67, random forest had the highest average, while the least sensitive was naive Bayes Gaussian at 0.43. Specificity had the highest average when using the adaptive boosting algorithm, with 0.73, and the lowest average with logistic regression, at 0.41. The greatest divergence between sensitivity and specificity occurred for the logistic regression algorithm, with a difference of 0.23, which suggests it was the best algorithm for detecting stressed samples but the worst for detecting healthy samples.

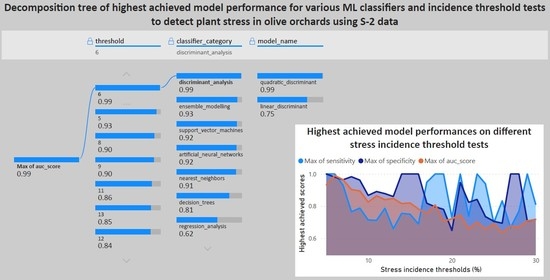
The best performance for the tested classification algorithms, along with the highest sensitivity and specificity, is presented for the various tests of the hyperparameters and thresholds examined (Figure 5). Across all 12 models, sensitivity ranged from 0.67 to 1, while specificity ranged from 0.74 to 1. The logistic regression, naïve Bayes multinomial, and quadratic discriminant analysis managed to produce models with 0.99 sensitivity and specificity. Naïve Bayes Gaussian had the biggest divergence between the two metrics, with a difference of 0.21 for the highest achieved scores.

The objective of the testing carried out in this approach was to assess and present the ability of Sentinel-2-derived data and vegetation indices to create a classification model for plant stress detection on olive orchards. The tests included classification algorithms belonging to categories widely used in classification problems such as ensemble modelling, nearest neighbors, neural networks, support-vector machines, Bayesian networks, etc. In the presentation of the results, the performances of both the broader classification categories and the individual classification algorithms are displayed along with their sensitivity, specificity, and performance on different thresholds. The results suggest that stress can be detected in olive orchards, but the classification algorithm that provides the best results varies depending on what is the main interest of the user. For example, the second-best-performing classifier was SVM, but it had worse results than other classifiers concerning specificity, and an even lower sensitivity. On the other hand, quadratic discriminant analysis provided the best-performing model, while also retaining sensitivity and specificity, as shown in Figure 5.

In the results, it is generally observed that when comparing classifiers and their categories in terms of the average performance achieved across all thresholds, the best-performing models are found by using different classifiers, depending on which statistical metric is important for the researcher or which incidence threshold is the most appropriate in each case. An overall suggestion concerning the selection of a “best” model would be to take into consideration which aspect of stress detection is the most important for the user—i.e., quality of predictions for stressed samples or overall quality of predictions—and select the model accordingly.

3.2. Evaluation of Stress Incidence Thresholds

To determine which stress incidence threshold provides the most efficient classifier and assess the effects of different incidence thresholds on classification performance, thresholds ranging from 5% to 30% were investigated. The heatmap in Figure 6 displays the best-performing model of each category for each threshold using the AUROC as the performance metric.

This heatmap supports a more thorough examination of the classifier category performance for each individual threshold, instead of their mean performance, and helps to pinpoint the best and worst performance achieved. The y-axis represents the categories of the classification algorithms tested, while the x-axis represents the thresholds to determine the incidence or absence of stress. Each value inside a cell represents the highest AUROC score of the hyperparameter combination used to achieve it for the respective classification algorithm and incidence threshold. The heatmap suggests that setting a low incidence threshold provides better-performing models in all classification algorithms. Some categories, such as Bayesian networks and regression analysis, do not perform well at any threshold, having achieved their best AUROC scores around 0.5–0.6, meaning that they categorize classes close to randomly, which would be an AUROC score of 0.5. For the remaining models, the best scores are achieved on the lowest thresholds (5–10%) and are above 0.85, after which they start dropping as the thresholds move towards 30%. Discriminant analysis algorithms are the most efficient based on the performance across all tested thresholds, but they also provided the best-performing models, with AUROCs of 1 and 0.99. This suggests that it becomes easier for any tested model to detect stress when we set a lower threshold rather than a higher one, meaning that stress can be better detected when trying to assess early symptoms of crop damage before it spreads.

Figure 7 displays the average performance (AUROC), sensitivity, and specificity for each threshold computed from all classifiers. Looking at the average performance for each threshold, the lower-end thresholds seem to provide better average performance, showing a slight decline as they go higher. Across all 26 tested thresholds, AUROC ranged from 0.57 at threshold 26 to 0.82 at threshold 5; in contrast, sensitivity ranged from 0.49 at threshold 27 to 0.79 for threshold 5. Specificity ranged from 0.47 at threshold 29 to 0.83 for threshold 8. AUROC had the fewest fluctuations between the three presented metrics across all thresholds, and it can be observed that in the majority of the thresholds, specificity was higher than sensitivity, which means that in most thresholds the models produced were, on average, better at detecting healthy orchards than stressed ones.

Figure 8 shows the best performance (AUROC) and the highest sensitivity and specificity achieved between all tested classifiers for each threshold. Examining the highest performance achieved for each threshold among all tested classifiers, the lower-end thresholds provide the best-performing algorithms, albeit declining in performance as the thresholds are set higher. Across all 26 tested incidence thresholds, the best sensitivity ranged from 0.66 to 1, the best specificity ranged from 0.65 to 1, and the highest AUROC ranged from 0.64 to 1. The best model performance was indicated at thresholds 5 and 6 for all metrics, thresholds 18, 19, 21, 23, and 29 for sensitivity, and thresholds 14, 15, 16, 27, and 28 for specificity. Relative to the average performance observed previously, although higher, most of the models had higher scores for specificity.

It can be deducted from the threshold performance plots that setting a higher threshold and, thus, accepting larger vegetation surfaces with various symptoms on an orchard, provides worse-performing algorithms. This observation suggests that all models are more accurate when trying to detect the incidence of stress at early stages, where the agronomist or producer is not willing to accept high presence of symptoms on the orchard to characterize the status as normal, healthy, or unstressed. Alternatively, it is more difficult for the models to distinguish between healthy and stressed orchards when the overall symptoms are present in higher amounts or are more spread-out.

To determine whether setting different stress incidence thresholds affects the detection performance of classification algorithms, a test was carried out where 26 labelled columns were created, scaling from thresholds of 5 to 30—increasing in increments of 1. Based on this, each sample was allocated values of 0 for “not stressed” or 1 for “stressed”, depending on the sample’s total stress value being lower or equal-or-greater than the threshold, respectively, and decided by individual total accumulated stress, as measured by symptoms per vegetation surface in the sample.

The results showed that setting different thresholds affects the average performance, sensitivity, and specificity of all models, showing a pattern of higher scores on lower thresholds (5–8) and deteriorating as the thresholds increased, until threshold 23 where the scores presented a slight increase up to threshold 30. A similar pattern can be observed in the maximum achieved performance where, although the highest scores are highlighted for each threshold, the highest performance is again evident in the lowest thresholds (5–9), followed by a constant decrease until threshold 26, where the performance starts increasing until threshold 30. Contrary to the presented pattern for the highest achieved performances, the highest achieved sensitivity and specificity for the thresholds can found at thresholds 5 to 6, but high scores appear again at thresholds 14 to 29 for sensitivity and specificity, suggesting that the most efficient threshold to use on each occasion would be best selected by incorporating the user’s domain knowledge and the case’s specific attributes. Comparatively, Zhang et al. [6] also tested the effects of setting different alert thresholds on the performance of disease detection algorithms. The alert thresholds for disease outbreaks were individually adjusted in various regions in accordance with the incidence of disease there to test how different levels of disease incidence affected the effectiveness of epidemic detection methods. The comparison took place between opting to apply the same algorithm and threshold to the whole region vs. setting an optimal threshold for each region according to the levels of disease incidence. In their results, it was demonstrated that adopting customizable surveillance alert thresholds by incidence category could improve the performance of the selected algorithms for disease detection. This insight was also evident in the current case, as the fluctuation in model performance, sensitivity, and specificity could be observed with different thresholds and classifiers. This suggests that selecting specific incidence thresholds could be more relevant for different cases of apparent stress in olive orchards.

Based on the evaluation of all applied tests for classifiers and thresholds, as described in the previous Section, the classifier that provided the best-performing classification model for stress detection was the quadratic discriminant algorithm, with 0.99 AUROC when setting the threshold for stress incidence at 6%. The AUROC plot for the indicated model can be seen below (Figure 9).

The accompanying hyperparameters that were used to produce this quadratic discriminant analysis model were as follows: covariance storing was set to true in order to explicitly compute and store class covariance matrices, and the regularization parameter—which was used to regularize the per-class covariance—was set to 0.0. For further practical comprehension of the model outputs, and based on the description for each metric, the explanation of the model’s performance metrics regarding stress detection is presented in

Table 3. Performance metrics for the quadratic discriminant analysis model at a stress incidence threshold of 6.

Performance Metric	Value
Overall accuracy	0.98
Average precision	0.97
F1 score	0.98
Sensitivity (recall, or true positive rate)	1.00
Specificity	0.96
False positive rate	0.04
AUROC	0.99

. Based on accuracy, the model was 85.8% accurate in its predictions for overall stress; it was 97% correct when detecting stressed vegetation and 96% correct when detecting healthy vegetation. When a sample was stressed, the model was able to detect it 100% of the time. In comparison, when the sample was healthy, the model—based on the false positive rate—was wrong at a 4% rate.

With respect to the applicability of the classifications, it should be noted that this classification does not provide any information about any specific stress sources. Moreover, it is not indicative of the stress intensity present in the sample, providing only the information that it has more than 6% stress. However, by providing information about the best-performing classifier category for the incidence thresholds tested, an opportunity is provided for the user to decide which threshold for stress incidence is more practical or relevant for a specific case and which classifier is most appropriate for detection.

3.3. Plant Stress Source Classification

By testing for the stress incidence threshold and the classification algorithm that provided the best-performing model, a threshold of 6% and the quadratic discriminant analysis algorithm were pinpointed as the optimal combination to detect plant stress. This optimal threshold (6%) was used to determine the stress incidence for each sample. After the labelling of a sample, an additional stress source label was added to the sample, belonging to four possible categories of stress: “healthy” (i.e., no stress), “spilocaea”, “verticillium”, or “unidentified”. This label was chosen depending on the stress factor that contributed most to the sample. The practical outputs of this Sentinel-2-based classification model are (1) to determine whether a field has a lot of ongoing symptoms or damage and should subsequently be considered stressed, and (2) to provide additional information as to what is the main source of the stress.

An overview of the dataset and how the samples are distributed in binary classes is presented in Figure 10a. Additionally, the density of labelled samples attributed to the four different “Stress source” classes—namely, “healthy”, “spilocaea”, “verticillium”, and “unidentified”—is shown in Figure 10b.

The one-vs.-rest (OvR) multiclass classification method used in this case compares the probability of a prediction belonging to a specific class against the probability of it belonging to any other class, and this procedure is repeated for each class. One class (one) is considered the “positive” class, while all other classes (the rest) are considered the “negative” class. By following this categorization procedure, the multiclass classification is essentially divided into a number of binary classifications—one for each class. The outputs of the model provide an AUROC for each class, as shown in Figure 11, along with a histogram of the probabilities of the classifier predicting the target class vs. all other classes.

The top row of Figure 11 presents bar graphs of the probability of the samples for each binary comparison belonging to the “Rest” category or the target category, by classifying them using 0.5 as the probability threshold, while the bottom row presents an accompanying AUROC curve for each bar graph. Observing the pairs of bar and AUROC graphs, “healthy–Rest ” is the comparison providing the most correct classifications between the classes, while “spilocaea–Rest” displays the most mixing between the two categories and produces the worst-performing binary classification among the four, as is also apparent from the slope of the accompanying AUROC graph. As shown in the confusion matrix (Figure 12) and

Table 4. Performance metrics for the one-vs.-rest multiclass classification model.

	AUROC	Precision	Sensitivity	F1-Score	Support
Spilocaea oleaginea	0.72	0.60	0.56	0.58	27
Healthy	0.99	1.00	0.75	0.86	20
Unidentified	0.76	0.47	0.45	0.46	20
Verticillium dahliae	0.76	0.44	0.63	0.52	19
Mean AUROC	0.81
Accuracy				0.59	86
Macro average		0.63	0.60	0.60	86
Weighted average		0.63	0.59	0.60	86

, the model has a mean AUROC score of 0.81. According to the depictions on the ROC charts shown in Figure 11, the healthy classification performance is the highest, with an AUROC score of 0.99, followed by the “verticillium” and “unidentified” detection performances with a score of 0.76 each. There is a slight drop in performance for “spilocaea” detections, at 0.72 AUROC.

Based on the rest of the presented scores in Table 4, which mostly follow the pattern displayed by the performance for each class, it can be seen that the precision for the “healthy” class is 1.00, meaning that when the model predicts that a sample is “healthy” it is always correct. If we observe the sensitivity for the “healthy” class, when a sample is actually healthy, the model predicts it correctly 75% of the time, which is still the most accurate classification among all classes, but significantly lower compared to precision. The “verticillium” class provides the highest difference between precision and sensitivity, with values of 0.44 and 0.63, respectively. The precision for “verticillium” predictions is the lowest of the four classes, with a rate of 44% in identifying V. dahliae infections, so it is more probable that the prediction belongs to one of the other classes instead of the predicted class. In contrast, when a sample is infected with V. dahliae, this model has the second-highest probability to identify it correctly, with a 63% rate. The “spilocaea” class has the lowest AUROC of all of the classes but has the lowest differences between its performance metrics; a 0.60 precision means that when predicting the “spilocaea” class, the model is correct 60% of the time. In the same pattern, having a sensitivity of 0.56 is translated as a 56% efficiency in detecting the presence of stress in a sample with stress symptoms attributed to S. oleaginea. The “unidentified” class has similarly low precision to that of the “verticillium” class (0.47), so the model is correct 47% of the time when predicting “unidentified”, but also has a similarly low sensitivity (0.45), being capable of correctly predicting a sample stressed by unidentified sources at a 45% rate, which constitutes the worst performance among all classes.

When a sample is stressed, the model appears to confuse the correct class with other categories of stress, but not with healthy samples, following the high sensitivity and precision of the best binary model produced. This becomes more evident if we specifically observe the predictions for the “unidentified” class in the confusion matrix, where more samples are categorized as “verticillium” and “spilocaea” than the actual “unidentified”. On the other hand, when a sample is healthy, the model misses a low number of samples, but the misclassification is more uniform. Overall, based on macro-averaged precision (63%) and recall (60%) scores, it is evident that the model is not as efficient in terms of its ability to identify the correct source of stress on a sample.

The outcomes of this research can contribute to precision plant protection measures applied in olive fields. Regular stress assessments, as facilitated by using the developed models for each new Sentinel-2 image made available, provide a guide for agronomists monitoring the area of interest. They can use the presented methodology to choose an appropriate disease incidence threshold for a field or agricultural area and be alerted to areas where olive vegetation stress is occurring. In this way, any strategic plant protection actions can be coordinated at the proper time, while also avoiding actual transfer to each individual field and, therefore, reducing transport costs.

Moreover, by exercising the option to set a low threshold, an expert can be informed of emerging damage in an otherwise healthy field. Additionally, the ability to monitor a specific field or region using a stress incidence threshold of the user’s choice allows for fewer unwanted alerts, since a selected threshold is more representative of the field’s vegetation state.

4. Conclusions

In this study, a methodology is presented for detecting and classifying plant stress in olive orchards using Sentinel-2 spectral data and machine learning. After preprocessing the dataset, it was considered important to apply an oversampling technique on the labelled data, so as to be able to diminish the effects of class imbalance—especially because of the method changing the stress threshold, which produced differently sized data.

After testing to find the best-performing algorithm among those tested, quadratic discriminant analysis was found to be the classifier with the best performance among all tested classification algorithms (0.99); SVM (0.93), random forest (0.93), and multilayer perceptron (0.93) also provided high performances. On evaluating the effects of setting different stress incidence thresholds, it was demonstrated that different incidence thresholds can provide more sensitive or specific models, and that user choice based on background domain knowledge plays an important role in generating efficient models. To a great degree, setting lower thresholds provided an overall better performance based on the majority of the tested classifiers. When using quadratic discriminant analysis—the best-performing classifier discovered—for a stress threshold of 6% to classify different sources of stress, the classification results were of lower accuracy compared to the binary classification, but they provided sufficient suggestions for healthy trees or trees with more apparent Verticillium-induced stress. The procedure for the multiclass classification follows the one-vs.-rest methodology, where each class is predicted against the remaining classes, and the label is decided based on the highest probability. The most accurate class to be predicted by the model was “healthy”. Samples with ongoing stress from unidentified sources were also mixed up with V. dahliae and S. oleaginea classes by the model, but not with healthy samples. The models produced could be further improved by the hybrid use of machine learning methods, deep learning, and new algorithms.

Based on these results, it can be concluded that Sentinel-2 satellite images do not provide sufficient information for pathogen identification. Instead, Sentinel-2 data can be used as a large-scale monitoring and alert system for olive orchards in Greece, assisting crop protection experts in forming adapted, site-specific solutions. Machine-learning-based supervised classifiers were proven to be able to provide the necessary tools to create highly accurate models appropriate for a wide array of user-determined thresholds.