A Novel Scheme about Skeleton Optimization Designed for ISTTWN Algorithm

Abstract

The ISTTWN algorithm overcame the defect of separating the production process of skeleton points and skeleton lines in tree branch point cloud skeleton extraction and improved the accuracy of the extracted initial skeletons, but the skeletons need further optimization. In the existing skeleton optimization, it is difficult to see the stump adjustment, and most of the bifurcation optimization and skeleton smoothness adopt fitting. Based on the characteristics of the initial skeletons extracted by the ISTTWN algorithm, this research optimizes the skeleton from four aspects. An algorithm for the stump adjustment for reconstructing the stump based on the layer and hierarchical relationship and an algorithm for the bifurcation optimization based on the local branch point cloud and cosine correlation are proposed, and an existing pruning method and a skeleton smoothing method are used. The results show that the skeleton optimization method proposed or used in this research has a high computational efficiency in general and can ultimately retain the necessary skeleton lines. In a visual analysis, the optimized skeleton is obviously much more natural and more in line with the actual topology of trees. In the quantitative analysis, the completeness, accuracy and effectiveness reached 97.82%, 95.72% and 89.47%, respectively. In this study, in addition to the existing tree parameters extracted by the skeleton or generalized cylinder model, the generated skeleton is used to extract the branch attributes. The $R^2$ of the deflection angle of the branch tip, distance from branch tip and branch length are about 0.897, 0.986 and 0.988, respectively, which illustrates that their models are very good. This research can further expand the application of the skeleton.

1. Introduction

As the shapes of different trees in nature are various, making and visualizing 3D tree models in the field of Computer Graphics is always a hot research topic and has been developed for at least half a century. This research has been similarly affecting forestry in recent years, attempting to find the possibility to replace the method of traditional forest investigation [1]. The way of combining an advanced surveying and mapping technique with novel information technology has gradually been widely used and is steadily developed to improve the visual effect and the reality of 3D tree models. In addition, in forestry, it can also be used to obtain more accurate existing parameters from measured single trees or the whole measured standing forest without a manual measurement, and some novel and meaningful parameters can be further proposed to describe the form not at the scene, know the actual situation and help make forecasts and plans [2,3].

LiDAR technology has been developed for one decade, and it uses lots of spatial points (these constitute the point cloud) to approximately describe the surface of objects in the measuring zone. If a LiDAR scanner is used to scan a tree and irrelevant parts in the tree point cloud are filtered out, a tree point cloud model, one type of tree model, will be presented. Some parameters that only rely on point information, such as tree heights, the DBH, the crown width and the clear bole height (CBH), can be obtained directly or indirectly by this kind of tree model [4]. Apart from that, many parameters cannot be obtained, such as branch length, branching angle and tree volume [5]. This is because this type of tree model is unorganized and has noise. In addition, it also has a disadvantage of huge storage. Therefore, it usually plays a role in the input or source data of other types of tree models. The generalized cylinder model is one of the commonly used types and it uses cylinders or truncated cones to fit the tree branch point cloud. The axes of these cylinders or truncated cones correspond to the lines on the tree skeleton. It can be asserted that the visual effect of one tree model and the accuracy of the subsequent extraction of the parameters highly depend on the effect of the skeleton extraction. After a branch model is produced, the models of the leaves will be virtually added by a certain algorithm [6]. With the model of trees, many studies not only extracting tree parameters can be carried out. For example, Huang et al. [7] tried to retrieve aerodynamic parameters in rubber tree forests by modeling trees with TLS point clouds.

The existing algorithms for extracting the skeleton from a tree branch point cloud can be divided into three major categories—algorithms based on Voxel Space, algorithms based on Point Clouds Contraction and algorithms based on a Geometrical Characteristic (hereinafter referred to as the VS, PCC and GC algorithms, respectively). Shi [8] pointed out that, in general, GC algorithms are next to PCC algorithms in computational efficiency but are the best or equally excellent among the three in dealing with small offshoots, the model topology and overall effects, as well as dealing with adjacent bifurcations and central deviation. In addition, he concluded that GC algorithms have the relatively best performance among them. In fact, there is still a frequently used algorithm named the Space Colonization Algorithm (SCA) [9] that does not belong to any of the categories. However, as it is hard to control the type of trunk bifurcations [10], the SCA is mainly used to simulate the small offshoots [11] through the leaf point cloud. Alternatively, it can be applied to extracting the tree skeleton with sparse points on the part of the branch from the tree point clouds obtained by ALS scanning [12]. As the Unmanned Aerial Vehicle (UAV) technique has been widely used with its low cost, high resolution and portability [13], there will be more research using ALS point clouds to extract tree skeletons and model trees [14]. Apart from the SCA, in general, the TLS point clouds are the data source of the mentioned algorithms for a skeleton extraction.

The reason why GC algorithms can be better in keeping the original appearance of trees is that the common principle of the GC algorithms is to cluster the branch point cloud by utilizing the similarity of the local features. According to the chosen feature or features, different GC algorithms can be divided into three categories—layering by the similarity of the shortest-path distance from each point to the root point (or layering by the shortest-path distances), such as Xu et al.’s [15]; layering by heights, such as Gao et al.’s [16]; and layering by spatial orientation and the radius of the branch (or layering by the tree branching geometry), such as You’s [17] and the TreeQSM [18]. It should be noticed that algorithms that adopt layering by tree branching geometry integrate one of the other two categories (where the height’s rising direction is not necessarily along the positive direction of the z-axis) and introduce extra information obtained from the tree branch point cloud to distinguish the points, which brings complexity for programming.

The initial outputs, produced by any algorithms for extracting tree skeletons from branch point clouds, exist inaccurately in many detailed positions and have a poor local visual effect. So, the procedure of skeleton optimization (or skeleton refinement) is imperative. It contains many aspects.

One, the breakpoint connection. Breakpoints make the skeleton unconnected, and the reconstructed tree model will form multiple parts. Xu et al. [15] used the existing trend of the skeleton and angle constraint to ensure the connection between the breakpoint and the main skeleton. Shi [8] pointed out that the Arterial Snake Model (ASM) proposed by Li et al. [19] can be used to deal with breakpoints by the fitting, growth merger of the arterial snakes. Zhou [20] proposed that a Cardinal Spline can be used to interpolate the vacancy caused by a breakpoint. Sun et al. [21] proposed an algorithm for using the change in adjacent angles formed by skeleton lines near the breakpoints to decide which skeleton points should connect to the breakpoint. Zhang et al. [22] defined a part of a regularizer for penalizing the positions of skeleton points in the different blocks belonging to the two joints, which is used to fix the breakpoints.

Two, the bifurcation optimization. In the initial skeleton, the lines at the bifurcations are always sharp and do not go through the center of the local point cloud. He et al. [23] pointed out that a bifurcation node, its parent node, its child nodes on all sub-branches and the tangent vectors formed by these nodes can construct a Hermite curve to fit and interpolate some transition points. Linvy et al. [24] used a Branch-Structure Graph (BSG) to differentiate different branches and the constructed local generalized cylinder models to compute an overlap rate between two cylinders in order to recognize which edge should be removed. He [25] proposed that after a reliable point found by the RANdom SAmple Consensus (RANSAC) is identified, its subsequent 16 points can use parabola fitting to estimate the suitable bifurcation point. Wang [26] adopted a rule to find a suitable connection where the angle between a parent branch and a sub-branch is no more than 45 degrees. Nouri et al. [27] reused and modified the idea of GC algorithms layering by axial heights to reconstruct local skeletons at bifurcations. Xu et al. [28] gave an algorithm for modifying the local skeleton at a bifurcation on the basis of the direction-first principle and combined with the idea of the shortest path. Fu et al. [29] adopted a way of refinement that, firstly, executed K-Means Clustering with several chosen initial cluster centers at a bifurcation, and the corresponding local point set as inputs and clusters can be obtained; then, similar to the approximation method, the local skeleton points and lines can be reconstructed by repeatedly excluding recognizable points on branches from a cluster and recomputing the centroid of the rest points by Cylindrical Prior Constraint (CPC) optimization.

Three, the skeleton smoothness. The initial skeleton lines in the part of each branch are unnatural and have excessive changes in their direction. Mei et al. [30] applied a Laplacian-based contraction which belongs to the PCC algorithms into the skeleton smoothness by modifying the parameter of controlling the force of a contraction in the matrix equation in order to enable it to adjust the smoothness. Li et al. [31] provided a simple method of directly averaging a continuous three points into the new middle one. Chaundhury et al. [32] pointed out that a B-spline curve can be used to resample each branch part of the tree skeleton, and they proposed Stochastic Modeling—a modeling technology for controlling the termination of skeleton smoothness according to the Degree Of Difference (DOD) between each part of the tree point cloud and the corresponding skeleton. Xu et al. [33] used a method by introducing 3D coordination differences which are used instead of directly averaging three points and a coefficient to balance the smoothness result, and after several rounds of iteration, the skeleton can be obviously more natural in the visual.

In addition, the pruning twigs, filtering isolated skeleton points and merging too close points are also frequently used according to the requirement of a study [34]. According to the feature of an algorithm, the skeleton optimization scheme can be selected from above, or additional methods can be designed. For example, Li et al. [35] designed an overall translation for the skeletons produced by a similar implement as AdTree.

We proposed an algorithm to extract the branch skeleton from the tree point cloud in the way of an Incomplete Simulation of Tree Transporting Water and Nutrients, which was named as the ISTTWN algorithm in short—a new GC algorithm layering by the shortest-path distances to simulate the transporting process of water and nutrients in a tree [36]. Compared to the previous various algorithms for extracting the tree skeleton from the branch point cloud, this method overcomes the defect that the process of producing skeleton points is out of sync with the process of connecting skeleton lines. In addition, when producing a new skeleton point and forming the skeleton line related to it at the same time, the result showed that the produced initial skeletons have a more accurate topology and cost a relatively short time. In this research, we will give some methods of skeleton optimization suitable for the ISTTWN algorithm. All the methods follow the common principles that any skeleton points obtained by fitting, which does not rely on point cloud information, will not be produced, and that the existing stable skeleton points cloud will not be removed. Based on this principle, our contributions in this research are as follows:

(1)

We proposed a new aspect of skeleton optimization, which was named as the stump adjustment, and designed an algorithm for reconstructing the stump based on the layer and hierarchical relationship.

(2)

We proposed an algorithm for bifurcation optimization based on the local branch point cloud and cosine correlation.

(3)

After additionally adopting pruning twigs and Xu et al.’s [33] skeleton smoothness, we verified the differences between unoptimized skeletons and optimized skeletons and tested the optimized skeletons to extract some branch attributes and evaluate the accuracy.

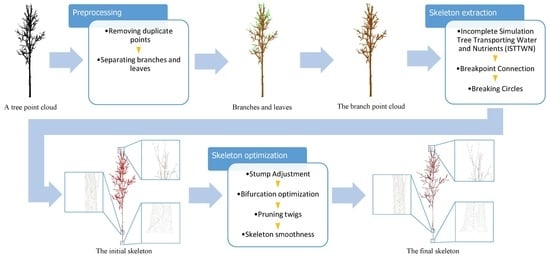
2. Materials and Methods

Figure 1 is the flow chart about all the steps to obtain an optimized skeleton from a tree branch point cloud.

2.1. Source and Preprocessing of Experimental Data

2.1.1. Data Source

We used three tree point clouds. Two of them were randomly chosen from the public tree point cloud dataset provided by Seidel et al.’s [37] research, including a European Ash (Fraxinus excelsior) and a European Oak (Quercus robur L.). In addition, the remaining one was randomly chosen from the preprocessed point clouds of sample plots of American black poplar (Populus deltoides) scanned by RIEGL VZ-400i Terrestrial LiDAR Scanner (TLS) with scanning mode Panorama40. The three tree point clouds are shown in Figure 2. All point clouds executed the removal of duplicate points.

2.1.2. Separating Leaves and Branches

According to optical properties of LiDAR and considering that TLS is usually placed on a tripod on the ground, the point cloud of a tall tree scanned by TLS has high resolution at the trunk and low resolution on the crown. This makes it difficult to form points at petioles. Therefore, the parts of leaves can relatively be clearly differentiated with the parts of branches. We adopted a method similar to region growing by choosing an initial point at the trunk, adding it into the set that represents branches and continuing to expand the set with all unadded neighbor points of each point in it until there are no more points added in. At this time, points still not added into the set are all thought of as points on leaves. This method is implemented by a kd-tree and its radius search to complete separation [38], where radius parameter $r=10\rho$ ($\rho$ is the average resolution) and there must be no duplicate points in the input tree point cloud. This method is suitable for any kind of tree point clouds as it only uses spatial coordinate information. Certainly, in order to improve accuracy, it is suggested that trees should be best scanned in leafless seasons. Figure 3 shows three tree point clouds’ results of separating leaves and branches. In this research, we only used the branch point clouds.

2.1.3. Computing the Shortest-Path Distances

Graph theory algorithms can be used to deal with point cloud when points in a point cloud are regarded as vertices and lines between each point and its neighbor points within a fixed certain range are regarded as edges and the length of each line is regarded as the edge weight. As points in the branch point cloud are all on branches, such a range should be chosen appropriately to ensure the graph is connected. In this research, we firstly computed an initial search radius calculated by equation

$${\rho }_{max}=\underset{\mathit{p}\in P}{max}\underset{\mathit{q}\in P-\left\{\mathit{p}\right\}}{min}{∥\mathit{p}-\mathit{q}∥}_2,$$

(1)

where $\mathit{p}$ and $\mathit{q}$ represent certain spatial points, ${\rho }_{max}$ is the maximum of all spacing between the points and their 1-nearest neighbor points in a point cloud. Such initial search radius is taken as cluster tolerance to cluster the branch point cloud (in the form of set) P using Euclidean Cluster Extraction (ECE). Then, we constructed a new undirected complete graph G with cluster indices as vertices, minimum cluster spacing between any two clusters as edge weights and computed Minimum Spanning Tree (MST) T of graph G. Finally, we set such range as the longest edge weight in T. This method can save memory for storing huge amounts of edge information to the maximum extent.

If such a graph could be regarded as an undirected connected graph, we set the shortest-path distance between a source vertex and all other vertices would be easily obtained by using algorithms solving the Single-Source Shortest Path (SSSP) problem. Point corresponding to the source vertex is chosen as the lowest one at the stump. The algorithm we used was the queue optimized Bellman–Ford algorithm.

2.2. Skeleton Extraction

The principle of ISTTWN algorithm can be described as a process that by using the shortest-path distances and the specified distance that water and nutrients are transported each turn (or step length), one part of points to produce skeleton points and the rest points to continue transporting can be decided. In addition, a clustering algorithm (here, use ECE with $eps={\rho }_{max},MinPts=1$) can help distinguish whether there are different offshoots or not, then the produced skeleton points can connect with the skeleton point in the same offshoot in previous turn.

It is obvious that the algorithm is recursive. As recursion is very slow, we tried some methods to improve it, including using iterative acceleration by interval segmentation and using multithreading. These improvements indeed decrease the cost of time and memory usage. However, the cluster object in improved ISTTWN algorithm is different from that in original ISTTWN algorithm, as the former is all the unexplored points in the whole branch point cloud, while the latter is just those in a local part. For improved ISTTWN algorithm, on the positive side, this difference can solve the issue that two too close branches are erroneously interpreted into one branch in a certain range. The range is a sphere which radius is equal to the product of step length multiplied by the number of steps in each interval, in other words, interval length. We wished skeletons could be as detailed as possible, so we let step length equal to the minimum value ${\rho }_{max}$; therefore, in this research, we would give the method of stump adjustment, so we let the number of steps in each interval equal to the minimum value 2. On the negative side, it produces some breakpoints. These breakpoints exist in alternate positions between intervals and influence a small range of topology, so we gave a simple way of breakpoint connection as follows, where a bin (or a branch segment) is the point set of a local branch near a skeleton point, and initially, each skeleton point is centroid of a bin (it should be noted that the plural of “bin” is bin-s, and a bin means the point set consisting of bin-s of the same layer according to definitions given by Xu et al. [15]).

1.

Because skeleton lines are stored by ordered pairs, they can be regarded as directed edges in graph theory. Therefore, the indegree and outdegree of vertex corresponding to each skeleton point can be computed. Apart from the same vertex as the source vertex, any vertices where indegree is 0 are vertices corresponding to breakpoints.

2.

For each breakpoint, use a kd-tree and k-Nearest-Neighbors (k-NN) search to find 3 neighbor points for which corresponding vertices are not on the tree, with the root being the vertex corresponding to the breakpoint. Compute the number of intersections between bin of breakpoints and bin of each neighbor point. We regarded that a neighbor point that the bin of which has the maximum number of intersections and the number is not equal to 0 should be the same point as the breakpoint. Then, the two points and their corresponding bin-s are required to be merged. If all numbers are equal to 0, directly connect the nearest one to the breakpoint.

This method of breakpoint connection is not optimized, but the following bifurcation optimization and skeleton smoothness can further optimize the skeleton as well. At last, although there are usually no circles in the skeleton, the process of breaking circles is needed in case of potential bad situations. Due to particularity of the produced skeleton, it can be simply described that in directed graph formed by the skeleton, if a vertex where indegree is more than 1, only one edge ending at it should be reserved, and such an edge should have the most comprehensive information branch information.

2.3. Skeleton Optimization

2.3.1. Stump Adjustment

In principle, if a branch is near horizontal and many points on its surface are in the same section of heights, the skeleton points of the branch produced by GC algorithms layering by heights will abruptly shift and not distribute according to the growth direction any more. In addition, there is hardly any tree in which all the segments of the branches are almost straight up. Unless there is reconstruction, the results caused by the defect can no longer be further refined even after optimization. Compared with layering by heights, layering by shortest-path distances can avoid this defect and its result has lower central deviation in general. However, as the shortest-path graph formed by the branch point is in the shape that spreads from the source vertex, the closer the distance is, the more radial the shape can be. Because the source point is on the surface of trunk, the skeleton point closer to the source point is more offset from the center of the trunk. In addition, when the step length is smaller, the center deviation here is more obvious. Point cloud at the stump could be complete or incomplete, not only affected by the process of filtering the ground points but also by undergrowth vegetation during scanning. If the point cloud at the stump is incomplete, the stump would not seem to be cut from a plane visually. When the step length is small, the interval of the branch point cloud near the stump might be clustered erroneously into more than one cluster and subsequently some unwanted branches would probably be produced. That is to say, the skeleton has terrible local distortion at the stump.

You [17] proposed a method to process the branch point cloud at the stump in advance so that a horizontal section can be found, and points below the section in the branch point cloud should be removed by repeatedly calculating the variance of lines connecting the centroids of adjacent horizontal layers below a certain height. Essentially, the method does not solve the problem of center deviation at the stump actually. Other than that, we had not found any other attempts to solve this problem.

We proposed a method to handle the issue without making any changes to the input branch point cloud. This method is processed after the initial skeleton is produced, so it belongs to skeleton optimization, and we named the process of reconstructing the local skeleton at the stump as stump adjustment. Reconstruction means redoing skeleton extraction. It contains three problems: which algorithm for skeleton extraction should be used, which part of the branch point cloud should be chosen as an input and how to replace the original corresponding part with the reconstruction result.

(1) About the chosen algorithm for skeleton extraction.

The way of layering by heights can work relatively normally when producing the skeleton close to the ground because there are not too many bifurcations near the ground in tall trees compared to their crowns. If one input of ISTTWN algorithm is changed from shortest-path distances into heights, the program will run but keep making the wrong progress, as Figure 4 shows. Xu et al.’s [15] algorithm, which used MST algorithm to obtain skeleton lines, can also use the input of heights (similar to Gao’s [16] algorithm) but is easy to create an incorrect topology as MST only guarantees the minimum sum of weights rather than the match between topology and the point cloud. Figure 5 shows a wrong result if Xu et al.’s [15] algorithm is directly used to reconstruct a stump. It is illustrated that algorithms should consider the existence of some branches with abnormal growth direction and of some tree species with ground branching characteristics.

We modified the creation of the graph in Xu et al.’s [15] algorithm according to hierarchical relationship, which is similar to that which TreeQSM uses but more strict than it as we also used the bin information to prevent the unreasonable connection among adjacent layers, and this can satisfy the requirements, as is shown in Algorithm 1.

Algorithm 1 Graph formed according to hierarchical relationship

Input: Skeleton point sequence ${\left\{{\mathit{q}}_n\right\}}_{n=1}^{\mid Q\mid }$, where $\left|Q\right|$ is the size of skeleton point set; Bin   sequence ${\left\{B_n\right\}}_{n=1}^{\mid Q\mid }$ corresponding to each skeleton point in turn; Layer number sequence   ${\left\{L_n\right\}}_{n=1}^{\mid Q\mid }$ corresponding to each skeleton point in turn; Output: Undirected connected graph $G^{\prime }$; 1: $eps:=r_{min}+\epsilon$ ▹$r_{min}$ is the smallest search radius that can make the graph formed by point cloud connected, and $\epsilon$ is infinitesimal as the feasible region of radius search generally does not calculate the boundary 2: Initialize $G^{\prime }$, where $G^{\prime }.V=\{v_1,v_2,\cdots ,v_{\mid Q\mid }\}$ 3: for $i:=1\to \mid Q\mid$ do 4:       Find all vertices that the layer number of corresponding skeleton points is $L_i-1$ and constitute set U 5:     foreach vertex $v_j\in U$ do 6:         if minimum cluster interval between $B_i$ and $B_j$ is less than $eps$ then 7:              $G^{\prime }.E\leftarrow G^{\prime }.E\cup \left\{(v_j,v_i)\right\}$ 8:         end if 9:     end for 10: end for

There are relatively fewer circles in the created graph, and at this time, the accuracy of MST algorithm is obviously better. Because the graph is undirected, edges in the graph need to be oriented to obtain the skeleton.

(2) About the chosen part of the branch point cloud.

In nature, some trees have prop roots and a few of their stumps are especially far from the ground. In order to cater to these trees, we chose a maximum datum height near breast height (1.3 m). Certainly there are some small trees, and the maximum datum height is found near 1.3 m/5 m * tree height when tree height is less than 5 m. In addition, the datum maximum height should be an integral multiple of the set layer height (when layering by heights, step length in the algorithm for skeleton extraction is called as layer height) in avoidance of the uneven height of each layer. The point cloud below this datum height is used as the input to reconstruct the local skeleton.

(3) About the replacement method.

Initially, the current datum height is the maximum datum height. When the current datum height is specified, the direction of local part of branches should be identified. However, such as willow trees, some branches bend over to the earth and their point cloud should be filtered out. In the rest trunk point cloud, for ensuring the reconstructed part can find a common part of the initial skeleton to be connected, the number of bin within the range of adding a layer height to the current datum height should be the same as the number of bin within the range of the current datum height minus a layer height. In addition, a bin in the lower layer should connect to a bin in the higher layer without repetition. The direction of local skeleton lines across the current datum height should also be from low to high. If not making all these conditions tenable, the current datum height will be itself minus a layer height and be retried until it is equal to the lowest height of point cloud plus layer height. Otherwise, reconstruction will be executed. Remove all the skeleton points and lines related to them from the initial skeleton lines, and piece it to the reconstructed local skeleton with the disconnected positions corresponding to each other.

It is obvious that the algorithm for stump adjustment we proposed reconstructs the stump based on layer and hierarchical relationship. It is worth noting that there are four major reasons for reconstruction failure, and stump adjustment can work normally by avoiding them:

(1)

The layer height is too large.

(2)

The tree species could be shrub.

(3)

The point cloud quality is bad.

(4)

Ground normalization has not been performed.

2.3.2. Bifurcation Optimization

We proposed an algorithm for bifurcation optimization based on local branch point cloud and cosine correlation. The principle is based on the characteristics of local branch point cloud covariance matrix. Let ${\mathit{c}}_i$ be the centroid of bin $S_i$ and construct the covariance matrix

$$M_i=\frac{1}{|S_i|}\sum _{\mathit{p}\in S_i}(\mathit{p}-{\mathit{c}}_i){(\mathit{p}-{\mathit{c}}_i)}^{\mathrm{T}}.$$

(2)

The eigenvector corresponding to the maximum eigenvalue of matrix $M_i$ describes the growth direction of the local branch [39]. It should be noted that such eigenvector has ambiguity, in other words, the growth direction may be along the positive or negative direction of the eigenvector.

Let the growth directions of a branch and one of its offshoots at the bifurcation and actual direction of local skeleton lines be $\mathit{v},{\mathit{v}}^{\prime },\mathit{\tau },{\mathit{\tau }}^{\prime }$, respectively. The directions of skeleton lines are completely along the growth directions of the tree if and only if

$$\mathit{v}=k\mathit{\tau },{\mathit{v}}^{\prime }=k^{\prime }{\mathit{\tau }}^{\prime },$$

(3)

where $k\ne 0,k^{\prime }\ne 0$. That is to say, angle $\langle \mathit{v},\mathit{\tau }\rangle =0^{\circ }$ or ${180}^{\circ }$ and angle $\langle {\mathit{v}}^{\prime },{\mathit{\tau }}^{\prime }\rangle =0^{\circ }$ or ${180}^{\circ }$. Using the formula of the cosine value of the angle between two vectors, another form of conclusion can be derived as follows:

$$\left|\frac{\mathit{\tau }\mathit{v}}{{∥\mathit{\tau }∥}_2{∥\mathit{v}∥}_2}·\frac{{\mathit{\tau }}^{\prime }{\mathit{v}}^{\prime }}{{∥{\mathit{\tau }}^{\prime }∥}_2{∥{\mathit{v}}^{\prime }∥}_2}\right|=1.$$

(4)

However, this formula is extremely difficult to hold. So, bifurcation optimization is to find a relatively best connection, in other words, to solve optimization problem

$$\underset{\mathit{\tau },{\mathit{\tau }}^{\prime }}{argmax}\left|\frac{\mathit{\tau }\mathit{v}}{{∥\mathit{\tau }∥}_2{∥\mathit{v}∥}_2}·\frac{{\mathit{\tau }}^{\prime }{\mathit{v}}^{\prime }}{{∥{\mathit{\tau }}^{\prime }∥}_2{∥{\mathit{v}}^{\prime }∥}_2}\right|.$$

(5)

This is a method based on cosine similarity.

When the bifurcation node, its parent node and one of its son nodes are, respectively, $B(x,y,z),A(x_1,y_1,z_1),C(x_2,y_2,z_2)$, the target is to find a B to maximize the cosine similarity. In avoidance of abrupt line trend, B should be in a feasible region D, and the problem can be changed into finding the solution that makes the function

$$f(x,y,z)=\frac{{\left[{\mathit{v}}_1(x-x_1)+{\mathit{v}}_2(y-y_1)+{\mathit{v}}_3(z-z_1)\right]}^2{\left[{{\mathit{v}}^{\prime }}_1(x_2-x)+{{\mathit{v}}^{\prime }}_2(y_2-y)+{{\mathit{v}}^{\prime }}_3(z_2-z)\right]}^2}{({\mathit{v}}_1^2+{\mathit{v}}_2^2+{\mathit{v}}_3^2)({{\mathit{v}}^{\prime }}_1^2+{{\mathit{v}}^{\prime }}_2^2+{{\mathit{v}}^{\prime }}_3^2)\left[{(x-x_1)}^2+{(y-y_1)}^2+{(z-z_1)}^2\right]\left[{(x_2-x)}^2+{(y_2-y)}^2+{(z_2-z)}^2\right]}$$

(6)

reach the maximum value in the feasible region $(x,y,z)\in D$, where the absolute value is eliminated by means of square. However, this problem is difficult to solve because the feasible region is not always in the same shape or can be expressed in the same form, and when using Lagrange multiplier approach, it is very difficult to invert the parameters by making all derivative functions obtained after the derivation of different variables equal to 0. Although the approximate solution of the equation can be found by sampling the feasible region in a certain way, the position of B is not always fixed. Sometimes, when the parent node of B, its grandparent node, …, even a point on lines ending at these points is B, a better solution can be found. With the change in B, if the shape of the feasible region maintains a single form of expression, it is likely to produce an overfitting phenomenon, that is, to find a point that maximizes the value of the equation but has abrupt connections.

In ISTTWN algorithm, a skeleton point is the centroid of a bin. The number of bin-s ECE clusters points into is decided by whether the points can be clearly divided. This feature illustrates that the line between a bifurcation node and its parent node basically goes through the center of the local branch and the production of the bifurcation point is always late. So, we adopted a method to find the relatively most suitable bifurcation point among test points on the broken lines of the local parent branch instead of reconstructing these lines. Figure 6 shows the complete process.

Here are two problems that need to be further discussed.

(1) How are bin-s of three continuous skeleton points divided into two bin-s and then substituted into the equation?

Similarly, let the three skeleton points be $A,B,C$. Construct plane $\Pi$ whose normal vector is $\overrightarrow{AC}$ and passes through point B. Use plane $\Pi$ to divide the point cloud constituted by bin-s of $A,B,C$ into two bin-s.

(2) What is the bin of a broken point?

The bin of a broken point can derive from bin-s of points on both ends of the original line, and the range should be within the range of plus or minus one step length along the direction of the original skeleton line in avoidance of unceasingly accumulating bin-s when encountering too many continuous bifurcations.

2.3.3. Pruning Twigs

As $MinPts$ is set to 1, there are too many small twigs in the skeleton affected by noise points. The following two types of branches are regarded as twigs to be pruned:

(1) If the end point is located in a branch at the top of the tree and the number of its bin is less than the newly specified minimum cluster size, remove the skeleton line connected with the current end point and remove the end point and its bin;

(2) If the skeleton lines that represent one branch at the end of the tree top are less than the specified minimum number of skeleton lines of the branch, the branch shall be removed.

If a branch meets the conditions of (1) and (2) at the same time, it shall be processed according to (2). In this research, the minimum cluster size and the minimum number of skeleton lines of the branch are 4 and 2, respectively.

2.3.4. Skeleton Smoothness

We adopted the method proposed by Xu et al. [33] to smooth the skeleton. For each node ${\mathit{p}}_{\left(2\right)}$ not at both ends of a branch, find its parent node ${\mathit{p}}_{\left(1\right)}$ and its unique son node ${\mathit{p}}_{\left(3\right)}$, and after the k-th iteration,

$${\mathit{p}}_{\left(2\right)}^{\left(k\right)}=\frac{\lambda }{2}{\mathit{p}}_{\left(1\right)}^{(k-1)}+(1-\lambda ){\mathit{p}}_{\left(2\right)}^{(k-1)}+\frac{\lambda }{2}{\mathit{p}}_{\left(3\right)}^{(k-1)},$$

(7)

where the nodes are points in the initial skeleton when $k=0$, $\lambda$ is a coefficient to balance the smoothness result. In this research, the maximum k was set as 5 and $\lambda$ was set as 0.1.

3. Results

3.1. Computational Performance

We tested each part when each experimental material was used as an input to obtain the final optimized skeleton. The basic information about the three tree point clouds, parameters or outputs is shown in

Table 1. Basic information.

Tree Species	Size of Original Tree Point Cloud	Number of Duplicate Points	$\mathit{\rho }$	Size of Branch/Leaf Point Cloud	${\mathit{\rho }}_{max}$ of Branch Point Cloud	Number of Edges in Constructed Undirected Graph
European ash	97,895	0	0.016659 m	94,021/3874	0.166197 m	14,582,170
European oak	836,636	4	0.005627 m	819,556/17,076	0.056221 m	164,547,719
American black poplar	565,698	288,680	0.011883 m	274,688/2330	0.118744 m	70,006,006

. The running time of each part and the change in the skeleton lines are shown in Figure 7. The number of the identified branches is shown in

Table 2. The change in the identified branches.

Tree Species	ISTTWN	Stump Adjustment	Bifurcation Optimization	Pruning Twigs	Skeleton Smoothness
European ash	244	138	183	67	67
European oak	1036	518	674	257	257
American black poplar	705	508	731	268	268

.

The result shows that the processing time is positively proportional to the size of the point cloud in general. As the branch point cloud of the European oak has a relatively sky-high cloud density, the quantity of the points near the earth is quite a lot and it burdens the process of the stump adjustment, which leads to a sudden increase in the time requirement. The time in extracting the other two point clouds is almost the same as the following optimizing process. In addition, the reason why the skeleton lines decrease significantly after the bifurcation optimization is that the algorithm designed for combining broken lines in Figure 6h also combines two normal skeleton lines with a too small included angle in order to retain the necessary topology. The great changes in the number of branches after the stump adjustment will be explained after the visualization in the following section.

3.2. Visual Analysis

The skeletons before optimization and after optimization are shown in Figure 8. Three details were selected on the skeleton of each experimental material. In addition, the skeleton and point cloud are superimposed at these detailed positions to visually check the matching degree between them.

It can be seen from Figure 8 that before the optimization, the distortion of the initial skeletons at the stump is large. The center deviation is almost unavoidable when the skeletons are fine enough, and sometimes unreasonable branches exist, which causes severe topological errors. After the optimization, the unreasonable branches are eliminated successfully, and the corresponding skeleton points are judged as to whether they are removed or retained according to the connection relation. However, the center deviation seems to decrease more or less. It should be illustrated that there is a certain inclination in the point cloud of the European oak; therefore, the result after the stump adjustment is relatively worse than the others visually, while such a result indeed reaches the best in the vertical direction. However, like the point cloud of the American black poplar, the points at the trunk with a near vertical distribution and completely no group part can be processed very well and have a good visual effect.

At bifurcations, although skeletons before the optimization are corresponding to the approximate growth direction, the lines do not go through the center of the bin-s, which bring a stiff felling. The optimized skeletons in the same place are obviously close to the center.

The process of pruning twigs and skeleton smoothness can make skeletons tidier, more beautiful and more natural on the condition that the skeleton lines match the bin-s.

In all, after the optimization in the four aspects we proposed or used, the visual effect of the skeleton is improved, and the errors in the initial skeletons are corrected, which means that the usability of the skeleton is enhanced.

3.3. Application

As the process of obtaining and modifying skeletons follows a basic rule that the fitting is completely unused, these skeletons can be regarded as the true portrayal of the topological structure of trees. Therefore, some parameters about branches of a tree can be extracted. In this research, we computed the branching angle [40] (or bifurcation angle [41], BA), the deflection angle of the branch tip [42] $\theta$ which relates to the size of the branch angle [43] $\Theta$ formed with the vertical direction of the trunk, the distance from the branch tip (or Branch Chord Length [44], BCL) and the branch length (BL) of each first-order branch. Figure 9 gives intuitive definitions of the relevant concepts.

We used evaluation indexes, including the Root Mean Squared Error $RMSE$, Mean Absolute Error $MAE$, Mean Absolute Percentage Error $MAPE$ and coefficient of determination (R-squared) $R^2$, to evaluate the accuracy. The following is the definition formula of each index:

$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n\left(x_i-{\widehat{x}}_i\right){}^2},$$

(8)

$$MAE=\frac{1}{n}\sum _{i=1}^n\left|x_i-{\widehat{x}}_i\right|,$$

(9)

$$MAPE=\frac{100\%}{n}\sum _{i=1}^n\left|\frac{x_i-{\widehat{x}}_i}{x_i}\right|,$$

(10)

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n}\left(x_i-{\widehat{x}}_i\right){}^2}{{\displaystyle \sum _{i=1}^n}\left(x_i-\overline{x}\right){}^2},$$

(11)

where $x_i$ is a real measured certain attribute value of the i-th branch, ${\widehat{x}}_i$ is a certain attribute value of the i-th branch obtained by the skeleton and $\overline{x}$ is the mean value of a certain attribute value of all the branches.

The scatter plot of each branch attribute is constructed with the real values as the x-axis and the corresponding values obtained from the skeleton as the y-axis, as shown in Figure 10.

Table 3. Accuracy of attribute values of branches.

Evaluation Indexes	BA	$\mathit{\theta }$	BCL	BL
$RMSE$	0.164641 (${9.43323}^{\circ }$)	0.086456 (${4.95359}^{\circ }$)	0.203494 m	0.192263 m
$MAE$	0.124162 (${7.11395}^{\circ }$)	0.061605 (${3.52970}^{\circ }$)	0.129652 m	0.125959 m
$MAPE$	13.513%	9.4927%	5.6421%	6.9631%
$R^2$	0.684622	0.896877	0.986168	0.988428

shows the accuracy of the attribute values of the branches. Among them, the BA and $\theta$ use the angle system, which are converted to the radian system before calculating the evaluation indexes.

The $R^2$ of the BA is relatively the lowest, and its $MAE$ is about $7^{\circ }$. This is because measuring the BA manually is measuring the inner edge of two branches with a protractor, while the BA extracted from the skeleton uses almost the centerlines of the local branches. In addition, the size of the protractor affects the accuracy, while the line lengths of the skeleton similarly are affected. Therefore, the BA itself is relatively not a strictly defined quantity. As we used the parameter that makes the skeleton fine enough, the extracted results would be generally more accurate if the BA could be considered as the included angle of the centerlines.

The $R^2$ of the others illustrates that these extracted quantities are basically corresponding to the measured $MAPE$s, indicating that the models are very good. However, it should be noticed that the skeleton of an offshoot always includes a short part on its parent offshoot, and points at treetops are sporadic, which makes the skeleton points at treetops probably deviate the distance up to one step length. These potential errors propagate and cause the $RMSE$ and $MAE$ of the BL to be beyond one step length, and affect the $\theta$ and BCL. So, as the skeleton is good at expressing distances and angles, these quantities can be extracted well, but they still have room for further improvement.

4. Discussion

4.1. Quantitative Analysis and Comparison

We used the three matrices proposed by Xu et al. [33] to evaluate the skeletons themselves quantitatively, including the completeness $A_p$, correctness $A_r$ and effectiveness $A_e$. $A_p$ is equal to the proportion that the union of the local branch point cloud where all the skeleton points are located covers the whole branch point cloud; $A_r$ is equal to the proportion of skeleton points inside the space formed by the local branch point cloud; and $A_e$ is equal to the proportion of skeleton points very close to the center of the local branch point cloud. It should be noted that the local branch point cloud where the skeleton points are located no longer uses the foregoing bin-s but is obtained from the surrounding sphere again. $A_p$ measures how much the skeleton represents the branch point cloud. $A_r$ measures whether the skeleton conforms to the general trend of the branches. And $A_e$ measures whether the skeleton nearly passes through the center of the branch on the basis of $A_r$. The average results of the three values obtained by the selected trees are compared with the average results obtained by theirs. The results are shown in

Table 4. Quantitative analysis.

Matrix	AdTree [45]	Xu et al. [33]	This Research (Before Optimization)	This Research (After Optimization)
Average $A_p$	81.10%	86.99%	97.84%	97.82%
Average $A_r$	99.21%	99.49%	95.20%	95.72%
Average $A_e$	79.26%	36.41%	86.22%	89.47%

.

It can be seen that due to the good feature that the ISTTWN algorithm makes full use of the branch point cloud, the requirement of completeness and effectiveness can be guaranteed in the initial skeletons. However, before the skeleton optimization, the skeleton bifurcates with hysteresis, so this value is slightly low. After the optimization, the skeleton lines decrease obviously, and after the combination, part of the skeleton lines become longer. So, it is normal for $A_p$ to decrease slightly. A higher $A_p$ means that our method is more complete in the expression of the canopy details. However, due to the sparse canopy points, it is easy to cause the wrong identification and classification. $A_r$ will be affected by this factor, resulting in a situation slightly inferior to the other two. When the total of the skeleton points as the denominator decreases, the augment of $A_r$ and $A_e$ reveals that the skeleton is going to be finer. Therefore, the results of both the visual analysis and quantitative analysis show that the skeleton optimization proposed in this study is indeed effective and necessary, and it can improve the results of the ISTTWN algorithm.

4.2. Prospect

In terms of data source, wind disturbance during scanning and severe occlusion of the obtained point cloud will cause errors in tree reconstruction [46]. The corresponding processing technology needs further development.

There are some possible improvements in the complete process of skeletonization. Firstly, a better and highly compatible algorithm for separating the branches and leaves should be developed. Secondly, a dynamic method to construct the shortest-path distances is required as currently the paths constructed by a fixed search radius at different density positions are not always reasonable. Thirdly, as the previous research described, a more efficient allocation method of multithreading can further accelerate the execution. Lastly, research from the aspect of various skeleton optimizations allows for endless topics.

There was some research about more tree parameters extracted from skeletons or a subsequent generalized cylinder model, which are meaningful to forestry, for example, the inclination angle IA [47], azimuth [43] and above-ground biomass [48]. Including the parameters we discussed before, these concepts need to be more clearly defined mathematically and universally acknowledged when skeleton extraction is used. In addition, limited to the current extraction of the main trunk skeleton only referring to angles [49], the results of the branch display at all levels and the parameter extraction of any trees are not available with complete automation and a more suitable extraction method should be further explored.

5. Conclusions

In this research, we proposed and used several methods of skeleton optimization based on the results of the ISTTWN algorithm and the principle of not using fitting. Specifically, it includes the following aspects.

(1)

Different from the existing aspects of skeleton optimization, a stump adjustment is proposed according to the feature at the stump of the tree skeletons layering by the shortest-path distances. An algorithm for reconstructing the stump based on the layer and hierarchical relationship is designed correspondingly.

(2)

From the aspect of bifurcation optimization, an algorithm based on the local branch point cloud and cosine correlation is proposed.

(3)

Pruning twigs and Xu et al.’s [33] skeleton smoothness are adopted in the process of optimization.

With this optimization scheme, the skeletons can be neat, natural and fit with branch point clouds in the visualization. Optimized skeletons are used to extract some branch attributes and evaluate the accuracy. Relatively, the deflection angle of the branch tip, distance from branch tip and branch length can be accurately extracted with strong correlations ($R^2=0.897$, $R^2=0.986$ and $R^2=0.988$, respectively). The availability of the skeletons has been improved, which reveals that this research can help further explore the application scope of tree skeletons.