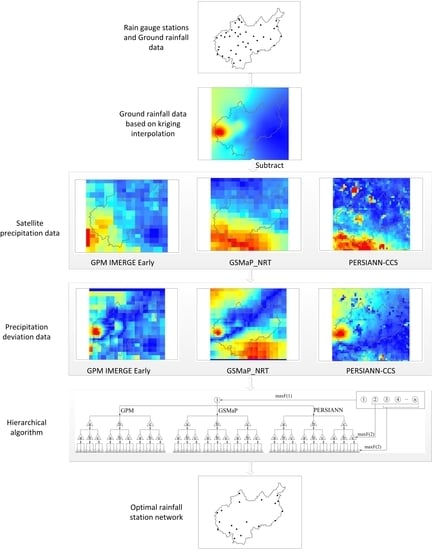
Optimal Rain Gauge Network Design Aided by Multi-Source Satellite Precipitation Observation
Abstract
:1. Introduction
2. Method
2.1. Kriging Interpolation Technique
2.2. Information Entropy
2.3. Hierarchical Algorithm
3. Study Area and Dataset
3.1. Study Area
3.2. Dataset
3.2.1. Daily Precipitation Data from Existing and Virtual Rain Gauge Stations
3.2.2. Satellite-Observed Daily Precipitation Data
3.2.3. Daily Precipitation Deviation Data Set
4. Experiments and Results
4.1. Existing Rain Gauge Station Network Optimization
4.2. Rain Gauge Station Network Optimization Considering Virtual Stations
5. Discussion
5.1. Comparative Analysis of Rain Gauge Station Network Optimization Design Results
5.2. Comparison of Maximum Joint Information Entropy with Different Rain Gauge Stations
5.3. Analysis of Satellite Precipitation Deviation Interpolation Accuracy
5.4. Information Entropy Correlation Analysis of Satellite Precipitation Deviation
6. Conclusions
- (1)
- Most of the entropy-based network optimization studies use the rainfall data of rain gauge stations to retain more information and reduce information redundancy. The entropy measure for satellite and ground rainfall deviations is more meaningful and more explanatory. The magnitude of entropy of the rainfall deviations not only expresses the amount of information, but also reflects that some locations are more difficult to measure, and these locations are often affected by topography and geomorphology, and stations should be established here.
- (2)
- Of the three satellite precipitation data, PERSIANN−CCS has the highest spatial resolution. Compared with GPM IMERGE Early and GSMap_NRT, PERSIANN−CCS has more obvious differences in the spatial distribution of precipitation deviation and information entropy, and the calculated joint entropy value is also the largest, which has unique advantages for rain gauge network optimization.
- (3)
- A large number of studies have shown that through various statistical interpolation and machine learning algorithms, satellite precipitation data and ground rainfall data are fused, and the reprocessed data obtained has the advantages of high precision and high resolution. The use of this kind of fused data for rain gauge network optimization is a worthy study in the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Wagner, P.D.; Fiener, P.; Wilken, F.; Kumar, S.; Schneider, K. Comparison and evaluation of spatial interpolation schemes for daily rainfall in data scarce regions. J. Hydrol. 2012, 464–465, 388–400. [Google Scholar] [CrossRef]
- Tiwari, S.; Jha, S.K.; Singh, A. Quantification of Node Importance in Rain gauge station network: Influence of Temporal Resolution and Rain Gauge Density. Sci. Rep. 2020, 10, 9761. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.; Sælthun, N.R.; Xu, Y.; Zhou, B.; Chen, H. Entropy Theory Based Multi-Criteria Resampling of Rain gauge station networks for Hydrological Modelling—A Case Study of Humid Area in Southern China. J. Hydrol. 2015, 525, 138–151. [Google Scholar] [CrossRef]
- Stosic, T.; Stosic, B.D.; Singh, V.P. Optimizing streamflow monitoring networks using joint permutation entropy. J. Hydrol. 2017, 552, 306–312. [Google Scholar] [CrossRef]
- Leach, J.M.; Kornelsen, K.C.; Samuel, J.; Coulibly, P. Hydrology Network Design Using Streamflow Signatures and Indicators of Hydrologic Alteration. J. Hydrol. 2015, 529, 1350–1359. [Google Scholar] [CrossRef]
- Su, H.; You, G.J. Developing an Entropy-based Model of Spatial Information Estimation and Its Application in the Design of Precipitation Gauge Networks. J. Hydrol. 2014, 519, 3316–3327. [Google Scholar] [CrossRef]
- Li, H.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wu, J. Developing an entropy and copula-based approach for precipitation monitoring network expansion. J. Hydrol. 2021, 598, 126366. [Google Scholar] [CrossRef]
- Yeh, H.C.; Chen, Y.C.; Wei, C.; Chen, R.H. Entropy and Kriging approach to Rainfall Network Design. Paddy Water Environ. 2011, 9, 343–355. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Yilmaz, A.G.; Muttil, N. Optimal Design of Rain gauge station network in the Middle Yarra River Catchment, Australia. Hydrol. Process. 2015, 29, 2582–2599. [Google Scholar] [CrossRef]
- Safavi, M.; Siuki, A.K.; Hashemi, S.R. New optimization methods for designing rain stations network using new neural network, election, and whale optimization algorithms by combining the Kriging method. Environ. Monit. Assess. 2021, 193, 4. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula Based Multisite Model for Daily Precipitation Simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef] [Green Version]
- Vivekanandan, N.; Jagtap, R.S. Evaluation and Selection of Rain gauge station network using Entropy. J. Inst. Eng. 2012, 93, 223–232. [Google Scholar]
- Feki, H.; Mohamed, S.; Cudennec, C.H. Geostatistically based optimization of a precipitation monitoring data network extension: Case of the climatically heterogeneous Tunisia. Hydrol. Res. 2017, 48, 514–541. [Google Scholar] [CrossRef]
- Ali, M.Z.M.; Othman, F. Rain gauge station network optimization in a tropical urban area by coupling cross-validation with the geostatistical technique. Hydrol. Sci. J. 2018, 63, 474–491. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.Y.; Chen, H.; Zhang, Z.; Li, L. Assessing the Influence of Rain gauge Distribution on Hydrological Model Performance in a Humid Region of China. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- Cetinkaya, C.P.; Harmancioglu, N.B. Reduction of Streamflow Monitoring Networks by a Reference Point Approach. J. Hydrol. 2014, 512, 263–273. [Google Scholar] [CrossRef]
- Kar, A.K.; Lohani, A.K.; Goel, N.K.; Roy, G.P. Rain gauge station network Design for Flood Forecasting Using Multi-Criteria Decision Analysis and Clustering Techniques in Lower Mahanadi River Basin, India. J. Hydrol. 2015, 4, 313–332. [Google Scholar]
- Fahle, M.; Hohenbrink, T.L.; Dietrich, O.; Lischeid, G. Temporal Variability of the Optimal Monitoring Setup Assessed Using Information Theory. Water Resour. Res. 2015, 51, 7723–7743. [Google Scholar] [CrossRef] [Green Version]
- Chacon-Hurtado, J.C.; Alfonso, L.; Solomatine, D.P. Rainfall and Streamflow Sensor Network Design: A Review of Application, Classification, and a Proposed Framework. Hydrol. Earth Syst. Sci. 2017, 21, 3071–3091. [Google Scholar] [CrossRef] [Green Version]
- Keum, J.; Coulibaly, P. Information Theory-based Decision Support System for Integrated Design of Multi-variable Hydrometric Network. Water Resour. Res. 2017, 53, 6239–6259. [Google Scholar] [CrossRef]
- Keum, J.; Kornelsen, K.C.; Leach, J.M.; Coulibaly, P. Entropy Applications to Water Monitoring Network Design: A Review. Entropy 2017, 19, 613. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, X.; Chen, L.; Yuan, X.; Dong, H.; Yu, Y. Optimization of The Basin Hydrologic Network Based on Multi-objective Criteria. J. Hohai Univ. Nat. Sci. 2019, 47, 102–107. [Google Scholar]
- Wang, W.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Zhang, J.; Liu, J.; Zou, Y.; He, R.; Meng, D. Evaluation of Information Transfer and Data Transfer Models of Rain gauge station network Design Based on Information Entropy. Environ. Res. 2019, 178, 108686. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. Entropy Theory-based Criterion for Hydrometric Network Evaluation and Design: Maximum Information Minimum Redundancy. Water Resour. Res. 2012, 48, W05521. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Optimization of Water Level Monitoring Network in Polder Systems Using Information Theory. Water Resour. Res. 2010, 46, W12553. [Google Scholar] [CrossRef]
- Husain, T. Hydrologic Uncertainty Measure and Network Design. Water Resour. Bull. 1989, 25, 527–534. [Google Scholar] [CrossRef]
- Meng, C.; Mo, X.; Liu, S.; Hu, S. Extensive Evaluation of IMERGE Precipitation for Both Liquid and Solid in Yellow River Source Region. Atmos. Res. 2021, 256, 105570. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Zhu, Y.; Gui, Y.; Wang, X. Evaluating the hydrological utility of latest IMERGE Products over the Upper Huaihe River Basin, China. Atmos. Res. 2019, 225, 17–29. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERGE and TMPA Version-7 Legacy Products over Mainland China at multiple Spatiotemporal Scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Lu, X.; Tang, G.; Wang, X.; Liu, Y.; Wei, M.; Zhang, Y. The Development of a Two-Step Merging and Downscaling Method for Satellite Precipitation Products. Remote Sens. 2020, 12, 398. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Chen, H.; Tian, B.; Sheng, S.; Wang, J.; Kim, J. A Downscaling-Merging Scheme for Improving Daily Spatial Precipitation Estimates Based on Random Forest and Cokriging. Remote Sens. 2021, 13, 2040. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lu, A.; Yan, T. A Statistical Spatial Downscaling Algorithm of TRMM Precipitation Based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Zhang, Q.; Shi, P.; Singh, V.P.; Fan, K.; Huang, J. Spatial Downscaling of TRMM-based Precipitation Data Using Vegetative Response in Xinjiang, China. Int. J. Climatol. 2016, 37, 3895–3909. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Sheng, S.; Mansaray, L.R.; Liu, Z.; Wu, H.; Wang, X. A New Downscaling-Integration Framework for High-Resolution Monthly Precipitation Estimates: Combining Rain Gauge Observations, Satellite-Derived Precipitation Data and Geographical Ancillary Data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Dai, Q.; Bray, M.; Zhuo, L.; Islam, T.; Han, D.W. A Scheme for Rain Gauge Station Network Design Based on Remotely-sensed Rainfall Measurements. J. Hydrometeorol. 2017, 18, 363–379. [Google Scholar] [CrossRef]
- Yeh, H.C.; Chen, Y.C.; Chang, C.H.; Ho, C.H.; Wei, C. Rainfall Network Optimization Using Radar and Entropy. Entropy 2017, 19, 553. [Google Scholar] [CrossRef] [Green Version]
- Morsy, M.; Taghizadeh-Mehrjardi, R.; Michaelides, S.; Scholten, T.; Dietrich, P.; Schmidt, K. Optimization of Rain Gauge Networks for Arid Regions Based on Remote Sensing Data. Remote Sens. 2021, 13, 4243. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Keum, J.; Coulibaly, P.; Razavi, T.; Tapspba, D.; Gobena, A.; Weber, F.; Pietroniro, A. Application of SNODAS and Hydrologic Models to Enhance Entropy-based Snow Monitoring Network Design. J. Hydrol. 2018, 561, 688–701. [Google Scholar] [CrossRef]
- Ridolfi, E.; Montesarchio, V.; Russo, F.; Napolitano, F. An entropy Approach for Evaluating the Maximum Information Content Achievable by an Urban Rainfall Network. Nat. Hazards Earth Syst. Sci. 2011, 11, 2075–2083. [Google Scholar] [CrossRef] [Green Version]
- Awadallah, A.G. Selecting Optimum Locations of Rainfall Stations Using Kriging and Entropy. Int. J. Energy Environ. Eng. 2012, 12, 36–41. [Google Scholar]
- Mahmoudi-Meimand, H.; Nazif, S.; Abbaspour, R.A.; Sabokbar, H.F. An Algorithm for Optimisation of a Rain gauge station network Based on Geostatistics and Entropy Concepts Using GIS. J. Spat. Sci. 2016, 61, 233–252. [Google Scholar] [CrossRef]
- Papadopoulou, M.; Raphael, B.; Smith, I.F.C.; Sekhar, C. Hierarchical sensor placement using joint entropy and the effect of modeling error. Entropy 2014, 16, 5078–5101. [Google Scholar] [CrossRef]
- Bertola, N.J.; Papadopoulou, M.; Vernay, D.; Smith, I.F.C. Optimal multi-type sensor placement for structural identification by static-load testing. Sensors 2017, 17, 2904. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulou, M.; Raphael, B.; Smith IF, C.; Sekhar, C. Optimal Sensor Placement for Time-Dependent Systems: Application to Wind Studies around Buildings. J. Comput. Civil. Eng. 2016, 30, 4015024. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Chen, W.; Chen, B.; Tan, D.; Zhang, Y.; Shen, D. Robust Hierarchical Sensor Optimization Placement Method for Leak Detection in Water Distribution System. Water Resour. Manag. 2021, 35, 3995–4008. [Google Scholar] [CrossRef]
- Chen, Y.C.; Wei, C.; Yeh, H.C. Rainfall network design using kriging and entropy. Hydrol. Process. 2008, 22, 340–346. [Google Scholar] [CrossRef]
- Wei, C.; Yeh, H.C.; Chen, Y.C. Spatialtemporal Scaling Effect on Rainfall Networks Design Using Entropy. Entropy 2014, 16, 4626–4627. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L. A kriging and entropy-based approach to rain gauge network design. Environ. Res. 2018, 161, 61–75. [Google Scholar] [CrossRef]
- Habib, E.; Henschke, A.; Adler, R.F. Evaluation of TMPA satellite-based research and real-time rainfall estimates during six tropical-related heavy rainfall events over Louisiana, USA. Atmos. Res. 2009, 94, 373–388. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of precipitation estimation between Version 7 3-hourly TRMM Multi-Satellite Precipitation Analysis (TMPA) near-real-time and research products. Atmos. Res. 2015, 153, 119–133. [Google Scholar] [CrossRef] [Green Version]
- Hénin, R.; Liberato, M.; Ramos AGouveia, C. Assessing the Use of Satellite-Based Estimates and High-Resolution Precipitation Datasets for the Study of Extreme Precipitation Events over the lberian Peninsula. Water 2018, 10, 1688. [Google Scholar] [CrossRef] [Green Version]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
- Wu, H.; Chen, Y.; Chen, X.; Liu, M.; Gao, L.; Deng, H. A New Approach for Optimizing Rain gauge station networks: A Case Study in the Jinjiang Basin. Water 2020, 12, 2252. [Google Scholar] [CrossRef]
- WMO (World Meteorological Organization). Guide to Hydrometeorological Practices, Volume I: Hydrology—From Measurement to Hydrological Information (WMO Publication 168, Vol. I); World Meteorological Organization: Geneva, Switzerland, 2008.
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part I—A discussion of principles. J. Hydrol. 1970, 370, 139–154. [Google Scholar] [CrossRef]
- Andréassian, V.; Perrin, C.; Michel, C.; Usart-Sanchez, I.; Lavabre, J. Impact of imperfect rainfall knowledge on the efficiency and the parameters of watershed models. J. Hydrol. 2001, 250, 206–223. [Google Scholar] [CrossRef]
















| Precipitation Products | Number of Retained Stations | Optimized Ranking Results |
|---|---|---|
| GPM | 17 | 12, 19, 25, 40, 1, 34, 7, 11, 2, 33, 35, 32, 26, 13, 6, 4, 3, 17, 9, 10, 18, 36, 24, 22, 38, 28, 8, 30, 5, 16, 14, 15, 31, 37, 27, 20, 21, 23, 29, 39 |
| GSMaP | 19 | 25, 12, 1, 37, 34, 13, 11, 32, 6, 4, 40, 2, 26, 18, 24, 19, 38, 8, 7, 5, 33, 28, 29, 35, 3, 17, 21, 16, 10, 30, 9, 14, 15, 22, 31, 23, 20, 27, 36, 39 |
| PERSIANN | 18 | 25, 3, 40, 12, 34, 7, 19, 9, 6, 13, 33, 8, 32, 26, 2, 38, 20, 35, 30, 5, 1, 24, 18, 28, 36, 17, 22, 4, 14, 37, 10, 21, 23, 31, 29, 39, 11, 16, 27, 15 |
| Combination | 19 | 12, 25, 40, 1, 34, 19, 7, 11, 13, 6, 32, 33, 8, 26, 2, 5, 38, 35, 3, 18, 37, 24, 4, 28, 17, 30, 22, 10, 14, 20, 9, 36, 16, 21, 29, 15, 31, 23, 27, 39 |
| Rain Gauge | 19 | 12, 25, 19, 1, 40, 13, 34, 8, 7, 33, 11, 3, 32, 6, 26, 24, 18, 4, 28, 2, 5, 17, 29, 38, 35, 14, 22, 37, 10, 9, 30, 15, 23, 31, 16, 39, 27, 20, 21, 36 |
| Precipitation Products | Number of Retained Stations | Optimized Ranking Results |
|---|---|---|
| GPM | 20 | 12, 19, 25, 40, 1, 34, 7, 11, 63, 2, 32, 33, 35, 13, 6, 26, 4, 65, 3, 17, 9, 10, 67, 18, 24, 36, 22, 28, 8, 30, 16, 61, 5, 14, 15, 60, 47, 42, 74, 54 |
| GSMaP | 25 | 71, 12, 1, 34, 40, 25, 8, 32, 9, 7, 63, 33, 3, 13, 11, 45, 6, 4, 37, 26, 2, 18, 74, 24, 28, 47, 38, 57, 17, 29, 5, 35, 16, 65, 10, 68, 30, 14, 15, 22 |
| PERSIANN | 19 | 25, 3, 40, 12, 34, 7, 19, 9, 6, 13, 33, 8, 63, 32, 26, 2, 37, 5, 35, 20, 30, 62, 18, 42, 1, 24, 4, 17, 14, 28, 54, 22, 21, 16, 36, 31, 46, 66, 10, 39 |
| Combination | 22 | 12, 25, 40, 1, 34, 19, 7, 11, 63, 13, 6, 32, 33, 8, 2, 26, 5, 35, 18, 3, 37, 4, 24, 65, 28, 17, 74, 45, 30, 22, 9, 14, 16, 57, 20, 42, 10, 67, 62, 36 |
| Rain Gauge | 20 | 71, 12, 19, 1, 34, 40, 7, 8, 25, 13, 11, 33, 3, 6, 26, 4, 18, 32, 24, 28, 2, 5, 17, 29, 38, 14, 22, 35, 37, 10, 9, 30, 15, 23, 31, 16, 39, 27, 73, 20 |
| Optimization of 40 Rain Gauge Stations | Optimization of 75 Rain Gauge Stations | ||||||
|---|---|---|---|---|---|---|---|
| Satellite Combination | Rain Gauge | Satellite Combination | Rain Gauge | ||||
| StationID | Area (km2) | StationID | Area (km2) | StationID | Area (km2) | StationID | Area (km2) |
| 12 | 1604.40 | 12 | 1333.27 | 12 | 1628.26 | 12 | 1769.77 |
| 33 | 1594.85 | 32 | 1298.03 | 33 | 1413.78 | 33 | 1697.74 |
| 35 | 1539.17 | 18 | 1291.90 | 35 | 1359.07 | 32 | 1276.79 |
| 7 | 971.98 | 33 | 1226.63 | 18 | 1035.34 | 18 | 1235.89 |
| 8 | 865.63 | 24 | 1177.67 | 8 | 817.27 | 7 | 940.44 |
| 2 | 814.46 | 7 | 880.68 | 2 | 808.73 | 8 | 794.31 |
| 13 | 791.39 | 34 | 735.51 | 26 | 800.16 | 6 | 724.06 |
| 26 | 769.26 | 6 | 720.30 | 7 | 785.44 | 34 | 706.19 |
| 32 | 748.61 | 1 | 694.81 | 32 | 563.60 | 28 | 678.17 |
| 38 | 661.76 | 8 | 690.43 | 11 | 547.05 | 1 | 668.80 |
| 11 | 543.84 | 11 | 585.88 | 6 | 444.57 | 11 | 571.80 |
| 6 | 452.37 | 28 | 465.00 | 63 | 378.58 | 26 | 340.52 |
| 3 | 356.45 | 26 | 349.20 | 34 | 353.50 | 40 | 315.66 |
| 40 | 310.05 | 13 | 344.95 | 13 | 344.95 | 4 | 286.75 |
| 1 | 291.50 | 40 | 317.85 | 1 | 298.99 | 13 | 272.57 |
| 25 | 281.37 | 4 | 282.43 | 37 | 293.44 | 3 | 266.49 |
| 5 | 207.06 | 3 | 268.75 | 3 | 268.75 | 71 | 202.88 |
| 19 | 194.09 | 25 | 236.27 | 25 | 236.27 | 19 | 194.24 |
| 34 | 104.91 | 19 | 203.59 | 4 | 208.68 | 25 | 160.09 |
| 19 | 203.59 | ||||||
| 40 | 200.55 | ||||||
| 5 | 112.58 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Chen, W.; Hu, Z.; Xu, Y.; Shen, D. Optimal Rain Gauge Network Design Aided by Multi-Source Satellite Precipitation Observation. Remote Sens. 2022, 14, 6142. https://doi.org/10.3390/rs14236142
Wang H, Chen W, Hu Z, Xu Y, Shen D. Optimal Rain Gauge Network Design Aided by Multi-Source Satellite Precipitation Observation. Remote Sensing. 2022; 14(23):6142. https://doi.org/10.3390/rs14236142
Chicago/Turabian StyleWang, Helong, Wenlong Chen, Zukang Hu, Yueping Xu, and Dingtao Shen. 2022. "Optimal Rain Gauge Network Design Aided by Multi-Source Satellite Precipitation Observation" Remote Sensing 14, no. 23: 6142. https://doi.org/10.3390/rs14236142
APA StyleWang, H., Chen, W., Hu, Z., Xu, Y., & Shen, D. (2022). Optimal Rain Gauge Network Design Aided by Multi-Source Satellite Precipitation Observation. Remote Sensing, 14(23), 6142. https://doi.org/10.3390/rs14236142