Evaluating the Use of Lidar to Discern Snag Characteristics Important for Wildlife

Abstract

Standing dead trees (known as snags) are historically difficult to map and model using airborne laser scanning (ALS), or lidar. Specific snag characteristics are important for wildlife; for instance, a larger snag with a broken top can serve as a nesting platform for raptors. The objective of this study was to evaluate whether characteristics such as top intactness could be inferred from discrete-return ALS data. We collected structural information for 198 snags in closed-canopy conifer forest plots in Idaho. We selected 13 lidar metrics within 5 m diameter point clouds to serve as predictor variables in random forest (RF) models to classify snags into four groups by size (small (<40 cm diameter) or large (≥40 cm diameter)) and intactness (intact or broken top) across multiple iterations. We conducted these models first with all snags combined, and then ran the same models with only small or large snags. Overall accuracies were highest in RF models with large snags only (77%), but kappa statistics for all models were low (0.29–0.49). ALS data alone were not sufficient to identify top intactness for large snags; future studies combining ALS data with other remotely sensed data to improve classification of snag characteristics important for wildlife is encouraged.

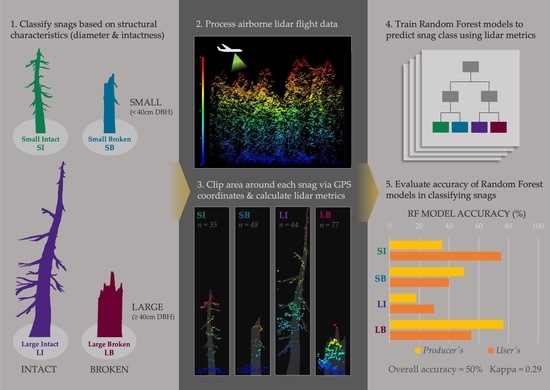
1. Introduction

As keystone structures [1], standing dead trees (hereafter, snags) serve essential roles for wildlife species, due in part to how structurally distinct snags are compared to live trees. Snag and live tree characteristics differ across multiple dimensions, including the degree of open space occupied, the unique physical structures provided, and the composition and decay status of wood. These combined characteristics contribute to a wide range of forest microhabitats relevant to wildlife, with many microhabitats associated primarily with snags [2,3].

In terms of open space, snag presence and breakdown can be central to the generation of gaps within the canopy used by volant organisms as travel corridors [4,5]. Stitt et al. [6] evaluated forest canopy gaps around individual trees to establish that snags were associated with significantly larger gap fractions in the immediate vicinity than live conifer trees, especially at midcanopy heights (5 to 20 m above ground). Snags also had higher variability in gap distributions across all canopy heights [6]. This greater variability in openness around snags contributes to greater forest structural complexity and may be correlated with greater foliar height diversity and species richness [7].

In terms of physical structures, snags add unique microhabitat characteristics to forested landscapes that are not common in live trees. Snags may retain exposed branches on which to perch, which is important for aerial avian flycatchers and birds of prey [8,9,10,11]. Snags may have a broken top that can serve as a nesting platform for management-sensitive species such as northern goshawks (Accipiter gentilis) [12] and great gray owls (Strix nebulosa) [13]. Snag diameter at breast height (DBH) has been found to be a strong predictor of use by wildlife species [2,14,15]. Branches on snags can be colonized by moss and lichens, creating further subsystems within the canopy [16,17]. This greater variability in structural elements associated with snags likely also contributes to greater forest structural complexity in the forms of increased microhabitat diversity and niche availability, leading to greater species richness [7].

In terms of wood composition, dead wood is more suitable than live wood for cavity excavation and nesting opportunities for many species, due to greater decay (resulting from the cessation of tree defenses) [18]. Decaying wood is utilized by insects for foraging and laying eggs, and the insects in turn are foraged by woodpeckers (among other insectivores). As wood decays, it softens, enabling woodpeckers to excavate cavities [18,19,20], and as tree limbs decay, they fall, which may also create sites for natural cavity formation [8,18,21]. Tree microhabitats derived from dead wood, along with other microhabitats created as a tree breaks down (e.g., bark pockets and fissures) [2,17], provide important wildlife habitat that make snags a valuable feature for species mapping and management efforts [2,14,22].

Remote detection of snags is difficult because there is often less information to work with relative to live trees, and because the snag decay process is highly variable. Previous attempts using airborne laser scanning (ALS), or lidar, to identify snags focused on tree crowns as the basis for individual tree segmentation [23,24,25], intensity metrics [26,27,28,29], and topographic features [30]. However, approaches focused upon tree crowns can be challenging with snags because dead trees lack the foliar surface area of live tree canopies, and therefore reflect far fewer laser pulses to evaluate and locate snags [28]. Focusing on the absence of lidar data (in the form of a canopy gap fraction) can provide additional valuable information for characterizing snags from ALS data [6]. Determining what further information can be gleaned from the sparse lidar data associated with snags is an area worth investigating.

Few ALS-based studies have focused solely on snags or attempted to differentiate among them, with previous works having focused on snag DBH and volume estimates [29,31,32]. Some studies have explored spectral signatures in the form of return intensity metrics [28,29,33], but comparisons across sites can be problematic unless the uncalibrated intensity values are normalized. To our knowledge, no other studies have attempted to determine whether ALS data can provide enough information to discern among specific snag characteristics important for wildlife, such as broken versus intact tops.

The focus of this study was to determine whether structural characteristics of snags can be differentiated using ALS data. If differences in structural signatures can be detected via remote sensing, they could be applied to improve mapping efforts and suitability assessments for many wildlife species that depend upon microhabitats related to standing dead trees. In combining field plot survey data with airborne lidar scans, the current study aimed to determine whether the microhabitats of top intactness (intact vs. broken top) and snag size (small: less than 40 cm in diameter vs. large: greater than or equal to 40 cm in diameter) can be described using ALS data. We compared these field-derived structural characteristics against a suite of airborne-lidar-derived metrics.

Our primary hypothesis was that snags of different structural classes (based on diameter and intactness) would produce significantly different airborne lidar structural metrics. We hypothesized that intact snags may have stronger positive correlations with variables such as point density, percent of first returns, and evenness metrics; intact snags have often experienced more recent mortality, and thus are associated with greater residual branching and crown structures that could present more surface area off which to reflect. We also hypothesized that broken top snags may have stronger positive correlations with variables such as percent of third returns, gap fraction, and roughness metrics; broken top snags are associated with less recent mortality events, and thus with more decay and breakdown of structural features that could more resemble open space. We hypothesized that our ability to detect distinct signatures among snag intactness would be influenced by snag diameter and predicted that snags with larger diameters would have stronger correlations with metrics overall, due to a larger surface area and a lesser proportion of surrounding “noise” within the set footprint (2.5 m radius circle around snag center), relative to smaller snags.

2. Materials and Methods

2.1. Study Area

The study was conducted in closed-canopy forest stands within the Idaho Panhandle National Forest (IPNF), Idaho, USA. The study area consisted of two sites within IPNF: one site in the Coeur d’Alene River Ranger District (herein CdA), and one site in the Saint Joe Ranger District (herein StJ; Figure 1). Both sites were composed of mature mixed-conifer forest stands managed for multiple uses, including timber production, recreation, and wildlife habitat [34]. Across both sites, the most abundant species of snags found were grand fir (Abies grandis) and western larch (Larix occidentalis), followed by Douglas fir (Pseudotsuga menziesii) at CdA and western redcedar (Thuja plicata) at StJ.

2.2. Field Data Collection

All snags evaluated for this study were located within 25 m fixed-radius snag survey plots. Survey plot locations were selected through a stratified random sampling design based on canopy cover and height metrics from lidar [35] and constrained using criteria to enable subsequent point count surveys of forest birds, based on existing protocols (e.g., [36,37]) including a 300 m minimum distance from other plot centers and a road buffer (minimum of 60 m and maximum of 250 m away from roads). Plot centers were recorded using a global navigation satellite system (GNSS) receiver (Trimble GeoXH; Sunnyvale, CA, USA) and differentially corrected in postprocessing [36].

Snags identified within a 25 m radius survey plot were measured, provided they satisfied the criteria, including: (1) a minimum height equal to breast height (used to measure diameter at breast height, DBH; 1.37m above ground), (2) a minimum DBH of 0.15 m, (3) less than a 45° lean in any direction, and (4) possessed no visible live parts of the tree (primarily the presence of green needles; red/brown needles were accepted and noted). The minimum DBH was selected based on criteria for woodpecker use (see [14]). Snag locations were recorded using the same GNSS receiver as used for plot center, which was positioned on the north side of the bole.

2.3. Airborne Lidar Data Acquisition and Processing

Discrete-return ALS data were acquired across both sites as part of an ongoing effort by the U.S. Forest Service Rocky Mountain Research Station (USFS RMRS; Moscow, ID, USA) to develop advanced protocols for forest mapping and monitoring. The lidar extent of CdA spanned 78,706 ha to the east of Coeur d’Alene, ID, USA (centered at 47°44′40.0″N, 116°36′38.8″W). The lidar extent of StJ spanned 7598 ha to the east of Avery, ID, USA (centered at 47°08′28.5″N, 116°05′38.9″W). Details on the lidar acquisition parameters can be found in

Table 1. Lidar acquisition parameters. The discrete-return airborne lidar (also airborne laser scanning, ALS) data from the two study sites (based on IPNF Ranger Districts: Coeur d’Alene River, CdA; Saint Joe, StJ) were part of a larger acquisition carried out by USFS RMRS in 2016 (see [36] for more details).

Parameter	Specification
Date collected	12 October 2016
Vendor	Atlantic Group, LLC
Sensor	Leica ALS70-HP
Flight altitude	1965 m above ground level
Flight speed	110 kts
Pulse frequency	278 kHz
Scan frequency	41 Hz
Scan angle	± 30°
Swath width	1098 m
Swath overlap	50%
Laser wavelength	1064 nm
Laser beam divergence	0.22 mrad
Vertical accuracy	5.9 cm
Footprint diameter	43 cm
Nominal pulse density	4.2 pulses/m2

. The georeferenced lidar data were processed at the plot level using the R environment (R Core Team 2020, version 4.0.3). Point clouds were preprocessed using the lidR package [38] at a 50 m radius around plot centers (0.8 ha plots) to generate buffered, height-normalized point clouds. All ground, near-ground, and understory returns below 1.37 m were excluded to retain only canopy returns. Outliers below 50 m height above ground were not removed, as they may represent snag hits.

Snag center coordinates were calculated by subtracting half the measured DBH from the northing value collected in the field, to correct for the GNSS receiver being positioned on the north side of the bole. Snag center coordinates were used as locations to clip the height-normalized ALS point clouds from within each survey plot. Individual snag point clouds were clipped to a 2.5 m circular radius buffer around each snag center, in order to encompass the full tree footprint, offset any error in GPS location, and preserve enough returns to compute all metrics.

2.4. Predictor Variable Selection

Lidar-derived metrics were calculated for each 2.5 m radius snag point cloud, with a minimum height set to 1.37 m above ground. A subset of the full suite of standard height and return-based metrics (as provided in the lidR package; see [38]) was chosen alongside additional structural and topographic metrics for this study, in order to best evaluate differences among the four classes of snag structural characteristics. We focused on lidar metrics previously shown to be effective indicators of forest biomass across different forest types (e.g., [39,40]) and those which would have specific utility for individual snags, as compared to individual live tree or plot-level analyses (

Table 2. Airborne lidar-derived metrics used as predictor variables in RF models to classify snag characteristics of snags measured in Idaho coniferous forests. For additional information on equations and ecological significance of each predictor variable, please see Appendix A Table A1.

Variable	Description
PTDEN	Point density; number of total returns per meter
P1stRN	Percent of first returns (out of total returns)
P2ndRN	Percent of second returns (out of total returns)
P3rdRN	Percent of third returns (out of total returns)
GFPmid	Gap Fraction Profile (GFP), calculated only for midcanopy heights (every 1m between 5 m and 20 m above ground)
LADcv	Leaf Area Density (LAD) coefficient of variance; derived from measures every 2 m across all canopy heights
RUMPLE	Rumple index; roughness of a surface based on ratio between surface area and projected area on the ground
ENTmid	Entropy, calculated only for midcanopy heights (between 5 m and 20 m above ground); normalized Shannon diversity and evenness index
VAI	Vegetation Area Index (VAI); sum of LAD values, derived from measures every 2 m across all canopy heights
VCI	Vertical Complexity Index (VCI); fixed normalization of entropy across heights, derived from measures every 2 m across all canopy heights
ELEV	Elevation (in meters), averaged across the 25 m radius reference plot
SLOPE	Slope (in degrees), averaged across the 25 m radius reference plot
TRASP	Transformed aspect (in degrees), averaged across the 25 m radius reference plot

).

2.5. Random Forest Model Development

To analyze whether airborne lidar metrics could be used to discriminate between snag classes, we conducted random forest (RF) classification using the R environment and with the packages randomForest [41] and caret [42]. For our response variables, we focused on two aspects from field inventory data for each snag: diameter and intactness. We divided the candidate snags into two categories for each of these variables, in order to have distinct groups to compare lidar metrics against. Snag diameter was divided into small (DBH less than 40 cm) and large (DBH greater than or equal to 40 cm) groups, based on literature suggesting these are ecologically relevant distinctions [43], as well as important for ALS detectability [14]. Snag intactness was divided into intact (where the snag bole still had a visible top) and broken (where at least part of the bole had broken off) groups. We therefore had four snag classes for our response variable (Figure 2): “small intact” (SI), “small broken” (SB), “large intact” (LI), and “large broken” (LB). In total, there were 198 snags evaluated across all snag classes (

Table 3. Summary statistics by snag class across all snags (n = 198) measured in conifer forests in Idaho, USA. A breakdown of airborne lidar point density (total returns/area) per snag point cloud is included, with mean (µ) and standard deviation (sd) for each snag class. Snags split by study site are not shown, but overall there were more snags at CdA (n = 141) than StJ (n = 63), driven primarily by a greater number of broken top snags in both size classes.

Diameter	Intactness	Number of Snags	Point Density (µ ± sd)
Small (<40 cm)	Intact	35	13.2 ± 7
	Broken	48	11.2 ± 5
Large (≥40 cm)	Intact	44	12.4 ± 5
	Broken	77	12.4 ± 7

).

The thirteen lidar-derived metrics (Table 2) were used as predictor variables for classification into one of the four snag classes (SI, SB, LI, or LB). The number of RF trees to grow was set to 1000, and the number of predictor variables performing data partitioning at each node (mtry) was set to 13. Pearson’s correlation (r) was used to determine whether any predictor variables were highly correlated (r > 0.9; see Appendix A

Table A2. Pearson’s correlations among predictor variables. A correlation table showing all pairwise Pearson’s (r) correlation scores across the 13 predictor variables used for modeling snag classifications. A list of the predictor variable descriptions can be found in Table 2. Scores with an absolute value of r ≥ 0.9 were considered “strongly correlated” and are highlighted in grey. Positive scores suggest a relationship where a pair changes value in the same direction, while negative scores indicate a relationship where a pair changes value in opposite directions.

	PTDEN	P1stRN	P2ndRN	P3rdRN	GFPmid	LADcv	RUMPLE	ENTmid	VAI	VCI	ELEV	TRASP	SLOPE
PTDEN		−0.34	0.34	0.24	−0.14	0.04	−0.01	0.25	0.40	0.45	−0.33	0.02	−0.03
P1stRN	−0.34		−0.97	−0.83	0.02	−0.16	−0.10	−0.45	−0.30	−0.66	0.13	0.17	0.07
P2ndRN	0.34	−0.97		0.68	−0.05	0.15	0.11	0.39	0.32	0.62	−0.21	−0.13	−0.09
P3rdRN	0.24	−0.83	0.68		0.05	0.15	0.05	0.48	0.17	0.56	0.07	−0.22	0.02
GFPmid	−0.14	0.02	−0.05	0.05		−0.32	0.33	0.35	−0.47	−0.01	0.11	−0.12	−0.02
LADcv	0.04	−0.16	0.15	0.15	−0.32		−0.42	0.07	0.20	0.21	0.07	0.00	0.06
RUMPLE	−0.01	−0.10	0.11	0.05	0.33	−0.42		0.15	−0.30	0.28	−0.03	−0.05	−0.04
ENTmid	0.25	−0.45	0.39	0.48	0.35	0.07	0.15		−0.02	0.54	0.04	−0.26	0.00
VAI	0.40	−0.30	0.32	0.17	−0.47	0.20	−0.30	−0.02		0.30	−0.12	0.04	−0.14
VCI	0.45	−0.66	0.62	0.56	−0.01	0.21	0.28	0.54	0.30		−0.13	−0.18	−0.07
ELEV	−0.33	0.13	−0.21	0.07	0.11	0.07	−0.03	0.04	−0.12	−0.13		−0.13	0.18
TRASP	0.02	0.17	−0.13	−0.22	−0.12	0.00	−0.05	−0.26	0.04	−0.18	−0.13		−0.44
SLOPE	−0.03	0.07	−0.09	0.02	−0.02	0.06	−0.04	0.00	−0.14	−0.07	0.18	−0.44

). As there was a high correlation found between p1stRN and p2ndRN (r = 0.97), a multicollinearity test was performed, and no predictors were found to be collinear. As this study was conducted to investigate how return number metrics interact with snags, we kept both P1stRn and P2ndRN as predictor variables in our RF models. We would recommend that analysis using multivariate models other than RF (e.g., regression) should exclude P1stRN as a variable, as such models may be less resistant to multicollinearity.

For validation purposes, RF models were run within a bootstrap with 20 iterations. For each iteration, we drew 60% of the snags (n_train = 118) from the total available snag population (n_total = 198) to train the RF model. The remaining snags not drawn per iteration (n_test = 80) were used for independent validation of the RF model. For each bootstrap iteration, confusion matrices of observed versus predicted classifications were used to calculate overall accuracy and the kappa statistic (a coefficient ranging from 0 to 1, where 0 is equated with random chance and 1 is perfect concordance) [44], as well as producer’s accuracy (inverse of omission error) and user’s accuracy (inverse of commission error) for each class.

In addition to the confusion matrix, an evaluation of predictor variable importance was reported for the top RF model (RF_ALL) in terms of mean decrease in the Gini Index (a measure of the decrease in node impurity) [41,45]. To evaluate the importance of each predictor relative to one another among the four snag classes (and across models), the class-specific variable importance scores were standardized using the Model Improvement Ration (MIR) [46], whereby all raw variable importance scores were divided by the maximum.

2.6. Modeling Subset by Diameter

We conducted additional RF modeling on subsets of the snags by diameter, modeling only small snags (n_total = 82) and only large snags (n_total = 116) against the same suite of predictor variables and using the same RF parameters and validation methods. The only change was that classification was reduced from the four snag classes to only two based on snag intactness (intact versus broken top) for each model. The confusion matrix and predictor variable importance tables for the top RF models (small snags = RF_SM; large snags = RF_LG) let us further evaluate which of the 13 variables were most important for each size class.

3. Results

3.1. Model Performance across All Four Snag Classes

Across the 20 iterations of RF models classifying all snags into four classes by diameter and intactness, the top model (RF_ALL) had an overall accuracy of 50%, with a kappa statistic of 0.29 (

Table 4. Confusion matrices from the top random forest models for classifying snags within conifer forests in Idaho, USA. RF classification used ALS lidar metrics to split snags into groups across known characteristics. There were three RF models used across the full dataset: (a) all snags (split into four classes: “small intact” (SI), “small broken” (SB), “large intact” (LI), and “large broken” (LB); n_train = 118, n_test = 80); (b) small-diameter snags only (using intactness as a binary class; n_train = 49, n_test = 33); and (c) large-diameter snags only (using intactness as a binary class; n_train = 69, n_test = 47). In each table, the matrix on the left shows the number of correct and incorrect classifications per snag class; correct classifications are those where the predicted matched the observed snag class, highlighted in grey on the diagonal. On the right, the accuracy metrics per class are shown in grey: producer’s accuracy (correct/observed sum) and user’s accuracy (correct/predicted sum). Overall accuracy and the kappa statistic are listed in the bottom-left corner of each table, below which are the top three predictor variables for the model (ranked by mean decrease in Gini).

(a) All Snags
		Observed
	Class	SI	SB	LI	LB	Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
Predicted	SI	6	1	1	0	8	35.3	75.0
	SB	7	8	3	2	20	50.0	40.0
	LI	1	1	3	5	10	17.7	30.0
	LB	3	6	10	23	42	76.7	54.8
	Sum	17	16	17	30	80
Overall accuracy = 50%; kappa = 0.29
Top predictor variables: P3rdRN, LADcv, ELEV
(b) Small Snags Only
		Observed
	Class	Intact		Broken		Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
Predicted	Intact	17		3		20	77.3	85.0
	Broken	5		8		13	72.7	61.5
	Sum	22		11		33
Overall accuracy = 76%; kappa = 0.49
Top predictor variables: LADcv, PTDEN, ENTmid
(c) Large Snags Only
		Observed
	Class	Intact		Broken		Sum	Producer’s Accuracy (%)	User’s Accuracy (%)
Predicted	Intact	27		9		36	93.1	75.0
	Broken	2		9		11	50.0	81.8
	Sum	29		18		47
Overall accuracy = 77%; kappa = 0.47
Top predictor variables: LADcv, ENTmid, P3rdRN

a). Performance accuracies were highly variable by snag class, with large broken top snags having the highest producer’s accuracy, small intact snags having the highest user’s accuracy, and large intact snags having the lowest accuracy for both (Table 4a). The most important overall predictor variables for RF_ALL (based on mean decrease in Gini) were percent of third returns (P3rdRN), coefficient of variation in Leaf Area Density (LADcv), elevation (ELEV), and Vegetation Area Index (VAI;

Table 5. Predictor variable importance from the top random forest models for classifying snags within conifer forests in Idaho, USA. There were three RF models used across the full dataset: (a) all snags (with four classes: “small intact” (SI), “small broken” (SB), “large intact” (LI), and “large broken” (LB)); (b) small-diameter snags only (using intactness as a binary class); and (c) large-diameter snags only (using intactness as a binary class). For the class-specific columns, all scores for each class were adjusted via MIR, where each value was divided by the largest absolute value as a means of standardization across models [46]. The mean decrease in Gini (MDGini) refers to the total decrease in node impurities from splitting on that variable averaged over all RF trees [41]. All rows are sorted by MDGini (indicated by the small down arrow), as this was used to rank predictor variables in terms of overall variable importance.

(a) All Snags
Variable	SI	SB	LI	LB	MDGini ↓
P3rdRN	−0.53	0.25	−0.13	1.00	9.513
LADcv	0.06	−0.41	−0.21	0.36	8.105
ELEV	0.46	0.43	0.07	−0.11	7.636
VAI	0.01	−0.21	0.51	−0.07	7.445
VCI	−0.25	−0.04	−0.08	0.47	7.365
ENTmid	−0.24	−0.34	0.18	0.14	7.113
RUMPLE	0.00	0.07	0.01	−0.27	6.804
GFPmid	0.03	−0.24	−0.09	−0.10	6.022
SLOPE	0.28	0.30	0.00	0.09	5.964
PTDEN	−0.44	−0.35	−0.26	0.10	5.827
P1stRN	−0.28	−0.10	0.05	0.17	4.900
P2ndRN	−0.17	−0.26	−0.24	0.35	4.536
TRASP	−0.22	−0.42	0.17	−0.06	4.028
(b) Small Snags Only
Variable	Intact	Broken			MDGini ↓
LADcv	0.94	0.39			3.60
PTDEN	0.98	0.64			3.12
ENTmid	−0.99	−0.34			2.41
GFPmid	−0.52	−1.00			2.29
ELEV	0.72	−0.11			1.90
SLOPE	−0.14	−0.51			1.81
P1stRN	0.04	−0.15			1.78
P3rdRN	−0.42	−0.04			1.57
VAI	0.37	−0.38			1.56
TRASP	−0.51	−0.06			1.19
VCI	−0.57	−0.47			1.04
RUMPLE	−0.97	−0.44			0.94
P2ndRN	−0.93	−0.47			0.82
(c) Large Snags Only
Variable	Intact	Broken			MDGini ↓
LADcv	−0.61	0.02			5.34
ENTmid	−0.31	0.01			3.43
P3rdRN	−0.64	0.27			2.90
PTDEN	−0.45	−0.01			2.37
ELEV	−0.32	−0.23			2.25
RUMPLE	−0.47	0.22			2.19
VCI	−0.69	−0.10			2.15
GFPmid	−1.00	−0.48			2.15
VAI	−0.72	−0.38			2.01
TRASP	−0.35	−0.15			1.97
SLOPE	−0.27	0.37			1.89
P2ndRN	−0.55	0.18			1.47
P1stRN	−0.66	0.29			1.16

a). Three of these top variables were the most important predictors for the individual snag classes (Table 5a). The most important variable for both small intact and small broken snags was ELEV; for large intact snags it was VAI, and for large broken snags it was P3rdRN. LADcv was distinct from the other top variables in not being the most important for any given snag class (Table 5a).

3.2. Model Performance Subset by Diameter

When snags were subset by diameter, RF model performance improved for each subset as compared to the top model for all snags (Table 4). For small snags only, across the 20 iterations of RF models classifying snags into two groups by intactness, the overall accuracy of the top model (RF_SM) increased by 26% over RF_ALL. The confusion matrix for RF_SM (Table 4b) showed much higher performance accuracies across both classes. Out of the top three overall predictor variables from RF_ALL, only LADcv remained in the top three overall for RF_SM (Table 5b).

For large snags only, across the 20 iterations of RF models classifying snags into two groups by intactness, the overall accuracy of the top model (RF_LG) increased by 27% over RF_ALL. The confusion matrix for RF_LG showed improved performance accuracies across each class except for (large) broken snags; producer’s accuracy had the lowest value of the snag subsets (50% for broken tops), but also the highest value (93% for intact tops; Table 4c). Out of the top three overall predictor variables from RF_ALL, once again LADcv remained in the top three overall for RF_LG, as well as P3rdRN (Table 5c).

4. Discussion

Advancing our understanding of where broken-top snags occur within a closed-canopy forest has the potential to benefit habitat management for multiple wildlife species. Our goal was to explore whether ALS data could be used to differentiate tree top intactness of snags with known structural characteristics of value to wildlife. To our knowledge, this was the first study to use ALS data to focus on structural differences among snags, particularly in closed-canopy conifer forests.

The accuracy of our overall RF model for classifying snags by diameter and intactness was relatively low, suggesting there may not have been clear enough distinctions among the four snag classes to accurately distinguish all of them at the individual tree level with airborne lidar alone. Inclusion of additional information provided by other sensors, such as very-high-resolution satellite or airborne (including unmanned aircraft systems or UAS) imagery, could improve discrimination capability. Adjusting the modeling strategy also has potential for improvement. When our models were subset by diameter to examine intactness among only small snags and only large snags separately, the overall model accuracies and kappa statistics both improved to above 75% and 0.45, respectively. These findings suggested there is potential for improved applications given further refinement, especially when focused more narrowly on one or two snag classes.

One factor that is important to consider with ALS applications relative to snag detection and characterization of snag characteristics is the ALS point density. Higher point densities are generally associated with high levels of accuracy. For instance, Krzystek et al. [33] were able to characterize snags via lidar metrics and 3D shape from an ALS dataset with excellent accuracy (>90%), but with a much greater point density (55 points/m²) than available for our study. The snags studied by Krzystek et al. were primarily pest-infected, and thus had accumulated in larger groups [33], which represented a much different context than our study of using ALS to classify individual snags across a closed-canopy forest. Other studies also had relatively high accuracies associated with ALS applications of snags with relatively high point densities [24,29].

In order to place our point densities within a broader standardized framework, we used the Topographic Data Quality Levels (QLs) as defined by the United States Geological Survey (USGS) 3D Elevation Program [47] to evaluate the quality of our ALS datasets. We focused on three QLs (based on points per meter squared): QL1 (≥8), QL2 (2–7.9), and QL3 (0.5–1.9). The overall point density across both sitewide lidar acquisitions in our study was 4.2 points/m² (placing it within the QL2 category), but point densities of individual snags varied a great deal, and spanned all three QLs. Even within the same survey plot, point densities could be highly variable. For example, one plot with 12 snags had point densities that ranged from 1.7 to 20.4 points/m², spanning all three QLs (Figure 3). We found the lower limit of point densities required to properly calculate the lidar metrics of interest around individual snags was 1 point/m².

There were no strong drivers affecting point densities universally, though elevation did show weak negative associations (higher elevations had lower point densities across sites). Two additional factors that likely contributed to variable QLs around individual snags were scan angle and surrounding live crown proximity. Scan angle showed no strong relationship with point density but may still have played important albeit disparate roles in reflecting snag returns: returns close to nadir may have better reflected the tops of snags surrounded by dense taller canopies and differentiated them from a true gap, while shallower view pulse angles were more likely to reflect a greater number of returns from snag boles, especially at the edge of gaps. Surrounding live crown proximity likely affected QLs as well; live tree canopy returns within the 5 m diameter point cloud around a given snag would be counted toward snag point density, falsely raising QL. This is an expected challenge when looking for lone snags in a dense closed-canopy forest; many of the snags we surveyed were found at the edge of a gap, with some partially or almost completely underneath surrounding live canopy, especially broken-top snags. All of these factors combined suggested that the relatively low point densities in our ALS data likely contributed to a limited ability to classify tree intactness when small snags were included in the data sets.

Our finding that larger DBH snags were identified with higher classification accuracies was consistent with previous snag-detection work. Prior work in mapping snag presence or absence has shown DBH to be a strong predictor of snag-detection probability [14,28], where the likelihood of detecting snags increased with diameter. Our results were consistent with these findings, even though we were investigating the ability of ALS to classify snag characteristics, as opposed to detecting snags.

It is important to note that the ecological context of remote-sensing studies focused on snag detection can vary widely. Much of the previous work in mapping snags has been carried out where one type of massive tree die-off event has occurred, such as a wildfire or beetle kill/outbreak [24,26,27,29,33]. While such results certainly provide opportunities to evaluate the power of remote sensing to address snag-related questions of distribution and biomass, the structural characteristics of the snags themselves have not typically been the focus of wildlife-related investigations, although the role of these snags for wildlife use has been well documented [48,49].

Of particular interest to us, though, are individual snags that are embedded within dense live conifer forests that provide a valuable resource for many wildlife species. Our focus on the structural characteristics of broken versus intact tops of snags has important relevance for many wildlife species of management interest. For instance, the federally listed northern spotted owl (Strix occidentalis caurina) [50] uses snags as platforms for nesting, as do multiple other species of management interest, such as the Northern goshawk and great gray owl [12,13,35,51]. These species also require forests with high canopy closure for foraging and protection from predators [11,12,13,50]. Further, the importance of broken tops for wildlife is not limited to direct nesting or roosting use; broken tops also serve as an indicator of additional use by wildlife, particularly in the form of woodpecker cavity excavation [52]. Nests excavated by woodpeckers (primarily in snags) can support entire networks of cavity-reliant bird and mammal species within conifer-dominated forests [53,54,55], lending added importance to the value of identifying broken-top snags amongst closed-canopy forests for wildlife management efforts.

This individual tree approach was meant as a case study to better inform workflows at broader extents. We sought to improve parameterization for individual structural elements, in order to improve upon search patterns applied across entire landscapes. Viewing these results as one step within a broader stepwise approach for forest characterization via ALS-derived lidar metrics lends greater weight to our findings. A prerequisite first step could be to refine RF modeling at the plot or stand level to differentiate live trees from snags (e.g., [29]) prior to RF modeling at the individual tree level, to evaluate within-group differences among live tree and snag characteristics separately. While our study was novel in attempting to differentiate structural differences among snags, there is a great deal of value in looking at how this methodology compares to and can be combined with pre-existing methods in snag modeling (e.g., via intensity and height-based metrics [14,26,28,29,33]).

Going forward, we would suggest that those wishing to apply some aspect of these methods do the following to yield better results: focus on metrics for one class at a time (e.g., large broken-top snags only), and raise the height cutoff to 5 or 10 m above ground. Additionally, if calibrated ALS intensity data (or very-high-resolution imagery) are available, it would certainly be worth incorporating, either into RF models or for other methods of snag characterization. Further, higher-density point clouds (QL1) would undoubtedly improve model performance, and likely better distinguish among groups. Thankfully, the structural features of snags on which we focused (based on benefit to wildlife) were positively correlated with characterization via ALS, which suggested there is value in focusing more closely on just those snag classes that hold the greatest benefits for wildlife: larger-diameter snags, as well as broken-top snags [2,15,51]. By limiting the focus of snag detection or modeling efforts to the binary of presence/absence for large broken snags only, the focus can shift to lidar (or spectral) metrics most strongly correlated with this class (e.g., LADcv, ENTmid, and P3rdRN).

5. Conclusions

While we used ALS alone in this study, the next step would be to focus on multisensor or data-fusion approaches (such as incorporating multi- or hyperspectral lidar data, satellite imagery, and/or photogrammetry), which could lead to far more robust predictions resulting from a greater diversity of spatial, spectral, and temporal resolutions that add complementary dimensions of information [28,29,56]. Employing modeling methods other than RF (such as imputation [57], gradient boosting [58], or artificial neural networks [59]) may also lead to improved results and uncover useful predictors of forest structures not previously applied. As open-access data sets continue to be more widely accessible, the concepts discussed become more readily applicable; applying novel methods to broader swaths of data becomes more feasible, incorporating multiple sources of data becomes easier, and comparisons of competing methodologies can be tested more rigorously. We encourage continued investigation of ways in which new and upcoming tools can be used to better characterize forest structures remotely, across a variety of landscapes, especially with respect to snags and other wildlife habitat features.