Learning Pairwise Potential CRFs in Deep Siamese Network for Change Detection
Abstract
:1. Introduction
- (1)
- We propose a novel deep Siamese pairwise potential CRFs network (PPNet) for change detection, which uses an end-to-end training method. We introduce CRF-RNN module which integrates the knowledge of unary potential and pairwise potential in the end-to-end training and improves the overall performance of the whole algorithm. To the author’s knowledge, this method is the first to implement end-to-end FCCRF convolutional neural network in change detection;
- (2)
- In order to correct the identification errors of front-end network, this method uses ECA to further distinguish the changed area effectively. ECA uses one-dimension convolution with adaptive kernel size to avoid dimension reductions and maintain the appropriate crosschannel interactions. This method is the first to verify the effectiveness of ECA in the application of change detection;
- (3)
- Our experimental results on two data sets verify that this method has advanced capability in the same kind of methods. This method improves the capability of change detection without increasing the number of parameters and avoids the overfitting phenomenon in the training process.
2. Methodology
2.1. CRF-RNN Unit
2.2. ECA Unit
2.3. VHR Images Change Detection Algorithm Based on PPNet
2.4. End-to-End Training
3. Results
3.1. Data Sets
3.2. Experimental Details
3.2.1. Evaluation Indexes
3.2.2. Parameter Settings
3.3. Comparison Results
3.4. Failure Cases
4. Discussions
4.1. Ablation Study
4.2. Parameters Selection in CRF-RNN Unit
4.3. Comparative Study with SE Attention
4.4. Comparison of the Total Number of Network Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xian, G.; Homer, C.; Fry, J. Updating the 2001 National Land Cover Database land cover classification to 2006 by using Landsat imagery change detection methods. Remote Sens. Environ. 2009, 113, 1133–1147. [Google Scholar] [CrossRef] [Green Version]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Review ArticleDigital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Luo, H.; Liu, C.; Wu, C.; Guo, X. Urban Change Detection Based on Dempster–Shafer Theory for Multitemporal Very High-Resolution Imagery. Remote Sens. 2018, 10, 980. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake Damage Assessment of Buildings Using VHR Optical and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef] [Green Version]
- Zelinski, M.E.; Henderson, J.; Smith, M. Use of Landsat 5 for Change Detection at 1998 Indian and Pakistani Nuclear Test Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3453–3460. [Google Scholar] [CrossRef]
- Singh, A. Review Article Digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wu, C. Advance and Future Development of Change Detection for Multi-temporal Remote Sensing Imagery. Acta Geod. Cartogr. Sin. 2017, 46, 1447. [Google Scholar]
- Ridd, M.K.; Liu, J. A Comparison of Four Algorithms for Change Detection in an Urban Environment. Remote Sens. Environ. 1998, 63, 95–100. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, M.; Zhang, P.; Su, L.; Shi, J. Feature-Level Change Detection Using Deep Representation and Feature Change Analysis for Multispectral Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1666–1670. [Google Scholar] [CrossRef]
- Zhuang, H.; Deng, K.; Fan, H.; Yu, M. Strategies Combining Spectral Angle Mapper and Change Vector Analysis to Unsupervised Change Detection in Multispectral Images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 681–685. [Google Scholar] [CrossRef]
- Malila, W.A. Change Vector Analysis: An Approach for Detecting Forest Changes with Landsat. LARS Symp. 1980, 385–397. Available online: https://docs.lib.purdue.edu/lars_symp/385/ (accessed on 22 December 2021).
- Bovolo, F.; Marchesi, S.; Bruzzone, L. A Framework for Automatic and Unsupervised Detection of Multiple Changes in Multitemporal Images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2196–2212. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A Theoretical Framework for Unsupervised Change Detection Based on Change Vector Analysis in the Polar Domain. IEEE Trans. Geosci. Remote Sens. 2007, 45, 218–236. [Google Scholar] [CrossRef] [Green Version]
- Bovolo, F.; Bruzzone, L. An adaptive thresholding approach to multiple-change detection in multispectral images. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 233–236. [Google Scholar]
- Baisantry, M.; Negi, D.S.; Manocha, O.P. Change Vector Analysis using Enhanced PCA and Inverse Triangular Function-based Thresholding. Def. Sci. J. 2012, 62, 236–242. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate Alteration Detection (MAD) and MAF Postprocessing in Multispectral, Bitemporal Image Data: New Approaches to Change Detection Studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, A.A. The Regularized Iteratively Reweighted MAD Method for Change Detection in Multi- and Hyperspectral Data. IEEE Trans. Image Process. 2007, 16, 463–478. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Zhang, L.; Du, B. Kernel Slow Feature Analysis for Scene Change Detection. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2367–2384. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L.; Huang, X. Object-oriented change detection based on the Kolmogorov–Smirnov test using high-resolution multispectral imagery. Int. J. Remote Sens. 2011, 32, 5719–5740. [Google Scholar] [CrossRef]
- Wen, D.; Huang, X.; Zhang, L.; Benediktsson, J.A. A Novel Automatic Change Detection Method for Urban High-Resolution Remotely Sensed Imagery Based on Multiindex Scene Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 609–625. [Google Scholar] [CrossRef]
- Tan, K.; Jin, X.; Plaza, A.; Wang, X.; Xiao, L.; Du, P. Automatic Change Detection in High-Resolution Remote Sensing Images by Using a Multiple Classifier System and Spectral–Spatial Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3439–3451. [Google Scholar] [CrossRef]
- Huo, C.; Zhou, Z.; Lu, H.; Pan, C.; Chen, K. Fast Object-Level Change Detection for VHR Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 118–122. [Google Scholar] [CrossRef]
- Lei, Z.; Fang, T.; Huo, H.; Li, D. Bi-Temporal Texton Forest for Land Cover Transition Detection on Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1227–1237. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Chen, G.; Hay, G.J.; Carvalho, L.M.T.; Wulder, M.A. Object-based change detection. Int. J. Remote Sens. 2012, 33, 4434–4457. [Google Scholar] [CrossRef]
- Benedek, C.; Sziranyi, T. Change Detection in Optical Aerial Images by a Multilayer Conditional Mixed Markov Model. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3416–3430. [Google Scholar] [CrossRef] [Green Version]
- Moser, G.; Angiati, E.; Serpico, S.B. Multiscale Unsupervised Change Detection on Optical Images by Markov Random Fields and Wavelets. IEEE Geosci. Remote Sens. Lett. 2011, 8, 725–729. [Google Scholar] [CrossRef]
- Hoberg, T.; Rottensteiner, F.; Feitosa, R.Q.; Heipke, C. Conditional Random Fields for Multitemporal and Multiscale Classification of Optical Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 659–673. [Google Scholar] [CrossRef]
- Zhou, L.; Cao, G.; Li, Y.; Shang, Y. Change Detection Based on Conditional Random Field With Region Connection Constraints in High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3478–3488. [Google Scholar] [CrossRef]
- Lv, P.; Zhong, Y.; Zhao, J.; Zhang, L. Unsupervised Change Detection Based on Hybrid Conditional Random Field Model for High Spatial Resolution Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4002–4015. [Google Scholar] [CrossRef]
- Sutton, C.; Mccallum, A. An Introduction to Conditional Random Fields. Found. Trends Mach. Learn. 2010, 4, 267–373. [Google Scholar] [CrossRef]
- Li, S.Z. Markov random field models in computer vision. In Computer Vision—ECCV ’94; Eklundh, J.O., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 361–370. [Google Scholar]
- Liu, F.; Lin, G.; Shen, C. CRF Learning with CNN Features for Image Segmentation. Pattern Recognit. 2015, 48, 2983–2992. [Google Scholar] [CrossRef] [Green Version]
- Paisitkriangkrai, S.; Sherrah, J.; Janney, P.; Hengel, V.D. Effective semantic pixel labelling with convolutional networks and Conditional Random Fields. In Proceedings of the Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G. Deep Convolutional Neural Fields for Depth Estimation from a Single Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Bell, S.; Upchurch, P.; Snavely, N.; Bala, K. Material Recognition in the Wild with the Materials in Context Database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Bovolo, F.; Bruzzone, L. Unsupervised Deep Change Vector Analysis for Multiple-Change Detection in VHR Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3677–3693. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A Deep Convolutional Coupling Network for Change Detection Based on Heterogeneous Optical and Radar Images. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 545–559. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change Detection Based on Deep Siamese Convolutional Network for Optical Aerial Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Caye Daudt, R.; Le Saux, B.; Boulch, A. Fully Convolutional Siamese Networks for Change Detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar]
- Chen, H.; Wu, C.; Du, B.; Zhang, L. Deep Siamese Multi-scale Convolutional Network for Change Detection in Multi-temporal VHR Images. In Proceedings of the 2019 10th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp), Shanghai, China, 5–7 August 2019; pp. 1–4. [Google Scholar]
- Krhenbühl, P.; Koltun, V. Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Granada, Spain, 12–17 December 2011; Volume 24. [Google Scholar]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P.H.S. Conditional Random Fields as Recurrent Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, Y.; Kalantidis, Y.; Li, J.; Yan, S.; Feng, J. A2-Nets: Double Attention Networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montréal, QC, Canada, 2–8 December 2018; Volume 31. [Google Scholar]
- Gao, Z.; Xie, J.; Wang, Q.; Li, P. Global Second-Order Pooling Convolutional Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Rooker, T. Review of Neurocomputing: Foundations of Research. AI Mag. 1989, 10, 64. [Google Scholar]
- Mozer, M.C. A Focused Backpropagation Algorithm for Temporal. In Backpropagation: Theory, Architectures, and Applications; Psychology Press: Hove, UK, 1995; pp. 137–170. [Google Scholar]
- Zhang, T.; Qi, G.J.; Xiao, B.; Wang, J. Interleaved Group Convolutions. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Xie, S.; Girshick, R.; Dollar, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ioannou, Y.; Robertson, D.; Cipolla, R.; Criminisi, A. Deep Roots: Improving CNN Efficiency With Hierarchical Filter Groups. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Huo, C.; Chen, K.; Ding, K.; Zhou, Z.; Pan, C. Learning Relationship for Very High Resolution Image Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3384–3394. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, G.; Chen, K.; Yan, M.; Sun, X. Triplet-Based Semantic Relation Learning for Aerial Remote Sensing Image Change Detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 266–270. [Google Scholar] [CrossRef]
- Chen, H.; Shi, Z. A Spatial-Temporal Attention-Based Method and a New Dataset for Remote Sensing Image Change Detection. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Liu, Y.; Pang, C.; Zhan, Z.; Zhang, X.; Yang, X. Building Change Detection for Remote Sensing Images Using a Dual-Task Constrained Deep Siamese Convolutional Network Model. IEEE Geosci. Remote Sens. Lett. 2020, 18, 811–815. [Google Scholar] [CrossRef]
- Cz, A.; Peng, Y.; Dt, E.; Lj, B.; Bs, B.; Li, H.B.; Gl, B. A deeply supervised image fusion network for change detection in high resolution bi-temporal remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 166, 183–200. [Google Scholar]
- Fang, S.; Li, K.; Shao, J.; Li, Z. SNUNet-CD: A Densely Connected Siamese Network for Change Detection of VHR Images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, H.; Qi, Z.; Shi, Z. Remote Sensing Image Change Detection with Transformers. IEEE Trans. Geosci. Remote Sens. 2021, 5607514. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]










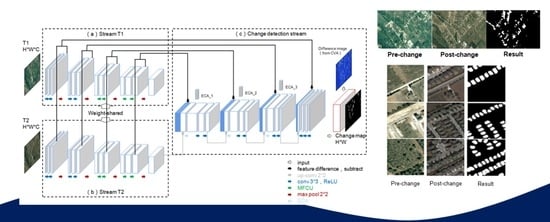
| The VHR images change detection algorithm based on PPNet. |
|---|
| Input: |
| 1. A pair of VHR images in the same region at different times with a corresponding ground truth. |
| Step 1: Pairwise VHR images are clipped according to the corresponding size, and then the whole Images T1 and T2 of pairwise H × W × C are put into the network. |
| Step 2: The training is carried out on the training set or verification set by the DSMS-FCN network joining ECA. The deep features and deep difference features of paired images were extracted from the same feature space of Stream T1 and Stream T2, and then change detection stream was used to discriminate the changed regions. The relatively rough change probability image U is obtained. |
| Step 3: CVA is used to calculate the differential image of pairwise VHR images. |
| Step 4: The change probability image U and the difference image are taken as the input of CRF-RNN unit, and the network weight obtained in step 2 is taken as the initial value, which conduct joint training with pairwise potential CRF-RNN on the training set or verification set. The number of iterations T in CRF-RNN is generally set to 5. Finally, the optimal network weight of PPNet can be obtained. |
| Step 5: By inputting pairwise test images, the end-to-end network infers the change map of H × W and obtains the changed regions and the unchanged regions. |
| Output: |
| 1. Change map. |
| Method | Pre. | Rec. | F1 | OA |
|---|---|---|---|---|
| RL | 0.431 | 0.507 | 0.466 | NA |
| TBSRL | 0.444 | 0.619 | 0.517 | NA |
| DSCN | 0.412 | 0.574 | 0.479 | NA |
| CXM | 0.365 | 0.584 | 0.449 | NA |
| SCCN | 0.224 | 0.347 | 0.287 | NA |
| STANet | 0.455 | 0.635 | 0.530 | NA |
| FC-EF | 0.4729 | 0.4399 | 0.4558 | 0.9341 |
| FC-Siam-Conc | 0.4562 | 0.4808 | 0.4682 | 0.9395 |
| FC-Siam-Diff | 0.6053 | 0.4561 | 0.5202 | 0.9349 |
| DSMS-FCN | 0.6076 | 0.4833 | 0.5616 | 0.9430 |
| DSMS-FCN-FCCRF | 0.5684 | 0.5186 | 0.5423 | 0.9440 |
| DSMS-FCN-ECA(Ours) | 0.6640 | 0.5023 | 0.5719 | 0.9420 |
| PPNet(Ours) | 0.6736 | 0.4819 | 0.5619 | 0.9485 |
| Method | Pre. | Rec. | F1 | OA | Kappa |
|---|---|---|---|---|---|
| FC-EF | 0.8398 | 0.6723 | 0.7468 | 0.9768 | 0.7348 |
| FC-Siam-Conc | 0.9307 | 0.7559 | 0.8342 | 0.9847 | 0.8263 |
| FC-Siam-Diff | 0.9353 | 0.7374 | 0.8247 | 0.9840 | 0.8164 |
| DSMS-FCN | 0.9359 | 0.7342 | 0.8229 | 0.9839 | 0.8146 |
| DSMS-FCN-FCCRF | 0.9360 | 0.7344 | 0.8230 | 0.9839 | 0.8147 |
| DSMS-FCN-ECA(Ours) | 0.9277 | 0.7730 | 0.8433 | 0.9854 | 0.8357 |
| PPNet(Ours) | 0.9193 | 0.7919 | 0.8508 | 0.9859 | 0.8435 |
| Method | FCCRF | CRF-RNN | ECA | F1 | OA | Kappa |
|---|---|---|---|---|---|---|
| DSMS-FCN(base) | ✗ | ✗ | ✗ | 0.8354 | 0.9849 | 0.8276 |
| DSMS-FCN-FCCRF | ✓ | ✗ | ✗ | 0.8354 | 0.9849 | 0.8276 |
| DSMS-FCN-CRF-RNN | ✗ | ✓ | ✗ | 0.8399 | 0.9852 | 0.8324 |
| DSMS-FCN-ECA | ✗ | ✗ | ✓ | 0.8433 | 0.9854 | 0.8357 |
| PPNet | ✗ | ✓ | ✓ | 0.8508 | 0.9859 | 0.8435 |
| Method | F1 | OA | Kappa |
|---|---|---|---|
| DSMS-FCN-SE | 0.8400 | 0.9852 | 0.8324 |
| DSMS-FCN-ECA | 0.8433 | 0.9854 | 0.8357 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, D.; Wei, Z.; Wu, Z.; Liu, J. Learning Pairwise Potential CRFs in Deep Siamese Network for Change Detection. Remote Sens. 2022, 14, 841. https://doi.org/10.3390/rs14040841
Zheng D, Wei Z, Wu Z, Liu J. Learning Pairwise Potential CRFs in Deep Siamese Network for Change Detection. Remote Sensing. 2022; 14(4):841. https://doi.org/10.3390/rs14040841
Chicago/Turabian StyleZheng, Dalong, Zhihui Wei, Zebin Wu, and Jia Liu. 2022. "Learning Pairwise Potential CRFs in Deep Siamese Network for Change Detection" Remote Sensing 14, no. 4: 841. https://doi.org/10.3390/rs14040841
APA StyleZheng, D., Wei, Z., Wu, Z., & Liu, J. (2022). Learning Pairwise Potential CRFs in Deep Siamese Network for Change Detection. Remote Sensing, 14(4), 841. https://doi.org/10.3390/rs14040841