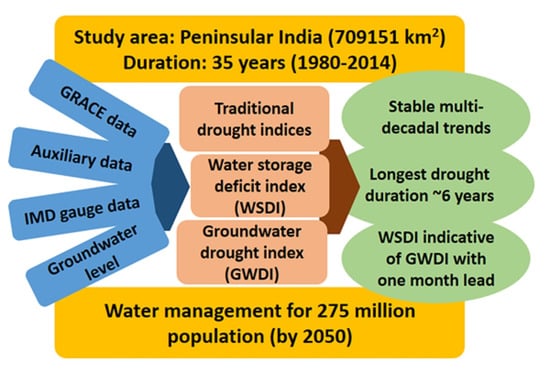
Multidecadal Land Water and Groundwater Drought Evaluation in Peninsular India
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Water Storage Components and Climate Data
2.3. Linear and Non-Linear Trend Analysis
2.4. Drought Severity and Recovery Time
2.5. Standardized Indices
3. Results and Discussion
3.1. Multidecadal Trends in WSCs
3.2. Estimation of Drought Severity and Recovery Time
3.3. How Well Does WSDI Compare with sc-PDSI and SPI12?
3.4. Characterizing GWDI and Potential of WSDI as a Proxy for GWDI
3.5. Inferences for the Sustainable Groundwater Utilities in the Study Region
3.6. Limitations of the Study
4. Conclusions
- The PCR-GLOBWB model is largely suitable for quantifying individual and integrated WSCs in a region and subsequent decadal droughts assessment for the period beyond GRACE records, especially prior to April 2002.
- Contrary to the near-surface storage components, the commonly invisible GWS showed a slow but persistent response (longest deficit period spanning ~6 years) to the seasonal variations of the hydrological fluxes and remained the major contributor to LWS.
- The observed behavior of occurrence of all of the severe-to-extreme drought events highlights the region’s vulnerability to drought conditions even in the monsoon season. This behavior, combined with the recovery time analysis, will help understand the temporal propagation of GW deficits and take precautionary measures to prevent overexploitation.
- WSDI holistically characterizes the drought intensity in a particular region owing to its independence from the geographical area. It enables us to quantify the integrated water deficit below average conditions, unlike the conventional indices where only a few hydrometeorological components are included, and therefore, it is useful in efficient drought monitoring.
- agrees favorably well (similar dynamics and high correlation (r = 0.53–0.70)) with the and , highlighting the potential of the remotely sensed WSDI as a quick proxy of groundwater with a lead time of one month, thus eliminating the need for the groundwater storage simulations in data-scarce river basins globally, which is otherwise quite complex and may inevitably possess high uncertainties.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Du, L.; Tian, Q.; Yu, T.; Meng, Q.; Jancsó, T.; Udvardy, P.; Huang, Y. A Comprehensive Drought Monitoring Method Integrating Modis and Trmm Data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J.; Liu, X. Drought Evaluation Using the Grace Terrestrial Water Storage Deficit over the Yangtze River Basin, China. Sci. Total Environ. 2018, 634, 727–738. [Google Scholar] [CrossRef] [PubMed]
- Jacobi, J.; Perrone, D.; Duncan, L.L.; Hornberger, G. A Tool for Calculating the Palmer Drought Indices. Water Resour. Res. 2013, 49, 6086–6089. [Google Scholar] [CrossRef]
- Abhishek; Kinouchi, T.; Sayama, T. A Comprehensive Assessment of Water Storage Dynamics and Hydroclimatic Extremes in the Chao Phraya River Basin during 2002–2020. J. Hydrol. 2021, 603, 126868. [Google Scholar] [CrossRef]
- Schreiner-Mcgraw, A.P.; Ajami, H. Delayed Response of Groundwater to Multi-Year Meteorological Droughts in the Absence of Anthropogenic Management. J. Hydrol. 2021, 603, 126917. [Google Scholar] [CrossRef]
- Dai, A. Increasing Drought under Global Warming in Observations and Models. Nat. Clim. Chang. 2013, 3, 52–58, Erratum in Nat. Clim. Chang. 2013, 3, 171. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Van Der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global Warming and Changes in Drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. Grace Groundwater Drought Index: Evaluation of California Central Valley Groundwater Drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P.; Bricker, S.H.; Morgan, R.B. Regional Analysis of Groundwater Droughts using Hydrograph Classification. Hydrol. Earth Syst. Sci. 2015, 19, 4327–4344. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; De Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global Grace Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; Mcguire, V.L.; Mcmahon, P.B. Groundwater Depletion and Sustainability of Irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; De Linage, C.R.; Rodell, M. Satellites Measure Recent Rates of Groundwater Depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.S. The Global Groundwater Crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.-H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying Renewable Groundwater Stress With Grace. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater Use for Irrigation—A Global Inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
- Zaveri, E.; Grogan, D.S.; Fisher-Vanden, K.; Frolking, S.; Lammers, R.B.; Wrenn, D.H.; Prusevich, A.; Nicholas, R.E. Invisible Water, Visible Impact: Groundwater Use and Indian Agriculture under Climate Change. Environ. Res. Lett. 2016, 11, 084005. [Google Scholar] [CrossRef] [Green Version]
- Worldbank India Groundwater: A Valuable but Diminishing Resource. Available online: http://www.worldbank.org/en/news/feature/2012/03/06/india-groundwater-critical-diminishing (accessed on 15 October 2021).
- Chindarkar, N.; Grafton, R.Q. India’s Depleting Groundwater: When Science Meets Policy. Asia Pac. Policy Stud. 2019, 6, 108–124. [Google Scholar] [CrossRef]
- CGWB. Dynamic Ground Water Dynamic Ground Water Resources of India; CGWB: New Delhi, India, 2014.
- Suhag, R. Overview Of Groundwater in India; Working Papers id:9504; eSocialSciences: Vashi, India, 2016. [Google Scholar]
- Li, B.; Rodell, M. Evaluation of a Model-Based Groundwater Drought Indicator in the Conterminous U.S. J. Hydrol. 2015, 526, 78–88. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.-H. Emerging Trends in Global Freshwater Availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; Van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global Models Underestimate Large Decadal Declining and Rising Water Storage Trends Relative to Grace Satellite Data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrew, R.; Guan, H.; Batelaan, O. Estimation of Grace Water Storage Components by Temporal Decomposition. J. Hydrol. 2017, 552, 341–350. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Zhao, X.; Yao, L.; Jiang, H.; Xu, J.; Yang, J.; Li, Y. Variations in Terrestrial Water Storage in the Lancang-Mekong River Basin from Grace Solutions and Land Surface Model. J. Hydrol. 2020, 580, 124258. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Rodell, M.; Seo, K.-W.; Wilson, C.; Scanlon, B.R.; Pokhrel, Y. Basin-Scale River Runoff Estimation from Grace Gravity Satellites, Climate Models, and In Situ Observations: A Case Study in the Amazon Basin. Water Resour. Res. 2020, 56, E2020wr028032. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Reedy, R.C.; Pool, D.R.; Save, H.; Long, D.; Chen, J.; Wolock, D.M.; Conway, B.D.; Winester, D. Hydrologic Implications of Grace Satellite Data in the Colorado River Basin. Water Resour. Res. 2015, 51, 9891–9903. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have Grace Satellites Overestimated Groundwater Depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef]
- Abhishek; Kinouchi, T. Synergetic Application of Grace Gravity Data, Global Hydrological Model, and In-Situ Observations to Quantify Water Storage Dynamics Over Peninsular India during 2002–2017. J. Hydrol. 2021, 596, 126069. [Google Scholar] [CrossRef]
- Kumar, K.S.; Rathnam, E.V.; Sridhar, V. Tracking seasonal and monthly drought with grace-based terrestrial water storage assessments over major river basins in South India. Sci. Total Environ. 2021, 763, 142994. [Google Scholar] [CrossRef]
- Goi Ground Water Year Book India 2016-Central Ground Water Board; Ministry of Water Resources; Government of India: Faridabad, India, 2017.
- Census of India. Report of The Technical Group on Population Projections. 2019. Available online: https://nhm.gov.in/New_Updates_2018/Report_Population_Projection_2019.pdf (accessed on 28 July 2021).
- CWC. Water and Related Statistics. Water Planning and Project Wing; Central Water Commission: New Delhi, India, 2020.
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over india and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Abhishek; Abolafia-Rosenzweig, R.; Kinouchi, T.; Ito, M. Water budget closure in the Upper Chao Phraya River basin, Thailand using multisource data. Remote Sens. 2022, 14, 173. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of grace time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Hodrick, R.J.; Prescott, E.C. Postwar U.S. Business Cycles: An Empirical Investigation. J. Money Crédit Bank. 1997, 29, 1–16. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A grace-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Trenberth, K.E.; Qian, T. A global dataset of palmer drought severity index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Hot Springs, AR, USA, 16–18 November 1983. [Google Scholar]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z. Spatiotemporal changes in China’s terrestrial water storage from grace satellites and its possible drivers. J. Geophys. Res. Atmos. 2019, 124, 11976–11993. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Mallya, G.; Mishra, V.; Niyogi, D.; Tripathi, S.; Govindaraju, R.S. Trends and variability of droughts over the indian monsoon region. Weather Clim. Extrem. 2016, 12, 43–68. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. estimating groundwater storage changes in the Mississippi river basin (USA) using grace. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Panda, D.K.; Wahr, J. Spatiotemporal Evolution of Water Storage Changes in India from the Updated Grace-Derived Gravity Records. Water Resour. Res. 2016, 52, 135–149. [Google Scholar] [CrossRef] [Green Version]
- Department of Water Resources; Mojs, J.S. Department of Water Resources, River Development & Ganga Rejuvenation, Government of India. Available online: http://jalshakti-dowr.gov.in/ (accessed on 28 August 2021).
- López, P.L.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of A large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef] [Green Version]
- Sutanudjaja, E.H.; Van Beek, L.P.H.; De Jong, S.M.; Van Geer, F.C.; Bierkens, M.F.P. Calibrating a large-extent high-resolution coupled groundwater-land surface model using soil moisture and discharge data. Water Resour. Res. 2014, 50, 687–705. [Google Scholar] [CrossRef]
- Richter, H.M.P.; Lück, C.; Klos, A.; Sideris, M.G.; Rangelova, E.; Kusche, J. Reconstructing grace-type time-variable gravity from the swarm satellites. Sci. Rep. 2021, 11, 1117. [Google Scholar] [CrossRef] [PubMed]






| River Basin | Geographical Area (km2) | Mean Annual Rainfall (mm) | Variability (Min.–Max.) in Rainfall (mm) | Estimated Population (Million) | Estimated Per Capita Water Availability (m3) | Current Category * | No. of Wells † | GWL Depth (m) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 2025 | 2050 | 2025 | 2050 | |||||||
| Godavari (GRB) | 312,812 | 1093 | 400–2500 | 89.18 | 104.92 | 1320.25 | 1122.19 | Water stressed | 430 | 33.6 |
| Krishna(KRB) | 254,750 | 859 | 100–4000 | 100.41 | 118.13 | 886.76 | 753.75 | Water scarce | 515 | 47.8 |
| Mahanadi (MRB) | 141,589 | 1292 | 1080–1653 | 43.93 | 51.68 | 1661.73 | 1412.54 | Water stressed | 135 | 34.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abhishek; Kinouchi, T. Multidecadal Land Water and Groundwater Drought Evaluation in Peninsular India. Remote Sens. 2022, 14, 1486. https://doi.org/10.3390/rs14061486
Abhishek, Kinouchi T. Multidecadal Land Water and Groundwater Drought Evaluation in Peninsular India. Remote Sensing. 2022; 14(6):1486. https://doi.org/10.3390/rs14061486
Chicago/Turabian StyleAbhishek, and Tsuyoshi Kinouchi. 2022. "Multidecadal Land Water and Groundwater Drought Evaluation in Peninsular India" Remote Sensing 14, no. 6: 1486. https://doi.org/10.3390/rs14061486
APA StyleAbhishek, & Kinouchi, T. (2022). Multidecadal Land Water and Groundwater Drought Evaluation in Peninsular India. Remote Sensing, 14(6), 1486. https://doi.org/10.3390/rs14061486