Classification of Tree Species in Different Seasons and Regions Based on Leaf Hyperspectral Images
Abstract
:1. Introduction
2. Materials and Methods
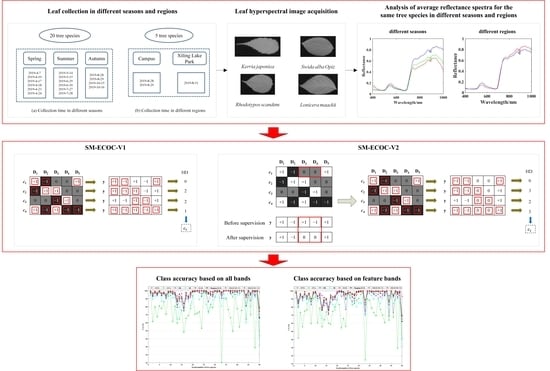
2.1. Experimental Materials
2.2. Hyperspectral Image Acquisition
2.3. Hyperspectral Data Extraction
3. Classification Models
3.1. Error-Correcting Output Codes
3.1.1. The Encoding Process
- (1)
- OVO: All classes are combined in pairs without repetition, in which one is treated as a positive class and the other is treated as a negative class. Therefore, a total of L = Nc(Nc − 1)/2 dichotomizers are trained, as shown in Figure 4a.
- (2)
- OVA: One of all classes is regarded as a positive class, and the remaining classes are regarded as a negative class. Therefore, a total of L = Nc dichotomizers are trained, as shown in Figure 4b.
- (3)
- DR: The elements in the coding matrix M generated by DR only contain +1 and −1, where +1 means positive class, −1 means negative class and both +1 and −1 are randomly generated with a probability of 0.5. In this way, a set of coding matrices is generated, and the coding matrix with the largest Hamming distance among all rows is selected to ensure the minimum correlation among the codes of each class, as shown in Figure 4c. It is suggested that L = 10logNc dichotomizers are created.
- (4)
- SR: The elements in the coding matrix M generated by SR contain +1, 0 and −1, where +1 means positive class, −1 means negative class and 0 means that the corresponding class does not participate in the training process of the dichotomizer. In this method, both +1 and −1 are randomly generated with a probability of 0.25, and 0 is generated with a probability of 0.5. A set of coding matrices is generated in this way. As with the DR method, the coding matrix with the largest Hamming distance among all rows is selected, as shown in Figure 4d. It is suggested that L = 15logNc dichotomizers are created.
3.1.2. The Decoding Process
3.2. Supervision Mechanism-Based ECOC
3.2.1. SM-ECOC-V1
3.2.2. SM-ECOC-V2
3.3. Selection of Base Classifier
4. Results and Discussion
4.1. Effects of Different Seasons and Regions on Spectral Response and Classification
4.1.1. Hyperspectral Response Analysis of Leaves in Different Seasons and Regions
4.1.2. Effects of Different Seasons and Regions on Tree Species Classification
4.2. Classification Performance Analysis of Supervision Mechanism-Based ECOC
4.2.1. Parameter Optimization
4.2.2. Classification of Tree Species Based on All Bands
4.2.3. Classification of Tree Species Based on Feature Bands
5. Conclusions
- Seasonal and regional changes have an effect on the reflectance spectra of tree species, especially in the near-infrared region of 760–1000 nm. When the spectral information of different seasons and different regions is added into the model, the tree species can be effectively classified.
- The proposed SM-ECOC-V1 and SM-ECOC-V2 methods outperform the ECOC method under SR coding strategy, which indicates that the supervision function of SM-ECOC-V1 and SM-ECOC-V2 methods can effectively avoid the influence of 0-element in SR coding matrix on classification performance.
- The proposed SM-ECOC-V2 method achieves the best classification performance based on both all bands and feature bands, which indicates that it plays an important role in improving the classification performance of the SR coding strategy that the SM-ECOC-V2 method utilizes Bagging-ELM multiclass classifiers to supervise the output results of the dichotomizers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.S.; Zhang, X.L. Research advances and countermeasures of remote sensing classification of forest vegetation. For. Resour. Manag. 2004, 1, 61–64. [Google Scholar] [CrossRef]
- Zeng, Q.W.; Wu, H.G. Development of hyperspectral remote sensing application in forest species identification. For. Resour. Manag. 2009, 109–114. [Google Scholar] [CrossRef]
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.W.; Hyyppa, J.; Saari, H.; Polonen, I.; Imai, N.N.; et al. Individual tree detection and classification with UAV-based photogrammetric point clouds and hyperspectral imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.M.; Mu, T.K.; Yan, T.Y.; Chen, Z.Y. Overview of hyperspectral remote sensing technology. Spacecr. Recovery Remote Sens. 2018, 39, 104–114. [Google Scholar]
- Zhao, C.Y.; Yang, Z.G. Technology of hyperspectral remote sensing (HRS) and its application to forest resources monitoring. For. Invent. Plan. 2006, 31, 4–6. [Google Scholar]
- Awad, M.M. Forest mapping: A comparison between hyperspectral and multispectral images and technologies. J. For. Res. 2018, 29, 1395–1405. [Google Scholar] [CrossRef]
- Mondal, B.; Saha, A.K.; Roy, A. Mapping mangroves using LISS-IV and Hyperion data in part of the Indian Sundarban. Int. J. Remote Sens. 2019, 40, 9380–9400. [Google Scholar] [CrossRef]
- Papes, M.; Tupayachi, R.; Martinez, P.; Peterson, A.T.; Asner, G.P.; Powell, G.V.N. Seasonal variation in spectral signatures of five genera of rainforest trees. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 339–350. [Google Scholar] [CrossRef]
- Wang, L.; Fan, W.Y. Hyperspectral remote sensing data for identifying dominant forest tree species group. J. Northeast. For. Univ. 2015, 43, 134–137. [Google Scholar]
- Zhang, Y.N. Application of remote sensing technology in forestry. Inner Mong. For. Investig. Des. 2017, 40, 86–87. [Google Scholar]
- Lucas, R.; Bunting, P.; Paterson, M.; Chisholm, L. Classification of Australian forest communities using aerial photography, CASI and HyMap data. Remote Sens. Environ. 2008, 112, 2088–2103. [Google Scholar] [CrossRef]
- Richter, R.; Reu, B.; Wirth, C.; Doktor, D.; Vohland, M. The use of airborne hyperspectral data for tree species classification in a species-rich Central European forest area. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 464–474. [Google Scholar] [CrossRef]
- Tao, J.Y.; Liu, L.J.; Pang, Y.; Li, D.Q.; Feng, Y.Y.; Wang, X.; Ding, Y.L.; Peng, Q.; Xiao, W.H. Automatic identification of tree species based on air-borne LiDAR and hyperspectral data. J. Zhejiang Agric. For. Univ. 2018, 35, 314–323. [Google Scholar]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and LiDAR data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree species classification in the Southern Alps based on the fusion of very high geometrical resolution multispectral/hyperspectral images and LiDAR data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Wu, Y.S.; Zhang, X.L. Object-based tree species classification using airborne hyperspectral images and LiDAR data. Forests 2020, 11, 32. [Google Scholar] [CrossRef] [Green Version]
- Kumar, L.; Skidmore, A.K.; Mutanga, O. Leaf level experiments to discriminate between eucalyptus species using high spectral resolution reflectance data: Use of derivatives, ratios and vegetation indices. Geocarto Int. 2010, 25, 327–344. [Google Scholar] [CrossRef]
- Lin, H.J.; Zhang, H.F.; Gao, Y.Q.; Li, X.; Yang, F.; Zhou, Y.F. Mahalanobis distance based hyperspectral characteristic discrimination of leaves of different desert tree species. Spectrosc. Spectr. Anal. 2014, 34, 3358–3362. [Google Scholar]
- Schmidt, K.S.; Skidmore, A.K. Spectral discrimination of vegetation types in a coastal wetland. Remote Sens. Environ. 2003, 85, 92–108. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Castro-Esau, K.L.; Sanchez-Azofeifa, G.A.; Rivard, B.; Wright, S.J.; Quesada, M. Variability in leaf optical properties of Mesoamerican trees and the potential for species classification. Am. J. Bot. 2006, 94, 517–530. [Google Scholar] [CrossRef]
- Dillen, S.Y.; Op de Beeck, M.; Hufkens, K.; Buonanduci, M.; Phillips, N.G. Seasonal patterns of foliar reflectance in relation to photosynthetic capacity and color index in two co-occurring tree species, Quercus rubra and Betula papyrifera. Agric. For. Meteorol. 2012, 160, 60–68. [Google Scholar] [CrossRef]
- Wu, J.; Peng, J.; Wang, M.H.; Xu, J.H.; Gu, L.W. Autumn variation characteristics analysis of leaf spectrum of several common tree species. Spectrosc. Spectr. Anal. 2017, 37, 1225–1231. [Google Scholar]
- Zhao, X.T.; Zhang, S.J.; Liu, J.L.; Sun, H.X. Study on varieties discrimination of nectarine by hyperspectral technology combined with CARS-ELM algorithm. Mod. Food Sci. Technol. 2017, 33, 281–287. [Google Scholar]
- Dietterich, T.G.; Bakiri, G. Solving multiclass learning problems via error-correcting output codes. J. Artif. Intell. Res. 1995, 2, 263–286. [Google Scholar] [CrossRef] [Green Version]
- Dmitriev, E.V.; Kozoderov, V.V.; Dementyev, A.O.; Sokolov, A.A. Recognition of forest species and ages using algorithms based on error-correcting output codes. Eng. Technol. 2017, 10, 794–804. [Google Scholar] [CrossRef] [Green Version]
- Mishra, P.; Nordon, A.; Tschannerl, J.; Lian, G.P.; Redfern, S.; Marshall, S. Near-infrared hyperspectral imaging for non-destructive classification of commercial tea products. J. Food Eng. 2018, 238, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Nazari, S.; Moin, M.S.; Kanan, H.R. Securing templates in a face recognition system using error-correcting output code and chaos theory. Comput. Electr. Eng. 2018, 72, 644–659. [Google Scholar] [CrossRef]
- Escalera, S.; Pujol, O.; Radeva, P. Error-correcting ouput codes library. J. Mach. Learn. Res. 2010, 11, 661–664. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Fowler, J.E.; Zhu, W. On the impact of atmospheric correction on lossy compression of multispectral and hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 130–132. [Google Scholar]
- Yang, R.L.; Su, L.F.; Zhao, X.B.; Wan, H.; Sun, J.G. Representative band selection for hyperspectral image classification. J. Vis. Commun. Image Represent. 2017, 48, 396–403. [Google Scholar] [CrossRef]
- Yang, R.C.; Kan, J.M. An unsupervised hyperspectral band selection method based on shared nearest neighbor and correlation analysis. IEEE Access 2019, 7, 185532–185542. [Google Scholar] [CrossRef]














| Serial Number | Tree Species | Serial Number | Tree Species | Serial Number | Tree Species | Serial Number | Tree Species |
|---|---|---|---|---|---|---|---|
| 1 | Ilex chinensis Sims | 14 | Malus micromalus | 27 | Rosa xanthina Lindl. | 40 | Kolkwitzia amabilis Graebn. |
| 2 | Lonicera maackii | 15 | Syringa pubescens | 28 | Buxus sinica | 41 | Xanthoceras sorbifolium Bunge |
| 3 | Sophora japonica | 16 | Ligustrum quihoui Carr. | 29 | Cytisus scoparius | 42 | Deutzia parviflora Bge. |
| 4 | Amygdalus triloba | 17 | Rosa chinensis Jacq. | 30 | Forsythia koreana‘Sun Gold’ | 43 | Ginkgo biloba L. |
| 5 | Syringa oblata Lindl. | 18 | Swida alba Opiz | 31 | Ligustrum vicaryi Rehder | 44 | Jasminum nudiflorum Lindl. |
| 6 | Kerria japonica | 19 | Forsythia suspensa | 32 | Ulmus pumila L cv‘Jinye’ | 45 | Acer truncatum Bunge |
| 7 | Rhodotypos scandens | 20 | Prunus Cerasifera | 33 | Forsythia viridissima Lindl | 46 | Cercis chinensis Bunge |
| 8 | Weigela florida | 21 | Syringa reticulata var. amurensis | 34 | Paeonia suffruticosa Andr. | 47 | Wisteria sinensis |
| 9 | Acer grosseri Pax | 22 | Amygdalus persica L. var. persica f. duplex Rehd. | 35 | Hibiscus syriacus Linn. | 48 | Lagerstroemia indica L. |
| 10 | Viburnum opulus Linn. | 23 | Pyrus xerophila | 36 | Amygdalus davidiana | 49 | Prunus persica ‘Atropurpurea’ |
| 11 | Cerasus serrulata | 24 | Magnolia soulangeana Soul. Bod. | 37 | Armeniaca sibirica | 50 | Berberis thunbergii var.atropurpurea Chenault |
| 12 | Philadelphus pekinensis Rupr. | 25 | Zanthoxylum | 38 | Crataegus pinnatifida Bunge | ||
| 13 | Chaenomeles speciosa | 26 | Sorbaria kirilowii | 39 | Cotoneaster multiflorus Bge. |
| Spectral Range | Number of Bands | Spectral Resolution | Size of Pixels |
|---|---|---|---|
| 370–1042 nm | 128 | 4.6875 nm | 696 × 520 |
| Training Samples | Spring | Summer | Autumn | |||
|---|---|---|---|---|---|---|
| Test Samples | Summer | Autumn | Spring | Autumn | Spring | Summer |
| OA | 17.98 ± 3.44 | 10.70 ± 2.78 | 17.83 ± 2.58 | 17.73 ± 4.22 | 7.60 ± 2.03 | 10.35 ± 3.83 |
| AA | 17.99 ± 3.55 | 10.64 ± 2.76 | 17.92 ± 2.57 | 17.69 ± 4.17 | 7.64 ± 1.98 | 10.50 ± 3.93 |
| Kappa | 13.61 ± 3.65 | 6.00 ± 2.93 | 13.51 ± 2.72 | 13.44 ± 4.41 | 2.75 ± 2.10 | 5.71 ± 4.07 |
| Training Samples | Campus | Xiling Lake Park |
|---|---|---|
| Test Samples | Xiling Lake Park | Campus |
| OA | 56.01 ± 4.79 | 58.99 ± 4.63 |
| AA | 54.90 ± 4.49 | 58.88 ± 4.61 |
| Kappa | 44.33 ± 5.99 | 48.72 ± 5.78 |
| Methods | OVO | OVA | DR | SR | ELM | Bagging-ELM | SM-ECOC-V1 | SM-ECOC-V2 |
|---|---|---|---|---|---|---|---|---|
| Base classifiers | 1225 | 50 | 56 | 85 | No application | 100 | 85 | 85 |
| Hidden neurons | 120 | 980 | 960 | 690 | 970 | 970 | 550 | 80 |
| Methods | OVO | OVA | DR | SR | ELM | Bagging -ELM | SM-ECOC -V1 | SM-ECOC -V2 |
|---|---|---|---|---|---|---|---|---|
| OA | 95.71 ± 0.38 | 75.68 ± 0.73 | 93.52 ± 0.55 | 89.00 ± 1.18 | 95.60 ± 0.21 | 96.87 ± 0.41 | 94.93 ± 0.52 | 96.98 ± 0.46 |
| AA | 96.94 ± 0.34 | 75.68 ± 0.70 | 94.27 ± 0.76 | 89.09 ± 1.10 | 96.65 ± 0.25 | 97.48 ± 0.41 | 95.85 ± 0.56 | 97.68 ± 0.46 |
| Kappa | 95.58 ± 0.39 | 74.85 ± 0.76 | 93.32 ± 0.56 | 88.67 ± 1.21 | 95.46 ± 0.21 | 96.77 ± 0.43 | 94.77 ± 0.53 | 96.88 ± 0.47 |
| Methods | OVO | OVA | DR | SR | ELM | Bagging -ELM | SM-ECOC -V1 | SM-ECOC -V2 |
|---|---|---|---|---|---|---|---|---|
| OA | 92.00 ± 0.56 | 73.58 ± 0.63 | 90.84 ± 0.44 | 86.45 ± 1.05 | 93.49 ± 0.55 | 93.74 ± 0.38 | 92.64 ± 0.73 | 93.89 ± 0.36 |
| AA | 92.38 ± 0.67 | 75.00 ± 1.14 | 92.49 ± 0.52 | 86.96 ± 1.69 | 95.07 ± 0.64 | 95.14 ± 0.28 | 94.02 ± 0.78 | 95.24 ± 0.34 |
| Kappa | 91.75 ± 0.57 | 72.67 ± 0.66 | 90.56 ± 0.46 | 86.03 ± 1.08 | 93.29 ± 0.57 | 93.54 ± 0.39 | 92.42 ± 0.75 | 93.70 ± 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Kan, J. Classification of Tree Species in Different Seasons and Regions Based on Leaf Hyperspectral Images. Remote Sens. 2022, 14, 1524. https://doi.org/10.3390/rs14061524
Yang R, Kan J. Classification of Tree Species in Different Seasons and Regions Based on Leaf Hyperspectral Images. Remote Sensing. 2022; 14(6):1524. https://doi.org/10.3390/rs14061524
Chicago/Turabian StyleYang, Rongchao, and Jiangming Kan. 2022. "Classification of Tree Species in Different Seasons and Regions Based on Leaf Hyperspectral Images" Remote Sensing 14, no. 6: 1524. https://doi.org/10.3390/rs14061524
APA StyleYang, R., & Kan, J. (2022). Classification of Tree Species in Different Seasons and Regions Based on Leaf Hyperspectral Images. Remote Sensing, 14(6), 1524. https://doi.org/10.3390/rs14061524