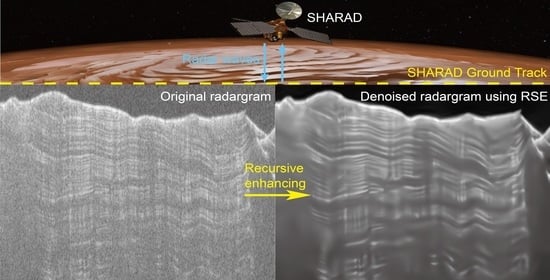
Recursive Enhancement of Weak Subsurface Boundaries and Its Application to SHARAD Data
Abstract
:1. Introduction
2. Data and Method
| Algorithm 1. Recursive subsurface boundary enhancement method *. |
| Input: SHARAD radargram d. |
| Output: Denoised radargram r. |
| Initialization: enhancement coefficient c = 10% |
| and noise variance estimation σi = 10, 50, 80, 100. |
| 1: for k = 1 to 3 do |
| 2: Vertical stacking on d at each adjacent k pixels: dk |
| 3: for j = 1 to 3 do |
| 4: Lateral moving average on dk at adjacent j pixels: s0 |
| 5: Denoise using PID method with σ0:r0 |
| 6: for i = 1 to 3 do |
| 7: Retain local peaks in each trace in ri-1: |
| 8: Superpose to : |
| 9: Denoise using PID method with σi:ri |
| 10: end for |
| 11: return r |
| 12: end for |
| 13: end for |
| * k, j and i are the indices of the iteration. |
3. Numerical Examples
3.1. Synthetic Model
3.2. SHARAD Radargrams
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clifford, S.M.; Crisp, D.; Fisher, D.A.; Herkenhoff, K.E.; Smrekar, S.E.; Thomas, P.C.; Wynn-Williams, D.D.; Zurek, R.W.; Barnes, J.R.; Bills, B.G.; et al. The state and future of Mars polar science and exploration. Icarus 2000, 144, 210–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laskar, J.; Levrard, B.; Mustard, J.F. Orbital forcing of the martian polar layered deposits. Nature 2002, 419, 375–377. [Google Scholar] [CrossRef] [PubMed]
- Malin, M.C.; Danielson, G.E.; Ingersoll, A.P.; Masursky, H.; Veverka, J.; Ravine, M.A.; Soulanille, T.A. Mars Observer camera. J. Geophys. Res. 1992, 97, 7699–7718. [Google Scholar] [CrossRef]
- McEwen, A.S.; Eliason, E.M.; Bergstrom, J.W.; Bridges, N.T.; Hansen, C.J.; Delamere, W.A.; Grant, J.A.; Gulick, V.C.; Herkenhoff, K.E.; Keszthelyi, L.; et al. Mars Reconnaissance Orbiter’s High Resolution Imaging Science Experiment (HiRISE). J. Geophys. Res. 2007, 112, E05S02. [Google Scholar] [CrossRef] [Green Version]
- Byrne, S. Internal structure of the Martian south polar layered deposits. J. Geophys. Res. 2004, 109, E11001. [Google Scholar] [CrossRef]
- Kolb, E.J.; Tanaka, K.L. Accumulation and erosion of south polar layered deposits in the Promethei Lingula region, Planum Australe, Mars. Int. J. Mars Sci. Explor. 2006, 2, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Milkovich, S.M.; Plaut, J.J. Martian South Polar Layered Deposit stratigraphy and implications for accumulation history. J. Geophys. Res. 2008, 113, E06007. [Google Scholar] [CrossRef] [Green Version]
- Seu, R.; Phillips, R.J.; Biccari, D.; Orosei, R.; Masdea, A.; Picardi, G.; Safaeinili, A.; Campbell, B.A.; Plaut, J.J.; Marinangeli, L.; et al. SHARAD sounding radar on the Mars Reconnaissance Orbiter. J. Geophys. Res. 2007, 112, E05S05. [Google Scholar] [CrossRef]
- Jordan, R.; Picardi, G.; Plaut, J.; Wheeler, K.; Kirchner, D.; Safaeinili, A.; Johnson, W.; Seu, R.; Calabrese, D.; Zampolini, E.; et al. The Mars express MARSIS sounder instrument. Planet. Space Sci. 2009, 57, 1975–1986. [Google Scholar] [CrossRef]
- Nunes, D.C.; Phillips, R.J. Radar subsurface mapping of the polar layered deposits on Mars. J. Geophys. Res. 2006, 111, E06S21. [Google Scholar] [CrossRef] [Green Version]
- Campbell, B.A.; Morgan, G.A.; Bernardini, F.; Putzig, N.E.; Nunes, D.C.; Plaut, J.J. Calibration of Mars Reconnaissance Orbiter Shallow Radar (SHARAD) data for subsurface probing and surface reflectivity studies. Icarus 2021, 360, 114358. [Google Scholar] [CrossRef]
- Yuan, Y.; Wu, Y.; Fu, Y.; Wu, Y.; Zhang, L.; Jiang, Y. An advanced SAR image despeckling method by bernoulli-sampling-based self-supervised deep learning. Remote Sens. 2021, 13, 3636. [Google Scholar] [CrossRef]
- Mohan, E.; Rajesh, A.; Sunitha, G.; Konduru, R.M.; Avanija, J.; Ganesh Babu, L. A deep neural network learning-based speckle noise removal technique for enhancing the quality of synthetic-aperture radar images. Concurr. Comput. Pract. Exp. 2021, 33, e6239. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W. Application of denoising CNN for noise suppression and weak signal extraction of lunar penetrating radar data. Remote Sens. 2021, 13, 779. [Google Scholar] [CrossRef]
- Lee, J.S. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 165–168. [Google Scholar] [CrossRef] [Green Version]
- Rubel, O.; Lukin, V.; Rubel, A.; Egiazarian, K. Selection of lee filter window size based on despeckling efficiency prediction for sentinel SAR images. Remote Sens. 2021, 13, 1887. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–166. [Google Scholar] [CrossRef]
- Lopes, A.; Nezry, E.; Touzi, R.; Laur, H. Structure detection and statistical adaptive speckle filtering in SAR images. Int. J. Remote Sens. 2010, 14, 1735–1758. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A tutorial on speckle reduction in synthetic aperture radar images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef] [Green Version]
- Knaus, C.; Zwicker, M. Progressive image denoising. IEEE Trans. Image Process. 2014, 23, 3114–3125. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, J. Progressive denoising of seismic data via robust noise estimation in dual domains. Geophysics 2020, 85, V99–V118. [Google Scholar] [CrossRef]
- Courville, S.W.; Perry, M.R.; Putzig, N.E. Lower bounds on the thickness and dust content of layers within the north polar layered deposits of Mars from radar forward modeling. Planet. Sci. J. 2021, 2, 28. [Google Scholar] [CrossRef]
- Whitten, J.L.; Campbell, B.A. Lateral continuity of layering in the Mars south polar layered deposits from SHARAD sounding data. J. Geophys. Res. Planets 2018, 123, 1541–1554. [Google Scholar] [CrossRef]
- Putzig, N.E.; Smith, I.B.; Perry, M.R.; Foss, F.J., 2nd; Campbell, B.A.; Phillips, R.J.; Seu, R. Three-dimensional radar imaging of structures and craters in the Martian polar caps. Icarus 2018, 308, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Milkovich, S.M.; Plaut, J.J.; Safaeinili, A.; Picardi, G.; Seu, R.; Phillips, R.J. Stratigraphy of Promethei Lingula, south polar layered deposits, Mars, in radar and imaging data sets. J. Geophys. Res. 2009, 114, E03002. [Google Scholar] [CrossRef] [Green Version]
- Guallini, L.; Rossi, A.P.; Forget, F.; Marinangeli, L.; Lauro, S.E.; Pettinelli, E.; Seu, R.; Thomas, N. Regional stratigraphy of the south polar layered deposits (Promethei Lingula, Mars): “Discontinuity-bounded” units in images and radargrams. Icarus 2018, 308, 76–107. [Google Scholar] [CrossRef] [Green Version]
- Seu, R.; Phillips, R.J.; Alberti, G.; Biccari, D.; Bonaventura, F.; Bortone, M.; Calabrese, D.; Campbell, B.A.; Cartacci, M.; Carter, L.M.; et al. Accumulation and erosion of Mars’ south polar layered deposits. Science 2007, 317, 1715–1718. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.E.; Zuber, M.T.; Frey, H.V.; Garvin, J.; Head, J.W.; Muhleman, D.O.; Pettengill, G.H.; Phillips, R.J.; Solomon, S.C.; Zwally, H.J.; et al. Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars. J. Geophys. Res. 2001, 106, 23689–23722. [Google Scholar] [CrossRef]
- Choudhary, P.; Holt, J.W.; Kempf, S.D. Surface clutter and echo location analysis for the interpretation of SHARAD data from Mars. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1285–1289. [Google Scholar] [CrossRef]
- Hamran, S.E.; Paige, D.A.; Amundsen, H.E.; Berger, T.; Brovoll, S.; Carter, L.; Damsgård, L.; Dypvik, H.; Eide, J.; Eide, S.; et al. Radar imager for Mars’ subsurface experiment—RIMFAX. Space Sci. Rev. 2020, 216, 1–39. [Google Scholar] [CrossRef]
- Zhou, B.; Shen, S.; Lu, W.; Liu, Q.; Tang, C.; Li, S.; Fang, G. The Mars rover subsurface penetrating radar onboard China’s Mars 2020 mission. Earth Planet. Phys. 2020, 4, 1–10. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, T.; Jia, Y.; Peng, S.; Yan, C. Zhurong: Features and mission of China’s first Mars rover. Innov. 2021, 2, 100121. [Google Scholar] [CrossRef]
- Fang, G.Y.; Zhou, B.; Ji, Y.C.; Zhang, Q.Y.; Shen, S.X.; Li, Y.X.; Guan, H.F.; Tang, C.J.; Gao, Y.Z.; Lu, W.; et al. Lunar penetrating radar onboard the Chang’e-3 mission. Res. Astron. Astrophys. 2014, 14, 1607–1622. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, B.; Lin, Y.; Zhu, M.-H.; Song, H.; Dong, Z.; Gao, Y.; Di, K.; Yang, W.; Lin, H.; et al. Lunar regolith and substructure at Chang’E-4 landing site in South Pole–Aitken basin. Nat. Astron. 2021, 5, 25–30. [Google Scholar] [CrossRef]
- Fa, W. Simulation for ground penetrating radar (GPR) study of the subsurface structure of the Moon. J. Appl. Geophys. 2013, 99, 98–108. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, W.; Hu, S.; Lin, Y.; Fang, G.; Li, C.; Peng, W.; Zhu, S.; He, Z.; Zhou, B.; et al. Volcanic history of the Imbrium basin: A close-up view from the lunar rover Yutu. Proc. Natl. Acad. Sci. USA 2015, 112, 5342–5347. [Google Scholar] [CrossRef] [Green Version]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, P.; Zhang, J. Recursive Enhancement of Weak Subsurface Boundaries and Its Application to SHARAD Data. Remote Sens. 2022, 14, 1525. https://doi.org/10.3390/rs14061525
Fang P, Zhang J. Recursive Enhancement of Weak Subsurface Boundaries and Its Application to SHARAD Data. Remote Sensing. 2022; 14(6):1525. https://doi.org/10.3390/rs14061525
Chicago/Turabian StyleFang, Peng, and Jinhai Zhang. 2022. "Recursive Enhancement of Weak Subsurface Boundaries and Its Application to SHARAD Data" Remote Sensing 14, no. 6: 1525. https://doi.org/10.3390/rs14061525
APA StyleFang, P., & Zhang, J. (2022). Recursive Enhancement of Weak Subsurface Boundaries and Its Application to SHARAD Data. Remote Sensing, 14(6), 1525. https://doi.org/10.3390/rs14061525