Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake
Abstract
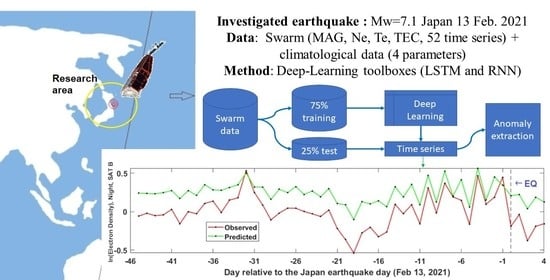
:1. Introduction
1.1. Case Study
1.2. Data
2. Methodology
3. Observations
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geller, R.J. Earthquake prediction: A critical review. Geophys. J. Int. 1997, 131, 425–450. [Google Scholar] [CrossRef] [Green Version]
- Parrot, M. Use of satellites to detect seismo-electromagnetic effects, Main phenomenological features of ionospheric precursors of strong earthquakes. Adv. Space Res. 1995, 15, 1337–1347. [Google Scholar] [CrossRef]
- Hayakawa, M.; Molchanov, O.A. Seismo- Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling. In Seismo Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling; Terra Scientific Publishing Co.: Tokyo, Japan, 2002; p. 477. [Google Scholar]
- Pulinets, S.; Boyarchuk, K.A. Ionospheric Precursors of Earthquakes; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Freund, F. Stress-activated positive hole charge carriers in rocks and the generation of pre-earthquake signals. In Electromagnetic Phenomena Associated with Earthquakes; Hayakawa, M., Ed.; Transworld Research Network: Trivandrum, India, 2009; pp. 41–96. [Google Scholar]
- Pulinets, S.; Ouzounov, D. Lithosphere-Atmosphere-Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Pokhotelov, O.A. Model for the VLF/LF radio signal anomalies formation associated with earthquakes. Adv. Space Res. 2014, 54, 2532–2539. [Google Scholar] [CrossRef]
- Liu, J.Y. Seismo-ionospheric precursors of the 2017 M7.3 Iran-Iraq Border Earthquake and the 2018 M5.9 Osaka Earthquake observed by FORMOSAT-5/AIP. In Proceedings of the EMSEV 2018, International Workshop Integrating Geophysical Observations from Ground to Space for Earthquake and Volcano Investigations Potenza, Basilicata, Italy, 17–21 September 2018. [Google Scholar]
- Akhoondzadeh, M.; Parrot, M.; Saradjian, M.R. Electron and ion density variations before strong earthquakes (M > 6.0) using DEMETER and GPS data. Nat. Hazards Earth Syst. Sci. 2010, 10, 7–18. [Google Scholar] [CrossRef] [Green Version]
- De Santis, A.; De Franceschi, G.; Spogli, L.; Perrone, L.; Alfonsi, L.; Qamili, E.; Cianchini, G.; Di Giovambattista, R.; Salvi, S.; Filippi, E.; et al. Geospace perturbations induced by the Earth: The state of the art and future trends. Phys. Chem. Earth 2015, 85-86, 17–33. [Google Scholar] [CrossRef] [Green Version]
- Deb, A.; Gazi, M.; Barman, C. Anomalous soil radon fluctuations—signal of earthquakes in Nepal and eastern India regions. J. Earth Syst. Sci. 2016, 125, 1657–1665. [Google Scholar] [CrossRef]
- Kojima, H.; Yoshino, C.; Nemoto, K.; Hattori, K.; Konishi, T.; Furuya, R. Multi-channel singular spectrum analysis of underground Rn concentration at Asahi station, Boso Peninsula, Japan: Preliminary report on relation between the variation of underground Rn flux and the local seismic activity. JAE Lett. 2020, 39, 46–51. [Google Scholar] [CrossRef]
- Freund, F.; Ouillon, G.; Scoville, J.; Sornette, D. Earthquake precursors in the light of peroxy defects theory: Critical review of systematic observations. Eur. Phys. J. Spec. Top. 2021, 230, 7–46. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An improved coupling model for the lithosphere-atmosphere-ionosphere system. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- Akhoondzadeh, M. A MLP neural network as an investigator of TEC time series to detect seismo-ionospheric anomalies. Adv. Space Res. 2013, 51, 2048–2057. [Google Scholar] [CrossRef]
- Akhoondzadeh, M. Anomalous TEC variations associated with the powerful Tohoku earthquake of 11 March 2011. Nat. Hazards Earth Syst. Sci. 2012, 12, 1453–1462. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Zhao, D. Upper and lower plate controls on the great 2011 Tohoku-oki earthquake. Sci. Adv. 2018, 4, eaat4396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bagiya, M.S.; Thomas, D.; Astafyeva, E.; Bletery, Q.; Lognonné, P.; Ramesh, D.S. The Ionospheric view of the 2011 Tohoku-Oki earthquake seismic source: The first 60 seconds of the rupture. Sci. Rep. 2020, 10, 5232. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Seismicity of the Earth and Associated Phenomena, 2nd ed.; Princeton, N.J., Ed.; Princeton University Press: Princeton, NJ, USA, 1954. [Google Scholar]
- De Santis, A.; Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory worldwide signatures of earthquake occurrences on Swarm satellite data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef] [Green Version]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field, Earth. Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Léger, J.M.; Jager, T.; Bertrand, F.; Hulot, G.; Brocco, L.; Vigneron, P.; Lalanne, X.; Chulliat, A.; Fratter, I. In-flight performance of the Absolute Scalar Magnetometer vector mode on board the Swarm satellites. Earth Planets Space 2015, 67, 57. [Google Scholar] [CrossRef] [Green Version]
- Merayo, J.M.; Jørgensen, J.L.; Friis-Christensen, E.; Brauer, P.; Primdahl, F.; Jørgensen, P.S.; Allin, T.H.; Denver, T. The Swarm Magnetometry Package. In Small Satellites for Earth Observation; Sandau, R., Röser, H.P., Valenzuela, A., Eds.; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.-E.; Åhlen, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys Res. Space Phys. 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- Haagmans, R.; Bock, R.; Rider, H. Swarm; ESA’s Magnetic Field Mission. 2013. Available online: https://earth.esa.int/documents/700255/1805948/ESA+magnetic+field+mission/36942f02-b2d4-4787-af81-eb19efb74265 (accessed on 15 January 2022).
- van den IJssel, J.; Forte, B.; Montenbruck, O. Impact of Swarm GPS receiver updates on POD performance. Earth Planets Space 2016, 68, 85. [Google Scholar] [CrossRef] [Green Version]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Shen, X. Swarm-TEC Satellite Measurements as a Potential Earthquake Precursor Together with Other Swarm and CSES Data: The Case of Mw7.6 2019 Papua New Guinea Seismic Event. Front. Earth Sci. 2022, 10, 820189. Available online: https://www.frontiersin.org/articles/10.3389/feart.2022.820189 (accessed on 15 January 2022). [CrossRef]
- De Santis, A.; Balasis, G.; Pavón-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential earthquake precursory pattern from space: The 2015 Nepal event as seen by magnetic Swarm satellites. Earth Planet Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Piscini, A.; Cianchini, G. Multi precursors analysis associated with the powerful Ecuador (Mw = 7.8) earthquake of 16 April 2016 using Swarm satellites data in conjunction with other multi-platform satellite and ground data. Adv. Space Res. 2018, 61, 248–263. [Google Scholar] [CrossRef] [Green Version]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Piscini, A.; Jin, S. Anomalous seismo-LAI variations potentially associated with the 2017 Mw = 7.3 Sarpol-e Zahab (Iran) earthquake from Swarm satellites, GPS-TEC and climatological data. Adv. Space Res. 2019, 64, 143–158. [Google Scholar] [CrossRef]
- Marchetti, D.; Akhoondzadeh, M. Analysis of Swarm satellites data showing seismo-ionospheric anomalies around the time of the strong Mexico (Mw=8.2) earthquake of 08 September 2017. Adv. Space Res. 2018, 62, 614–623. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Piscini, A.; Campuzano, S.; De Carvalho, W.V.J.O. Pre-earthquake chain processes detected from ground to satellite altitude in preparation of the 2016–2017 seismic sequence in Central Italy. Remote Sens. Environ. 2019, 229, 93–99. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Shen, X.; Campuzano, S.A.; Perrone, L.; Piscini, A.; Giovambattista, R.D.; Jin, S.; Ippolito, A.; Cianchini, G.; et al. Possible Lithosphere-Atmosphere-Ionosphere Coupling effects prior to the 2018 Mw = 7.5 Indonesia earthquake from seismic, atmospheric and ionospheric data. J. Asian Earth Sci. 2020, 188, 104097. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Marchetti, D.; Piscini, A.; Sabbagh, D.; Perrone, L.; Campuzano, S.A.; Inan, S. A multiparametric approach to study the preparation phase of the 2019 M7.1 Ridgecrest (California, USA) Earthquake. Front. Earth Sci. 2020, 8, 540398. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Matzka, J.; Bronkalla, O.; Tornow, K.; Elger, K.; Stolle, C. Geomagnetic Kp index. V. 1.0. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Nose, M.; Iyemori, T.; Sugiura, M.; Kamei, T. World Data Center for Geomagnetism. Geomagn. Dst Index 2015. [Google Scholar] [CrossRef]
- Dobrovolsky, I.R.; Zubkov, S.I.; Myachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Thébault, E.; Finlay, C.C.; Beggan, C.D.; Alken, P.; Aubert, J.; Barrois, O.; Bertrand, F.; Bondar, T.; Boness, A.; Brocco, L.; et al. International Geomagnetic Reference Field: The 12th generation. Earth Planets Space 2015, 67, 79. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), American Meteorological Society—Modern-Era Retrospective analysis for Research and Applications version 2 (MERRA-2) special collection. J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Parkinson, C.L. Aqua: An Earth-Observing Satellite mission to examine water and other climate variables. IEEE Trans. Geosci. Remote Sens. 2003, 41, 173–183. [Google Scholar] [CrossRef]
- Piscini, A.; Marchetti, D.; De Santis, A. Multi-parametric climatological analysis associated with global significant volcanic eruptions during 2002–2017. Pure Appl. Geophys. 2019, 176, 3629–3647. [Google Scholar] [CrossRef]
- Scholz, C. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Rikitake, T. Earthquake precursors in Japan: Precursor time and detectability. Tectonophysics 1987, 136, 265–282. [Google Scholar] [CrossRef]
- Piscini, A.; De Santis, A.; Marchetti, D.; Cianchini, G. A Multiparametric Climatological Approach to Study the 2016 Amatrice–Norcia (Central Italy) Earthquake Preparatory Phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. The Possibility of Earthquake Forecasting; Learning from Nature; IOP Publ.: Bristol, UK, 2018. [Google Scholar]

















| Parameter | Value |
|---|---|
| Layers | 3 |
| No. of features in sequence input layer | 1 |
| No. of hidden units in LSTM layer | 200 |
| No. of responses in fully connected layer | 1 |
| Max epochs | 300 |
| Initial learning rate | 0.005 |
| Solver | Adam |
| Gradient threshold | 1 |
| Detected Anomalies Using Median/Interquartile Method | |||||
|---|---|---|---|---|---|
| Satellite | Measured Parameter (D: Day, N: Night) | Anomalous Day | Sorted by Voting | ||
| Day | Rank | ||||
| Swarm Alpha | Electron Density | D | −13 | −32 −31 −6 −8 −1 −13 −18 −9 −15 −5 −20 −21 −23 −27 −30 −4 −11 −16 −24 −2 −12 −25 −26 −28 −33 −36 −3 −10 −14 −22 −29 −17 −34 −35 | (13) (12) (11) (9) (8) (8) (7) (6) (6) (5) (5) (5) (5) (5) (5) (4) (4) (4) (4) (3) (3) (3) (3) (3) (3) (3) (2) (2) (2) (2) (2) (1) (1) (1) |
| N | −31, −32 | ||||
| Electron Temperature | D | −12 to −16 | |||
| N | −−− | ||||
| Magnetic Scalar | D | −2, −4, −5, −6, −8, −9, −18 | |||
| N | −11, −22, −31 to −33 | ||||
| Magnetic Vector x | D | −4, −5, −6, −8, −9, −18 | |||
| N | −11, −22, −31 to −33 | ||||
| Magnetic Vector y | D | −6, −8, −9, −20, −27 | |||
| N | −1, −8, −13, −32 | ||||
| Magnetic Vector z | D | −1, −34 | |||
| N | −3, −21, −31 | ||||
| Slant TEC | D | −11, −13, −21 | |||
| N | −12, −16, −20, −31 | ||||
| Vertical TEC | D | −21, −36 | |||
| N | −5, −20 | ||||
| Swarm Bravo | Electron Density | D | −24, −32 | ||
| N | −1, −4, −32 | ||||
| Electron Temperature | D | −6, −18, −23, −27 | |||
| N | −15, −23 | ||||
| Magnetic Scalar | D | −6, −18 | |||
| N | −1, −10, −31, −32 | ||||
| Magnetic Vector x | D | −6, −18 | |||
| N | −10, −23, −31 to −33 | ||||
| Magnetic Vector y | D | −−−−− | |||
| N | −1, −8, −22, −23, −35 | ||||
| Magnetic Vector z | D | −−−−− | |||
| N | −−−−− | ||||
| Slant TEC | D | −30, −32 | |||
| N | −−−−− | ||||
| Vertical TEC | D | −20, −24, −30, −32 | |||
| N | −5, −8 | ||||
| Swarm Charlie | Electron Density | D | −6, −13 | ||
| N | −31, −32, −36 | ||||
| Electron Temperature | D | −1, −3, −8, −9, −13 to −18, −27 to −30 | |||
| N | −16, −23 to −30 | ||||
| Magnetic Scalar | D | −2, −4, −5, −6, −8, −9, −18, −26 | |||
| N | −11, −24, −31, −32 | ||||
| Magnetic Vector x | D | −5, −6, −8, −9, −18 | |||
| N | −31, −32 | ||||
| Magnetic Vector y | D | −6, −20, −27 | |||
| N | −1, −10, −32 | ||||
| Magnetic Vector z | D | −1, −6, −25, −31 | |||
| N | −21, −31 | ||||
| Slant TEC | D | −33 | |||
| N | −15 | ||||
| Vertical TEC | D | −21, −36 | |||
| N | −11 | ||||
| Swarm Alpha-Charlie | Electron Density | D | −6, −8, −9, −13, −15 | ||
| N | −2, −4, −31 | ||||
| Electron Temperature | D | −12, −13, −15, −26, −30 | |||
| N | −25, −28 | ||||
| Detected Anomalies Using LSTM Method | |||||
|---|---|---|---|---|---|
| Satellite | Measured Parameter (D: Day, N: Night) | Anomalous Day | Sorted by Voting | ||
| Day | Rank | ||||
| Swarm Alpha | Electron Density | D | −6, −13 | −31 −32 −8 −5 −13 −1 −23 −6 −21 −9 −22 −3 −12 −15 −18 −4 −24 −2 −14 −16 −17 −25 −20 −26 −30 −35 −10 −28 −29 −33 | (18) (14) (13) (12) (11) (10) (10) (9) (8) (7) (7) (6) (5) (5) (5) (4) (4) (4) (4) (3) (3) (3) (3) (2) (2) (2) (1) (1) (1) (1) |
| N | −1, −4, −31, −32 | ||||
| Electron Temperature | D | −12, −13, −15 | |||
| N | −1, −8, −24 | ||||
| Magnetic Scalar | D | −2, 4, −5, −6, −8, −9, −26 | |||
| N | −11, −22, −31, −32 | ||||
| Magnetic Vector x | D | −1, −3, −6 | |||
| N | −11, −18, −22, −31, −32 | ||||
| Magnetic Vector y | D | −6, −8 | |||
| N | −1, −18, −32 | ||||
| Magnetic Vector z | D | −5, −11, −35 | |||
| N | −3, −6, −18, −21, −29, −31 | ||||
| Slant TEC | D | −3, −5, −11, −13, −21 | |||
| N | −5, −16, −20, −31 | ||||
| Vertical TEC | D | −11, −21, −26 | |||
| N | −5, −13, | ||||
| Swarm Bravo | Electron Density | D | −6, −11, −21, −22, −24, −32 | ||
| N | −1, −3, −4, −16,−20, −31, −32 | ||||
| Electron Temperature | D | −6, −18, −23,−31, −32, −35 | |||
| N | −15, −16, −23 | ||||
| Magnetic Scalar | D | −6, −17 | |||
| N | −1, −31, −32 | ||||
| Magnetic Vector x | D | −6 | |||
| N | −1, −22, −23, −31, −32 | ||||
| Magnetic Vector y | D | −12, −13, −25 | |||
| N | −1, −15, −20, −22, −23, −30, −31, −42 | ||||
| Magnetic Vector z | D | −8, −13, −18 | |||
| N | −23 | ||||
| Slant TEC | D | −21, −31, −32 | |||
| N | −5, −8, −11, −31 | ||||
| Vertical TEC | D | −30, −32 | |||
| N | −5, −32 | ||||
| Swarm Charlie | Electron Density | D | −8, −9,−13, −14, −22, −23 | ||
| N | −5, −8, −9, −31, −32 | ||||
| Electron Temperature | D | −1, −3 | |||
| N | −16 | ||||
| Magnetic Scalar | D | −4, −6, −8, −9 | |||
| N | −11, −24, −31, −32 | ||||
| Magnetic Vector x | D | −1, −3, −22, −23, −24, −25 | |||
| N | −11, −22, −31, −32 | ||||
| Magnetic Vector y | D | −8, −9 | |||
| N | −1, −10, −32 | ||||
| Magnetic Vector z | D | −5, −8, −9, −13, −14 | |||
| N | −18, −31 | ||||
| Slant TEC | D | −3, −5, −14, −21 | |||
| N | −15, −33 | ||||
| Vertical TEC | D | −21, −31 | |||
| N | −2, −5, −8 | ||||
| Swarm Alpha-Charlie | Electron Density | D | 5, −9, −13, −15 | ||
| N | −23, −31 | ||||
| Electron Temperature | D | −6, −8, −12, −13, −15, −34 | |||
| N | −25, −28 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Wang, T. Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake. Remote Sens. 2022, 14, 1582. https://doi.org/10.3390/rs14071582
Akhoondzadeh M, De Santis A, Marchetti D, Wang T. Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake. Remote Sensing. 2022; 14(7):1582. https://doi.org/10.3390/rs14071582
Chicago/Turabian StyleAkhoondzadeh, Mehdi, Angelo De Santis, Dedalo Marchetti, and Ting Wang. 2022. "Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake" Remote Sensing 14, no. 7: 1582. https://doi.org/10.3390/rs14071582
APA StyleAkhoondzadeh, M., De Santis, A., Marchetti, D., & Wang, T. (2022). Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake. Remote Sensing, 14(7), 1582. https://doi.org/10.3390/rs14071582