Mothership-Cubesat Radioscience for Phobos Geodesy and Autonomous Navigation

Abstract

The knowledge of the interior structure (e.g., homogeneous, porous, or fractured) of Martian moons will lead to a better understanding of their formation as well as the early solar system. One approach to inferring the interior structure is via geodetic characteristics, such as gravity field and libration. Geodetic parameters can be derived from radiometric tracking measurements. A feasible mothership-CubeSat mission is proposed in this study with following purposes, (1) performing inter-sat Doppler measurements, (2) improving the understanding of Phobos as well as the dynamic model, (3) securing the mothership as well as the primary mission, and (4) supporting autonomous navigation, given the long distance between the Earth and Mars. This study analyzes budgets of volume, mass, power, deployment $\Delta v$, and link, and the Doppler measurement noise of the system, and gives a feasible design for the CubeSat. The accuracy of orbit determination and geodesy is revealed via the Monte-Carlo simulation of estimation considering all uncertainties. Under an ephemeris error of the Mars-Phobos system ranging from 0 to 2 km, the autonomous orbit determination delivers an accuracy ranging from 0.2 m to 21 m and 0.05 mm/s to 0.4 cm/s. The geodesy can return 2nd-degree gravity coefficients at an accuracy of 1‰, even in the presence of an ephemeris error of 2 km. The achieved covariance of gravity coefficients and libration amplitude indicates an excellent possibility to distinguish families of interior structures.

1. Introduction

The Martian moons, Phobos and Deimos, are of great scientific interest. The origins of these moons remain unclear. They could possibly be captured C-type asteroids or formed from post-impact debris discs of Mars [1,2]. If they were asteroids, they might play a role in transporting water to terrestrial planets, such as Mars and the Earth [3,4]. Understanding the interior structure of Phobos can put constraints on the formation of Martain moons, as well as that of the early solar system. In addition to the endeavors of Phobos-1 and -2 in the late 1980s, many mission concepts, such as the Phobos-Grunt, PHOOTPRINT, MERLIN, and MMX, for exploring the Martian moons have been proposed and intensively studied by space agencies [4,5,6,7,8]. A mothership-CubeSat radioscience mission is proposed in this paper for probing Phobos and supporting autonomous navigation at the Martian distance from the Earth.

Le Maistre et al. [9] have classified the interior structure of Phobos into four families: rubble pile, heavily fractured, porous, and icy body. The interior structure can be inferred from the moments of inertia (MoI) of Phobos. The MoI is related to the central gravitational parameter, $GM$, 2nd-degree gravity coefficients, $C_{20}$ and $C_{22}$, and libration amplitude. A number of flybys performed in past missions (e.g., the Viking, Phobos-2, and Mars Express) provided valuable radio tracking data that elucidated the $GM$ of Phobos. One latest $GM$ derived radio tracking data during flybys has an uncertainty of 0.3% [10]. The estimation of Phobos’ ephemeris and 2nd-degree gravity coefficients done by Jacobson and Lainey [11] shows an 8.7% disagreement on $C_{22}$ from that of the homogeneous model, which corresponds to the shape model derived from observed images [12,13]. While the accuracies of the estimated $C_{20}$ and $C_{22}$ were stated to be 6% and 3% [11], respectively, these results are dependent upon the used quadrupole model of Phobos and the measured libration amplitude (i.e., $1.{14}^{\circ }$ [14]). The libration amplitude estimated based on images has an uncertainty ranging from 2% to 10%, which is in turn dependent on the used ephemeris data [14]. A confident accuracy should be evaluated by considering all uncertainties in the model and measurements.

One latest estimation attempt based on radio tracking data has 1-$\sigma$ uncertainties of 8% and 30% on $C_{20}$ and $C_{22}$, respectively [15]. However, accuracies of 3–5% on $C_{20}$, $C_{22}$, and the libration amplitude are desirable for the identification of the interior structure [9,16]. Nevertheless, the past radio tracking is subject to the flyby geometry relative to the ground station, and the gravity signature is limited by the short duration (i.e., generally <1 h) and far distance (i.e., generally >80 km) of flybys. Consequently, the gravity coefficients $C_{20}$ and $C_{22}$ cannot be resolved at an accuracy sufficient for drawing conclusions on the mass distribution [17]. In addition, Phobos is a secondary body orbiting a primary body, Mars. The gravity and position of the primary can significantly influence the dynamical environment of the secondary as well as the effect of geodesy. Rosenblatt et al. [18] and Yan et al. [19] stated that the error of estimated $C_{20}$ will increase by a few 10% as the ephemeris error tends to a few 100 m. Furthermore, the ephemeris error can go up to a few kilometers by the time of the MMX mission (i.e., 2025–2027) if the ephemeris is not updated. Chen et al. [20] also showed the impact of Phobos’ ephemeris errors on spacecraft orbit determination and parameter identification. In summary, ephemeris errors, gravity coefficients, and libration amplitude of Phobos, and orbits of spacecraft are closely correlated in the estimation. It is not only important to enable an observation manner more effective than distant flybys, but also necessary to evaluate the estimation accuracy considering all uncertainties.

Concerning a more effective approach to probing Phobos, there have been several mission concepts and flight plans proposed, the corresponding geodesy performance of which was also evaluated (e.g., [19,21,22,23]). However, most of the error analyses for the proposed concepts were conducted through analytical covariance analyses. With the high non-linearity related to the flight dynamics and many local optima related to the many variables (e.g., spacecraft orbit states and geodetic parameters) to estimate in the problem, in practice, the theoretical covariance obtained at the global optimum might not be achieved. For the mission proposed in this study, the estimation model is described in Section 4, based on which the theoretical covariance is computed. Massive estimation simulations, which consider all kinds of uncertainties in the model and measurements, are performed to reveal practical covariance (see Section 5). The difference between the theoretical and practical covariances can indicate the functionality of the estimation algorithm and the need for statistical examinations. Despite the difference from the theoretical covariance, the low practical covariance indicates an excellent possibility to distinguish families of interior structures (see Section 6).

The proposed mission concept is designed to feasibly support the desired geodesy and the entire mission. NanoSats have started to play a role in planetary missions. As they are small and low-cost, they can be carried by a mother spacecraft and then deployed to perform audacious flight or landing, or cooperative operations along with the mother spacecraft. There have been several planetary NanoSat missions, such as Philae, MASCOT, MarCo, HERA-Juventas, HERA-Milani [24,25,26], and ideas (e.g., [23,27,28,29,30]). It is proposed in this paper that a CubeSat is carried and deployed by the mother spacecraft aimed for Phobos. The two probes will fly in different quasi-satellite orbits about Phobos, and perform inter-satellite Doppler measurements (see Section 2). The advantage is multiple-fold. First, the measurement is independent of the ground station and thus can support autonomous navigation, and consequently, enhance the safety of the main mission. Second, the longduration proximity orbiting will bear an evident signature of the geodetic characteristics of Phobos. As for feasibility, this paper analyzes budgets of volume, mass, power, deployment $\Delta v$, and link, and the measurement noise of the system, and gives a detailed design of the CubeSat (see Section 3).

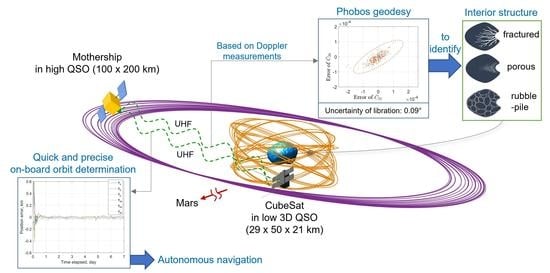
2. Mission Profile and Orbits

It is proposed that the CubeSat boards the mother spacecraft aimed for Phobos. As precise knowledge on the target is lacking in the beginning, it is preferred that the less indispensable CubeSat is deployed from the mothership to a low-altitude orbit about Phobos, which is sensitive to geodetic parameters of the target, while the mothership stays in a high orbit, which is safe from escape and impact on the target. The two-way Doppler measurement is performed between the two orbiting probes, where the radio signal is triggered by the mothership and reflected by the CubeSat. Section 3.2 will give details on this setup. Based on the inter-satellite measurements, spacecraft orbits can be determined, and the geodetic characteristics of Phobos can be identified. Figure 1 schematically depicts the proposed radioscience mission.

The irregularily shaped Phobos has dimensions of $26\times 22\times 18$ km. As it is much more smaller than Mars, whose dimension is 6780 km, and orbits closely (i.e., with a semi-major axis of 9377.2 km) around Mars, dynamics in its vicinity is dominated by the gravity of Mars. The sphere of influence of Phobos is small and even below its surface. Therefore, classical Keplerian orbits do not exist around Phobos. The retrograde quasi-satellite orbit (QSO) found in the Mars-Phobos three-body problem is a means for spacecraft to orbit around Phobos in the sense of relative motion [31,32]. Previous work has computed a database of periodic three-dimensional QSO (3D QSO) around Phobos in the circular-restricted three-body problem (CR3BP) [33,34]. Figure 2 presents families of periodic QSO described by the x-amplitude, $A_x$, and z-amplitude, $A_z$. The sensitivity of the orbits to the injection epoch, presumed ground-based orbit determination error (i.e., 1-$\sigma$ 50 m and 3 cm/s on each component), and $\Delta v$ execution error (i.e., 1-$\sigma$ 1.4 cm/s on each component) has been investigated by propagating the orbits for one week in the presence of the perturbations [34,35]. The color scale in the Figure 2 represents the effective stability of the QSO according to results of sensitivity analyses, which reveals the stability region of bounded orbits around Phobos. The super- and hyper-stable orbits can stay bounded for an acceptable duration (i.e., >7 days) in the high-fidelity model. Low-altitude orbits are generally sensitive to the gravity field of the target, and high-inclination orbits are particularly sensitive to the zonal gravity harmonics [16,22]. Therefore, a low-altitude and high-inclination 29 × 50 × 21 km (in $A_x\times A_y\times A_z$ format, where $A_y$ is the y-amplitude) 3D QSO, which is marked with a black circle and indicated hyper-stable in Figure 2 and shown to be easily maintainable in Refs. [34,36], is chosen as the candidate science orbit for the CubeSat. For the mothership, a high 100 × 200 km ($A_x\times A_y$) planar QSO, which is safe from escape and impact, is adopted.

3. Budget Analyses and CubeSat Design

3.1. Deployment $\Delta v$ Budget

Owing to the small capacity of the micro-propulsion system, the $\Delta v$ cost for deploying the CubeSat from the orbit of the mothership to the low QSO should be low. Ikeda et al. [37] investigated the $\Delta v$ cost for transfers between QSOs around Phobos and robust injection points in terms of operational safety. They suggested that the injection $\Delta v$ be executed at leading and trailing points (i.e., at the y maximum and minimum in the rotating frame) of the QSOs and the intermediate “swing” QSOs. The swing QSO is the multi-revolution QSO with $A_y$ oscillating in the along-track direction of Phobos’ orbit, and connects low and high periodic QSOs. Figure 3 displays an example of a transfer from the 100 × 200 km QSO to the 29 × 46 km QSO in the Phobos-centered rotating frame with Mars on the $-x$ axis. Note that the purpose here is simply to have an estimate of the deployment $\Delta v$ budget. Trajectories and $\Delta v$ are computed in the simplified CR3BP model. Three impulses are used in this example and all implemented at the leading or trailing points. The transfer is not particularly optimized, while the total $\Delta v$ is an affordable 16 m/s. To inject the CubeSat to the targeted 3D QSO, an out-of-plane $\Delta v$ around 3 m/s is required to incline the orbit. Therefore, the deployment requires a $\Delta v$ approximately at 20 m/s in total. For clear illustration, the shown transfer is the shortest case without revolving around Phobos, which is actually not practical in operation. As Ikeda et al. have noted, since the transfer arcs between QSOs belong to the swing QSOs that keep coming back to the same positions, $\Delta v$ can be implemented after several revolutions (preferably >2 days) to have a sufficiently long arc for orbit determination at an acceptable operation accuracy (for details, see Refs. [37,38]).

3.2. Doppler Measurement and Link Budget

The two-way Doppler setting is selected. In this setting, the signal is generated and emitted by the mothership, then received and transponded by the CubeSat, and finally received and measured by the mothership. The measurement noise consists of the time system noise and the receiver tracking-loop noise. An ultra-stable oscillator (USO) that triggers the radio signals is placed on the mothership. The two-way setting not only simplifies the CubeSat design, but also leads to less time system noise than the one-way setting (i.e., where a less accurate clock is placed on the CubeSat). The thermal noise is related to the received carrier-to-noise density ratio of the radio link, $C/N_0$. To compute $C/N_0$, the link budget should be analyzed. The UHF radio is adopted, which will be explained in the next subsection. The link budget is presented in

Table 1. Link budget.

Item	Symbol	Unit	Value
Frequency	f	MHz	435
Carrier wave length	${\mathsf{\lambda }}_L$	m	0.6892
Transmitter output power	$P_t$	dBW	−3 a
Transmit antenna gain	$G_t$	dB	0 b
Equiv. isotropic radiated power	$EIRP$	dBW	−3
Propagation path length	D	km	250 c
Space loss	$L_s$	dB	−133.18
Receive antenna gain	$G_r$	dBi	0
Received power	C	dB	−136.18
System noise temperature	$T_s$	K	635
Carrier to noise density ratio	$C/N_0$	MHz	2.84

^a ISIS V/U tranceiver. ^b Endurosat UHF antenna. ^c Maximum mothership-CubeSat distance.

(for the steps computing the link budget, refer to Ref. [39]). Other parameters of the Doppler measurement are presented in

Table 2. Doppler noise budget.

Item	Symbol	Unit	Value
Clock stability	${\sigma }_{f_{\mathrm{time}}}/f$	-	$5\times {10}^{-13}$a
Code loop noise bandwidth	$B_n$	Hz	20
Predetection integration time	$t_p$	sec	5
PLL thermal noise	${\sigma }_{f_{\mathit{PLL}}}/f$	-	$2.74\times {10}^{-13}$
Overall measurement noise b	${\sigma }_{v_r}$	mm/s	$8.55\times {10}^{-2}$

^a General Allen stability of a USO. ^b Root-sum-squared of clock and PLL noises.

, where the noise in the PLL tracking loop, ${\sigma }_{f_{PLL}}$ [Hz], is computed from (for details, see Ref. [40])

$${\sigma }_{f_{PLL}}=\frac{\sqrt{2}}{2\pi t_p}\sqrt{\frac{B_n}{C/N_0}\left[1+\frac{1}{2t_{p}C/N_0}\right]}$$

(1)

As summarized in Table 2, the overall Doppler measurement (or range-rate) noise, ${\sigma }_{v_r}$, is around 0.09 mm/s.

3.3. System Sizing

The mission requires constant measurements of Doppler shifts between the mothership and CubeSat via the communication link. However, the limited solar panel area of the CubeSat and the only 51% power generation efficiency, compared to that at 1 AU, constrain the power usage. The UHF radio is adopted in this situation. It allows omni-directional transmission, and thus permits constant Sun pointing for maximum power supply.

Considering these settings, the components and specifications of the CubeSat are decided, as listed in

Table 3. Components, mass, and power budgets of the CubeSat.

Subsystem	Components	Weight, g	Power, W
Structure	1 2U frame	390 a	-
	Shielding and deployable panels	523 a	-
Power	>10 1U solar arrays	440	+12.24 b
	1 battery	258 c	+38.5 h c
ADCS	4 reaction wheels	220 a	−0.8 a
	1 star tracker	170 d	−1.5 d
	1 MEMS IMU	20	−0.6
	Sun sensors	- e	−0.33
Communication	1 UHF antenna set	85 f	−1 f
	1 UHF transceiver	75 g	−4 g
C&DH	1 on-board computer	100	−0.4
Propulsion	1 cold-gas thruster	676 h	−0.25 h
Margin	-	444 i	−1.3 i
Total	-	3401	2.0

^a Based on a lunar CubeSat development experience [41,42]. ^b During the sun-pointing phase with 51% of the efficiency obtained at 1 AU. ^c GOMSpace NanoPower BP4, https://gomspace.com/shop/subsystems/power/nanopower-bp4.aspx, accessed on 19 February 2019. ^d MAI-SS Space Sextant, https://www.cubesatshop.com/wp-content/uploads/2016/06/MAI-SS-Specification-10-11-17.pdf, accessed on 1 February 2021. ^e Attached to solar arrays. ^f EnduroSat UHF antenna, https://www.endurosat.com/cubesat-store/all-cubesat-modules/uhf-antenna/, accessed on 1 February 2021. ^g ISIS V/U tranceiver, https://www.isispace.nl/product/isis-uhf-downlink-vhf-uplink-full-duplex-transceiver/, accessed on 1 February 2021. ^h VACCO End-Mounted Standard MiPS (0.25U) https://www.cubesat-propulsion.com/wp-content/uploads/2015/10/End-mounted-standard-mips.pdf accessed on 1 February 2021. ⁱ Additional 15% to account for thermal control parts, resistors and coating, and margins of subsystem components.

. All components can be accommodated into a 2U configuration, as shown in Figure 4. The power and mass budgets either based on commercial off-the-shelf specifications or CubeSat development experience are also presented in Table 3. With the largest surface, to which 10 1U solar panels are attached, constantly pointed to the Sun, power generation can cover the consumption during the operating mode. Given a CubeSat dry mass of 2.62 kg, the VACCO 0.25U cold-gas thruster with a total impulse of 93 N·s, specific impulse of 40 s, and wet mass of 676 g can deliver a total $\Delta v$ of 29 m/s, which covers the need of the deployment, 20 m/s. The total mass of 3.4 kg and volume of 2U should not impose significant loads to the launcher and the mothership. There is still some spare space in the current design. Even 3U and 6U configurations, which are adopted by the CubeSats MarCo [24], Juventas [25], and Milani [26] boarding an interplanetary mothership, are also considered practical. Therefore, depending on the mass and volume budgets allocated to the piggyback, more parts and propulsion capacity may be added to this lowest-cost and most-simplified baseline design, to enhance the robustness and flexibility of the CubeSat mission.

4. Models of Geodesy and Orbit Determination

4.1. Baseline Model

The dynamic model, as well as the developed orbit propagator, considers ephemerides and gravity of the Sun, Mars, and Phobos. The mar097 ephemeris developed at JPL [43] is adopted as the true ephemeris of Mars and Phobos. The Mars spherical harmonics gravity model is considered up to 10 degrees and orders, whose values are available from the JPL model jgmro_110b. The used Phobos gravity model is up to 3 degrees and orders. The baseline gravity harmonics coefficients of Phobos are computed by the CNES Geodesy Group based on Gaskell’s Phobos shape model [44] under the assumption of homogeneous density and $GM$ of $7.1\times {10}^{-4}$ km${}^3$/s${}^2$.

The rotational model is computed by Rambaux et al. [45] under the homogeneous assumption, which is expressed as:

$$\begin{array}{ccc}\hfill \alpha & =& 317.652+1.789sin({\mu }_{1}d+169.521),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \delta & =& 52.875-1.078cos({\mu }_{1}d+169.521),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill W\hfill & =& 34.781+{\mu }_{3}d+1.27{10}^{-3}{t}^2\hfill \\ & & -1.427sin({\mu }_{1}d+169.521)-1.100sin({\mu }_{2}d+189.271),\hfill \end{array}$$

(4)

where $\alpha$ [${}^{\circ }$] denotes the right ascension of the figure axis of Phobos, $\delta$ [${}^{\circ }$] the inclination of its equatorial plane, and W [${}^{\circ }$] the proper rotation (i.e., $\alpha$-$\delta$-W forms a 3-1-3 rotation sequence with respect to the J2000 ecliptic frame); in addition, d is the integer part of the Julian day, and t is the elapsed seconds on that day. The values of ${\mu }_1$, ${\mu }_2$, ${\mu }_3$ are

$$\begin{array}{ccc}\hfill {\mu }_1& =& -0.4357344031969911\hfill \\ \hfill {\mu }_2& =& 1128.409666972337\hfill \\ \hfill {\mu }_3& =& 1128.844884999715\hfill \end{array}$$

The baseline libration amplitude $\theta$ [${}^{\circ }$] is −1.1${}^{\circ }$ in Equation (4).

Considering the limited power capacity of the CubeSat, the geodesy campaign should take place during an eclipse-free season. One eclipse-free season is from March 2026 to June 2026 [46]. This period is promising for the Martian mission launched in the year 2024. In the simulation, the initial epoch is set to 2026-4-1 12:00 UTC. As the time of flight of the deployment trajectory is variable, as explained in Section 3.1, and there is no particular requirement on the initial phases of the two orbits, it is assumed that both probes start at the periapsis on the anti-Mars side (i.e., at the x maximum on the x-axis in the rotating frame). Figure 5 presents the evolution of science orbits of the mothership and CubeSat for one week in the described dynamic model. The candidate orbits stay bounded without escape or impact in the high-fidelity model. The Doppler measurement is taken at 1-min intervals. Note that the occultation of Phobos is also considered. In other words, measurements are not valid when Phobos blocks the link. Valid measurements during one week are processed by the estimation routine. In summary, the true orbits of the spacecraft are propagated from true initial orbit states in the high-fidelity dynamic model with the baseline geodetic parameters of Phobos and the mar097 ephemeris, and true range-rates at measurement epochs are generated.

4.2. Error Models

To reveal the influence of ephemeris errors, in the estimation simulation, the mar097 and the NOE-4-2020 developed at IMCCE [47] are adopted as the known ephemerides to express the situations without and with ephemeris errors, respectively. The difference between mar097 and NOE-4-2020 during the period from 2025 to 2027 is around 2 km, mainly along the transverse direction (for more details, see Ref. [47]). The ephemeris error can be approximated by and regarded as a phase shift, $\Delta et$, of 0.9 s.

According to the result obtained by Jacboson and Lainey [11], the non-spherical gravity coefficients of Phobos under the homogeneous assumption can be within a 10% difference from the true situations. The a priori uncertainty of these parameters is set to 10%, and that of $GM$ is set to 3% in this work. Because of the small uncertainty or the small influence, Martian gravity coefficients and parameters other than libration amplitude in Equations (2)–(4) are fixed in the analysis. The a priori uncertainties of the initial orbit states are set to 100 m on each position component and 10 cm/s on each velocity component, which is much greater than the presumed uncertainty of ground-based orbit determination. The Doppler measurement noise ${\sigma }_{v_r}$, as analyzed in Section 3.2, is conservatively set to 0.1 mm/s. In the Monte Carlo simulation presented in Section 5.3, random errors are generated according to these assumed uncertainties.

Table 4. Summary of error items.

Item	A Priori Uncertainty
Range-rate measurement	0.1 mm/s
Spacecraft position	(100, 100, 100) m
Spacecraft velocity	(10, 10, 10) cm/s
Phobos’ $C_{00}$	3%
Non-spherical CS coefficients	10%
Libration amplitude $\theta$	0.11${}^{\circ }$
Ephemeris error (if present)	$\left|\mathtt{NOE}-\mathtt{4}-\mathtt{2020}-\mathtt{mar}\mathtt{097}\right|$

summarizes the uncertainties in the model and measurements. Note that a priori covariances between each of the two uncertain variables are set to zero.

4.3. Theoretical Covariance

The general estimation algorithm optimizes the likelihood of the estimate based on the a priori or predicted covariance and the measurement pre-fit residuals. The a posteriori covariance of estimated variables can be expressed as:

$${\mathbf{P}}^{*}={\mathbf{P}}_0-{\mathbf{P}}^{e_x{e}_y}{{\mathbf{P}}^{e_y{e}_y}}^{-1}{{\mathbf{P}}^{e_x{e}_y}}^{\mathrm{T}},$$

(5)

where ${\mathbf{P}}^{e_x{e}_y}$ ($\in {\mathbb{R}}^{n\times N}$) represents the cross-correlation matrix mapping n uncertain variables $\mathbf{X}$ ($\in {\mathbb{R}}^{n\times 1}$) (i.e., including initial orbit states of mothership and CubeSat, Phobos’ geodetic parameters, and ephemeris errors) to the range-rate measurements $\mathbf{Y}={\left[v_{r1}\dots v_{rN}\right]}^{\mathrm{T}}$ ($\in {\mathbb{R}}^{N\times 1}$) obtained at a series of N epochs. ${\mathbf{P}}_0$ ($\in {\mathbb{R}}^{n\times n}$) is the a priori covariance matrix, where the diagonal elements are the squares of values presented in Table 4. ${\mathbf{P}}^{e_y{e}_y}$ represents the innovation covariance expressed as:

$${\mathbf{P}}^{e_y{e}_y}={\mathbf{P}}^{yy}+{\mathbf{R}}^v,$$

(6)

where ${\mathbf{P}}^{yy}$ ($\in {\mathbb{R}}^{N\times N}$) represents the output covariance matrix and ${\mathbf{R}}^v$ ($\in {\mathbb{R}}^{N\times N}$) the covariance of measurement error. ${\mathbf{R}}^v$ is a diagonal matrix with ${{\sigma }_{v_r}}^2$ in the diagonal entries. ${\mathbf{P}}^{e_x{e}_y}$ and ${\mathbf{P}}^{yy}$ can be obtained using unscented transforms (for details, see Ref. [48]).

The estimation accuracies in two situations, one without ephemeris error and another one under ephemeris errors, are investigated. In this analysis, the mapping from the uncertain ephemeris error to $\mathbf{Y}$ is approximated by the mapping from the ephemeris time shift $\Delta et$. The theoretical estimation accuracy ${\mathbf{P}}^{*}$ achieved in one week is computed from Equation (5). The resulting relative uncertainty is presented in Figure 6. Note that, to show the relative uncertainties of the zero parameters, $C_{10}$, $C_{11}$, and $S11$, ${10}^{-5}$ is adopted to represent their reference values. As is shown, the accuracies of $C_{20}$, $C_{22}$, and libration amplitude, $\theta$, under the ephemeris error are as small as 0.04‰, 0.2‰, and 1‰, respectively. Nevertheless, as the estimation problem involves many uncertain variables and is highly-nonlinear, in practice, the numerical algorithm may not achieve this theoretical accuracy.

5. Numerical Estimation Simulations

This section presents the practical accuracies of Phobos geodesy and spacecraft orbit determination. Random errors are generated based on the a priori uncertainty described in Table 4 and added to the baseline values. Considering 29 uncertain variables (i.e., $6\times 2$ orbit states, $3\times 3$ CS coefficients, and 1 libration amplitude) and the long computation time to run one estimation routine, $29\times 10$ errored samples of the variables are generated as the initial guesses for estimation simulations. Another uncertain factor exists, the ephemeris error. Two situations are simulated, one without ephemeris error in the environment, and the other with ephemeris errors present. The statistical pattern of the covariance is elucidated by Monte-Carlo simulations, as presented in Section 5.3.

Regarding the estimation routine, it is usually difficult to recover both orbit states and geodetic parameters simultaneously. Two scenarios, online orbit determination and offline parameter identification, are planned. The online estimation processes the new measurement to update spacecraft orbit states and the $C_{00}$ of Phobos using the sequential unscented Kalman filter. In the offline scenario, the batch filter is used to smooth previous estimates and recover the rest of uncertain variables (details of estimation routines will be presented in Ref. [49]).

5.1. Orbit Determination

This subsection presents the estimation process for one sample of initial guesses, exhibiting the impact of ephemeris error, and the effect of mitigating this impact. The adopted sampled initial guesses and baseline values (i.e., the assumed true values) are listed in

Table 5. Presumed truth values and one sample of initial knowledge.

Item	Truth	Initial Knowledge
$x_c$ [km]	−16.361	−16.387
$y_c$ [km]	−10.789	−10.745
$z_c$ [km]	30.088	30.128
$v_{cx}$ [m/s]	1.213	1.088
$v_{cy}$ [m/s]	7.249	7.154
$v_{cz}$ [m/s]	3.119	3.045
$x_m$ [km]	−88.829	−88.880
$y_m$ [km]	−6.438	−6.470
$z_m$ [km]	46.460	46.462
$v_{mx}$ [m/s]	3.592	3.289
$v_{my}$ [m/s]	20.561	20.515
$v_{mz}$ [m/s]	9.009	9.133
${\overline{C}}_{00}$	1.00000	0.995321
${\overline{C}}_{20}$ *	−0.04757	−0.05173
${\overline{C}}_{21}$	0.00127	0.00123
${\overline{C}}_{22}$	0.02467	0.02863
${\overline{S}}_{21}$	0.00014	0.00014
${\overline{S}}_{22}$	0.00032	0.00029
${\overline{C}}_{30}$	0.00303	0.00288
${\overline{C}}_{31}$	−0.00452	−0.00464
${\overline{C}}_{32}$	−0.00902	−0.00923
${\overline{C}}_{33}$	0.00162	0.00154
${\overline{S}}_{31}$	0.00216	0.00249
${\overline{S}}_{32}$	0.00075	0.00084
${\overline{S}}_{33}$	−0.01360	−0.01565
$\theta$ [${}^{\circ }$]	−1.1000	−1.1276

* CS coefficients are normalized values.

for comparison. Note that the a priori and initial guesses of $C_{10}$, $C_{11}$, and $S_{11}$ are set to zero. The process of on-board autonomous navigation (or online orbit determination) under no ephemeris error (i.e., the mar097 ephemeris is employed in the estimation routine) is displayed in Figure 7. The estimation process converges and starts to follow new orbit states in one day. Upon convergence, the average root-sum-squared (RSS) position uncertainty is around 0.2 m, and the RSS velocity uncertainty is 0.05 mm/s. Figure 8 shows the process of online estimation in the presence of ephemeris errors (i.e., the ephemeris NOE-4-2020 is used). The RSS position uncertainty is significantly increased to 81.6 m, and the RSS velocity uncertainty to 1.63 cm/s. Considering the influence of ephemeris error on the estimation, an ephemeris time error $\Delta et$ is taken as a consider parameter [49]. Figure 9 shows the estimation process considering the ephemeris time error. The RSS position uncertainty is substantially improved to 20.7 m, and the RSS velocity uncertainty to 0.4 cm/s.

Discussion on Orbiting Operations

The obtained accuracy is substantially better than that of the presumed ground-based orbit determination. Moreover, as the convergence time is 1 day, the proposed mission can also support rapid orbit changes independent from ground stations (i.e., without Earth pointing operations nor waiting tens of minutes for commands to travel). As a reference, the permitted orbit maneuver interval in the MMX mission is 2 days, which is associated with the ground-based orbit determination method [38]. Therefore, the proposed orbit determination approach enjoys advances in accuracy, speed, and autonomy.

In addition, for certain mission requirements, the mothership and CubeSat can switch their orbits. For instance, the CubeSat can be first deployed in the low QSO to perform Phobos geodesy, and then deployed to a high QSO serving as a beacon to support the proximity orbiting operation performed by the mothership in a low QSO thereafter. In this case, a bigger cold-gas thruster is required. As reasoned in Section 3.3, slightly bigger configurations are acceptable from a practical perspective. For example, a 0.5U thruster in a 2U CubeSat configuration can deliver a total $\Delta v$ of 49 m/s, and a 0.8U thruster in a 3U CubeSat configuration can deliver a total $\Delta v$ of 68 m/s, which can meet the additional requirement of deployment to a high QSO.

5.2. Parameter Identification

The errors of gravity coefficients estimated in the three situations are shown in Figure 10. It can be seen that the ephemeris error significantly interrupts parameter identification. In particular, the libration amplitude $\theta$ cannot be estimated if the ephemeris error is present and not considered in the estimation. With the ephemeris error considered in the estimation, its impact on parameter identification is significantly reduced.

5.3. Statistical Covariance

The Monte-Carlo simulation is performed to derive a statistical conclusion. Two situations are considered. One situation is without ephemeris error. Tho other is under ephemeris errors, and the ephemeris error is considered in the estimation. For each situation, 290 simulations starting with the 290 errored samples of uncertain variables are run. Statistical covariance of the gravity coefficients is concluded from differences of the estimates from the true values. The obtained standard deviation is presented in

Table 6. Standard deviation of estimated gravity coefficients elucidated by the Monte-Carlo simulation.

Item	Absence of Ephemeris Errors	Presence of Ephemeris Errors
$C_{00}$	$2.5\times {10}^{-7}$	0.08‰
$C_{20}$	0.04‰	0.65‰
$C_{22}$	0.15‰	1.88‰
$\theta$	0.59‰	8.32%

. The impact of ephemeris errors on geodesy is clearly observed from the differences. Nevertheless, even in the presence of the ephemeris error of 2 km, by considering an ephemeris time error in the estimation, the uncertainty of $C_{00}$ can be kept down to 0.08‰, which is better than the latest implications (e.g., 0.3%, [10]; 0.04%, [15]) from flyby tracking data, suggesting an advanced effectiveness of the proposed dual-sat radiometric observation. The influence of ephemeris error on 2nd-degree gravity identification is around 0.6‰ for $C_{20}$ and 1.7‰ for $C_{22}$. The 1-$\sigma$ uncertainties of $C_{20}$ and $C_{22}$ are hundreds of times smaller than that derived from past flyby tracking data (i.e., 8% and 30%, [15]). The libration amplitude $\theta$, however, becomes almost unobservable under the ephemeris error, as the obtained accuracy is just slightly better that the a priori, 10%. Errors of $C_{20}$ and $C_{22}$ are plotted in Figure 11, along with the concluded covariance ellipses.

Uncertainties of recovered variables are added to Figure 6 for a clear comparison with the theoretical uncertainties. It can be seen that, the trend of the practical uncertainities generally follows that of the theoretical. While the practical uncertainties are generally greater than the theoretical, the differences are modest. This certifies that estimation routine functions correctly. The difference between the practical and theoretical uncertainties can be related to the non-linearity of the dynamics and the large number of estimated variables. The difference is greater in the situation with ephemeris errors, owing to the unmodeled ephemeris errors in cross-track and radial directions.

6. Effect of Inferring Interior Structure

$C_{20}$ and $C_{22}$ are related to the MoI of the target. Let $I_{xx}$, $I_{yy}$, and $I_{zz}$ represent the principle MoI, M the mass, and $R_0$ the reference radius of Phobos. Then, let A, B, and C represent the normalized MoI, $I_{xx}/\left(M{R}_0^2\right)$, $I_{yy}/\left(M{R}_0^2\right)$, and $I_{zz}/\left(M{R}_0^2\right)$, respectively. The relationship between 2nd-degree gravity coefficients and MoI is expressed as:

$$\begin{array}{cc}\hfill C_{22}& =(B-A)/4,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill C_{20}+2C_{22}& =B-C.\hfill \end{array}$$

(8)

The libration amplitude $\theta$ [rad] is in related to the flatting $\gamma =(B-A)/C$, which is expressed as [50]:

$$\theta =\frac{2e}{1-\frac{1}{3\gamma }},$$

(9)

where $e=0.01511$ is the orbital eccentricity of Phobos. Equations (7)–(9) can be rewritten as:

$$\begin{array}{cccc}\hfill A& =C_{20}\hfill & \hfill +& (10-24e/\theta )C_{22},\hfill \end{array}$$

(10)

$$\begin{array}{cccc}\hfill B& =C_{20}\hfill & \hfill +& (14-24e/\theta )C_{22},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill C& =\hspace{1em}\hspace{1em}\hspace{1em}\hfill & (12-24e/\theta )C_{22}.\hfill \end{array}$$

(12)

Accordingly, the baseline MoIs are $A=0.3537$, $B=0.4174$, and $C=0.4919$.

The small error of $GM$ is negligible in influencing the MoI. To relate errors of $C_{20}$, $C_{22}$, and $\theta$ to errors of MoI, differential equations are derived as follows,

$$\left[\begin{array}{c}\partial A\\ \partial B\\ \partial C\end{array}\right]=\left[\begin{array}{ccc}1& 10-24e/\phantom{24e\theta }\theta & 24e{C}_{22}/\phantom{24e{C}_{22}{\theta }^2}{\theta }^2\\ 1& 14-24e/\phantom{24e\theta }\theta & 24e{C}_{22}/\phantom{24e{C}_{22}{\theta }^2}{\theta }^2\\ 0& 12-24e/\phantom{24e\theta }\theta & 24e{C}_{22}/\phantom{24e{C}_{22}{\theta }^2}{\theta }^2\end{array}\right]\left[\begin{array}{c}\partial C_{20}\\ \partial C_{22}\\ \partial \theta \end{array}\right].$$

(13)

The Jacobian matrix in Equation (13) indicates that $C_{22}$ and $\theta$ are three to four times more influential than $C_{00}$ at the same level of relative error, given the baseline values of the parameters. Let $\mathbf{M}$ represent the Jacobian matrix. The covariance of the MoI variables on the left-hand side, ${\mathbf{P}}_{\mathbf{I}}$, is related to the covariance of the parameters on the right-hand side, ${\mathbf{P}}_{\mathbf{P}}$ as:

$${\mathbf{P}}_{\mathbf{I}}=\mathbf{M}{\mathbf{P}}_{\mathbf{P}}{\mathbf{M}}^{\mathrm{T}}.$$

(14)

The previous subsection has deduced ${\mathbf{P}}_{\mathbf{P}}$ from the statistical result. The covariance of MoI is computed from Equation (14) and depicted in Figure 12. When there is no ephemeris error, the accuracy of MoI is as good as $3.3\times {10}^{-4}$ (i.e., 0.9‰). When the ephemeris error is present, the 1-$\sigma$ uncertainty of each normalized MoI is around 0.04 (i.e., 10%), mainly contributed by the $\theta$ error. This resolution of MoI cannot directly distinguish families of the interior structure. However, according to Le Maistre et al. [9], the MoI distributions of heavily-fractured and porous-compressed families behave in an opposite way (for details, see Figure 8 of Ref. [9]). Therefore, the near-proportional error distribution exhibited in Figure 12 can distinguish these two families of interior structures.

Le Maistre et al. [9] also computed the distribution of different structure families over $C_{20}$ and $C_{22}$. The uncertainty ellipse in Figure 11 is placed on the distribution map from Ref. [9], which is shown in Figure 13. Because of the comparably tiny sizes of the uncertainties obtained in this work, only the 3-$\sigma$ uncertainty ellipse under ephemeris errors is shown. Errors of the estimated $C_{20}$ and $C_{22}$ are constrained in this ellipse for the ephemeris error up to 2 km. Given this comparably tiny margin, we can separate the possibility of heavily fractured, porous compressed, and the families in the middle of the map, and distinguish the disrupted-and-reaccreted family from the icy-surface-concentrated and rubble-pile families, regardless of the true values of the parameters.

7. Conclusions

A mothership-CubeSat radioscience mission was proposed to probe Phobos and support autonomous navigation. The two probes are placed in a high (e.g., $100\times 200$ km) quasi-satellite orbit (QSO) and a low three-dimensional (e.g., $29\times 30\times 21$ km) QSO about Phobos, respectively. The operation plan and system design were given to meet requirements of power, deployment $\Delta v$, and Doppler measurement. The presented analysis of geodesy and orbit determination takes into account errors in the measurements and model, including the ephemeris error. Practically achievable estimation uncertainty was revealed via the Monte-Carlo simulation. The moderate difference between the practical and theoretical uncertainties suggests the functionality of the estimation algorithm and the need for verification via the statistical numerical analysis.

Evident impacts of ephemeris errors on orbit determination and geodesy were observed. Nevertheless, these impacts were substantially reduced by considering the ephemeris error in the estimation. The RSS orbit uncertainties under no ephemeris error are 0.2 m and 0.05 mm/s. The uncertainties increase to 21 m and 0.4 cm/s when an ephemeris error of approximately 2 km is present. This accuracy is still better than the presumed accuracy of ground-based orbit determination (i.e., RSS 86 m and 0.5 cm/s). Thus, the proposed approach can support autonomous orbit determination and rapid (i.e., <1 day) orbit maneuvers in the proximity of the target, and can tolerate ephemeris errors up to a few kilometers.

Even under the ephemeris error, the uncertainties of $C_{20}$ and $C_{22}$ recovered from the proposed mission are as small as 0.7‰ and 1.9‰, respectively. However, the a posteriori uncertainty of libration amplitude, 8.3%, is not significantly improved from the a priori, 10%. This uncertainty contributes to an uncertainty of 10% in the moment of inertia of Phobos. As the identification of libration is susceptible to the ephemeris error, for high precision of the libration amplitude and the moment of inertia, it is recommended to update the ephemeris of Phobos before the radioscience campaign. Uncertainties achieved in this work are so far the lowest among values obtained in past radioscience campaigns and future mission concepts verified in high-fidelity simulations. The obtained covariance of geodetic parameters can distinguish the porous-compressed interior structure from the heavily-fractured family, and the disrupted-and-reaccreted one from the icy-surface-concentrated and rubble-pile families, regardless of the true values of the parameters.