SGOT: A Simplified Geometric-Optical Model for Crown Scene Components Modeling over Rugged Terrain
Abstract
:1. Introduction
2. SGOT Model Development
2.1. Crown Shape Transformations
2.2. Projection of Tree Crowns over Sloping Surfaces
2.3. Crown Gap Fraction over Sloping Surfaces
2.4. Areal Proportions of Scene Components over Sloping Surfaces
3. Experimental Setting and Design
3.1. Strategy for Evaluating the Performance of the SGOT Model
3.2. Simulation of Scene Components with Computer 3-D Virtual Model
3.3. Input Parameter Settings of Each Compared GO-like Model
4. Results and Analysis
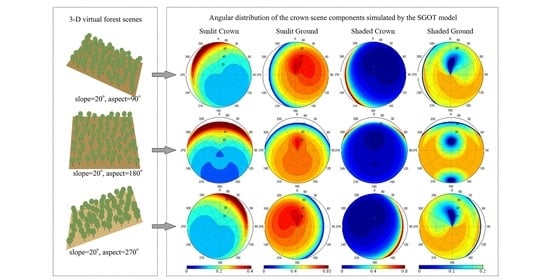
4.1. SGOT Model Validation through 3-D Virtual Canopy Model Simulations
4.2. Analysis of Topographic Effects on Scene Components by SGOT Modeling
4.3. Comparison with Typical GO-Like Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Projection Algorithm of Tree Crowns of Various Shapes on Sloping Surface
References
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Ross, J. The radiation regime and architecture of plant stands. J. Ecol. 1981, 71, 344. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 705–721. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Li, X.; Woodcock, C.; Davis, R. A hybrid heometric optical and radiative transfer approach for modeling pyranometer measurements under a jack pine forest. Geogr. Inf. Sci. 1995, 1, 34–40. [Google Scholar]
- Huemmrich, K.F. The geosail model: A simple addition to the SAIL model to describe discontinuous canopy reflectance. Remote Sens. Environ. 2001, 75, 423–431. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Martin, E.; Gascon, F. DART: A 3D model for simulating satellite images and studying surface radiation budget. Int. J. Remote Sens. 2004, 25, 73–96. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Xu, Y.; Yan, G. Principles and applications of the 3D radiative transfer model LESS. Remote Sens. Technol. Appl. 2019, 34, 914–924. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Gu, D.; Gillespie, A. Topographic normalization of Landsat TM images of forest based on subpixel sun-canopy-sensor geometry. Remote Sens. Environ. 1998, 64, 166–175. [Google Scholar] [CrossRef]
- Li, A.; Wang, Q.; Bian, J.; Lei, G. An improved physics-based model for topographic correction of Landsat TM images. Remote Sens. 2015, 7, 6296–6319. [Google Scholar] [CrossRef] [Green Version]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A modified sun-canopy-sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Wu, S.; Fan, W.; Zeng, Y.; Kai, Y.; Xu, B.; Jing, L.; Liu, Q. Plc: A simple and semi-physical topographic correction method for vegetation canopies based on path length correction. Remote Sens. Environ. 2018, 215, 184–198. [Google Scholar] [CrossRef]
- Proy, C.; Tanre, D.; Deschamps, P.Y. Evaluation of topographic effects in remotely sensed data. Remote Sens. Environ. 1989, 30, 21–32. [Google Scholar] [CrossRef]
- Sandmeier, S.; Itten, K. A physically-based model to correct atmospheric and illumination effects in optical satellite data of rugged terrain. IEEE Trans. Geosci. Remote Sens. 1997, 35, 708–717. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.; Chen, J.M.; Ju, W.; Zhu, G. Gost: A geometric-optical model for sloping terrains. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5469–5482. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Zhao, W.; Jin, H.; Bian, J.; Wu, S. Modeling canopy reflectance over sloping terrain based on path length correction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4597–4609. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M. Improved LAI algorithm implementation to MODIS data by incorporating background, topography, and foliage clumping information. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1076–1088. [Google Scholar] [CrossRef]
- Pasolli, L.; Asam, S.; Castelli, M.; Bruzzone, L.; Wohlfahrt, G.; Zebisch, M.; Notarnicola, C. Retrieval of leaf area index in mountain grasslands in the Alps from MODIS satellite imagery. Remote Sens. Environ. 2015, 165, 159–174. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil–leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Li, X.; Strahler, A.H. Topographic effects on bidirectional and hemispherical reflectances calculated with a geometric-optical canopy model. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1186–1193. [Google Scholar] [CrossRef]
- Fan, W.; Li, J.; Liu, Q. Gost2: The improvement of the canopy reflectance model gost in separating the sunlit and shaded leaves. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1423–1431. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; North, P.R.J. Monte carlo ray tracing in optical canopy reflectance modelling. Int. J. Remote Sens. 2000, 18, 163–196. [Google Scholar] [CrossRef]
- Omari, K.; White, H.P.; Staenz, K. Multiple scattering within the flair model incorporating the photon recollision probability approach. Geosci. Remote Sens. IEEE Trans. 2009, 47, 2931–2941. [Google Scholar] [CrossRef]
- Wu, S.; Wen, J.; Lin, X.; Hao, D.; You, D.; Xiao, Q.; Liu, Q.; Yin, T. Modeling discrete forest anisotropic reflectance over a sloped surface with an extended GOMS and SAIL model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 944–957. [Google Scholar] [CrossRef]
- Combal, B.; Isaka, H.; Trotter, C. Extending a turbid medium BRDF model to allow sloping terrain with a vertical plant stand. IEEE Trans. Geosci. Remote Sens. 2000, 38, 798–810. [Google Scholar] [CrossRef]
- Geng, J.; Chen, J.; Fan, W.; Tu, L.; Tian, Q.; Yang, R.; Yang, Y.; Wang, L.; Lv, C.; Wu, S. Gofp: A geometric-optical model for forest plantations. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5230–5241. [Google Scholar] [CrossRef]
- Yin, G.; Li, J.; Liu, Q.; Fan, W.; Xu, B.; Zeng, Y.; Zhao, J. Regional leaf area index retrieval based on remote sensing: The role of radiative transfer model selection. Remote Sens. 2015, 7, 4604–4625. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Strahler, A. Mutual shadowing and directional reflectance of a rough surface—A geometric-optical model. In Proceedings of the 12th Annual International Geoscience and Remote Sensing Symposium, Houston, TX, USA, 26–29 May 1992; Volume 1, pp. 766–768. [Google Scholar]
- Montes, F.; Pita, P.; Rubio, A.; Cañellas, I. Leaf area index estimation in mountain even-aged Pinus silvestris L. Stands from hemispherical photographs. Conf. Agric. For. Meteorol. 2007, 145, 215–228. [Google Scholar] [CrossRef]
- Alijafar, M.; Wout, V.; Massimo, M.; Ben, G. Modeling top of atmosphere radiance over heterogeneous non-lambertian rugged terrain. Remote Sens. 2015, 7, 8019–8044. [Google Scholar] [CrossRef] [Green Version]
- Norman, J.M.; Welles, J.M. Radiative transfer in an array of canopies. Agron. J. 1983, 75, 481–488. [Google Scholar] [CrossRef]
- Strahler, A.H.; Jupp, D.L.B. Modeling bidirectional reflectance of forests and woodlands using boolean models and geometric optics. Remote Sens. Environ. 1990, 34, 153–166. [Google Scholar] [CrossRef]
- Sinoquet, H.; Thanisawanyangkura, S.; Mabrouk, H.; Kasemsap, P. Characterization of the light environment in canopies using 3D digitising and image processing. Ann. Bot. 1998, 82, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Kuusk, A. The Hot Spot Effect in Plant Canopy Reflectance; Springer: Berlin/Heidelberg, Germany, 1991; pp. 139–159. [Google Scholar]
- Wang, J.; Feng, Z.; Hu, L.I.; Tao, Y.U.; Xingfa, G.U.; Lian, X. Sunlit coponents’ fractions and gap fraction of canopies based on POV-ray. Remote Sens. 2010, 14, 232–251. [Google Scholar] [CrossRef]
- Shang, H.; Zhao, F.; Zhao, H. The analysis of errors for field experiment based on POV-ray. In Proceedings of the Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4805–4808. [Google Scholar]
- Casa, R.; Jones, H.G. LAI retrieval from multiangular image classification and inversion of a ray tracing model. Remote Sens. Environ. 2005, 98, 414–428. [Google Scholar] [CrossRef]
- Simic, A.; Chen, J.M.; Freemantle, J.R.; Miller, J.R.; Pisek, J. Improving clumping and LAI algorithms based on multiangle airborne imagery and ground measurements. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1742–1759. [Google Scholar] [CrossRef]
- Neyman, J. On a new class of contagious distributions, applicable in entomology and bacteriology. Ann. Math. Stat. 1939, 10, 35–57. [Google Scholar] [CrossRef]
- Rautiainen, M.; Stenberg, P.; Nilson, T.; Kuusk, A. The effect of crown shape on the reflectance of coniferous stands. Remote Sens. Environ. 2004, 89, 41–52. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Huete, A.; Yin, G.; Xu, B.; Fan, W.; Zhao, J.; Yan, K.; Mu, X. A radiative transfer model for heterogeneous agro-forestry scenarios. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4613–4628. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Malenovský, Z.; Clevers, J.G.P.W. Effects of woody elements on simulated canopy reflectance: Implications for forest chlorophyll content retrieval. Remote Sens. Environ. 2010, 114, 647–656. [Google Scholar] [CrossRef] [Green Version]
- Asner, G. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Tian, S.; Zheng, G.; Eitel, J.; Zhang, Q. A lidar-based 3-D photosynthetically active radiation model reveals the spatiotemporal variations of forest sunlit and shaded leaves. Remote Sens. 2021, 13, 1002. [Google Scholar] [CrossRef]
- Wen, J.; Liu, Q.; Liu, Q.; Xiao, Q.; Li, X. Scale effect and scale correction of land-surface albedo in rugged terrain. Int. J. Remote Sens. Int. J. Remote Sens. 2009, 30, 5397–5420. [Google Scholar] [CrossRef]
- Roupioz, L.; Nerry, F.; Jia, L.; Menenti, M. Improved surface reflectance from remote sensing data with sub-pixel topographic information. Remote Sens. 2014, 6, 10356–10374. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Liu, Q.; Xiao, Q.; Liu, Q.; You, D.; Hao, D.; Wu, S.; Lin, X. Characterizing land surface anisotropic reflectance over rugged terrain: A review of concepts and recent developments. Remote Sens. 2018, 10, 370. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Wen, J.; Xiao, Q.; Wu, S.; Hao, D.; Liu, Q. Extending the GOSAILT model to simulate sparse woodland bi-directional reflectance with soil reflectance anisotropy consideration. Remote Sens. 2022, 14, 1001. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.M.; Ju, W.; Nesbitt, N. Hybrid geometric optical–radiative transfer model suitable for forests on slopes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5579–5586. [Google Scholar] [CrossRef]
- Soenen, S.; Peddle, D.; Hall, R.J.; Coburn, C.; Hall, F. Estimating aboveground forest biomass from canopy reflectance model inversion in mountainous terrain. Remote Sens. Environ. 2010, 114, 1325–1337. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Leblanc, S.G.; Lacaze, R.; Roujean, J.-L. Multi-angular optical remote sensing for assessing vegetation structure and carbon absorption. Remote Sens. Environ. 2003, 84, 516–525. [Google Scholar] [CrossRef]













| Parameters | Value/Range |
|---|---|
| Canopy density | 0.2, 0.5, 0.8 |
| Number of crowns | 55, 138, 220 |
| Crown center height (m) | 5 |
| Crown vertical axis (m) | 3.4 |
| Crown horizontal axis (m) | 4.5 |
| Leaf Area Index (m2/m2) | 1, 2.5, 4 |
| Solar zenith angle (°) | 20 |
| Solar azimuth angle (°) | 0 |
| View zenith angle (°) | 0~80 |
| View azimuth angle (°) | 0~360 |
| Slope (°) | 0~60 |
| Aspect (°) | 0, 90, 180, 270 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Li, A. SGOT: A Simplified Geometric-Optical Model for Crown Scene Components Modeling over Rugged Terrain. Remote Sens. 2022, 14, 1821. https://doi.org/10.3390/rs14081821
Hu G, Li A. SGOT: A Simplified Geometric-Optical Model for Crown Scene Components Modeling over Rugged Terrain. Remote Sensing. 2022; 14(8):1821. https://doi.org/10.3390/rs14081821
Chicago/Turabian StyleHu, Guyue, and Ainong Li. 2022. "SGOT: A Simplified Geometric-Optical Model for Crown Scene Components Modeling over Rugged Terrain" Remote Sensing 14, no. 8: 1821. https://doi.org/10.3390/rs14081821
APA StyleHu, G., & Li, A. (2022). SGOT: A Simplified Geometric-Optical Model for Crown Scene Components Modeling over Rugged Terrain. Remote Sensing, 14(8), 1821. https://doi.org/10.3390/rs14081821