1. Introduction
Change detection using remote sensing technology is a valuable research technique in the field of Earth observation [
1,
2,
3]. It quantitatively analyzes multi-temporal images of the same geographical area to determine surface change characteristics [
4].
The needs and standards in the field of communication are increasing [
5,
6] in response to the expanding range of human trajectories. The proposed integrated space–air–ground network has the potential to greatly enhance the efficiency of acquiring various types of information data and improve the computational efficiency of such data [
7,
8]. Incorporating edge computing tasks can improve the overall availability and scalability of the system [
9,
10,
11]. By combining edge computing technology with remote sensing and satellite communication networks, the quality of satellite communication can be improved and the processing capability of satellite tasks can be enhanced, all while ensuring efficient resource scheduling [
12,
13]. Overall, the proposed integrated space–air–ground network has the potential to greatly influence the efficiency of acquiring various types of information data as well as the computational efficiency of such data.
The rich remote sensing data acquired by airborne remote sensing satellites can be used to describe urban land use, cover types and their detailed changes over time [
2,
14,
15]. The field of remote sensing image change detection mostly utilizes a single optical image data source as the research target [
16]. However, the imaging quality of optical remote sensing images is highly susceptible to complex weather, as well as satellite performance. Synthetic-aperture radar (SAR) images contain richer pixel information and clearer detailed information, which can effectively improve the limitations of optical image-based methods in the field of remote sensing change detection. SAR is an active microwave remote sensing technique [
17,
18] that could operate in less restricted natural environments [
19] and plays an important role in remote sensing. The remote sensing change-detection method based on SAR images demonstrates significant advantages in the integrated space–air–ground tasks, such as urban building change detection [
20], forest fire location [
21], and geological disaster monitoring [
22,
23,
24].
Currently, the predominant techniques of image change detection are based on difference-image detection [
25], which involves analyzing the difference images generated from simultaneous phase images to obtain the final binary change maps [
26]. Recently, deep learning has been applied to remote sensing image change detection, with the aim of learning complex features by constructing multilayer network models and training on huge amounts of data [
27,
28,
29,
30]. How to handle deep-level change information [
31] is one of the key challenges in applying deep learning to change detection in the field of remote sensing imagery.
Taking advantage of the powerful feature-capture capability of the convolutional neural network (CNN) [
32,
33,
34], Chen [
28] proposed DSMS-CN and DSMSFCN methods for change detection of multi-temporal high-resolution remote sensing images based on multi-scale feature convolution units. Wu J et al. [
29] proposed a deep supervised network (DSAHRNet) model. After the network extracts the decoding change information, the features are refined by parallel stacking of convolutional blocks, and more discriminative features can be obtained with the deep supervised module.
The attention mechanism is introduced in change-detection convolutional networks to focus on change information in complex information as well. Chen, J et al. [
30] proposed DASNet, a change-detection model based on the dual attention full convolutional twin neural network, to obtain change-detection results by extracting rich features from dual temporal phase maps. Li et al. [
35] introduced the pyramidal attention layer structure into the full convolutional network framework to further extract multi-scale variation information from the difference-feature maps processed by the original network encoder structure. Song et al. [
36] proposed AGCDetNet by combining a fully convolutional network with an attention mechanism. The network takes into account the joint use of a spatial attention mechanism and channel attention mechanism. The paper verifies that AGCDetNet is able to enhance the discrimination of changing targets and backgrounds while improving the performance of feature representation for changing information. Lv et al. [
37] proposed a hybrid attention semantic segmentation network (HAssNet), which incorporates a spatial attention mechanism and a channel attention mechanism based on a fully convolutional network [
38]. This approach effectively utilizes multi-scale extracted features and global correlation to locate and segment targets in the image.
Nevertheless, most of the work only uses the deep features of CNN to build semantic feature descriptions, which ignores the fine-grained information contained in the shallow features [
39]. Du et al. [
40] designed a bilateral semantic fusion twin network (BSFNet) integrating shallow and deep semantic features in order to better map dual-temporal images to semantic feature domains for comparison, and obtained pixel-level change results with more complete structures. The UNet network [
41] has outstanding performance in the field of semantic segmentation, and has been widely adopted into the field of remote sensing change detection. Zhi, Z et al. [
42] proposed a UNet-based CLNet network with a cross-layer structure to improve the change-detection accuracy by improving the way of contextual information fusion. By incorporating the advantages of dense connections for multi-scale information mining within UNet++, Li et al. [
43] introduced multiple sources of information to supplement the channel information of remote sensing images in their framework. The resulting model exhibits excellent performance across various datasets. Chen et al. [
44] combined the attention mechanism with UNet to design the Siamese_AUNet twin neural network. The model performs well in solving the problems related to weak change detection and noise suppression. Furthermore, for change detection, the conditional random field (CRF) based on probabilistic graphical models (PGM) [
45] and the Markov random field (MRF) [
46] have been introduced. Zhang et al. [
47] used the CRF model to improve the traditional change-detection method. A half-normal CRF (HNCRF) method is proposed to construct the interaction between pixel points in the spatial analysis of difference images, which is effective when the change region is small. Lv et al. [
48] proposed a hybrid conditional random field (HCRF) model that combining traditional random field methods with object-based techniques. The improved model fully exploits the spectral spatial information, thereby enhancing the change-detection performance of high-spatial-resolution remote sensing images, improving the traditional change-detection method with the CRF model. A half-normal CRF (HNCRF) method is proposed to construct the interaction between pixel points in the process of the spatial analysis of difference images, which is effective when the change region is not significant. However, CRF ignores the image–global-distribution relationship. The localization accuracy of the fully connected conditional random field (FCCRF) [
49,
50], coupled with the recognition ability of the deep convolutional neural network shows better boundary localization in the change-detection results. Y. Shang et al. [
51] introduced a novel approach to mitigate the issue of excessive feature smoothing in the fully connected conditional random field (FCCRF) model by incorporating region boundary constraints. This method involves obtaining a complete set of pixels in a multi-temporal image, and calculating the average pixel probability, to enable the refinement and classification of boundary information through the regional potential function. Gong et al. [
52] proposed the patch matching method for fully connected CRF optimization, which combined with the results of semantic segmentation network to detect architectural changes in dual-temporal images. However, the post-processing method based on the front-end output still causes the loss of change-detection information. To address this limitation, Zheng et al. [
53] proposed a new end-to-end deep twin CRFs network (PPNet) for high-resolution remote sensing images. The detection results obtained by PPNet are able to refine the edges of change regions and effectively eliminate noise.
Overall, deep learning has shown promising results in change detection of the remote sensing image, and the proposed models and techniques have significantly improved the accuracy and efficiency of the process. Although the change-detection methods for remote sensing imagery have made significant progress, there are still challenges in detecting the direction of areas of change by analyzing difference images, which can be summarized as follows. Firstly, difference images may cause a semantic collapse phenomenon. The original temporal image, as shown in
Figure 1a,b, contains obvious feature classification information, i.e., semantic information. However, the difference operation, as shown in
Figure 1c,d, can quickly locate the change region, but it also leads to a typical semantic collapse phenomenon where the semantic classification information disappears.
Secondly, the multimodal difference images provide complementary information. As demonstrated in the two modal difference images of the Berne data in
Figure 1c,d, the log-ratio difference image has less interference, but the change information is weak, which results in serious missed alarms. On the other hand, the mean-ratio difference image has prominent change information, but the strong interference leads to high false alarms. Thus, the interference and change performance of the two modal difference images are quite different, and improving the semantic perception of change detection through the complementary information of modal difference images is key to improving the overall performance of change detection.
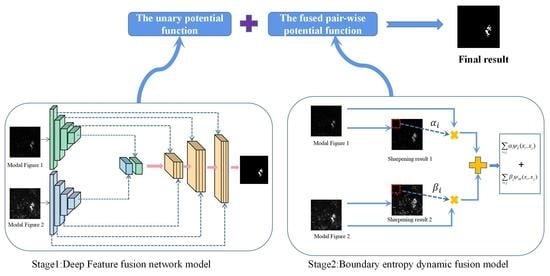
To address the challenges mentioned above, this paper proposes a hierarchical fusion SAR image change-detection method based on hierarchical fusion conditional random field (HF-CRF). The main contributions are as follows.
Designing a dynamic region convolutional semantic segmentation module with a dual encoder–single decoder structure (D-DRUNet). It involves constructing a unary potential function by fusing multimodal difference-image features using neural networks, and enhancing the semantic perception capability of the CRF model.
Introducing a boundary prior to constructing a pair-wise potential function based on multimodal dynamic fusion, and enhancing the boundary perception capability of the CRF model.
This paper consists of the following three parts: the Method section provides a detailed description of the principle and implementation steps of the proposed method; the Experiment section provides the experimental results and analysis; and the Conclusion section summarizes the article.