Tropical Surface Temperature and Atmospheric Latent Heating: A Whole-Tropics Perspective Based on TRMM and ERA5 Datasets

Abstract

Tropical surface temperature (TST) and its connection with atmospheric heating, including tropical latent heating (TLH), is essential to the interannual variability of tropical atmospheric circulation and global teleconnection. Utilizing seasonally averaged satellite-based TRMM precipitation data as a proxy of TLH and ERA5-based TST data from 1998 to 2018, we reveal some new features in terms of cross-hemispheric connection in the TLH and TST variability by decomposing them into equatorially symmetric and antisymmetric components. We find surprisingly that the spatial patterns of TLH projected upon the first principal components (PC1) of symmetric and antisymmetric TSTs over the whole-tropics, are very similar to each other, seemingly at odds with the classic Mastuno–Gill theory. The similarity in the projected TLH patterns is mainly because the PC1s of symmetric and antisymmetric TSTs co-vary temporally with a very high correlation. We use the spatial pattern of local correlation between symmetric and antisymmetric components, for both TST and TLH to depict geographic dependence of the symmetric–antisymmetric connection. We suggest that a whole-tropics perspective, which takes the different but connected nature of equatorially symmetric and antisymmetric modes across the whole-tropics into consideration, may well be useful in understanding and predicting tropical climate variability because clarifying the puzzle raised in this research from such a perspective about the consistency between the observation and the classic Mastuno–Gill theory is directly related to the fundamental dynamics of tropical systems, such as Walker circulation, monsoons, and their relationship with underlying land and sea conditions.

1. Introduction

We define equatorial symmetry, antisymmetry, and asymmetry of any tropical climate variable as the exact same, exact opposite, and different states of that variable at the same latitude in the two hemispheres centered at the Equator. Clearly, any equatorially asymmetric variable can be decomposed as the sum of equatorially symmetric and antisymmetric components of that variable.

Matsuno, in his classic paper, obtained a mathematical solution for the eigenmodes of free tropical waves [1]. Based on their equatorially symmetric or antisymmetric nature, these eigenmodes are associated with totally different spatiotemporal structures of wind and pressure. Gill (1980) presented the spatial structure of stationary, forced tropical atmospheric general circulation in response to thermal forcing, which may be either equatorially symmetric or antisymmetric [2]. For instance, in response to an equatorially symmetric forcing with the maximum located at the Equator, stationary Kevin wave response (Walker-circulation type response) appears at the east side of the forcing, while equatorially symmetric stationary Rossby waves appear at the northwest and southwest sides of the forcing. On the contrary, when the thermal forcing is equatorially antisymmetric, the equatorially antisymmetric stationary mixed Rossby-gravity wave and Rossby wave responses, which may mainly be zonally confined nearby the forcing, lead to a Monsoon-type response with the presence of a cross-equatorial flow and cyclonic response in one hemisphere and anti-cyclonic response in the other hemisphere.

It is well known that tropical sea surface temperature (SST) variability, including the ENSO variability in the Pacific and the modes of SST variability in the tropical Indian Ocean and Atlantic, may affect both the tropical atmospheric and global circulation through atmospheric heating and teleconnections [3,4,5]. Indeed, various meteorological disasters, such as drought, flooding, cold spells, and heat waves, can be associated with the tropical surface temperature forcing in different tropical ocean basins. While many of the studies have been focused on the modes of thermal forcing in individual ocean basins, some studies have considered the cross-basin interaction in the tropics during recent years [6,7].

Given the importance of atmospheric heating in shaping the response of general atmospheric circulation to tropical SST variability, many studies have paid attention to the linkage between SST and tropical atmospheric convection (or tropical latent heating, TLH). While the SST-convection (also TLH or precipitation) linkage can be local, this local connection is highly nonlinear and depends on the large-scale background of tropical circulation [8,9,10,11,12]. On the other hand, the changes in tropical rainfall patterns as responses to modes of tropical SST variability such as ENSO, Indian Ocean Dipole (IOD), and Atlantic Niño are also extensively investigated [6,7].

Due to the hemispheric asymmetry of land–sea distribution, equatorial asymmetry prevails in both the mean climate and the variability of tropical SST and precipitation/ latent heating. Indeed, various mechanisms responsible for the equatorial asymmetry of tropical SST and ITCZ have been proposed, such as the wind–evaporation-feedback mechanism [13], asymmetric upwelling associated with meridional oceanic heat transport [14,15], and coupled atmosphere–ocean energy balance constraint associated with cross-equatorial ocean transport [16], the asymmetric oceanic transport by north equatorial countercurrent (NECC) [17], among others.

It is interesting to note, however, that the decomposition of an asymmetric SST pattern into the sum of equatorial symmetric and antisymmetric components has rarely been conducted, except in an analysis of the interaction of annual-cycle and interannual variability of SST in the tropical Eastern Pacific [18]. The reason is that the hemispheric asymmetry of land–sea distribution makes it impossible to find an SST pair when the underlying boundary is ocean in one hemisphere but is land in the other. However, this difficulty can be easily overcome by using tropical surface temperature, including both SST and land surface temperature, rather than SST only.

Because of the small heat inertia of the land surface, the variability of tropical land surface temperature (LST), in which there are more short time-scale oscillations, is usually considered as a response to SST forcing. While this is physically reasonable, it should be noted that lower frequency variability of LST also exists, and just as SST, LST renders the atmosphere with underlying boundary conditions of momentum, heat, and moisture. Furthermore, the SST-LST asymmetry itself may well lead to an asymmetric response in atmospheric motions. Therefore, we take a different, whole-tropics (30°S–30°N) perspective, which considers tropical SST and LST together, labeled as tropical surface temperature (TST) hereafter.

In this short note, we decompose the TST and TLH into equatorially symmetric and antisymmetric parts and then investigate the relation between the symmetric and antisymmetric components separately for TST and TLH based on correlation analysis. Furthermore, we investigate the relation between interannual TST variability and interannual variability of TLH across the whole-tropics, rather than with the SST confined in a single tropical ocean basin, by applying standard singular value decomposition (SVD), empirical orthogonal function (EOF), correlation, and regression methods.

The layout of the note is as follows. The data and method are presented in Section 2, while Section 3 presents the analysis of the main results. The summary and discussion are in Section 4.

2. Data and Methods

2.1. Data

The Tropical Rainfall Measuring Mission (TRMM) produces tropical and subtropical estimates of precipitation based on remote observations. The TMPA (TRMM Multisatellite Precipitation Analysis) version 7 dataset [19] obtained from the NASA archive (ftp://disc2.nascom.nasa.gov/ftp/data/s4pa//TRMM_L3/, accessed on 24 April 2021) and aggregated to a high spatial (0.25°) and temporal (daily) resolution are employed in this study, with the time domain ranging from 1998 to 2019.

The single-level atmospheric and oceanic variables, named skin temperature and sea surface temperature, are obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5 (ERA5) datasets. These two variables are merged to obtain the TST dataset. They were downloaded with a spatial resolution of 0.25° × 0.25° and monthly temporal resolution from 1998 to 2019 and then interpolated into a resolution of 1.0° × 1.0° using bilinear interpolation for this study.

The Oceanic Niño Index (ONI) is one of the ENSO indices, based on the SST in the Niño 3.4 region, which is obtained from https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni (accessed on 8 November 2022).

2.2. Methods

The variables, for example, the TST or TLH, are divided into two components: equatorially symmetric and antisymmetric. Assuming the TST over the Northern Hemisphere is A, and the TST over the Southern Hemisphere is B with the latitude reversed. The symmetric component is defined as 1/2 (A + B), and the antisymmetric component is 1/2 (A − B) in the Northern Hemisphere and 1/2 (B − A) in the Southern Hemisphere. Therefore, the original field can be divided into the sum of symmetric and antisymmetric fields. Note such a decomposition on the TST, rather than on SST only, can take the intrinsic asymmetry of land–sea contrast into consideration, and hence it may better reveal the coupling of land, sea, and atmosphere over the tropics.

The singular value decomposition analysis (SVD) method of detecting temporally synchronous spatial patterns is also used in this study. The method is based on a singular value decomposition of the matrix whose elements are covariances between observations made at different grid points in two geophysical fields, for example, TST and TLH, in this study. Here, we briefly describe the SVD method following Wallace et al. (1992) [20] and Hu (1997) [21]. TST and TRMM-based TLH data are denoted as $s\left(x,t\right)$ and $z\left(x,t\right)$, respectively, where $x$ is space location, and $t$ is time. The SVD analysis is then a linear transformation:

$$s\left(x,t\right)\approx {\sum }_{n=1}^N{a}_n\left(t\right)p_n\left(x\right)$$

(1)

$$z\left(x,t\right)\approx {\sum }_{n=1}^N{b}_n\left(t\right)q_n\left(x\right)$$

(2)

in which the pairs of coupled spatial patterns, $p_n\left(x\right)$ and $q_n\left(x\right)$ (also called left and right SVD spatial patterns, respectively), and their temporal expansion coefficients, $a_n\left(t\right)$ and $b_n\left(t\right)$, are identified. Here N is the number of SVD modes. As described by Zhang et al. (2018) [22], the SVD analysis was conducted as follows: First, the cross-covariance matrix of $s\left(x,t\right)$ and $z\left(x,t\right)$, $C_{sz}$, was calculated. Secondly, the eigenvalues (also called singular values) ${\sigma }_n$ of the matrix were obtained by solving $\left|C_{sz}-\sigma I\right|=0$ where $I$is the identity matrix. Next, the eigenvectors (that is, the SVD patterns, $p_n\left(x\right)$ and $q_n\left(x\right)$) corresponding to each eigenvalue were obtained. $p_n\left(x\right)$, $q_n\left(x\right)$, $a_n\left(t\right)$, and $b_n\left(t\right)$ are the components of an SVD mode. All modes are arranged so that their ${\sigma }_n$ appear in descending order. The first pair of singular patterns describes the largest fraction of the squire covariance between the two fields, and each succeeding pair describes a maximum fraction of square covariance that is unexplained by the previous pairs. The contribution of the nth mode to the total covariance of the two fields is measured by squared covariance fraction:

$$SC{F}_n={\sigma }_n^2/{\sum }_n^N{\sigma }_n^2$$

(3)

To verify the results obtained from the SVD analysis, we further apply the standard empirical orthogonal function (EOF) decomposition to the symmetric and antisymmetric TST fields and then apply the linear regression method onto the TLH field, i.e., by regressing the monthly TLH field upon the principal components (PCs) of the first EOF (EOF1) of symmetric and antisymmetric TST fields. The independent EOF and regression analyses are necessary to verify the robustness of the conclusion obtained from the SVD analysis.

We also calculate the correlation coefficients between symmetric and antisymmetric components of TST (or TLH) locally at each grid point over the tropics. Understandably when the variable at a given location is equatorially asymmetric, the correlation is positive in one hemisphere and negative in another hemisphere; but when the variable at a given location is mainly equatorially symmetric or antisymmetric, then the correlation is weak because one of the symmetric or antisymmetric components is close to zero in this case. As such, the spatial pattern of the correlation may reveal the meridional structure of the variation of TST or TLH.

Figure 1 summarizes the flowchart of methods adopted in this study.

3. Results

Climatology of Annual TLH, TST, Their Symmetric and Antisymmetric Parts

Figure 2 shows the climatology of the annual means of TLH and TST and their symmetric and antisymmetric parts, respectively. The annual mean TLH in Figure 2a shows a zonal band of TLH maxima located between 20$°$S and 20$°$N over the whole-tropics, with the maxima value reaching over 150 ${\mathrm{W}\mathrm{m}}^{-2}$, corresponding to the ITCZ and SPCZ over the Pacific and the ITCZ over the equatorial Atlantic and the monsoonal rainfall over the vast region from Africa to Asia and the Western Pacific, and the rainfall maxima over the Amazon Basin. The symmetric component of the TLH (Figure 2b) exhibits three centers: the largest is located at the Equatorial Indian Ocean to the Western Pacific Ocean, which corresponds well to the largest warm pool of SST (Figure 2); the second is located over the northern part of South America, which corresponds to a relatively low (land) surface temperature, but is also nearby warm Equatorial Atlantic SST at its east flank; the third and smallest center is located over Equatorial Africa, which again corresponds to a relatively low land surface temperature. The antisymmetric component of the TLH (Figure 2c) reveals that: (1) The positive atmospheric latent heating regions in the Northern Hemisphere are associated with the ITCZ over the Pacific and Atlantic and monsoonal precipitation over Asia and maritime continent; (2) The positive atmospheric latent heating regions in the Southern Hemisphere are associated with the SPCZ over the Pacific and ITCZ over the Indian Ocean, and also the two broad northwest–southeast-oriented regions over Southern Africa to the Western Indian Ocean and over South America to West Atlantic. By comparing the corresponding annual-mean TST pattern (Figure 2d) and its symmetric (Figure 2e) and antisymmetric (Figure 2f) components with the TLH pattern, we find that the high TLH (rainfall) zones over the sea surface correspond to high SST, but the high TLH zones over the land surface are associated with relatively lower LST. Indeed, the high LST regions are usually desert areas with little rainfall, but the low LST regions are usually associated with tropical forests. This asymmetry in the TLH-TST relation between the land and sea surfaces may have important implications for tropical atmospheric dynamics.

To further investigate the relationship between TST and TLH, SVD analysis is employed for the original seasonal TST anomaly and the original seasonal TLH anomaly. Note the anomalies in both fields mean that the mean seasonal cycles of TLH and TST have been removed. It can be observed in Figure 3a,b that the leading SVD mode of the TST and TLH is related to El Niño–Southern Oscillation (ENSO), with anomalously warmer SST over the Equatorial Central and Eastern Pacific, cooler SST over the Western Pacific, and also anomalously warmer SST over the Indian Ocean. Correspondingly, anomalously larger TLH is associated with more precipitation over the Central Pacific (near 180°E) and the Equatorial Indian Ocean; also, equatorially shifted ITCZ and SPCZ are found over the Pacific, while anomalously smaller TLH dominates over the Western Pacific (Figure 3b).

To compare the difference between the symmetric and antisymmetric TSTs’ connection with the original TLH, SVD analyses are also applied to the symmetric and antisymmetric components of TST paired with the original TRMM-based TLH as shown in Figure 3c,d for the first SVD mode of symmetric TST and original TLH, and Figure 3e,f for the first SVD mode of antisymmetric TST and original TLH. We surprisingly find that the first SVD modes of original TLH corresponding to the first SVD modes of symmetric and antisymmetric components of TST show very high similarities (Figure 3d,f), which resemble the pattern in Figure 3b. This seems at odds with the classic Mastuno–Gill theory, which implies a one-to-one correspondence between the (anti) symmetric forcing and (anti)symmetric atmospheric response. To verify the above results, we check the time series of the expansion coefficient of the three left (TST) patterns (Figure 3g) and three right (TLH) patterns (Figure 3h). The high correlation coefficients between each other indicate that the leading symmetric and antisymmetric SVD modes co-vary temporally (

Table 1. The correlation coefficients between the time series of the expansion coefficient of three left and right SVD patterns.

	r	Significance Level
TST vs. TLH (original)	0.9	<0.01
Symmetric TST (TST_SYM) vs. original TLH	0.89	<0.01
Antisymmetric TST (TST_ASYM) vs. original TLH	0.82	<0.01

) and are highly consistent with the evolution of El Niño events in the tropical Pacific (

Table 2. The correlation coefficients between the time series of the expansion coefficient of three left and right SVD patterns and the Oceanic Niño Index.

	r	Significance Level
TST vs. ONI	0.915	<0.01
TLH (TST) vs. ONI	0.933	<0.01
TST_SYM vs. ONI	0.928	<0.01
TLH (TST_SYM) vs. ONI	0.935	<0.01
TST_ASYM vs. ONI	0.763	<0.01
TLH (TST_ASYM) vs. ONI	0.925	<0.01

).

To further prove the results obtained from the SVD analysis, we independently employed the EOF analysis for the original seasonal TST anomaly and its symmetric and antisymmetric components (Figure 4). We find the first EOF (EOF1) mode of the seasonal TST anomaly resembles the first left (TST) SVD model in Figure 3a, both indicating the pattern of El Niño events. Furthermore, the EOF1 mode of the symmetric TST in Figure 4b shows a very high similarity with the EOF1 of the original TST (Figure 4a), with the pattern correlation being 0.99, with a significance level less than 0.01. However, the EOF1 mode of the antisymmetric TST (Figure 4c and

Table 3. The correlation coefficients between the principle components of the EOF1 of TST, TST_SYM, and TST_ASYM.

	r	Significance Level
TST_PC1& TST_SYM_PC1	0.99	<0.01
TST_PC1&TST_ASYM_PC1	0.87	<0.01
TST_SYM_PC1&TST_ASYM_PC1	0.82	<0.01

) indicates there is also a weaker but non-negligible antisymmetric TST component across the whole-tropics. In addition, the correlation between the corresponding principle components (PCs) of the EOF1 of symmetric and antisymmetric TSTs is 0.82 (Figure 4c and Table 3), with a significance level of less than 0.01. In short, it can be concluded that while the principal EOF mode of TST interannual variability is dominated by its equatorially symmetric component, there is a non-negligible equatorially antisymmetric component that well co-varies with the symmetric part over most parts of the tropical land and ocean areas. Figure 4d (see also the correlation coefficients in

Table 4. The correlation coefficients between principle components of the EOF1 of TST, TST_SYM, TST_ASYM, and the Oceanic Niño Index.

	R	Significance Level
TST_PC1& ONI	0.897	<0.01
TST_SYM_PC1&ONI	0.907	<0.01
TST_ASYM_PC1&ONI	0.721	<0.01

) shows that the PC1s of original, symmetric, and antisymmetric TST fields are consistent with the evolution of El Niño conditions in the tropical Pacific.

Then we further reveal the link between the symmetric or antisymmetric components of TST and the TRMM-based TLH by calculating the correlation (Figure 5a,e) and regression (Figure 5b,f) of the TLH with/onto the corresponding PCs of the EOF1 of symmetric and antisymmetric TSTs. The regression patterns of TLH in Figure 5b,f are also further separated into equatorially symmetric and antisymmetric components in Figure 5c,d (regressed onto PC1 of the symmetric TST) and in Figure 5g,h (regressed onto PC1 of antisymmetric TST), respectively. It is obvious that the correlation or regression patterns of the TLH associated with the PC1 of symmetric TST (the left panel of Figure 5) are very similar to that associated with the PC1 of antisymmetric TST (the right panel of Figure 5). As such, we confirm the results obtained from the SVD analysis are right.

To depict the geographic dependence of the symmetric–antisymmetric connection, the local correlations between the symmetric and antisymmetric components of both TST and TLH are calculated in Figure 6a,b. By definition, the high correlation in Figure 6 implies the co-variation between symmetric and antisymmetric components, in which the regions with positive correlation further indicate the dominant regions in the symmetric–antisymmetric connection. Indeed, this corresponds to the condition of equatorially asymmetric variation, i.e., temporal variation is strong in one hemisphere only while very weak in the other hemisphere. On the other hand, low correlations mean that one of the equatorially symmetric and antisymmetric components is dominant, and the symmetric and antisymmetric components vary independently (i.e., being mathematically orthogonal with each other). The low correlation region for TST mainly extends from the Equatorial West Pacific to the Middle Equatorial Pacific (Figure 6a), consistent with the equatorially symmetric SST variability over this region, while the high positive correlations (Figure 6a) in the tropics are located over the Southeastern Pacific, Northern Equatorial Atlantic, North Africa, Australia, South Asia, Southern South America, clearly being consistent with asymmetric TST variability associated with the equatorially asymmetric land–sea distribution. On the other hand, the low correlation regions for TLH (Figure 6b) are mainly limited in the narrow regions of equatorial Africa, the Indian Ocean, western to middle equatorial Pacific, and equatorial South America, but the regions with a high positive correlation of TLH are consistent with the monsoonal rainfall over Africa, Asia, and North America, and also the ITCZs over the Pacific and Atlantic in the Northern Hemisphere, with the SPCZ over the Pacific, ITCZ over the Indian Ocean, and rainfall region over Southern Africa and Southern America in the Southern Hemisphere.

Figure 6 indicates that the symmetric and antisymmetric components of both TST and TLH co-vary over vast regions of the tropics, and hence the corresponding Matsuno–Gill modes are intrinsically coupled with each other in the tropical ocean-atmosphere–land system. Untangling their relationship through model simulations and mechanistic analysis is needed for a better theoretical understanding of tropical dynamics.

4. Summary and Discussion

By utilizing seasonally averaged satellite-based TRMM precipitation data as a proxy of tropical latent heating (TLH) and ERA5-based tropical surface temperature (TST) data from 1998 to 2018, we investigate the cross-hemispheric connection in the TLH and TST variability and their co-variability. The interannual variability of both the TST and the TLH is equatorially asymmetric and can be decomposed as the sum of equatorially symmetric and antisymmetric components. Based on the decomposition, we reveal some new features of variability and co-variability of the TST and TLH. The main results are summarized as follows:

(1)

While the principal mode of TST interannual variability is dominated by its equatorially symmetric component, there is a non-negligible equatorially antisymmetric component that well co-varies with the symmetric part over most parts of the tropical land and ocean areas (Figure 4 and Figure 6a);

(2)

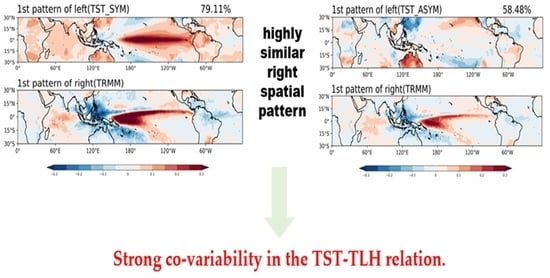
For the principal mode of TLH (and tropical rainfall) interannual variability, we find that equatorial symmetric components dominate only over a zonal band over from the near-Equator Indian Ocean to western and middle equatorial Pacific, salient equatorially antisymmetric variability exists over the middle and Eastern Pacific (Figure 5). In general, the symmetric and antisymmetric TLH exhibits high co-variability over most areas of the tropics (Figure 6b).

(3)

We find surprisingly that the spatial patterns of TLH projected upon the first principal components (PC1) of symmetric and antisymmetric TSTs over the whole-tropics, are very similar to each other, seemingly at odds with the classic Mastuno–Gill theory. The similarity in the projected TLH patterns is mainly due to the fact that the symmetric and antisymmetric PCs of TST are both nearly coincident with the ENSO index during the 21 years of 1998–2018.

While these results are obtained for all four seasons with the mean seasonal cycle being removed, we note they basically hold individually for each season. Results on individual season-based analyses will be reported later in more detail.

The above results raise some interesting puzzles in the theoretical understanding of tropical atmospheric dynamics. First is that if they are really at odds with the classic Matsuno–Gill theory [1,2] or not. We might expect from the linear Matsuno–Gill theory a one-to-one correspondence between equatorially (anti) symmetric TST forcing and equatorially (anti) symmetric TLH pattern, but due to the intrinsic nonlinearity in tropical dynamics, say, related to convective precipitation, the one-to-one correspondence may at least partially be broken up. Because of the strong co-variability in the observed TST-TLH relation, we may not obtain mechanistic understanding directly from statistical analysis of the observations. Well-designed modeling experiments and theoretical analysis are needed for a decisive solution to the puzzle.

The second puzzle is to what extent are the equatorially symmetric and antisymmetric components of the joint TST-TLH variability interactive with each other? What is the underlying mechanism responsible for the interaction? Indeed, it is quite reasonable to assume that the Matsuno–Gill theory still holds to some degree for the interannual joint TST-TLH variability, but the departure from the theory due to nonlinear interactions may be essential to better understand and predict the tropical variability.

While the PCs of joint TST-TLH variability are clearly associated with the ENSO cycle in the tropical Pacific, the co-variability over the Indian Ocean, tropical Atlantic, and tropical land areas should not be neglected from our analysis. Recent studies have suggested the importance of pantropical interaction or cross-basin interaction in tropical dynamics [6,7]. We further suggest that a whole-tropics perspective that takes the different but connected nature of equatorially symmetric and antisymmetric modes across the whole-tropics into consideration may well be useful in understanding and predicting tropical climate variability.

5. Historical Note

After graduating from the University of Chicago with his famous thesis on energy dispersion in the atmosphere, T.C. Yeh stayed there and became a member of the team on tropical dynamics, second to H. Riehl, the head of the team. The other two members were J. Malkus (J. Simpson) and N. LaSeur. Before his return to China, he published two classic papers on the intensity of the Hadley cell [23] and on trade inversion [24], among others. Although later on he did not focus on tropical dynamics in his lifelong career, his works on tropical dynamics also clearly reflect his style and character in research, i.e., being thorough, systematic, and insightful. This short note is devoted to Prof. Yeh’s contribution to the field of tropical dynamics—J. Lu.