Worst-Case Integrity Risk Sensitivity for RAIM with Constellation Modernization
Abstract
:1. Introduction
2. Integrity Risk Estimation for RAIM
- The first group of parameters is the fault-induced bias bi, which is impractical to obtain accurately. However, based on the worst-case protection concept, the effect of the bias on the integrity risk can be strictly determined.
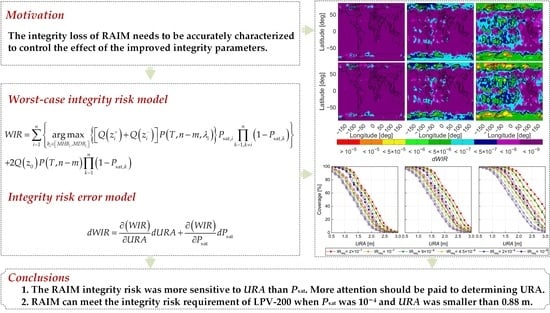
- The second group includes the parameters benefiting from the improvement in the aspects of SIS performance and probability of satellite fault, i.e., URA and Psat. This second group will improve with the constellation modernization. The integrity loss introduced by the improved second group of parameters needs to be strictly characterized, which is the focus of this contribution.
- The third group is determined by the positioning, integrity and continuity requirement, including the alert limit and the probabilities of false alarm (Pfa) and missed detection (Pmd). The third group of parameters is generally constant for the specific required navigation performance (RNP): e.g., the different flight phases in civil aviation defined by the international civil aviation organization (ICAO).
- The fourth group of parameters is the satellite geometry, which has a great impact on integrity performance. The influence of satellite geometry on the integrity performance cannot be neglected.
3. Worst-Case Integrity Risk and Sensitivity Determination
4. Simulation and Analysis
4.1. Impact of URA and Psat
4.2. Acceptable URA and Psat
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Paziewski, J.; Crespi, M. High-precision multi-constellation GNSS: Methods, selected applications and challenges. Meas. Sci. Technol. 2020, 31, 010101. [Google Scholar] [CrossRef]
- Li, L.; Zhao, L.; Yang, F.; Li, N. A novel ARAIM approach in probability domain for combined GPS and Galileo. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Zhu, Y.; Zhang, Q.; Mao, Y.; Cui, X.; Cai, C.; Zhang, R. Comprehensive performance review of BDS-3 after one-year official operation. Adv. Space Res. 2022, 71, 883–899. [Google Scholar] [CrossRef]
- Haddad, R.; Kovach, K.; Slattery, R.; Gillis, J. GPS modernization and beyond. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020. [Google Scholar]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- DoD U.S. Global Positioning System Standard Positioning Service Performance Standard, 4th ed.; 2008; Chapter 3; pp. 21–22. Available online: https://www.gps.gov/technical/ps/2008-SPS-performance-standard.pdf (accessed on 4 June 2023).
- DoD U.S. Global Positioning System Standard Positioning Service Performance Standard, 5th ed.; 2020; Chapter 3; pp. 43–50. Available online: https://www.gps.gov/technical/ps/2020-SPS-performance-standard.pdf (accessed on 4 June 2023).
- Wang, R.; Walter, T. Characterization and Comparison of Galileo and GPS Anomalies. In Proceedings of the 2023 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 25–27 January 2023. [Google Scholar]
- Liu, X.; Wang, R.; Blanch, J.; Walter, T. Evaluation of Satellite Clock and Ephemeris Error Bounding Predictability for Integrity Applications. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022. [Google Scholar]
- Zhao, Y.; Cheng, C.; Li, L.; Wang, R.; Liu, Y.; Li, Z.; Zhao, L. BDS signal-in-space anomaly probability analysis over the last 6 years. GPS Solut. 2021, 25, 49. [Google Scholar] [CrossRef]
- Wang, S.; Zhai, Y.; Zhan, X. Characterizing BDS signal-in-space performance from integrity perspective. Navigation 2021, 68, 157–183. [Google Scholar] [CrossRef]
- Walter, T.; Enge, P. Weighted RAIM for precision approach. In Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION ITM 1995), Palm Springs, CA, USA, 12–15 September 1995. [Google Scholar]
- Li, L.; Wang, H.; Jia, C.; Zhao, L.; Zhao, Y. Integrity and continuity allocation for the RAIM with multiple constellations. GPS Solut. 2017, 21, 1503–1513. [Google Scholar] [CrossRef]
- Chan, F.; Joerger, M.; Khanafseh, S.; Pervan, B. Bayesian fault-tolerant position estimator and integrity risk bound for GNSS navigation. J. Navig. 2014, 67, 753–775. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Shi, H.; Jia, C.; Cheng, J.; Li, H.; Zhao, L. Position-domain integrity risk-based ambiguity validation for the integer bootstrap estimator. GPS Solut. 2018, 22, 39. [Google Scholar] [CrossRef]
- Joerger, M.; Stevanovic, S.; Langel, S.; Pervan, B. Integrity risk minimisation in RAIM part 1: Optimal detector design. J. Navig. 2016, 69, 449–467. [Google Scholar] [CrossRef] [Green Version]
- Blanch, J.; Walter, T. Stress testing advanced RAIM airborne algorithms. In Proceedings of the 2020 International Technical Meeting of The Institute of Navigation (ION ITM 2020), San Diego, CA, USA, 21–24 January 2020. [Google Scholar]
- El-Mowafy, A.; Yang, C. Limited sensitivity analysis of ARAIM availability for LPV-200 over Australia using real data. Adv. Space Res. 2016, 57, 659–670. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; She, J.; Odeh, A.; Bian, B. Horizontal advanced RAIM performance sensitivity to mischaracterizations in integrity support message values. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Lee, Y.; Bian, B.; Odeh, A.; She, J. Sensitivity of advanced RAIM performance to mischaracterizations in integrity support message values. Navigation 2021, 68, 541–558. [Google Scholar] [CrossRef]
- Wang, L.; Luo, S.; Tu, R.; Fan, L.; Zhang, Y. ARAIM with BDS in the Asia-Pacific region. Adv. Space Res. 2018, 62, 707–720. [Google Scholar] [CrossRef]
- Milner, C.; Ochieng, W. Weighted RAIM for APV: The ideal protection level. J. Navig. 2011, 64, 61–73. [Google Scholar] [CrossRef]
- Rife, J.; Phelts, R. Formulation of a time-varying maximum allowable error for ground-based augmentation systems. IEEE Trans. Aerospace Electron. Syst. 2008, 44, 548–560. [Google Scholar] [CrossRef]
- EU-U.S. Cooperation on Satellite Navigation Working Group C. ARAIM Technical Subgroup Milestone 3 Report. February 2016. Available online: https://ec.europa.eu/docsroom/documents/15641/attachments/1/translations/en/renditions/pdf (accessed on 4 June 2023).
- Blanch, J.; Walter, T.; Milner, C.; Joergeret, M.; Pervan, B.; Bouvet, D. Baseline advanced RAIM user algorithm: Proposed updates. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation (ION ITM 2022), Long Beach, CA, USA, 25–27 January 2022. [Google Scholar]
- Working Group C, ARAIM Technical Subgroup. WG-C Advanced RAIM Technical Subgroup Reference Airborne Algorithm Description Document. 20 June 2019. Available online: https://web.stanford.edu/group/scpnt/gpslab/website_files/maast/ARAIM_TSG_Reference_ADD_v3.1.pdf (accessed on 4 June 2023).
- Ma, X.; He, X.; Yu, K.; Montillet, J.; Lu, T.; Yan, L.; Zhao, L. Progress of global ARAIM availability of BDS-2/BDS-3 with TGD and ISB. Adv. Space Res. 2022, 70, 935–946. [Google Scholar] [CrossRef]
- Luo, S.; Wang, L.; Tu, R.; Zhang, W.; Chen, C. Satellite selection methods for multi-constellation advanced RAIM. Adv. Space Res. 2019, 65, 1503–1517. [Google Scholar] [CrossRef]
- RTCA DO-253C. Minimum Operational Performance Standards (MOPS) for GPS Local Area Augmentation System (LAAS) Airborne Equipment; RTCA, Inc.: Washington, DC, USA, 2008; Chapter 2; pp. 58–59. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline advanced RAIM user algorithm and possible improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Multi-GNSS signal-in-space range error assessment-methodology and results. Adv. Space Res. 2018, 61, 3020–3038. [Google Scholar] [CrossRef]
- Wu, W.; Guo, F.; Zheng, J. Analysis of Galileo signal-in-space range error and positioning performance during 2015–2018. Satell. Navig. 2020, 1, 6. [Google Scholar] [CrossRef] [Green Version]
- ICAO, Annex 10. GNSS Standards and Recommended Practices (SARPs), 7th ed.; ICAO: Montreal, QC, Canada, 2018; Chapter 3; pp. 71–72. ISBN 978-92-9258-504-4. [Google Scholar]




| Parameters | Value |
|---|---|
| URA | 1.0/1.5/2.0 m |
| Psat | 10−5/10−4/10−3 |
| Pfa requirement | 10−5 |
| Pmd requirement | 10−3 |
| VAL | 35 m |
| Constellation | GPS + BDS |
| Simulation duration | 10 days |
| Time step | 10 min |
| Cut-off elevation angle | 10 deg |
| Value | Increased by # | Worst-Case Integrity Risk | Coverage (99.5%) | |||||
|---|---|---|---|---|---|---|---|---|
| Average WIR | Maximum WIR | Average dWIR | Maximum dWIR | IRreq = 9 × 10−8 | IRreq = 4.5 × 10−8 | |||
| URA (m) | 1.0 | 15% | 1.37 × 10−8 | 4.65 × 10−6 | 4.20 × 10−9 | 1.43 × 10−6 | 98.17% | 97.41% |
| 30% | 3.14 × 10−8 | 8.14 × 10−6 | 8.70 × 10−9 | 2.96 × 10−6 | 96.23% | 94.82% | ||
| 1.5 | 15% | 2.92 × 10−7 | 2.57 × 10−5 | 9.62 × 10−8 | 8.11 × 10−6 | 73.55% | 69.22% | |
| 30% | 7.23 × 10−7 | 3.57 × 10−5 | 1.97 × 10−7 | 1.67 × 10−5 | 63.01% | 57.61% | ||
| 2.0 | 15% | 2.24 × 10−6 | 5.07 × 10−5 | 8.54 × 10−7 | 1.53 × 10−5 | 41.51% | 34.74% | |
| 30% | 4.84 × 10−6 | 7.57 × 10−5 | 1.73 × 10−6 | 3.12 × 10−5 | 19.71% | 12.60% | ||
| Psat | 10−5 | 15% | 1.07 × 10−8 | 1.82 × 10−6 | 9.60 × 10−9 | 8.12 × 10−7 | 97.79% | 96.00% |
| 30% | 1.21 × 10−8 | 2.05 × 10−6 | 1.97 × 10−8 | 1.67 × 10−6 | 97.34% | 95.78% | ||
| 10−4 | 15% | 1.07 × 10−7 | 1.82 × 10−5 | 1.22 × 10−8 | 2.25 × 10−6 | 90.45% | 85.65% | |
| 30% | 1.21 × 10−7 | 2.05 × 10−5 | 2.43 × 10−8 | 4.50 × 10−6 | 89.80% | 84.67% | ||
| 10−3 | 15% | 1.05 × 10−6 | 1.79 × 10−4 | 9.51 × 10−7 | 8.03 × 10−5 | 72.91% | 69.56% | |
| 30% | 1.19 × 10−6 | 2.02 × 10−4 | 1.95 × 10−6 | 1.65 × 10−4 | 72.26% | 68.91% | ||
| Psat | Constellation | Coverage | Integrity Risk Requirement | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 × 10−7 | 10−7 | 9 × 10−8 | 4.5 × 10−8 | 2 × 10−8 | 10−8 | ||||
| URA (m) | 10−5 | 24 GPS + 27 BDS | 99.5% | 1.36 | 1.26 | 1.24 | 1.14 | 1.04 | 0.98 |
| 95.0% | 1.84 | 1.70 | 1.68 | 1.58 | 1.46 | 1.38 | |||
| 23 GPS + 26 BDS | 99.5% | 0.84 | 0.70 | 0.68 | 0.56 | / | / | ||
| 95.0% | 1.32 | 1.20 | 1.18 | 1.08 | 0.96 | 0.88 | |||
| 10−4 | 24 GPS + 27 BDS | 99.5% | 1.04 | 0.98 | 0.96 | 0.88 | 0.80 | 0.72 | |
| 95.0% | 1.46 | 1.38 | 1.36 | 1.28 | 1.20 | 1.14 | |||
| 23 GPS + 26 BDS | 99.5% | / | / | / | / | / | / | ||
| 95.0% | 0.96 | 0.88 | 0.86 | 0.78 | 0.68 | 0.60 | |||
| 10−3 | 24 GPS + 27 BDS | 99.5% | 0.80 | 0.72 | 0.72 | 0.66 | 0.56 | / | |
| 95.0% | 1.20 | 1.14 | 1.14 | 1.08 | 1.00 | 0.96 | |||
| 23 GPS + 26 BDS | 99.5% | / | / | / | / | / | / | ||
| 95.0% | 0.68 | 0.60 | 0.58 | 0.52 | / | / | |||
| Third Group of Parameters | Coverage | Integrity Risk Requirement | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 × 10−7 | 10−7 | 9 × 10−8 | 4.5 × 10−8 | 2 × 10−8 | 10−8 | ||||
| URA (m) | Pfa | 8 × 10−6 | 99.5% | 1.04 | 0.96 | 0.94 | 0.88 | 0.78 | 0.70 |
| 95.0% | 1.44 | 1.36 | 1.34 | 1.26 | 1.20 | 1.14 | |||
| 4 × 10−6 | 99.5% | 1.00 | 0.92 | 0.92 | 0.82 | 0.74 | 0.68 | ||
| 95.0% | 1.40 | 1.32 | 1.30 | 1.24 | 1.16 | 1.10 | |||
| Pmd | 10−4 | 99.5% | 1.04 | 0.98 | 0.96 | 0.90 | 0.80 | 0.72 | |
| 95.0% | 1.46 | 1.38 | 1.36 | 1.28 | 1.20 | 1.14 | |||
| 10−5 | 99.5% | 1.04 | 0.98 | 0.96 | 0.90 | 0.80 | 0.72 | ||
| 95.0% | 1.46 | 1.38 | 1.36 | 1.28 | 1.20 | 1.14 | |||
| VAL (m) | 20 | 99.5% | / | / | / | / | / | / | |
| 95.0% | / | / | / | / | / | / | |||
| 30 | 99.5% | 0.64 | 0.50 | / | / | / | / | ||
| 95.0% | 1.08 | 0.98 | 0.98 | 0.90 | 0.80 | 0.74 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, L.; Li, R.; Li, M.; Cheng, L. Worst-Case Integrity Risk Sensitivity for RAIM with Constellation Modernization. Remote Sens. 2023, 15, 2979. https://doi.org/10.3390/rs15122979
Wang L, Li L, Li R, Li M, Cheng L. Worst-Case Integrity Risk Sensitivity for RAIM with Constellation Modernization. Remote Sensing. 2023; 15(12):2979. https://doi.org/10.3390/rs15122979
Chicago/Turabian StyleWang, Liuqi, Liang Li, Ruijie Li, Min Li, and Li Cheng. 2023. "Worst-Case Integrity Risk Sensitivity for RAIM with Constellation Modernization" Remote Sensing 15, no. 12: 2979. https://doi.org/10.3390/rs15122979
APA StyleWang, L., Li, L., Li, R., Li, M., & Cheng, L. (2023). Worst-Case Integrity Risk Sensitivity for RAIM with Constellation Modernization. Remote Sensing, 15(12), 2979. https://doi.org/10.3390/rs15122979